Hostname: page-component-7dd5485656-frp75 Total loading time: 0 Render date: 2025-10-29T09:27:14.791Z Has data issue: false hasContentIssue false
  • English
  • Français

Distribution of shapes of orthogonal lattices

Published online by Cambridge University Press:  02 November 2017

MANFRED EINSIEDLER ,
RENÉ RÜHR Open the ORCID record for RENÉ RÜHR [Opens in a new window]  and
PHILIPP WIRTH
MANFRED EINSIEDLER
Affiliation:
D-Math, ETH Zürich, Rämistrasse 101, CH-8092 Zürich, Switzerland email manfred.einsiedler@math.ethz.ch, philipp.wirth@math.ethz.ch
RENÉ RÜHR
Affiliation:
Department of Mathematics, University of Tel Aviv, 69978 Tel-Aviv, Israel email reneruehr@gmail.com
PHILIPP WIRTH
Affiliation:
D-Math, ETH Zürich, Rämistrasse 101, CH-8092 Zürich, Switzerland email manfred.einsiedler@math.ethz.ch, philipp.wirth@math.ethz.ch
Get access Rights & Permissions [Opens in a new window]

Abstract

It was recently shown by Aka, Einsiedler and Shapira that if 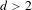$d>2$, the set of primitive vectors on large spheres when projected to the 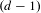$(d-1)$-dimensional sphere coupled with the shape of the lattice in their orthogonal complement equidistribute in the product space of the sphere with the space of shapes of 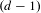$(d-1)$-dimensional lattices. Specifically, for 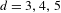$d=3,4,5$ some congruence conditions are assumed. By using recent advances in the theory of unipotent flows, we effectivize the dynamical proof to remove those conditions for 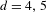$d=4,5$. It also follows that equidistribution takes place with a polynomial error term with respect to the length of the primitive points.

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 6 , June 2019 , pp. 1531 - 1607
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aka, M., Einsiedler, M. and Shapira, U.. Integer points on spheres and their orthogonal grids. J. Lond. Math. Soc. (2) 93(1) (2016), 143–158.Google Scholar
Aka, M., Einsiedler, M. and Shapira, U.. Integer points on spheres and their orthogonal lattices. Invent. Math. 206(2) (2016), 379–396.Google Scholar
Borel, A. and Prasad, G.. Finiteness theorems for discrete subgroups of bounded covolume in semi-simple groups. Publ. Math. Inst. Hautes Études Sci. 69 (1989), 119–171.Google Scholar
Dani, S. and Margulis, G.. Asymptotic behaviour of trajectories of unipotent flows on homogeneous spaces. Proc. Indian Acad. Sci. Math. Sci. 101(1) (1991), 1–17.Google Scholar
Duke, W.. Hyperbolic distribution problems and half-integral weight Maass forms. Invent. Math. 92(1) (1988), 73–90.Google Scholar
Einsiedler, M., Margulis, G., Mohammadi, A. and Venkatesh, A.. Effective equidistribution and property (tau). Preprint, 2015 arXiv:1503.05884, submitted.Google Scholar
Einsiedler, M., Mozes, S., Shah, N. and Shapira, U.. Equidistribution of primitive rational points on expanding horospheres. Compos. Math. 152(4) (2015), 667–692.Google Scholar
Einsiedler, M., Margulis, G. and Venkatesh, A.. Effective equidistribution for closed orbits of semisimple groups on homogeneous spaces. Invent. Math. 177(1) (2009), 137–212.Google Scholar
Ellenberg, J. S. and Venkatesh, A.. Local–global principles for representations of quadratic forms. Invent. Math. 171(2) (2008), 257–279.Google Scholar
Gorodnik, A., Maucourant, F. and Oh, H.. Manin’s and Peyre’s conjectures on rational points and adelic mixing. Ann. Sci. Éc. Norm. Supér. (4) 41(3) (2008), 383–435.Google Scholar
Gorodnik, A. and Oh, H.. Rational points on homogeneous varieties and equidistribution of adelic periods. Geom. Funct. Anal. 21(2) (2011), 319–392. With an appendix by Mikhail Borovoi.Google Scholar
Hilbert, D.. Beweis für die Darstellbarkeit der ganzen Zahlen durch eine feste Anzahl n ter Potenzen (Waringsches Problem). Math. Ann. 67(3) (1909), 281–300.Google Scholar
Iwaniec, H.. Fourier coefficients of modular forms of half-integral weight. Invent. Math. 87(2) (1987), 385–401.Google Scholar
Kleinbock, D. Y. and Margulis, G. A.. Flows on homogeneous spaces and Diophantine approximation on manifolds. Ann. of Math. (2) 148(1) (1998), 339–360.Google Scholar
Kleinbock, D. and Tomanov, G.. Flows on S-arithmetic homogeneous spaces and applications to metric Diophantine approximation. Comment. Math. Helv. 82(3) (2007), 519–581.Google Scholar
Maass, H.. Spherical functions and quadratic forms. J. Indian Math. Soc. (N.S.) 20 (1956), 117–162.Google Scholar
Maass, H.. Über die Verteilung der zweidimensionalen Untergitter in einem euklidischen Gitter. Math. Ann. 137 (1959), 319–327.Google Scholar
Marklof, J.. The asymptotic distribution of Frobenius numbers. Invent. Math. 181(1) (2010), 179–207.Google Scholar
Margulis, G. A.. Discrete Subgroups of Semisimple Lie Groups (Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 17) . Springer, Berlin, 1991.Google Scholar
Mozes, S. and Shah, N.. On the space of ergodic invariant measures of unipotent flows. Ergod. Th. & Dynam. Sys. 15(1) (1995), 149–159.Google Scholar
Margulis, G. A. and Tomanov, G. M.. Invariant measures for actions of unipotent groups over local fields on homogeneous spaces. Invent. Math. 116(1–3) (1994), 347–392.Google Scholar
Oh, H.. Uniform pointwise bounds for matrix coefficients of unitary representations and applications to Kazhdan constants. Duke Math. J. 113(1) (2002), 133–192.Google Scholar
Platonov, V. and Rapinchuk, A.. Algebraic Groups and Number Theory (Pure and Applied Mathematics, 139) . Academic Press, Boston, MA, 1994. Translated from the 1991 Russian original by Rachel Rowen.Google Scholar
Prasad, G.. Volumes of S-arithmetic quotients of semi-simple groups. Publ. Math. Inst. Hautes Études Sci. 69 (1989), 91–117. With an appendix by Moshe Jarden and the author.Google Scholar
Ratner, M.. On the p-adic and S-arithmetic generalizations of Raghunathan’s conjectures. Lie Groups and Ergodic Theory (Mumbai, 1996) (Tata Institute of Fundamental Research Studies in Mathematics, 14) . Tata Institute of Fundamental Research, Bombay, 1998, pp. 167–202.Google Scholar
Schmidt, W. M.. The distribution of sublattices of Z m . Monatsh. Math. 125(1) (1998), 37–81.Google Scholar
Serre, J. P.. A Course in Arithmetic (Graduate Texts in Mathematics, 7) . Springer, New York, 1973, viii+115 pp.Google Scholar
Venkatesh, A.. Sparse equidistribution problems, period bounds and subconvexity. Ann. of Math. (2) 172(2) (2010), 989–1094.Google Scholar