Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-10T11:11:04.908Z Has data issue: false hasContentIssue false
  • English
  • Français

Zero sets of Lie algebras of analytic vector fields on real and complex two-dimensional manifolds

Published online by Cambridge University Press:  07 September 2017

MORRIS W. HIRSCH  and
F.-J. TURIEL
MORRIS W. HIRSCH
Affiliation:
Department of Mathematics, University of Wisconsin at Madison, USA email mwhirsch@chorus.net Department of Mathematics, University of California at Berkeley, USA
F.-J. TURIEL
Affiliation:
Department of Geometry and Topology, University of Malaga, Spain email turiel@agt.cie.uma.es
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $M$ be an analytic connected 2-manifold with empty boundary, over the ground field $\mathbb{F}=\mathbb{R}$ or $\mathbb{C}$. Let $Y$ and $X$ denote differentiable vector fields on $M$. We say that $Y$ tracks 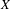$X$ if $[Y,X]=fX$ for some continuous function $f:\,M\rightarrow \mathbb{F}$. A subset $K$ of the zero set $\mathsf{Z}(X)$ is an essential block for $X$ if it is non-empty, compact and open in $\mathsf{Z}(X)$, and the Poincaré–Hopf index $\mathsf{i}_{K}(X)$ is non-zero. Let ${\mathcal{G}}$ be a finite-dimensional Lie algebra of analytic vector fields that tracks a non-trivial analytic vector field $X$. Let $K\subset \mathsf{Z}(X)$ be an essential block. Assume that if $M$ is complex and $\mathsf{i}_{K}(X)$ is a positive even integer, no quotient of ${\mathcal{G}}$ is isomorphic to $\mathfrak{s}\mathfrak{l}(2,\mathbb{C})$. Then ${\mathcal{G}}$ has a zero in $K$ (main result). As a consequence, if $X$ and $Y$ are analytic, $X$ is non-trivial, and $Y$ tracks $X$, then every essential component of $\mathsf{Z}(X)$ meets $\mathsf{Z}(Y)$. Fixed-point theorems for certain types of transformation groups are proved. Several illustrative examples are given.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 4 , April 2019 , pp. 954 - 979
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Belliart, M.. Actions sans points fixes sur les surfaces compactes. Math. Z. 225 (1997), 453–465.Google Scholar
Bonatti, C.. Difféomorphismes commutants des surfaces et stabilité des fibrations en tores. Topology 29 (1990), 101–126.Google Scholar
Bonatti, C.. Champs de vecteurs analytiques commutants, en dimension 3 ou 4: existence de zéros communs. Bol. Soc. Brasil. Mat. (N.S.) 22 (1992), 215–247.Google Scholar
Bonatti, C. and Santiago, B.. Existence of common zeros for commuting vector fields on 3-manifolds. Ann. Inst. Fourier, to appear. Preprint, 2015, arXiv:1504.06104.Google Scholar
Borel, A.. Groupes linéaires algebriques. Ann. of Math. (2) 64 (1956), 20–80.Google Scholar
Cervau, D. and Mattei, J. F.. Formes Intégrales Holomorphes Singulières (Astérisque, 97) . Société Mathématique de France, Paris, 1982.Google Scholar
Dold, A.. Lectures on Algebraic Topology (Grundlehren der mathematischen Wissenschaften, 52) , 2nd edn. Springer, New York, 1972.Google Scholar
Gottlieb, D.. A de Moivre like formula for fixed point theory. Fixed Point Theory and its Applications (Berkeley, CA, 1986) (Contemporary Mathematics, 72) . American Mathematical Society, Providence, RI, 1988.Google Scholar
Griffiths, P. and Harris, J.. Principles of Algebraic Geometry. John Wiley, New York, 1978.Google Scholar
Hirsch, M.. Actions of Lie groups and Lie algebras on manifolds. A Celebration of the Mathematical Legacy of Raoul Bott (Centre de Recherches Mathématiques, Université de Montréal, Proceedings and Lecture Notes, 50) . Ed. Kotiuga, P. R.. American Mathematical Society, Providence, RI, 2010.Google Scholar
Hirsch, M.. Smooth actions of Lie groups and Lie algebras on manifolds. J. Fixed Point Theory Appl. 10(2) (2011), 219–232.Google Scholar
Hirsch, M.. Fixed points of local actions of nilpotent Lie groups on surfaces. Ergod. Th. & Dynam. Sys. 37 (2017), 1238–1252.Google Scholar
Hirsch, M.. Fixed points of local actions of Lie groups on real and complex 2-manifolds. Axioms 4(3) (2015), 313–320. Special issue: Topological Groups: Yesterday, Today, Tomorrow. Published online 27 July 2015.Google Scholar
Hirsch, M.. Common zeros of families of smooth vector fields on surfaces. Preprint, 2015, arXiv:1506.02185.Google Scholar
Hirsch, M.. Zero sets of Lie algebras of analytic vector fields on real and complex 2-dimensional manifolds. Preprint, 2013, arXiv:1310.0081v2.Google Scholar
Hirsch, M. and Turiel, F.-J.. Zero sets of Lie algebras of analytic vector fields on real and complex 2-dimensional manifolds, II. Preprint, 2016, arXiv:1606.08322v1.Google Scholar
Hirsch, M. and Weinstein, A.. Fixed points of analytic actions of supersoluble Lie groups on compact surfaces. Ergod. Th. & Dynam. Sys. 21 (2001), 1783–1787.Google Scholar
Hopf, H.. Vektorfelder in Mannigfaltigkeiten. Math. Ann. 95 (1925), 340–367.Google Scholar
Humphreys, J.. Linear Algebraic Groups. Springer, New York, 1975.Google Scholar
Jacobson, N.. Lie Algebras. Interscience, New York, 1962, reprinted by Dover, New York, 1979.Google Scholar
Jubin, B.. A generalized Poincaré–Hopf index theorem. Preprint, 2009, arXiv:0903.0697.Google Scholar
Lefschetz, S.. On the fixed point formula. Ann. of Math. (2) 38 (1937), 819–822.Google Scholar
Lie, S.. Gruppenregister. Gesammelte Abhandlungen. Vol. 5. Teubner, Leipzig, 1924, pp. 767–773.Google Scholar
Lima, E.. Common singularities of commuting vector fields on 2-manifolds. Comment. Math. Helv. 39 (1964), 97–110.Google Scholar
Molino, P.. Review of Bonatti [ 3 ], Math Reviews 93h:57044. American Mathematical Society, Providence, RI, 1993.Google Scholar
Molino, P. and Turiel, F.-J.. Une observation sur les actions de ℝ n sur les variétés compactes de caractéristique non nulle. Comment. Math. Helv. 61 (1986), 370–375.Google Scholar
Molino, P. and Turiel, F.-J.. Dimension des orbites d’une action de ℝ p sur une variété compacte. Comment. Math. Helv. 63 (1988), 253–258.Google Scholar
Morse, M.. Singular points of vector fields under general boundary conditions. Amer. J. Math. 52 (1929), 165–178.Google Scholar
Palais, R. S.. A global formulation of the Lie theory of transformation groups. Mem. Amer. Math. Soc. 22 (1957), 1–123.Google Scholar
Plante, J.. Fixed points of Lie group actions on surfaces. Ergod. Th. & Dynam. Sys. 6 (1986), 149–161.Google Scholar
Poincaré, H.. Sur les courbes définies par une équation différentielle. J. Math. Pures Appl. 1 (1885), 167–244.Google Scholar
Pugh, C.. A generalized Poincaré index formula. Topology 7 (1968), 217–226.Google Scholar
Schneider, C.. SL(2, R) actions on surfaces. Amer. J. Math. 96 (1974), 511–528.Google Scholar
Smale, S.. Diffeomorphisms of the 2-sphere. Proc. Amer. Math. Soc. 10 (1959), 621–626.Google Scholar
Sommese, A.. Borel’s fixed point theorem for Kaehler manifolds and an application. Proc. Amer. Math. Soc. 41 (1973), 51–54.Google Scholar
Stowe, D.. The stationary set of a group action. Proc. Amer. Math. Soc. 79 (1980), 139–146.Google Scholar
Turiel, F.-J.. Dimension minimale des orbites d’une action symplectique de ℝ n . Lecture Notes in Math. 1416 (1990), 268–289.Google Scholar
Turiel, F.-J.. Analytic actions on compact surfaces and fixed points. Manuscripta Math. 110 (2003), 195–201.Google Scholar
Turiel, F.-J.. Smooth actions of $Aff^{+}(\mathbb{R})$ on compact surfaces with no fixed point: an elementary construction. Preprint, 2016, arXiv:1602.05736.Google Scholar