Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-02-09T01:43:37.461Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodic averages with prime divisor weights in 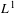$L^{1}$

Published online by Cambridge University Press:  18 August 2017

ZOLTÁN BUCZOLICH Open the ORCID record for ZOLTÁN BUCZOLICH [Opens in a new window]
ZOLTÁN BUCZOLICH*
Affiliation:
Department of Analysis, ELTE Eötvös Loránd University, Pázmány Péter Sétány 1/c, 1117 Budapest, Hungary email buczo@cs.elte.hu
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that 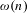$\unicode[STIX]{x1D714}(n)$ and 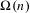$\unicode[STIX]{x1D6FA}(n)$, the number of distinct prime factors of $n$ and the number of distinct prime factors of $n$ counted according to multiplicity, are good weighting functions for the pointwise ergodic theorem in 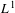$L^{1}$. That is, if $g$ denotes one of these functions and 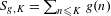$S_{g,K}=\sum _{n\leq K}g(n)$, then for every ergodic dynamical system 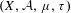$(X,{\mathcal{A}},\unicode[STIX]{x1D707},\unicode[STIX]{x1D70F})$ and every 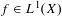$f\in L^{1}(X)$,

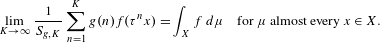$$\begin{eqnarray}\lim _{K\rightarrow \infty }\frac{1}{S_{g,K}}\mathop{\sum }_{n=1}^{K}g(n)f(\unicode[STIX]{x1D70F}^{n}x)=\int _{X}f\,d\unicode[STIX]{x1D707}\quad \text{for }\unicode[STIX]{x1D707}\text{ almost every }x\in X.\end{eqnarray}$$
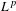This answers a question raised by Cuny and Weber, who showed this result for $L^{p}$, 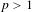$p>1$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 4 , April 2019 , pp. 889 - 897
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cuny, C. and Weber, M.. Ergodic theorems with arithmetical weights. Israel J. Math. 217 (2017), 139–180.Google Scholar
Delange, H.. Sur des formules de Atle Selberg. Acta Arith. 19 (1971), 105–146.Google Scholar
El Abdalaoui, E. H., Kułaga-Przymus, J., Lemańczyk, M. and De La Rue, T.. The Chowla and the Sarnak conjectures from ergodic theory point of view. Discrete Contin. Dyn. Syst. 37(6) (2017), 2899–2944.Google Scholar
Halász, G.. On the distribution of additive and the mean values of multiplicative arithmetic functions. Studia Sci. Math. Hungar. 6 (1971), 211–233.Google Scholar
Hardy, G. H. and Wright, E. M.. An Introduction to the Theory of Numbers, 6th edn. Oxford University Press, Oxford, 2008.Google Scholar
Norton, K. K.. On the number of restricted prime factors of an integer. I. Illinois J. Math. 20(4) (1976), 681–705.Google Scholar
Petersen, K.. Ergodic Theory (Cambridge Studies in Advanced Mathematics, 2) . Cambridge University Press, Cambridge, 1983.Google Scholar
Rosenblatt, J. M. and Wierdl, M.. Pointwise ergodic theorems via harmonic analysis. Ergodic Theory and its Connections with Harmonic Analysis (Alexandria, 1993) (London Mathematical Society Lecture Note Series, 205) . Cambridge University Press, Cambridge, 1995, pp. 3–151.Google Scholar