No CrossRef data available.
Article contents
NONPARAMETRIC IDENTIFICATION AND ESTIMATION OF A GENERALIZED ADDITIVE MODEL WITH A FLEXIBLE ADDITIVE STRUCTURE AND UNKNOWN LINK
Published online by Cambridge University Press: 04 December 2024
Abstract
This paper proposes a nonparametric approach to identify and estimate the generalized additive model with a flexible additive structure and with possibly discrete variables when the link function is unknown. Our approach allows for a flexible additive structure which provides applied researchers the flexibility to specify their model according to economic theory or practical experience. Motivated by the concerns from empirical research, our method also allows for multiple discrete variables in the covariates. By transforming our model into a generalized additive model with univariate component functions, our identification and estimation thereby follows a procedure adapted from the case with univariate components. The estimators converge to normal distributions in large sample with a one-dimensional convergence rate for the link function and a 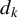 $d_k$-dimensional convergence rate for the component function
$d_k$-dimensional convergence rate for the component function 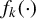 $f_k(\cdot )$ defined on
$f_k(\cdot )$ defined on 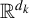 ${\mathbb R}^{d_k}$ for all k.
${\mathbb R}^{d_k}$ for all k.
Information
- Type
- ARTICLES
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
Footnotes
We thank the Co-Editor (Liangjun Su) and three anonymous referees for comments that have greatly improved the article. We also thank the Editor (Peter C.B. Phillips) for his help on improving the presentation of this article. We are very grateful to Chunrong Ai, Xiaohong Chen, Yanqin Fan, LungFei Lee, and Arthur Lewbel for their constructive comments and suggestions. We are also grateful to Liang Chen, Timothy Christensen, Qingfeng Liu, Ryo Okui, Quang Vuong, Hanghui Zhang, Xinyu Zhang, and seminar/conference participants at HKUST, SUFE, Xiamen University, 2019 Asian Meeting of Econometric Society, 2019 China Meeting of Econometric Society, and 2019 Young Econometrician Asia Pacific (YEAP) for helpful comments. The usual disclaimer applies. Liu acknowledges support from the National Natural Science Foundation of China (Grant No. 72394392). Zhou acknowledges support from the National Natural Science Foundation of China (Grant Nos. 72342034 and 72173083). Zequn Jin provided capable research assistance.

