Article contents
Unitary cycles on Shimura curves and the Shimura lift II
Published online by Cambridge University Press: 15 September 2014
Abstract
We consider two families of arithmetic divisors defined on integral models of Shimura curves. The first was studied by Kudla, Rapoport and Yang, who proved that if one assembles these divisors in a formal generating series, one obtains the 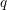 $q$-expansion of a modular form of weight 3/2. The present work concerns the Shimura lift of this modular form: we identify the Shimura lift with a generating series comprising divisors arising in the recent work of Kudla and Rapoport regarding cycles on Shimura varieties of unitary type. In the prequel to this paper, the author considered the geometry of the two families of cycles. These results are combined with the Archimedean calculations found in this work in order to establish the theorem. In particular, we obtain new examples of modular generating series whose coefficients lie in arithmetic Chow groups of Shimura varieties.
$q$-expansion of a modular form of weight 3/2. The present work concerns the Shimura lift of this modular form: we identify the Shimura lift with a generating series comprising divisors arising in the recent work of Kudla and Rapoport regarding cycles on Shimura varieties of unitary type. In the prequel to this paper, the author considered the geometry of the two families of cycles. These results are combined with the Archimedean calculations found in this work in order to establish the theorem. In particular, we obtain new examples of modular generating series whose coefficients lie in arithmetic Chow groups of Shimura varieties.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2014
References
- 1
- Cited by

