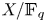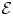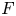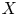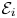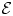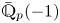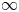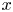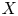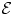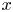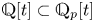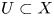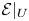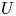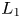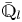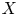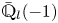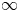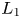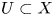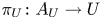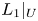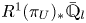1. Introduction
Throughout this paper, ![]() $p$ is a prime number and
$p$ is a prime number and ![]() $q$ is a power of
$q$ is a power of ![]() $p$. If
$p$. If ![]() $X/k$ is a smooth scheme over a perfect field of characteristic
$X/k$ is a smooth scheme over a perfect field of characteristic ![]() $p$, then
$p$, then ![]() $\textbf {F-Isoc}^{{\dagger} }({X})$ denotes the category of overconvergent
$\textbf {F-Isoc}^{{\dagger} }({X})$ denotes the category of overconvergent ![]() $F$-isocrystals on
$F$-isocrystals on ![]() $X$ and
$X$ and ![]() $\textbf {F-Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$ denotes its
$\textbf {F-Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$ denotes its ![]() $\overline {\mathbb {Q}}_p$-linearization. Overconvergent
$\overline {\mathbb {Q}}_p$-linearization. Overconvergent ![]() $F$-isocrystals are a
$F$-isocrystals are a ![]() $p$-adic analog of lisse
$p$-adic analog of lisse ![]() $l$-adic sheaves.
$l$-adic sheaves.
Definition 1.1 Let ![]() $X/k$ be a smooth, geometrically connected scheme over a perfect field
$X/k$ be a smooth, geometrically connected scheme over a perfect field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$ and let
$p$ and let ![]() ${{\mathcal {E}}}\in \textbf {F-Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$. We say that
${{\mathcal {E}}}\in \textbf {F-Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$. We say that ![]() ${{\mathcal {E}}}$ has infinite local monodromy at infinity if, for every triple
${{\mathcal {E}}}$ has infinite local monodromy at infinity if, for every triple ![]() $(X',\overline {X'},f)$ where
$(X',\overline {X'},f)$ where ![]() $\overline {X'}$ is smooth projective over
$\overline {X'}$ is smooth projective over ![]() $k$,
$k$, ![]() $X'\subset \overline {X'}$ is a dense Zariski open subset, and
$X'\subset \overline {X'}$ is a dense Zariski open subset, and ![]() $f\colon X'\rightarrow X$ is an alteration, the overconvergent
$f\colon X'\rightarrow X$ is an alteration, the overconvergent ![]() $F$-isocrystal
$F$-isocrystal ![]() $f^{*}{{\mathcal {E}}}$ does not extend to an
$f^{*}{{\mathcal {E}}}$ does not extend to an ![]() $F$-isocrystal on
$F$-isocrystal on ![]() $\overline {X'}$.
$\overline {X'}$.
This definition of infinite local monodromy at infinity applies equally well to lisse ![]() $\overline {\mathbb {Q}}_l$-sheaves and is compatible with the other notions of infinite local monodromy at infinity.
$\overline {\mathbb {Q}}_l$-sheaves and is compatible with the other notions of infinite local monodromy at infinity.
Theorem 1.2 Let ![]() $X/\mathbb {F}_q$ be a smooth, geometrically connected, quasi-projective scheme. Let
$X/\mathbb {F}_q$ be a smooth, geometrically connected, quasi-projective scheme. Let ![]() ${{\mathcal {E}}}\in \mathbf{F\text{-}Isoc}^{{\dagger} }({X})$ be a semi-simple overconvergent
${{\mathcal {E}}}\in \mathbf{F\text{-}Isoc}^{{\dagger} }({X})$ be a semi-simple overconvergent ![]() $F$-isocrystal. Suppose:
$F$-isocrystal. Suppose:
• for every closed point
 $x$ of
$x$ of  $X$, the polynomial
$X$, the polynomial  $P_x({{\mathcal {E}}},t)$ has coefficients in
$P_x({{\mathcal {E}}},t)$ has coefficients in  ${{\mathbb {Q}}}\subset \mathbb {Q}_p$;
${{\mathbb {Q}}}\subset \mathbb {Q}_p$;• every irreducible summand
 ${{\mathcal {E}}}_i\in \mathbf {F\text{-}Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$ of
${{\mathcal {E}}}_i\in \mathbf {F\text{-}Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$ of  ${{\mathcal {E}}}$ has rank
${{\mathcal {E}}}$ has rank  $2$, determinant
$2$, determinant  $\overline {\mathbb {Q}}_p(-1)$, and infinite local monodromy around infinity.
$\overline {\mathbb {Q}}_p(-1)$, and infinite local monodromy around infinity.
Then ![]() ${{\mathcal {E}}}$ comes from a family of abelian varieties. More precisely, there exist a non-empty open subset
${{\mathcal {E}}}$ comes from a family of abelian varieties. More precisely, there exist a non-empty open subset ![]() $U\subset X$ and an abelian scheme
$U\subset X$ and an abelian scheme ![]() $A_U\rightarrow U$, so that
$A_U\rightarrow U$, so that ![]() $\mathbb {D} (A_U[p^{\infty }])\otimes \overline {\mathbb {Q}}_p\cong \mathcal {E}|_U$.
$\mathbb {D} (A_U[p^{\infty }])\otimes \overline {\mathbb {Q}}_p\cong \mathcal {E}|_U$.
Here, if ![]() $G\rightarrow X$ is a
$G\rightarrow X$ is a ![]() $p$-divisible group,
$p$-divisible group, ![]() $\mathbb {D}(G)$ is the (contravariant) Dieudonné crystal attached to
$\mathbb {D}(G)$ is the (contravariant) Dieudonné crystal attached to ![]() $G$. We have the following applications. Deligne formulated what is now called the companions conjecture in [Reference DeligneDel80, Conjecture 1.2.10(vi)]. For a guide to the crystalline companions conjecture, see [Reference KedlayaKed18, Reference KedlayaKed22].
$G$. We have the following applications. Deligne formulated what is now called the companions conjecture in [Reference DeligneDel80, Conjecture 1.2.10(vi)]. For a guide to the crystalline companions conjecture, see [Reference KedlayaKed18, Reference KedlayaKed22].
Corollary 1.3 Let ![]() $X/\mathbb {F}_q$ be a smooth, geometrically connected, quasi-projective scheme. Let
$X/\mathbb {F}_q$ be a smooth, geometrically connected, quasi-projective scheme. Let ![]() $L_1$ be an irreducible rank
$L_1$ be an irreducible rank ![]() $2$ lisse
$2$ lisse ![]() $\overline {\mathbb {Q}}_l$ sheaf on
$\overline {\mathbb {Q}}_l$ sheaf on ![]() $X$ with infinite monodromy around infinity and determinant
$X$ with infinite monodromy around infinity and determinant ![]() $\overline {\mathbb {Q}}_l(-1)$. Then the following are equivalent:
$\overline {\mathbb {Q}}_l(-1)$. Then the following are equivalent:
(1) there exist a non-empty open subset
 $U\subset X$ and an abelian scheme
$U\subset X$ and an abelian scheme  $\pi \colon A_U\rightarrow U$ such that
$\pi \colon A_U\rightarrow U$ such that  $L_1|_U$ is a summand of
$L_1|_U$ is a summand of  $R^{1}(\pi _U)_*\overline {\mathbb {Q}}_l$;
$R^{1}(\pi _U)_*\overline {\mathbb {Q}}_l$;(2) all crystalline companions to
 $L_1$ exist (as predicted by Deligne's crystalline companions conjecture).
$L_1$ exist (as predicted by Deligne's crystalline companions conjecture).
Corollary 1.4 Let ![]() $X/\mathbb {F}_q$ be a smooth, geometrically connected, quasi-projective scheme. Let
$X/\mathbb {F}_q$ be a smooth, geometrically connected, quasi-projective scheme. Let ![]() ${{\mathcal {E}}}_1$ be an irreducible rank
${{\mathcal {E}}}_1$ be an irreducible rank ![]() $2$ object of
$2$ object of ![]() $\mathbf {F\text{-}Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$ with infinite monodromy around infinity and determinant
$\mathbf {F\text{-}Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$ with infinite monodromy around infinity and determinant ![]() $\overline {\mathbb {Q}}_p(-1)$. Suppose the (number) field
$\overline {\mathbb {Q}}_p(-1)$. Suppose the (number) field ![]() $E_1\subset \overline {\mathbb {Q}}_p$ generated by the coefficients of
$E_1\subset \overline {\mathbb {Q}}_p$ generated by the coefficients of ![]() $P_x({{\mathcal {E}}}_1,t)$ as
$P_x({{\mathcal {E}}}_1,t)$ as ![]() $x$ ranges through the closed points of
$x$ ranges through the closed points of ![]() $X$ has a single prime over
$X$ has a single prime over ![]() $p$. Then
$p$. Then ![]() ${{\mathcal {E}}}_1$ comes from a family of abelian varieties: there exist a non-empty open subset
${{\mathcal {E}}}_1$ comes from a family of abelian varieties: there exist a non-empty open subset ![]() $U\subset X$ and an abelian scheme
$U\subset X$ and an abelian scheme ![]() $A_U\rightarrow U$ such that
$A_U\rightarrow U$ such that ![]() ${{\mathcal {E}}}_1|_U$ is a summand of
${{\mathcal {E}}}_1|_U$ is a summand of ![]() $\mathbb {D}(A_U[p^{\infty }])\otimes \overline {\mathbb {Q}}_p$.
$\mathbb {D}(A_U[p^{\infty }])\otimes \overline {\mathbb {Q}}_p$.
In particular, Corollaries 1.3 and 1.4 provide some evidence for a question of Drinfeld [Reference DrinfeldDri12, Question 1.4] and a conjecture of the authors [Reference Krishnamoorthy and PálKP21, Conjecture 1.2]. Our motivation for formulating this conjecture was a celebrated theorem of Corlette and Simpson over ![]() $\mathbb {C}$ [Reference Corlette and SimpsonCS08, Theorem 11.2], the proof of which uses non-abelian Hodge theory. In contrast to our earlier work [Reference Krishnamoorthy and PálKP21], this paper does not use Serre–Tate deformation theory nor does it use the algebraization/globalization techniques of [Reference HartshorneHar70].
$\mathbb {C}$ [Reference Corlette and SimpsonCS08, Theorem 11.2], the proof of which uses non-abelian Hodge theory. In contrast to our earlier work [Reference Krishnamoorthy and PálKP21], this paper does not use Serre–Tate deformation theory nor does it use the algebraization/globalization techniques of [Reference HartshorneHar70].
We briefly sketch the proof. Drinfeld's first work on the Langlands correspondence for ![]() $\text {GL}_2$, together with Abe's work on the
$\text {GL}_2$, together with Abe's work on the ![]() $p$-adic Langlands correspondence and Lemma 2.5, implies Theorem 1.2 when
$p$-adic Langlands correspondence and Lemma 2.5, implies Theorem 1.2 when ![]() $\dim (X)=1$. (The precise argument is given in Step
$\dim (X)=1$. (The precise argument is given in Step ![]() $2$ of the proof and also uses Remark 2.8 to organize the summands, as explained in Step
$2$ of the proof and also uses Remark 2.8 to organize the summands, as explained in Step ![]() $1$.) Note that the resulting abelian scheme is not unique, but it is unique up to isogeny.
$1$.) Note that the resulting abelian scheme is not unique, but it is unique up to isogeny.
To deal with the higher-dimensional case, we first assume that ![]() $X$ admits a simple normal crossings compactification
$X$ admits a simple normal crossings compactification ![]() $\bar {X}$ and
$\bar {X}$ and ![]() ${{\mathcal {E}}}$ is a logarithmic
${{\mathcal {E}}}$ is a logarithmic ![]() $F$-isocrystal with nilpotent residues. (We recall the notion of logarithmic
$F$-isocrystal with nilpotent residues. (We recall the notion of logarithmic ![]() $F$-isocrystals in Appendix A.) A technique of Katz, combined with slope bounds originally due to Lafforgue, allows one to construct a (non-canonical) logarithmic Dieudonné crystal on an open set
$F$-isocrystals in Appendix A.) A technique of Katz, combined with slope bounds originally due to Lafforgue, allows one to construct a (non-canonical) logarithmic Dieudonné crystal on an open set ![]() $U$ of the compactification
$U$ of the compactification ![]() $\bar {X}$ whose associated logarithmic
$\bar {X}$ whose associated logarithmic ![]() $F$-isocrystal is isomorphic to the restriction
$F$-isocrystal is isomorphic to the restriction ![]() ${{\mathcal {E}}}|_U$. After the work of Kato and Trihan, this logarithmic Dieudonné crystal yields a natural line bundle, which we call the Hodge bundle
${{\mathcal {E}}}|_U$. After the work of Kato and Trihan, this logarithmic Dieudonné crystal yields a natural line bundle, which we call the Hodge bundle ![]() $\omega$ of the logarithmic Dieudonné crystal, on
$\omega$ of the logarithmic Dieudonné crystal, on ![]() $\bar {X}$.
$\bar {X}$.
For any odd prime ![]() $l\neq p$, let
$l\neq p$, let ![]() $\mathscr {A}_{h,1,l}$ denote the moduli space of principally polarized abelian schemes of dimension
$\mathscr {A}_{h,1,l}$ denote the moduli space of principally polarized abelian schemes of dimension ![]() $h$ equipped with full level
$h$ equipped with full level ![]() $l$ structure over
$l$ structure over ![]() $\operatorname {Spec}({{\mathbb {Z}}}[1/l])$. It is well known that the Hodge line bundle is ample on
$\operatorname {Spec}({{\mathbb {Z}}}[1/l])$. It is well known that the Hodge line bundle is ample on ![]() $\mathscr {A}_{h,1,l}$ over
$\mathscr {A}_{h,1,l}$ over ![]() $\operatorname {Spec}({{\mathbb {Z}}}[1/l])$. We use Poonen's Bertini theorem over finite fields together with Drinfeld's result and Zarhin's trick to find a well-adapted family of extremely ample space-filling curves
$\operatorname {Spec}({{\mathbb {Z}}}[1/l])$. We use Poonen's Bertini theorem over finite fields together with Drinfeld's result and Zarhin's trick to find a well-adapted family of extremely ample space-filling curves ![]() $\bar {C}_n$ of
$\bar {C}_n$ of ![]() $\bar {X}$ that each map to the minimal compactification
$\bar {X}$ that each map to the minimal compactification ![]() $\mathscr {A}^{*}_{h,1,l}\subset \mathbb {P}^{m}$ via some fixed power of the Hodge bundle
$\mathscr {A}^{*}_{h,1,l}\subset \mathbb {P}^{m}$ via some fixed power of the Hodge bundle ![]() $\omega |_{\bar {C}_n}^{r}$. (This step uses foundational work of Étesse, Kato, Kedlaya, and Trihan that we explain in Appendix A.) Note that
$\omega |_{\bar {C}_n}^{r}$. (This step uses foundational work of Étesse, Kato, Kedlaya, and Trihan that we explain in Appendix A.) Note that ![]() $H^{0}(\bar {X},\omega ^{r})$ is a finite-dimensional vector space over a finite field and is hence a finite set. We use this finiteness together with the pigeonhole principle to prove that infinitely many of these maps can be pieced together into a rational map
$H^{0}(\bar {X},\omega ^{r})$ is a finite-dimensional vector space over a finite field and is hence a finite set. We use this finiteness together with the pigeonhole principle to prove that infinitely many of these maps can be pieced together into a rational map ![]() $\bar {X}\dashrightarrow \mathscr {A}_{h,1,l}\subset \mathbb {P}^{m}$. Therefore we obtain an abelian scheme
$\bar {X}\dashrightarrow \mathscr {A}_{h,1,l}\subset \mathbb {P}^{m}$. Therefore we obtain an abelian scheme ![]() $\psi _U\colon B_U\rightarrow U$ over some open
$\psi _U\colon B_U\rightarrow U$ over some open ![]() $U\subset X$. The space-filling properties of the
$U\subset X$. The space-filling properties of the ![]() $\bar {C}_n$ and Zarhin's work on the Tate isogeny theorem for fields finitely generated over
$\bar {C}_n$ and Zarhin's work on the Tate isogeny theorem for fields finitely generated over ![]() $\mathbb {F}_q$ then allow us to conclude.
$\mathbb {F}_q$ then allow us to conclude.
To deduce the general case, we use Kedlaya's semi-stable reduction theorem for overconvergent ![]() $F$-isocrystals.
$F$-isocrystals.
Remark 1.5 We comment on the relation of this paper to [Reference Krishnamoorthy and PálKP21]. In [Reference Krishnamoorthy and PálKP21] we prove a Lefschetz-style theorem for families of ![]() $\mathrm {GL}_2$-type abelian schemes over finite fields. This has the following implication for [Reference Krishnamoorthy and PálKP21, Conjecture 1.2]: if
$\mathrm {GL}_2$-type abelian schemes over finite fields. This has the following implication for [Reference Krishnamoorthy and PálKP21, Conjecture 1.2]: if ![]() $X/\mathbb {F}_q$ is a smooth projective variety, then there exists an ample curve
$X/\mathbb {F}_q$ is a smooth projective variety, then there exists an ample curve ![]() $C\subset X$ such that if
$C\subset X$ such that if ![]() ${{\mathcal {E}}}\in \textbf {F-Isoc}({X})_{\overline {\mathbb {Q}}_p}$ and
${{\mathcal {E}}}\in \textbf {F-Isoc}({X})_{\overline {\mathbb {Q}}_p}$ and ![]() ${{\mathcal {E}}}|_C$ comes from an abelian scheme
${{\mathcal {E}}}|_C$ comes from an abelian scheme ![]() $A_C\rightarrow C$ of
$A_C\rightarrow C$ of ![]() $\mathrm {GL}_2$-type, then there is an open subset
$\mathrm {GL}_2$-type, then there is an open subset ![]() $U\subset X$ such that
$U\subset X$ such that ![]() ${{\mathcal {E}}}|_U$ comes from an abelian scheme
${{\mathcal {E}}}|_U$ comes from an abelian scheme ![]() $B_U\rightarrow U$ of
$B_U\rightarrow U$ of ![]() $\mathrm {GL}_2$-type. (It follows from Zarhin's work on the Tate isogeny conjecture that
$\mathrm {GL}_2$-type. (It follows from Zarhin's work on the Tate isogeny conjecture that ![]() $B_C\rightarrow C$ is indeed isogenous to
$B_C\rightarrow C$ is indeed isogenous to ![]() $A_C\rightarrow C$.) To prove this, we use Serre–Tate deformation theory and globalization results of [Reference HartshorneHar70], the latter of which critically uses the positivity of
$A_C\rightarrow C$.) To prove this, we use Serre–Tate deformation theory and globalization results of [Reference HartshorneHar70], the latter of which critically uses the positivity of ![]() $C$ in
$C$ in ![]() $X$. In this paper, we only deal with non-proper varieties
$X$. In this paper, we only deal with non-proper varieties ![]() $X/\mathbb {F}_q$ and we use infinitely many (space-filling, affine) curves together with a result of Drinfeld, which is only known for affine curves. In particular, the main results of [Reference Krishnamoorthy and PálKP21] do not imply the main result of this paper.
$X/\mathbb {F}_q$ and we use infinitely many (space-filling, affine) curves together with a result of Drinfeld, which is only known for affine curves. In particular, the main results of [Reference Krishnamoorthy and PálKP21] do not imply the main result of this paper.
2. Preliminaries
Before proving Theorem 1.2, we need several preliminary results. A key ingredient in the proof is the following theorem, which is a byproduct of Drinfeld's first work on the Langlands correspondence for ![]() $\mathrm {GL}_2$.
$\mathrm {GL}_2$.
Theorem 2.1 (Drinfeld)
Let ![]() $C/\mathbb {F}_q$ be a smooth affine curve and let
$C/\mathbb {F}_q$ be a smooth affine curve and let ![]() $L_1$ be a rank
$L_1$ be a rank ![]() $2$ irreducible
$2$ irreducible ![]() $\overline {\mathbb {Q}}_l$ sheaf with determinant
$\overline {\mathbb {Q}}_l$ sheaf with determinant ![]() $\overline {\mathbb {Q}}_l(-1)$. Suppose
$\overline {\mathbb {Q}}_l(-1)$. Suppose ![]() $L_1$ has infinite local monodromy around some point at
$L_1$ has infinite local monodromy around some point at ![]() $\infty \in \overline {C}\backslash C$. Then
$\infty \in \overline {C}\backslash C$. Then ![]() $L_1$ comes from a family of abelian varieties in the following sense. Let
$L_1$ comes from a family of abelian varieties in the following sense. Let ![]() $E$ be the field generated by the Frobenius traces of
$E$ be the field generated by the Frobenius traces of ![]() $L_1$ and suppose
$L_1$ and suppose ![]() $[E:{{\mathbb {Q}}}]=g$. Then there exist an abelian scheme
$[E:{{\mathbb {Q}}}]=g$. Then there exist an abelian scheme
of dimension ![]() $g$ and an isomorphism
$g$ and an isomorphism ![]() $E\cong \textrm {End}_{C}(A)\otimes {{\mathbb {Q}}}$, realizing
$E\cong \textrm {End}_{C}(A)\otimes {{\mathbb {Q}}}$, realizing ![]() $A_C$ as a
$A_C$ as a ![]() $\mathrm {GL}_{2}$-type abelian scheme, such that
$\mathrm {GL}_{2}$-type abelian scheme, such that ![]() $L_1$ occurs as a summand of
$L_1$ occurs as a summand of ![]() $R^{1}(\pi _C)_*\overline {\mathbb {Q}}_l$. Moreover,
$R^{1}(\pi _C)_*\overline {\mathbb {Q}}_l$. Moreover, ![]() $A_{C}\rightarrow C$ is totally degenerate around
$A_{C}\rightarrow C$ is totally degenerate around ![]() $\infty$.
$\infty$.
See [Reference Snowden and TsimermanST18, Proof of Proposition 19, Remark 20] for how to recover this result from Drinfeld's work. This amounts to combining [Reference DrinfeldDri83, Main Theorem, Remark 5] with [Reference Drinfel'dDri77, Theorem 1].
For completeness, we briefly recall the theory of companions and what is known about them. For a thorough summary about the definitions and also what is known, we refer the reader to [Reference KedlayaKed18]. Alternatively, the reader may see [Reference Krishnamoorthy and PálKP21, § 4].
Definition 2.2 Let ![]() $X/\mathbb {F}_q$ be a smooth, geometrically connected variety. Let
$X/\mathbb {F}_q$ be a smooth, geometrically connected variety. Let ![]() $\lambda$ be a prime number and let
$\lambda$ be a prime number and let ![]() $\mathcal {E}$ denote either a smooth
$\mathcal {E}$ denote either a smooth ![]() $\overline {\mathbb {Q}}_{\lambda }$ sheaf on
$\overline {\mathbb {Q}}_{\lambda }$ sheaf on ![]() $X$ if
$X$ if ![]() $\lambda \neq p$ or an overconvergent
$\lambda \neq p$ or an overconvergent ![]() $F$-isocrystal with coefficients in
$F$-isocrystal with coefficients in ![]() $\overline {\mathbb {Q}}_p$ if
$\overline {\mathbb {Q}}_p$ if ![]() $\lambda =p$. Following Kedlaya [Reference KedlayaKed18, § 1], we call such
$\lambda =p$. Following Kedlaya [Reference KedlayaKed18, § 1], we call such ![]() ${{\mathcal {E}}}$ coefficient objects.
${{\mathcal {E}}}$ coefficient objects.
(1) Let
 $l\neq p$ be a prime number and let
$l\neq p$ be a prime number and let  $L$ be a lisse
$L$ be a lisse  $\overline {\mathbb {Q}}_l$-sheaf on
$\overline {\mathbb {Q}}_l$-sheaf on  $X$. Fix a (possibly non-continuous) field isomorphism
$X$. Fix a (possibly non-continuous) field isomorphism  $\iota \colon \overline {\mathbb {Q}}_{\lambda }\rightarrow \overline {\mathbb {Q}}_l$. We say that
$\iota \colon \overline {\mathbb {Q}}_{\lambda }\rightarrow \overline {\mathbb {Q}}_l$. We say that  $L$ is an
$L$ is an  $\iota$-companion of
$\iota$-companion of  $\mathcal {E}$ if, for all closed points
$\mathcal {E}$ if, for all closed points  $x\in X$, we have
where
$x\in X$, we have
where \[ \iota(P_x(\mathcal{E},t))=P_x(L,t)\in \overline{\mathbb{Q}}_l[t], \]
\[ \iota(P_x(\mathcal{E},t))=P_x(L,t)\in \overline{\mathbb{Q}}_l[t], \] $P_x(-,t)$ denotes the reverse characteristic polynomial at the closed point
$P_x(-,t)$ denotes the reverse characteristic polynomial at the closed point  $x$.
$x$.(2) Let
 $\mathcal {F}$ be an overconvergent
$\mathcal {F}$ be an overconvergent  $F$-isocrystal on
$F$-isocrystal on  $X$ with coefficients in
$X$ with coefficients in  $\overline {\mathbb {Q}}_p$ and fix an isomorphism
$\overline {\mathbb {Q}}_p$ and fix an isomorphism  $\iota \colon \overline {\mathbb {Q}}_{\lambda }\rightarrow \overline {\mathbb {Q}}_p$. We say
$\iota \colon \overline {\mathbb {Q}}_{\lambda }\rightarrow \overline {\mathbb {Q}}_p$. We say  $\mathcal {F}$ is an
$\mathcal {F}$ is an  $\iota$-companion of
$\iota$-companion of  $\mathcal {E}$ if, for all closed points
$\mathcal {E}$ if, for all closed points  $x\in X$, we have
$x\in X$, we have
 \[ \iota(P_x(\mathcal{E},t))=P_x(\mathcal{F},t)\in \overline{\mathbb{Q}}_p[t]. \]
\[ \iota(P_x(\mathcal{E},t))=P_x(\mathcal{F},t)\in \overline{\mathbb{Q}}_p[t]. \]
In either of these cases, we say that the ![]() $\iota$-companion to
$\iota$-companion to ![]() $\mathcal {E}$ exists.
$\mathcal {E}$ exists.
Suppose ![]() $\mathcal {E}$ is semi-simple and each irreducible summand has algebraic determinant. Then Deligne's conjecture, together with Crew's
$\mathcal {E}$ is semi-simple and each irreducible summand has algebraic determinant. Then Deligne's conjecture, together with Crew's ![]() $p$-adic enhancement, predict that all
$p$-adic enhancement, predict that all ![]() $\iota$-companions to
$\iota$-companions to ![]() ${{\mathcal {E}}}$ exist. It follows from work of Abe, Abe and Esnault, Deligne, Drinfeld, Kedlaya, and Lafforgue [Reference Abe and EsnaultAE19, Reference AbeAbe18, Reference DeligneDel12, Reference DrinfeldDri12, Reference LafforgueLaf02] that this conjecture is known to hold in the following cases.
${{\mathcal {E}}}$ exist. It follows from work of Abe, Abe and Esnault, Deligne, Drinfeld, Kedlaya, and Lafforgue [Reference Abe and EsnaultAE19, Reference AbeAbe18, Reference DeligneDel12, Reference DrinfeldDri12, Reference LafforgueLaf02] that this conjecture is known to hold in the following cases.
Theorem 2.3 Let ![]() $X/\mathbb {F}_q$ be a smooth, geometrically connected variety. Let
$X/\mathbb {F}_q$ be a smooth, geometrically connected variety. Let ![]() $\mathcal {E}$ be a semi-simple coefficient object on
$\mathcal {E}$ be a semi-simple coefficient object on ![]() $X$ such that the irreducible summands have algebraic determinant.
$X$ such that the irreducible summands have algebraic determinant.
• If
 $\dim (X)=1$, then all
$\dim (X)=1$, then all  $\iota$-companions exist ([Reference LafforgueLaf02, Théorème VII.6] and [Reference AbeAbe18, Theorem 4.4.1]).
$\iota$-companions exist ([Reference LafforgueLaf02, Théorème VII.6] and [Reference AbeAbe18, Theorem 4.4.1]).• For any
 $l\neq p$ and any isomorphism
$l\neq p$ and any isomorphism  $\iota \colon \overline {\mathbb {Q}}_{\lambda }\rightarrow \overline {\mathbb {Q}}_l$, the
$\iota \colon \overline {\mathbb {Q}}_{\lambda }\rightarrow \overline {\mathbb {Q}}_l$, the  $\iota$-companion to
$\iota$-companion to  $\mathcal {E}$ exists ([Reference DrinfeldDri12, Theorem 1.1] and [Reference Abe and EsnaultAE19, Theorem 4.2] or [Reference KedlayaKed18, Theorem 0.4.1]).
$\mathcal {E}$ exists ([Reference DrinfeldDri12, Theorem 1.1] and [Reference Abe and EsnaultAE19, Theorem 4.2] or [Reference KedlayaKed18, Theorem 0.4.1]).
In particular, ![]() $p$-adic companions are not known to exist when
$p$-adic companions are not known to exist when ![]() $\dim (X)>1$, although Kedlaya has recently proposed a promising strategy [Reference KedlayaKed21].
$\dim (X)>1$, although Kedlaya has recently proposed a promising strategy [Reference KedlayaKed21].
Proposition 2.4 Maintain the hypotheses of Theorem 1.2. Let ![]() $\iota \colon \overline {\mathbb {Q}}_p\rightarrow \overline {\mathbb {Q}}_l$ be a field isomorphism and let
$\iota \colon \overline {\mathbb {Q}}_p\rightarrow \overline {\mathbb {Q}}_l$ be a field isomorphism and let ![]() $L:=\ ^{\iota }{{\mathcal {E}}}$ be the (semi-simple)
$L:=\ ^{\iota }{{\mathcal {E}}}$ be the (semi-simple) ![]() $\iota$-companion to
$\iota$-companion to ![]() ${{\mathcal {E}}}$.
${{\mathcal {E}}}$.
• The isomorphism class of
 $L$ is independent of the choice of
$L$ is independent of the choice of  $\iota$.
$\iota$.• Let
 $L_i$ be an irreducible summand of
$L_i$ be an irreducible summand of  $L$. Then
$L$. Then  $L_i$ has rank 2, determinant
$L_i$ has rank 2, determinant  $\overline {\mathbb {Q}}_l(-1)$, and infinite monodromy at infinity.
$\overline {\mathbb {Q}}_l(-1)$, and infinite monodromy at infinity.
Proof. For all closed points ![]() $x$ of
$x$ of ![]() $X$, we have that
$X$, we have that ![]() $P_x(L,t)\in {{\mathbb {Q}}}[t]\subset \overline {\mathbb {Q}}_l[t]$ as
$P_x(L,t)\in {{\mathbb {Q}}}[t]\subset \overline {\mathbb {Q}}_l[t]$ as ![]() $\iota ({{\mathbb {Q}}})={{\mathbb {Q}}}\subset \overline {\mathbb {Q}}_l$. The first statement then follows from the Cebotarev density theorem and the Brauer–Nesbitt theorem.
$\iota ({{\mathbb {Q}}})={{\mathbb {Q}}}\subset \overline {\mathbb {Q}}_l$. The first statement then follows from the Cebotarev density theorem and the Brauer–Nesbitt theorem.
If ![]() ${{\mathcal {E}}}_i$ is an irreducible summand of
${{\mathcal {E}}}_i$ is an irreducible summand of ![]() ${{\mathcal {E}}}$, then
${{\mathcal {E}}}$, then ![]() $^{\iota }{{\mathcal {E}}}_i$ is an irreducible
$^{\iota }{{\mathcal {E}}}_i$ is an irreducible ![]() $\overline {\mathbb {Q}}_l$-sheaf by [Reference KedlayaKed18, Theorem 3.3.1]. As the companions relation commutes with direct sum, it follows that if
$\overline {\mathbb {Q}}_l$-sheaf by [Reference KedlayaKed18, Theorem 3.3.1]. As the companions relation commutes with direct sum, it follows that if ![]() ${{\mathcal {E}}}\cong \oplus {{\mathcal {E}}}_i^{m_i}$ is the decomposition of
${{\mathcal {E}}}\cong \oplus {{\mathcal {E}}}_i^{m_i}$ is the decomposition of ![]() ${{\mathcal {E}}}$ into irreducible objects in
${{\mathcal {E}}}$ into irreducible objects in ![]() $\textbf {F-Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$, then
$\textbf {F-Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$, then ![]() $L\cong \oplus (^{\iota }{{\mathcal {E}}}_i)^{m_i}$ is a decomposition of
$L\cong \oplus (^{\iota }{{\mathcal {E}}}_i)^{m_i}$ is a decomposition of ![]() $L$ into irreducible lisse
$L$ into irreducible lisse ![]() $\overline {\mathbb {Q}}_l$-sheaves on
$\overline {\mathbb {Q}}_l$-sheaves on ![]() $X$. One may observe that
$X$. One may observe that ![]() $\det (^{\iota }{{\mathcal {E}}}_i)\cong \overline {\mathbb {Q}}_l(-1)$ because, for every closed point
$\det (^{\iota }{{\mathcal {E}}}_i)\cong \overline {\mathbb {Q}}_l(-1)$ because, for every closed point ![]() $x$ of
$x$ of ![]() $X$, the constant term of
$X$, the constant term of ![]() $P_x({{\mathcal {E}}}_i,t)$ is
$P_x({{\mathcal {E}}}_i,t)$ is ![]() $q$ and hence the constant term of
$q$ and hence the constant term of ![]() $P_x(^{\iota }{{\mathcal {E}}}_i,t)$ is also
$P_x(^{\iota }{{\mathcal {E}}}_i,t)$ is also ![]() $q$. Finally, suppose for contradiction that there exists an
$q$. Finally, suppose for contradiction that there exists an ![]() $i$ with
$i$ with ![]() $L_i:=\ ^{\iota }{{\mathcal {E}}}_i$ having finite local monodromy at infinity. Then there exist a smooth projective variety
$L_i:=\ ^{\iota }{{\mathcal {E}}}_i$ having finite local monodromy at infinity. Then there exist a smooth projective variety ![]() $\bar {X}'/\mathbb {F}_q$, an open dense subscheme
$\bar {X}'/\mathbb {F}_q$, an open dense subscheme ![]() $X'\subset \bar {X}'$, and an alteration
$X'\subset \bar {X}'$, and an alteration ![]() $f\colon X'\rightarrow X$ such that
$f\colon X'\rightarrow X$ such that ![]() $f^{*}L_i$ extends to
$f^{*}L_i$ extends to ![]() $\bar {X}'$. It follows from [Reference KedlayaKed18, Corollary 3.3.3] that
$\bar {X}'$. It follows from [Reference KedlayaKed18, Corollary 3.3.3] that ![]() $f^{*}{{\mathcal {E}}}_i$ also extends to
$f^{*}{{\mathcal {E}}}_i$ also extends to ![]() $\bar {X}'$, contradicting the hypothesis that
$\bar {X}'$, contradicting the hypothesis that ![]() ${{\mathcal {E}}}_i$ had infinite local monodromy at infinity.
${{\mathcal {E}}}_i$ had infinite local monodromy at infinity.
We will need the following lemma to ensure that, given the hypotheses of Theorem 1.2, every ![]() $p$-adic companion of
$p$-adic companion of ![]() ${{\mathcal {E}}}_i$ is again a summand of
${{\mathcal {E}}}_i$ is again a summand of ![]() ${{\mathcal {E}}}$; moreover, the companion relation preserves multiplicity in the isotypic decomposition of
${{\mathcal {E}}}$; moreover, the companion relation preserves multiplicity in the isotypic decomposition of ![]() ${{\mathcal {E}}}$.
${{\mathcal {E}}}$.
Lemma 2.5 Let ![]() $X/\mathbb {F}_q$ be a smooth, geometrically connected scheme.
$X/\mathbb {F}_q$ be a smooth, geometrically connected scheme.
(1) Let
 $l\neq p$ be a prime and let
$l\neq p$ be a prime and let  $L$ be a lisse, semi-simple
$L$ be a lisse, semi-simple  $\overline {\mathbb {Q}}_l$-sheaf on
$\overline {\mathbb {Q}}_l$-sheaf on  $X$, all of whose irreducible summands
$X$, all of whose irreducible summands  $L_i$ have algebraic determinant. Suppose that, for all closed points
$L_i$ have algebraic determinant. Suppose that, for all closed points  $x$ of
$x$ of  $X$, we have
Let
$X$, we have
Let \[ P_x(L,t)\in {{\mathbb{Q}}}[t]\subset \overline{\mathbb{Q}}_l[t]. \]
\[ P_x(L,t)\in {{\mathbb{Q}}}[t]\subset \overline{\mathbb{Q}}_l[t]. \] $L_i$ be an irreducible summand of
$L_i$ be an irreducible summand of  $L$ that occurs with multiplicity
$L$ that occurs with multiplicity  $m_i$ and
$m_i$ and  $\iota \in \text {Aut}_{{{\mathbb {Q}}}}(\overline {\mathbb {Q}}_l)$ be a field automorphism. Then the
$\iota \in \text {Aut}_{{{\mathbb {Q}}}}(\overline {\mathbb {Q}}_l)$ be a field automorphism. Then the  $\iota$-companion to
$\iota$-companion to  $L_i$, denoted
$L_i$, denoted  $^{\iota }L_i$, is isomorphic to an irreducible summand of
$^{\iota }L_i$, is isomorphic to an irreducible summand of  $L$ that occurs with multiplicity
$L$ that occurs with multiplicity  $m_i$.
$m_i$.(2) Let
 ${{\mathcal {F}}}$ be a semi-simple object of
${{\mathcal {F}}}$ be a semi-simple object of  $\,\mathbf {F\text{-}Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$, all of whose irreducible summands
$\,\mathbf {F\text{-}Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$, all of whose irreducible summands  ${{\mathcal {F}}}_i$ have algebraic determinant. Suppose that, for all closed points
${{\mathcal {F}}}_i$ have algebraic determinant. Suppose that, for all closed points  $x$ of
$x$ of  $X$, we have
Let
$X$, we have
Let \[ P_x({{\mathcal{F}}},t)\in {{\mathbb{Q}}}[t]\subset \overline{\mathbb{Q}}_p[t]. \]
\[ P_x({{\mathcal{F}}},t)\in {{\mathbb{Q}}}[t]\subset \overline{\mathbb{Q}}_p[t]. \] ${{\mathcal {F}}}_i$ be an irreducible summand of
${{\mathcal {F}}}_i$ be an irreducible summand of  ${{\mathcal {F}}}$ that occurs with multiplicity
${{\mathcal {F}}}$ that occurs with multiplicity  $m_i$. Let
$m_i$. Let  $\iota \in \text {Aut}_{{{\mathbb {Q}}}}(\overline {\mathbb {Q}}_p)$. Then the
$\iota \in \text {Aut}_{{{\mathbb {Q}}}}(\overline {\mathbb {Q}}_p)$. Then the  $\iota$-companion of
$\iota$-companion of  ${{\mathcal {F}}}_i$, denoted by
${{\mathcal {F}}}_i$, denoted by  $^{\iota }{{\mathcal {F}}}_i$, exists and is isomorphic to a direct summand of
$^{\iota }{{\mathcal {F}}}_i$, exists and is isomorphic to a direct summand of  ${{\mathcal {F}}}$ that occurs with multiplicity
${{\mathcal {F}}}$ that occurs with multiplicity  $m_i$.
$m_i$.
Proof. We reduce the crystalline case to the étale case. (Note that we could have equivalently proceeded by reduction to curves using [Reference Abe and EsnaultAE19].) As ![]() ${{\mathcal {F}}}$ is semi-simple, write an isotypic decomposition:
${{\mathcal {F}}}$ is semi-simple, write an isotypic decomposition:
 \[ \displaystyle {{\mathcal{F}}}\cong \bigoplus_{i=1}^{a}{{\mathcal{F}}}_i^{m_i}. \]
\[ \displaystyle {{\mathcal{F}}}\cong \bigoplus_{i=1}^{a}{{\mathcal{F}}}_i^{m_i}. \]
Note that each ![]() ${{\mathcal {F}}}_i$ is pure by [Reference Abe and EsnaultAE19, Theorem 2.7]. Fix an isomorphism
${{\mathcal {F}}}_i$ is pure by [Reference Abe and EsnaultAE19, Theorem 2.7]. Fix an isomorphism ![]() $\sigma \colon \overline {\mathbb {Q}}_p\rightarrow \overline {\mathbb {Q}}_l$. By [Reference Abe and EsnaultAE19, Theorem 4.2] or [Reference KedlayaKed18, Corollary 3.5.3], the
$\sigma \colon \overline {\mathbb {Q}}_p\rightarrow \overline {\mathbb {Q}}_l$. By [Reference Abe and EsnaultAE19, Theorem 4.2] or [Reference KedlayaKed18, Corollary 3.5.3], the ![]() $\sigma$-companion to each
$\sigma$-companion to each ![]() ${{\mathcal {F}}}_i$ exists as an irreducible lisse
${{\mathcal {F}}}_i$ exists as an irreducible lisse ![]() $\overline {\mathbb {Q}}_l$-sheaf
$\overline {\mathbb {Q}}_l$-sheaf ![]() $L_i$. Setting
$L_i$. Setting ![]() $L$ to be the semi-simple
$L$ to be the semi-simple ![]() $\sigma$-companion of
$\sigma$-companion of ![]() ${{\mathcal {F}}}$, we have
${{\mathcal {F}}}$, we have
 \[ \displaystyle L\cong \bigoplus_{i=1}^{a}L_i^{m_i}. \]
\[ \displaystyle L\cong \bigoplus_{i=1}^{a}L_i^{m_i}. \] Set ![]() $\iota \in \text {Aut}_{{{\mathbb {Q}}}}(\overline {\mathbb {Q}}_p)$. Then
$\iota \in \text {Aut}_{{{\mathbb {Q}}}}(\overline {\mathbb {Q}}_p)$. Then ![]() ${{\mathcal {F}}}_j$ is the
${{\mathcal {F}}}_j$ is the ![]() $\iota$-companion to
$\iota$-companion to ![]() ${{\mathcal {F}}}_i$ if and only if
${{\mathcal {F}}}_i$ if and only if ![]() $L_j$ is the
$L_j$ is the ![]() $\sigma \circ \iota \circ \sigma ^{-1}$-companion to
$\sigma \circ \iota \circ \sigma ^{-1}$-companion to ![]() $L_i$. Therefore it suffices to prove the result in the étale setting.
$L_i$. Therefore it suffices to prove the result in the étale setting.
Let ![]() $M$ be an irreducible lisse
$M$ be an irreducible lisse ![]() $\overline {\mathbb {Q}}_l$-sheaf on
$\overline {\mathbb {Q}}_l$-sheaf on ![]() $X$. Then
$X$. Then ![]() $M$ is pure by [Reference DeligneDel12, Théorème 1.6] and class field theory. Then the multiplicity of
$M$ is pure by [Reference DeligneDel12, Théorème 1.6] and class field theory. Then the multiplicity of ![]() $M$ in the semi-simple sheaf
$M$ in the semi-simple sheaf ![]() $L$ is
$L$ is ![]() $\dim (H^{0}(X,M^{*}\otimes L))$. By assumption we have that, for all closed points
$\dim (H^{0}(X,M^{*}\otimes L))$. By assumption we have that, for all closed points ![]() $x$ of
$x$ of ![]() $X$,
$X$, ![]() $P_x(L,t)\in {{\mathbb {Q}}}[t]\subset \overline {\mathbb {Q}}_l[t]$. Let
$P_x(L,t)\in {{\mathbb {Q}}}[t]\subset \overline {\mathbb {Q}}_l[t]$. Let ![]() $\iota \in \textrm {Aut}_{{{\mathbb {Q}}}}(\overline {\mathbb {Q}}_l)$, and note that the semi-simple
$\iota \in \textrm {Aut}_{{{\mathbb {Q}}}}(\overline {\mathbb {Q}}_l)$, and note that the semi-simple ![]() $\iota$-companion to
$\iota$-companion to ![]() $L$ is again isomorphic to
$L$ is again isomorphic to ![]() $L$. Then we claim that the
$L$. Then we claim that the ![]() $\iota$-companion to
$\iota$-companion to ![]() $M^{*}\otimes L$ is isomorphic to
$M^{*}\otimes L$ is isomorphic to ![]() $(^{\iota } M^{*})\otimes L$. Indeed, this follows from the following two facts. First of all, both
$(^{\iota } M^{*})\otimes L$. Indeed, this follows from the following two facts. First of all, both ![]() $M^{*}\otimes L$ and
$M^{*}\otimes L$ and ![]() $(^{\iota } M^{*})\otimes L$, being the tensor product of semi-simple representations of characteristic 0, are semi-simple. Second, it follows from the fundamental theorem of symmetric functions that for fixed
$(^{\iota } M^{*})\otimes L$, being the tensor product of semi-simple representations of characteristic 0, are semi-simple. Second, it follows from the fundamental theorem of symmetric functions that for fixed ![]() $d,e\in \mathbb {N}$ there exist universal polynomials
$d,e\in \mathbb {N}$ there exist universal polynomials ![]() $(u_i)_{i=0}^{de}$ in the ring
$(u_i)_{i=0}^{de}$ in the ring ![]() $\mathbb {Q}[\alpha _1,\dots,\alpha _d,\beta _1,\dots,\beta _e]$ with the following property. Let
$\mathbb {Q}[\alpha _1,\dots,\alpha _d,\beta _1,\dots,\beta _e]$ with the following property. Let ![]() $V$ and
$V$ and ![]() $W$ be finite-dimensional vector spaces over a field
$W$ be finite-dimensional vector spaces over a field ![]() $K$ of characteristic 0 and of dimensions
$K$ of characteristic 0 and of dimensions ![]() $d$ and
$d$ and ![]() $e$ and let
$e$ and let ![]() $A$ and
$A$ and ![]() $B$ be linear operators on
$B$ be linear operators on ![]() $V$ and
$V$ and ![]() $W$, respectively. Write
$W$, respectively. Write ![]() $P(A,t)=\sum _{i=0}^{d}a_it^{i}$ and
$P(A,t)=\sum _{i=0}^{d}a_it^{i}$ and ![]() $P(B,t)=\sum _{j=0}^{e}b_jt^{j}$ for the reverse characteristic polynomials of
$P(B,t)=\sum _{j=0}^{e}b_jt^{j}$ for the reverse characteristic polynomials of ![]() $A$ and
$A$ and ![]() $B$. Then the reverse characteristic polynomial
$B$. Then the reverse characteristic polynomial ![]() $P(A\otimes B,t)$ of
$P(A\otimes B,t)$ of ![]() $A\otimes B$ is equal to
$A\otimes B$ is equal to
 \[ \displaystyle P(A\otimes B,t)=\sum_{k=0}^{de}u_k(a_0,\dots,a_d,b_0,\dots,b_e)t^{k}. \]
\[ \displaystyle P(A\otimes B,t)=\sum_{k=0}^{de}u_k(a_0,\dots,a_d,b_0,\dots,b_e)t^{k}. \] Translating back, let ![]() $x$ be a closed point of
$x$ be a closed point of ![]() $X$ and write
$X$ and write ![]() $P_x(M^{*},t)=\sum _{i=0}^{d} a_it^{i}$ and
$P_x(M^{*},t)=\sum _{i=0}^{d} a_it^{i}$ and ![]() $P_x(L,t)=\sum _{j=0}^{e} b_jt^{j}$. Then we have
$P_x(L,t)=\sum _{j=0}^{e} b_jt^{j}$. Then we have
 \[ \displaystyle P_x(M^{*}\otimes L,t)=\sum_{k=0}^{de}u_k(a_0,\dots,a_d,b_0,\dots,b_e)t^{k}. \]
\[ \displaystyle P_x(M^{*}\otimes L,t)=\sum_{k=0}^{de}u_k(a_0,\dots,a_d,b_0,\dots,b_e)t^{k}. \]It follows that
 \[ P_x(^{\iota}(M^{*}\otimes L),t)=P_x((^{\iota}M^{*})\otimes\ ^{\iota}L,t)=\sum_{k=0}^{de}u_k(\iota(a_0),\dots,\iota(a_d),\iota(b_0),\dots,\iota(b_e))t^{k}. \]
\[ P_x(^{\iota}(M^{*}\otimes L),t)=P_x((^{\iota}M^{*})\otimes\ ^{\iota}L,t)=\sum_{k=0}^{de}u_k(\iota(a_0),\dots,\iota(a_d),\iota(b_0),\dots,\iota(b_e))t^{k}. \]
But ![]() $\iota (b_j)=b_j$ because
$\iota (b_j)=b_j$ because ![]() $b_j\in \mathbb {Q}$ for all
$b_j\in \mathbb {Q}$ for all ![]() $j$. Therefore
$j$. Therefore ![]() $P_x(^{\iota }(M^{*}\otimes L),t)=P_x(^{\iota }(M^{*})\otimes L,t)$. The semi-simplicity of
$P_x(^{\iota }(M^{*}\otimes L),t)=P_x(^{\iota }(M^{*})\otimes L,t)$. The semi-simplicity of ![]() $^{\iota }(M^{*}\otimes L)$ and
$^{\iota }(M^{*}\otimes L)$ and ![]() $^{\iota }M^{*}\otimes L$ allows us to conclude that
$^{\iota }M^{*}\otimes L$ allows us to conclude that ![]() $^{\iota }(M^{*}\otimes L)$ is isomorphic to
$^{\iota }(M^{*}\otimes L)$ is isomorphic to ![]() $^{\iota }M^{*}\otimes L$.
$^{\iota }M^{*}\otimes L$.
On the other hand, the exact argument of [Reference Abe and EsnaultAE19, 3.2] for lisse ![]() $l$-adic sheaves implies that
$l$-adic sheaves implies that ![]() $\dim (H^{0}(X,M^{*}\otimes L))=\dim (H^{0}(X,\ ^{\iota }(M^{*} \otimes L))$. Therefore
$\dim (H^{0}(X,M^{*}\otimes L))=\dim (H^{0}(X,\ ^{\iota }(M^{*} \otimes L))$. Therefore ![]() $\dim (H^{0}(X,M^{*}\otimes L))=\dim (H^{0}(X,(^{\iota }M^{*})\otimes L))$, and the result follows.
$\dim (H^{0}(X,M^{*}\otimes L))=\dim (H^{0}(X,(^{\iota }M^{*})\otimes L))$, and the result follows.
Remark 2.6 The argument of [Reference Abe and EsnaultAE19, 3.2] cited in the proof of Lemma 2.5 is based on [Reference LafforgueLaf02, Corollary VI.3] and uses ![]() $L$-functions. A similar idea is used in the proof that the companions relations preserves irreducibility, which was crucial to Proposition 2.4. See also [Reference KedlayaKed18, Lemma 3.1.5, Theorem 3.3.1].
$L$-functions. A similar idea is used in the proof that the companions relations preserves irreducibility, which was crucial to Proposition 2.4. See also [Reference KedlayaKed18, Lemma 3.1.5, Theorem 3.3.1].
Remark 2.7 It follows from the argument of Lemma 2.5 that if ![]() $X/\mathbb {F}_q$ is smooth and geometrically connected and if
$X/\mathbb {F}_q$ is smooth and geometrically connected and if ![]() ${{\mathcal {E}}}, {{\mathcal {F}}}\in \textbf {F-Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$ are semi-simple objects, all of whose summands are algebraic, then, for any field isomorphism
${{\mathcal {E}}}, {{\mathcal {F}}}\in \textbf {F-Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$ are semi-simple objects, all of whose summands are algebraic, then, for any field isomorphism ![]() $\iota \colon \overline {\mathbb {Q}}_p\rightarrow \overline {\mathbb {Q}}_l$, we have
$\iota \colon \overline {\mathbb {Q}}_p\rightarrow \overline {\mathbb {Q}}_l$, we have ![]() $^{\iota }({{\mathcal {E}}}\otimes {{\mathcal {F}}})\cong \ ^{\iota }{{\mathcal {E}}}\otimes \ ^{\iota }{{\mathcal {F}}}$, that is, the relation of being
$^{\iota }({{\mathcal {E}}}\otimes {{\mathcal {F}}})\cong \ ^{\iota }{{\mathcal {E}}}\otimes \ ^{\iota }{{\mathcal {F}}}$, that is, the relation of being ![]() $\iota$-companions commutes with tensor product.
$\iota$-companions commutes with tensor product.
Remark 2.8 It follows from Lemma 2.5 that, in the context of Theorem 2.1, there is a decomposition
 \[ \displaystyle R^{1}(\pi_C)_*\overline{\mathbb{Q}}_l\cong \bigoplus_{i=1}^{g}(L_i) \]
\[ \displaystyle R^{1}(\pi_C)_*\overline{\mathbb{Q}}_l\cong \bigoplus_{i=1}^{g}(L_i) \]
where the ![]() $L_i$ form a complete set of
$L_i$ form a complete set of ![]() $\overline {\mathbb {Q}}_l$ companions. There are exactly
$\overline {\mathbb {Q}}_l$ companions. There are exactly ![]() $g$ non-isomorphic companions because the field generated by Frobenius traces of
$g$ non-isomorphic companions because the field generated by Frobenius traces of ![]() $L_1$ is isomorphic to
$L_1$ is isomorphic to ![]() $E$ and the
$E$ and the ![]() $l$-adic companions are in bijective correspondence with the embeddings
$l$-adic companions are in bijective correspondence with the embeddings ![]() $E\hookrightarrow \overline {\mathbb {Q}}_l$. In particular, each companion occurs with multiplicity 1. In fact, as
$E\hookrightarrow \overline {\mathbb {Q}}_l$. In particular, each companion occurs with multiplicity 1. In fact, as ![]() $E\cong \text {End}_C(A_C)\otimes {{\mathbb {Q}}}$, it follows that
$E\cong \text {End}_C(A_C)\otimes {{\mathbb {Q}}}$, it follows that ![]() $E\otimes \overline {\mathbb {Q}}_l$ acts on
$E\otimes \overline {\mathbb {Q}}_l$ acts on ![]() $R^{1}(\pi _C)_*\overline {\mathbb {Q}}_l$. On the other hand,
$R^{1}(\pi _C)_*\overline {\mathbb {Q}}_l$. On the other hand, ![]() $E\otimes \overline {\mathbb {Q}}_l\cong \prod _{i} \overline {\mathbb {Q}}_l$, where
$E\otimes \overline {\mathbb {Q}}_l\cong \prod _{i} \overline {\mathbb {Q}}_l$, where ![]() $i$ runs over the embeddings
$i$ runs over the embeddings ![]() $E\hookrightarrow \overline {\mathbb {Q}}_l$. For each
$E\hookrightarrow \overline {\mathbb {Q}}_l$. For each ![]() $i$, pick a non-trivial idempotent
$i$, pick a non-trivial idempotent ![]() $e_i\in E\otimes \overline {\mathbb {Q}}_l$ whose image is the
$e_i\in E\otimes \overline {\mathbb {Q}}_l$ whose image is the ![]() $i$th component of the direct product decomposition. The above direct sum decomposition is induced by these
$i$th component of the direct product decomposition. The above direct sum decomposition is induced by these ![]() $e_i$.
$e_i$.
To apply Drinfeld's Theorem 2.1, we will use the following lemma.
Lemma 2.9 Let ![]() $Y/\mathbb {F}_q$ be a smooth, geometrically connected, projective scheme and let
$Y/\mathbb {F}_q$ be a smooth, geometrically connected, projective scheme and let ![]() $\alpha$ be a line bundle on
$\alpha$ be a line bundle on ![]() $Y$. Let
$Y$. Let ![]() $M\subset \mathbb {P}^{m}_{\mathbb {F}_q}$ be a closed subset. Suppose there exists an infinite collection
$M\subset \mathbb {P}^{m}_{\mathbb {F}_q}$ be a closed subset. Suppose there exists an infinite collection ![]() $(C_n)_{n\in \mathbb {N}}$ of smooth, projective, geometrically connected, closed subcurves
$(C_n)_{n\in \mathbb {N}}$ of smooth, projective, geometrically connected, closed subcurves ![]() $C_n\subset Y$ such that:
$C_n\subset Y$ such that:
(1) for each
 $n\in \mathbb {N}$, the natural map
$n\in \mathbb {N}$, the natural map  $H^{0}(Y,\alpha )\rightarrow H^{0}(C_n,\alpha |_{C_n})$ is an isomorphism;
$H^{0}(Y,\alpha )\rightarrow H^{0}(C_n,\alpha |_{C_n})$ is an isomorphism;(2) for any infinite subset
 $S\subset \mathbb {N}$, the union
is Zariski dense in
$S\subset \mathbb {N}$, the union
is Zariski dense in \[ \displaystyle \bigcup_{n\in S}C_n \]
\[ \displaystyle \bigcup_{n\in S}C_n \] $Y$;
$Y$;(3) for each curve
 $C_n$, there exist
$C_n$, there exist  $m+1$ globally generating sections
such that the induced morphism to
$m+1$ globally generating sections
such that the induced morphism to \[ t_{n,0},\dots,t_{n,m}\in H^{0}(C_n,\alpha|_{C_n}) \]
\[ t_{n,0},\dots,t_{n,m}\in H^{0}(C_n,\alpha|_{C_n}) \] $\mathbb {P}^{m}$ factors through
$\mathbb {P}^{m}$ factors through  $M$:
$M$:

Then there exist global sections ![]() $\tilde {t}_0,\dots,\tilde {t}_m\in H^{0}(Y,\alpha )$ such that the induced rational map
$\tilde {t}_0,\dots,\tilde {t}_m\in H^{0}(Y,\alpha )$ such that the induced rational map ![]() $\tilde {f}\colon Y\dashrightarrow \mathbb {P}^{m}$ has image in
$\tilde {f}\colon Y\dashrightarrow \mathbb {P}^{m}$ has image in ![]() $M$. Moreover,
$M$. Moreover, ![]() $\tilde {f}$ can be chosen to be compatible with infinitely many of the maps
$\tilde {f}$ can be chosen to be compatible with infinitely many of the maps ![]() $f_n$.
$f_n$.
Proof. There are finitely many ordered ![]() $m+1$-tuples of sections
$m+1$-tuples of sections ![]() $H^{0}(Y,\alpha )\cong H^{0}(C_n,\alpha |_{C_n})$ because
$H^{0}(Y,\alpha )\cong H^{0}(C_n,\alpha |_{C_n})$ because ![]() $H^{0}(Y,\alpha )$ is a finite-dimensional vector space over
$H^{0}(Y,\alpha )$ is a finite-dimensional vector space over ![]() $\mathbb {F}_q$. By the pigeonhole principle, in our infinite collection we may find an
$\mathbb {F}_q$. By the pigeonhole principle, in our infinite collection we may find an ![]() $m+1$-tuple of sections
$m+1$-tuple of sections ![]() $\tilde {t}_0,\dots,\tilde {t}_m\in H^{0}(Y,\alpha )$ such that there exists an infinite set
$\tilde {t}_0,\dots,\tilde {t}_m\in H^{0}(Y,\alpha )$ such that there exists an infinite set ![]() $S\subset \mathbb {N}$ with
$S\subset \mathbb {N}$ with
for every ![]() $n\in S$. There is therefore an induced rational map
$n\in S$. There is therefore an induced rational map ![]() $\tilde {f}\colon Y\dashrightarrow \mathbb {P}^{m}$ with
$\tilde {f}\colon Y\dashrightarrow \mathbb {P}^{m}$ with ![]() $\tilde {f}|_{C_n}=f_n$ for each
$\tilde {f}|_{C_n}=f_n$ for each ![]() $n\in S$. On the other hand, the collection
$n\in S$. On the other hand, the collection ![]() $(C_n)_{n\in S}$ is Zariski dense in
$(C_n)_{n\in S}$ is Zariski dense in ![]() $Y$ by assumption and
$Y$ by assumption and ![]() $\tilde {f}(C_n)\subset M$; therefore the image of
$\tilde {f}(C_n)\subset M$; therefore the image of ![]() $\tilde {f}$ lands inside of
$\tilde {f}$ lands inside of ![]() $M$, as desired.
$M$, as desired.
Lemma 2.9 has two key ingredients. The first ingredient is that if ![]() $X/\mathbb {F}_q$ is a projective variety and
$X/\mathbb {F}_q$ is a projective variety and ![]() $\alpha$ is a coherent sheaf on
$\alpha$ is a coherent sheaf on ![]() $X$, then
$X$, then ![]() $H^{0}(X,\alpha )$ is a finite set. The second ingredient is the pigeonhole principle. To use Lemma 2.9, the following definition will be useful.
$H^{0}(X,\alpha )$ is a finite set. The second ingredient is the pigeonhole principle. To use Lemma 2.9, the following definition will be useful.
Definition 2.10 Let ![]() $\bar {X}/k$ be a smooth, geometrically connected, projective scheme of dimension at least 2, let
$\bar {X}/k$ be a smooth, geometrically connected, projective scheme of dimension at least 2, let ![]() $Z\subset \bar {X}$ be a reduced simple normal crossings divisor, and set
$Z\subset \bar {X}$ be a reduced simple normal crossings divisor, and set ![]() $X:=X\backslash Z$. Let
$X:=X\backslash Z$. Let ![]() $\bar {U}\subset \bar {X}$ be an open subset whose complement has codimension at least 2. Let
$\bar {U}\subset \bar {X}$ be an open subset whose complement has codimension at least 2. Let ![]() $(x_j)_{j=1}^{s}$ be a finite collection of closed points of
$(x_j)_{j=1}^{s}$ be a finite collection of closed points of ![]() $U:=\bar {U}\cap X$. Let
$U:=\bar {U}\cap X$. Let ![]() $\alpha$ be a line bundle on
$\alpha$ be a line bundle on ![]() $\bar {X}$. We say that
$\bar {X}$. We say that ![]() $\bar {C}\subset \bar {U}$ is a good curve for the quintuple
$\bar {C}\subset \bar {U}$ is a good curve for the quintuple ![]() $(\bar {X}, X, \bar {U}, \alpha, (x_j)^{s}_{j=1})$ if:
$(\bar {X}, X, \bar {U}, \alpha, (x_j)^{s}_{j=1})$ if:
•
 $\bar {C}$ is the smooth complete intersection of smooth ample divisors of
$\bar {C}$ is the smooth complete intersection of smooth ample divisors of  $\bar {X}$ that intersect
$\bar {X}$ that intersect  $Z$ in good position;
$Z$ in good position;•
 $\bar {C}$ contains each of the closed points
$\bar {C}$ contains each of the closed points  $x_j$, for
$x_j$, for  $j=1,\dots, s$;
$j=1,\dots, s$;• the natural map
 $H^{0}(\bar {X},\alpha )\rightarrow H^{0}(\bar {C},\alpha |_{\bar {C}})$ is an isomorphism.
$H^{0}(\bar {X},\alpha )\rightarrow H^{0}(\bar {C},\alpha |_{\bar {C}})$ is an isomorphism.
In the proof of Theorem 1.2, we will need to know that good curves exist. This is guaranteed by the following two results.
Proposition 2.11 Let ![]() $Y/k$ be a smooth, geometrically connected, projective scheme of dimension
$Y/k$ be a smooth, geometrically connected, projective scheme of dimension ![]() $d\geq 2$ and let
$d\geq 2$ and let ![]() $\alpha$ be a line bundle on
$\alpha$ be a line bundle on ![]() $Y$. Let
$Y$. Let ![]() $D\subset Y$ be an ample divisor. Then there exists an
$D\subset Y$ be an ample divisor. Then there exists an ![]() $s_0>0$ such that, for any
$s_0>0$ such that, for any ![]() $s\geq s_0$, and for any integral divisor
$s\geq s_0$, and for any integral divisor ![]() $E\in |sD|$ in the linear series, the natural map
$E\in |sD|$ in the linear series, the natural map
is an isomorphism.
Proof. For any ![]() $s>0$, let
$s>0$, let ![]() $E\in |sD|$ be an integral divisor in the linear series. Then there is an exact sequence
$E\in |sD|$ be an integral divisor in the linear series. Then there is an exact sequence
If ![]() $h^{0}(Y,\alpha (-E))=h^{1}(Y,\alpha (-E))=0$, then by the long exact sequence in cohomology, the restriction map
$h^{0}(Y,\alpha (-E))=h^{1}(Y,\alpha (-E))=0$, then by the long exact sequence in cohomology, the restriction map ![]() $H^{0}(Y,\alpha )\rightarrow H^{0}(E,\alpha |_E)$ is an isomorphism. Our task is therefore to show that, for all sufficiently large
$H^{0}(Y,\alpha )\rightarrow H^{0}(E,\alpha |_E)$ is an isomorphism. Our task is therefore to show that, for all sufficiently large ![]() $s$,
$s$, ![]() $h^{0}(Y,\alpha (-sD))=h^{1}(Y,\alpha (-sD))=0$.
$h^{0}(Y,\alpha (-sD))=h^{1}(Y,\alpha (-sD))=0$.
Let ![]() $\mathfrak {L}$ be the canonical bundle of
$\mathfrak {L}$ be the canonical bundle of ![]() $Y$. Then by Serre duality,
$Y$. Then by Serre duality, ![]() $h^{i}(Y,\alpha (-sD))=h^{d-i}(Y,\alpha ^{\vee }(sD)\otimes \mathfrak {L})$. It follows from Serre vanishing that there exists an
$h^{i}(Y,\alpha (-sD))=h^{d-i}(Y,\alpha ^{\vee }(sD)\otimes \mathfrak {L})$. It follows from Serre vanishing that there exists an ![]() $s_0>0$ such that, for any
$s_0>0$ such that, for any ![]() $s\geq s_0$ and for any
$s\geq s_0$ and for any ![]() $i< d$,
$i< d$, ![]() $h^{d-i}(Y,\alpha ^{\vee }(sD)\otimes \mathfrak {L})=0$. Therefore, for any
$h^{d-i}(Y,\alpha ^{\vee }(sD)\otimes \mathfrak {L})=0$. Therefore, for any ![]() $s\geq s_0$ and for any
$s\geq s_0$ and for any ![]() $i< d$,
$i< d$, ![]() $h^{i}(Y,\alpha (-sD))=0$ and the result follows.
$h^{i}(Y,\alpha (-sD))=0$ and the result follows.
Lemma 2.12 Let ![]() $\bar {X}/\mathbb {F}_q$ be a smooth, geometrically connected, projective scheme of dimension at least
$\bar {X}/\mathbb {F}_q$ be a smooth, geometrically connected, projective scheme of dimension at least ![]() $2$, let
$2$, let ![]() $Z\subset \bar {X}$ be a reduced simple normal crossings divisor, and set
$Z\subset \bar {X}$ be a reduced simple normal crossings divisor, and set ![]() $X:=\bar {X}\backslash Z$. Let
$X:=\bar {X}\backslash Z$. Let ![]() $\bar {U}\subset \bar {X}$ be an open subset whose complement has codimension at least
$\bar {U}\subset \bar {X}$ be an open subset whose complement has codimension at least ![]() $2$. Let
$2$. Let ![]() $(x_j)_{j=1}^{s}$ be a finite collection of closed points of
$(x_j)_{j=1}^{s}$ be a finite collection of closed points of ![]() $U:=\bar {U}\cap X$. Let
$U:=\bar {U}\cap X$. Let ![]() $\alpha$ be a line bundle on
$\alpha$ be a line bundle on ![]() $\bar {X}$. Then there is a good curve
$\bar {X}$. Then there is a good curve ![]() $\bar {C}\subset \bar {U}$ for the quintuple
$\bar {C}\subset \bar {U}$ for the quintuple ![]() $(\bar {X}, X, \bar {U}, \alpha, (x_j)^{s}_{j=1})$
$(\bar {X}, X, \bar {U}, \alpha, (x_j)^{s}_{j=1})$
Proof. By induction, it suffices to construct a smooth ample divisor ![]() $\bar {D}\subset \bar {X}$ such that:
$\bar {D}\subset \bar {X}$ such that:
•
 $\bar {D}\cap \bar {U}$ has complementary codimension at least
$\bar {D}\cap \bar {U}$ has complementary codimension at least  $2$ in
$2$ in  $\bar {D}$;
$\bar {D}$;•
 $\bar {D}$ intersects
$\bar {D}$ intersects  $Z$ transversely;
$Z$ transversely;•
 $\bar {D}$ contains
$\bar {D}$ contains  $x_j$, for
$x_j$, for  $j=1,\dots, s$; and
$j=1,\dots, s$; and• the natural map
 $H^{0}(\bar {X},\alpha )\rightarrow H^{0}(\bar {D},\alpha |_{\bar {D}})$ is an isomorphism.
$H^{0}(\bar {X},\alpha )\rightarrow H^{0}(\bar {D},\alpha |_{\bar {D}})$ is an isomorphism.
This is a standard application of Poonen's Bertini theorem over finite fields [Reference PoonenPoo04, Theorem 1.3]. Fix a closed embedding ![]() $\bar {X}\hookrightarrow \mathbb {P}^{m}_{\mathbb {F}_q}$ and let
$\bar {X}\hookrightarrow \mathbb {P}^{m}_{\mathbb {F}_q}$ and let ![]() $S_{\text {homog}}$ be the set of homogenous polynomials on
$S_{\text {homog}}$ be the set of homogenous polynomials on ![]() $\mathbb {P}^{m}_{\mathbb {F}_q}$, as in [Reference PoonenPoo04, p. 1100]. Consider the set
$\mathbb {P}^{m}_{\mathbb {F}_q}$, as in [Reference PoonenPoo04, p. 1100]. Consider the set ![]() $\mathcal {T}$ of those functions
$\mathcal {T}$ of those functions ![]() $f\in S_{\text {homog}}$ such that
$f\in S_{\text {homog}}$ such that ![]() $\bar {D}:=V(f)\cap \bar {X}$ is a smooth ample divisor of
$\bar {D}:=V(f)\cap \bar {X}$ is a smooth ample divisor of ![]() $\bar {X}$ and the above four properties hold for
$\bar {X}$ and the above four properties hold for ![]() $\bar {D}$. Our goal is to show that
$\bar {D}$. Our goal is to show that ![]() $\mathcal {T}$ is non-empty.
$\mathcal {T}$ is non-empty.
• Let
 $\bar E:=\bar {X}{\setminus} \bar {U}$; by hypothesis,
$\bar E:=\bar {X}{\setminus} \bar {U}$; by hypothesis,  $\dim (\bar E)\leq n-2$. If
$\dim (\bar E)\leq n-2$. If  $f\in S_{\text {homog}}$ is such that
$f\in S_{\text {homog}}$ is such that  $V(f)$ does not contain any component of
$V(f)$ does not contain any component of  $\bar E$, then
$\bar E$, then  $\dim (V(f)\cap \bar E)\leq n-3$. For this to hold, it is sufficient that
$\dim (V(f)\cap \bar E)\leq n-3$. For this to hold, it is sufficient that  $V(f)$ avoids at least one given closed point
$V(f)$ avoids at least one given closed point  $e_i$ on each connected component of
$e_i$ on each connected component of  $\bar E$.
$\bar E$.• Write
 $Z=\bigcup ^{r}_{j=1} Z_j$ to be the decomposition of
$Z=\bigcup ^{r}_{j=1} Z_j$ to be the decomposition of  $Z$ into connected components. For each
$Z$ into connected components. For each  $J\subset \{1,2,\dots,r\}$, set
$J\subset \{1,2,\dots,r\}$, set  $Z_J:=\bigcap _{j\in J}Z_j$ to be the corresponding scheme-theoretic intersection. By assumption, for each
$Z_J:=\bigcap _{j\in J}Z_j$ to be the corresponding scheme-theoretic intersection. By assumption, for each  $J$,
$J$,  $Z_J$ is a smooth subvariety of
$Z_J$ is a smooth subvariety of  $\bar {X}$. The condition that
$\bar {X}$. The condition that  $\bar {D}$ intersects
$\bar {D}$ intersects  $Z$ in good position means that
$Z$ in good position means that  $\bar {D}$ must intersect each stratum
$\bar {D}$ must intersect each stratum  $Z_J$ transversely, that is, that
$Z_J$ transversely, that is, that  $Z_J\cap \bar {D}$ is a smooth subvariety of
$Z_J\cap \bar {D}$ is a smooth subvariety of  $\bar {D}$ of dimension
$\bar {D}$ of dimension  $n-1-|J|$.
$n-1-|J|$.
Then the positive density (and hence non-emptiness) of ![]() $\mathcal {T}$ immediately follows from [Reference PoonenPoo04, Theorem 1.3]: the conditions on
$\mathcal {T}$ immediately follows from [Reference PoonenPoo04, Theorem 1.3]: the conditions on ![]() $f$ are that
$f$ are that ![]() $V(f)\cap \bar {X}$ intersect a finite set of smooth subvarieties transversely, avoid a given finite set of points, pass through another given finite set of points, and have sufficiently high degree by Proposition 2.11.
$V(f)\cap \bar {X}$ intersect a finite set of smooth subvarieties transversely, avoid a given finite set of points, pass through another given finite set of points, and have sufficiently high degree by Proposition 2.11.
Note that Lemma 2.12 also holds with ![]() $\mathbb {F}_q$ replaced by any infinite field
$\mathbb {F}_q$ replaced by any infinite field ![]() $k$ by the usual Bertini theorems. Finally, the following lemma is surely well known but we could not find a reference for exactly the statement we need. (The essential content is contained in [Reference Chai, Conrad and OortCCO14, § 3.3].) We will use this lemma to make a particular choice of
$k$ by the usual Bertini theorems. Finally, the following lemma is surely well known but we could not find a reference for exactly the statement we need. (The essential content is contained in [Reference Chai, Conrad and OortCCO14, § 3.3].) We will use this lemma to make a particular choice of ![]() $A_C\rightarrow C$ in the isogeny class from Drinfeld's Theorem 2.1 (though this choice will not be unique).
$A_C\rightarrow C$ in the isogeny class from Drinfeld's Theorem 2.1 (though this choice will not be unique).
Lemma 2.13 Let ![]() $X$ be a scheme and let
$X$ be a scheme and let ![]() $A\rightarrow X$ be an abelian scheme. Let
$A\rightarrow X$ be an abelian scheme. Let ![]() $r$ be a prime and let
$r$ be a prime and let ![]() $G$ be an
$G$ be an ![]() $r$-divisible group on
$r$-divisible group on ![]() $X$. Suppose there exists an isogeny
$X$. Suppose there exists an isogeny ![]() $\psi \colon A[r^{\infty }]\rightarrow G$ of
$\psi \colon A[r^{\infty }]\rightarrow G$ of ![]() $r$-divisible groups on
$r$-divisible groups on ![]() $X$ (as in [Reference Chai, Conrad and OortCCO14, 3.3.5]). Then there exist an
$X$ (as in [Reference Chai, Conrad and OortCCO14, 3.3.5]). Then there exist an ![]() $r$-primary isogeny
$r$-primary isogeny ![]() $\varphi \colon A\rightarrow B$ of abelian schemes over
$\varphi \colon A\rightarrow B$ of abelian schemes over ![]() $X$ and an isomorphism
$X$ and an isomorphism ![]() $\varepsilon \colon B[r^{\infty }]\rightarrow G$ such that the following diagram commutes:
$\varepsilon \colon B[r^{\infty }]\rightarrow G$ such that the following diagram commutes:

Proof. Set ![]() $N=\text {ker}(\psi )$. Then
$N=\text {ker}(\psi )$. Then ![]() $N$ is a (commutative) finite flat group scheme over
$N$ is a (commutative) finite flat group scheme over ![]() $X$ of
$X$ of ![]() $r$-primary order. We have a short exact sequence in the category of fppf sheaves:
$r$-primary order. We have a short exact sequence in the category of fppf sheaves:
Consider the quotient ![]() $A/N$ in the category of fppf sheaves. It follows from, for example, [Reference Chai, Conrad and OortCCO14, 1.4.1.3, 1.4.1.4] that there exists an abelian scheme
$A/N$ in the category of fppf sheaves. It follows from, for example, [Reference Chai, Conrad and OortCCO14, 1.4.1.3, 1.4.1.4] that there exists an abelian scheme ![]() $B\rightarrow X$ that represents the sheaf
$B\rightarrow X$ that represents the sheaf ![]() $A/N$. We then have the following commutative diagram of fppf sheaves:
$A/N$. We then have the following commutative diagram of fppf sheaves:

where the right vertical arrow exists because ![]() $G=\text {coker}(N\rightarrow A[r^{\infty }])$. We claim that the induced map
$G=\text {coker}(N\rightarrow A[r^{\infty }])$. We claim that the induced map ![]() $G\rightarrow B$ yields an isomorphism
$G\rightarrow B$ yields an isomorphism ![]() $G\rightarrow B[r^{\infty }]$. By the snake lemma,
$G\rightarrow B[r^{\infty }]$. By the snake lemma, ![]() $G\rightarrow B$ is injective. However, an injective isogeny of
$G\rightarrow B$ is injective. However, an injective isogeny of ![]() $r$-divisible groups is an isomorphism.
$r$-divisible groups is an isomorphism.
3. Proofs of Theorem 1.2 and Corollaries 1.3, 1.4
Proof of Theorem 1.2 We proceed in several steps.
Step 1: organizing the summands of ![]() $\mathcal {E}$. As
$\mathcal {E}$. As ![]() ${{\mathcal {E}}}_i$ is irreducible, has determinant
${{\mathcal {E}}}_i$ is irreducible, has determinant ![]() $\overline {\mathbb {Q}}_p(-1)$, and has rank
$\overline {\mathbb {Q}}_p(-1)$, and has rank ![]() $2$, the slopes of
$2$, the slopes of ![]() $({{\mathcal {E}}}_i)_x$ are in the interval
$({{\mathcal {E}}}_i)_x$ are in the interval ![]() $[0,1]$ for every closed point
$[0,1]$ for every closed point ![]() $x$ of
$x$ of ![]() $X$ (see [Reference Drinfeld and KedlayaDK17, § 1.2, pp. 136–137], where it is deduced from Corollary 1.1.7).
$X$ (see [Reference Drinfeld and KedlayaDK17, § 1.2, pp. 136–137], where it is deduced from Corollary 1.1.7).
Write the isotypic decomposition of ![]() ${{\mathcal {E}}}$ in
${{\mathcal {E}}}$ in ![]() $\textbf {F-Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$:
$\textbf {F-Isoc}^{{\dagger} }({X})_{\overline {\mathbb {Q}}_p}$:
 \[ \displaystyle {{\mathcal{E}}}\cong \bigoplus_{i=1}^{a}({{\mathcal{E}}}_i)^{m_i}. \]
\[ \displaystyle {{\mathcal{E}}}\cong \bigoplus_{i=1}^{a}({{\mathcal{E}}}_i)^{m_i}. \] The field generated by the coefficients of ![]() $P_x({{\mathcal {E}}},t)$ as
$P_x({{\mathcal {E}}},t)$ as ![]() $x$ ranges through closed points of
$x$ ranges through closed points of ![]() $X$ is
$X$ is ![]() ${{\mathbb {Q}}}$. Therefore, by [Reference DrinfeldDri18, E.10] and either [Reference Abe and EsnaultAE19, Theorem 4.2] or [Reference KedlayaKed18, Corollary 3.5.3], we can pick an
${{\mathbb {Q}}}$. Therefore, by [Reference DrinfeldDri18, E.10] and either [Reference Abe and EsnaultAE19, Theorem 4.2] or [Reference KedlayaKed18, Corollary 3.5.3], we can pick an ![]() $l$ and a field isomorphism
$l$ and a field isomorphism ![]() $\sigma \colon \overline {\mathbb {Q}}_p\rightarrow \overline {\mathbb {Q}}_l$ such that the semi-simple
$\sigma \colon \overline {\mathbb {Q}}_p\rightarrow \overline {\mathbb {Q}}_l$ such that the semi-simple ![]() $\sigma$ companion
$\sigma$ companion ![]() $L$ to
$L$ to ![]() ${{\mathcal {E}}}$ exists and in fact may be defined over
${{\mathcal {E}}}$ exists and in fact may be defined over ![]() $\mathbb {Q}_l$, that is, corresponds to a representation
$\mathbb {Q}_l$, that is, corresponds to a representation
(We emphasize that ![]() $L$ is independent of the choice of
$L$ is independent of the choice of ![]() $\sigma$ by Proposition 2.4.) By compactness of
$\sigma$ by Proposition 2.4.) By compactness of ![]() $\pi _1(X)$, we may conjugate the representation into
$\pi _1(X)$, we may conjugate the representation into ![]() $\mathrm {GL}_N({{\mathbb {Z}}}_l)$. We refer to the attached lisse
$\mathrm {GL}_N({{\mathbb {Z}}}_l)$. We refer to the attached lisse ![]() ${{\mathbb {Z}}}_l$-sheaf as
${{\mathbb {Z}}}_l$-sheaf as ![]() $\tilde {L}$. Similarly, for each
$\tilde {L}$. Similarly, for each ![]() $i$ we denote by
$i$ we denote by ![]() $L_i$ the
$L_i$ the ![]() $\sigma$-companion to
$\sigma$-companion to ![]() ${{\mathcal {E}}}_i$ (the
${{\mathcal {E}}}_i$ (the ![]() $L_i$ indeed do depend on the choice of
$L_i$ indeed do depend on the choice of ![]() $\sigma$). The companion relation commutes with direct sum; hence, we have
$\sigma$). The companion relation commutes with direct sum; hence, we have
 \[ \displaystyle L\cong \bigoplus_{i=1}^{a} L_i^{m_i}. \]
\[ \displaystyle L\cong \bigoplus_{i=1}^{a} L_i^{m_i}. \]
(See also the proof of Proposition 2.4.) Let ![]() $E_i\subset \overline {\mathbb {Q}}_p$ denote the (number) field generated by the coefficients of
$E_i\subset \overline {\mathbb {Q}}_p$ denote the (number) field generated by the coefficients of ![]() $P_x({{\mathcal {E}}}_i,t)$ as
$P_x({{\mathcal {E}}}_i,t)$ as ![]() $x$ ranges through the closed points of
$x$ ranges through the closed points of ![]() $X$. Note that for each
$X$. Note that for each ![]() ${{\mathcal {E}}}_i$, all
${{\mathcal {E}}}_i$, all ![]() $p$-adic companions exist and are summands of
$p$-adic companions exist and are summands of ![]() ${{\mathcal {E}}}$ by Lemma 2.5. For each
${{\mathcal {E}}}$ by Lemma 2.5. For each ![]() ${{\mathcal {E}}}_i$, set
${{\mathcal {E}}}_i$, set ![]() ${{\mathcal {F}}}_i$ to be the sum of all distinct
${{\mathcal {F}}}_i$ to be the sum of all distinct ![]() $p$-adic companions of
$p$-adic companions of ![]() ${{\mathcal {E}}}_i$. Note that there are
${{\mathcal {E}}}_i$. Note that there are ![]() $[E_i\colon {{\mathbb {Q}}}]$ distinct
$[E_i\colon {{\mathbb {Q}}}]$ distinct ![]() $p$-adic companions of
$p$-adic companions of ![]() ${{\mathcal {E}}}_i$, parametrized by the embeddings
${{\mathcal {E}}}_i$, parametrized by the embeddings ![]() $E_i\hookrightarrow \overline {\mathbb {Q}}_p$. By reordering the indices, we write the decomposition of
$E_i\hookrightarrow \overline {\mathbb {Q}}_p$. By reordering the indices, we write the decomposition of ![]() ${{\mathcal {E}}}$ as
${{\mathcal {E}}}$ as
 \begin{equation} \displaystyle {{\mathcal{E}}}\cong \bigoplus_{i=1}^{b} {{\mathcal{F}}}_i^{m_i} \end{equation}
\begin{equation} \displaystyle {{\mathcal{E}}}\cong \bigoplus_{i=1}^{b} {{\mathcal{F}}}_i^{m_i} \end{equation}
for some integer ![]() $1\leq b\leq a$. (Under this reordering, the collection of
$1\leq b\leq a$. (Under this reordering, the collection of ![]() $({{\mathcal {E}}}_i)_{i=1}^{b}$ are all mutually not companions and, for each
$({{\mathcal {E}}}_i)_{i=1}^{b}$ are all mutually not companions and, for each ![]() $b+1\leq j \leq a$, there exists a unique
$b+1\leq j \leq a$, there exists a unique ![]() $1\leq i\leq b$ such that
$1\leq i\leq b$ such that ![]() ${{\mathcal {E}}}_j$ is a companion of
${{\mathcal {E}}}_j$ is a companion of ![]() ${{\mathcal {E}}}_i$.) Set
${{\mathcal {E}}}_i$.) Set
 \begin{equation} g=\sum_{j=1}^{b} m_i[E_i\colon {{\mathbb{Q}}}].\end{equation}
\begin{equation} g=\sum_{j=1}^{b} m_i[E_i\colon {{\mathbb{Q}}}].\end{equation} Step 2: the proof in a simplified situation. We first assume that ![]() $X$ admits a simple normal crossings compactification
$X$ admits a simple normal crossings compactification ![]() $\bar {X}$ such that
$\bar {X}$ such that ![]() ${{\mathcal {E}}}$ extends to a logarithmic
${{\mathcal {E}}}$ extends to a logarithmic ![]() $F$-isocrystal
$F$-isocrystal ![]() $\bar {{\mathcal {E}}}$ with nilpotent residues on
$\bar {{\mathcal {E}}}$ with nilpotent residues on ![]() $\bar {X}$ and, moreover, that
$\bar {X}$ and, moreover, that ![]() $\tilde {L}$ has trivial residual representation. Write
$\tilde {L}$ has trivial residual representation. Write ![]() $Z:=\bar {X}\backslash X$ for the boundary. (Note that under the above assumption on
$Z:=\bar {X}\backslash X$ for the boundary. (Note that under the above assumption on ![]() ${{\mathcal {E}}}$, the
${{\mathcal {E}}}$, the ![]() $l$-companion
$l$-companion ![]() $L$ is tamely ramified.)
$L$ is tamely ramified.)
By Lemma A.7, there exist a Zariski open ![]() $\bar {U}\subset \bar {X}$ with complementary codimension at least 2, and a logarithmic Dieudonné crystal
$\bar {U}\subset \bar {X}$ with complementary codimension at least 2, and a logarithmic Dieudonné crystal ![]() $(M_{\bar {U}},F,V)$ on
$(M_{\bar {U}},F,V)$ on ![]() $\bar {U}$ (with the logarithmic structure coming from
$\bar {U}$ (with the logarithmic structure coming from ![]() $Z\cap \bar {U}$) such that the associated logarithmic
$Z\cap \bar {U}$) such that the associated logarithmic ![]() $F$-isocrystal is isomorphic to
$F$-isocrystal is isomorphic to ![]() $\overline {{{\mathcal {E}}}}|_{\bar {U}}$. (In other words,
$\overline {{{\mathcal {E}}}}|_{\bar {U}}$. (In other words, ![]() $M_{\bar {U}}$ is an
$M_{\bar {U}}$ is an ![]() $F$ and
$F$ and ![]() $p\circ F^{-1}$ stable lattice in
$p\circ F^{-1}$ stable lattice in ![]() $\overline {{{\mathcal {E}}}}|_{\bar {U}}$.) Let
$\overline {{{\mathcal {E}}}}|_{\bar {U}}$.) Let
where the ![]() $t$ denotes the dual logarithmic Dieudonné crystal. We also consider this logarithmic Dieudonné crystal as we will need to use Zarhin's trick. We set
$t$ denotes the dual logarithmic Dieudonné crystal. We also consider this logarithmic Dieudonné crystal as we will need to use Zarhin's trick. We set ![]() $U:=\bar {U}\backslash (\bar {U}\cap Z)$.
$U:=\bar {U}\backslash (\bar {U}\cap Z)$.
After Remark A.8, it follows that we may define Hodge line bundles ![]() $\omega _M$ and
$\omega _M$ and ![]() $\omega _N$ on
$\omega _N$ on ![]() $\bar {U}$ attached to the two logarithmic Dieudonné crystals. As
$\bar {U}$ attached to the two logarithmic Dieudonné crystals. As ![]() $\bar {U}\subset \bar {X}$ has complementary codimension at least
$\bar {U}\subset \bar {X}$ has complementary codimension at least ![]() $2$ and
$2$ and ![]() $\bar {X}$ is smooth, it follows that
$\bar {X}$ is smooth, it follows that ![]() $\omega _M$ and
$\omega _M$ and ![]() $\omega _N$ extend canonically to line bundles on all of
$\omega _N$ extend canonically to line bundles on all of ![]() $\bar {X}$.
$\bar {X}$.
The Hodge line bundle ![]() $\alpha$ on the fine moduli scheme
$\alpha$ on the fine moduli scheme ![]() $\mathscr {A}_{8g,1,l}\otimes \mathbb {F}_q$ is ample by [Reference Moret-BaillyMB85, Ch. IX, Théorème 3.1, p. 210] or [Reference Faltings and ChaiFC90, Ch. V, Theorem 2.5(i)]. Let
$\mathscr {A}_{8g,1,l}\otimes \mathbb {F}_q$ is ample by [Reference Moret-BaillyMB85, Ch. IX, Théorème 3.1, p. 210] or [Reference Faltings and ChaiFC90, Ch. V, Theorem 2.5(i)]. Let ![]() $g$ be as in (3.2) and choose an
$g$ be as in (3.2) and choose an ![]() $r$ so that the
$r$ so that the ![]() $\alpha ^{r}$ is very ample on
$\alpha ^{r}$ is very ample on ![]() $\mathscr {A}_{8g,1,l}$. As
$\mathscr {A}_{8g,1,l}$. As ![]() $8g>1$, it follows from the Koecher principle that
$8g>1$, it follows from the Koecher principle that ![]() $H^{0}(\mathscr {A}_{8g,1,l}\otimes \mathbb {F}_q,\alpha ^{r})$ is a finite-dimensional
$H^{0}(\mathscr {A}_{8g,1,l}\otimes \mathbb {F}_q,\alpha ^{r})$ is a finite-dimensional ![]() $\mathbb {F}_q$-vector space for all
$\mathbb {F}_q$-vector space for all ![]() $r\in \mathbb {Z}$ [Reference Faltings and ChaiFC90, Ch. V, Theorem 1.5(ii)]. Fix a basis
$r\in \mathbb {Z}$ [Reference Faltings and ChaiFC90, Ch. V, Theorem 1.5(ii)]. Fix a basis ![]() $s_0,\dots,s_m$ of the vector space
$s_0,\dots,s_m$ of the vector space
once and for all. There is an induced embedding ![]() $\mathscr {A}_{8g,1,l}\subset \mathbb {P}^{m}$. As is customary, denote by
$\mathscr {A}_{8g,1,l}\subset \mathbb {P}^{m}$. As is customary, denote by ![]() $\mathscr {A}^{*}_{8g,1,l}$ the Zariski closure of
$\mathscr {A}^{*}_{8g,1,l}$ the Zariski closure of ![]() $\mathscr {A}_{8g,1,l}$ in
$\mathscr {A}_{8g,1,l}$ in ![]() $\mathbb {P}^{m}$; we call this the minimal compactification. In an abuse of notation, we also denote by
$\mathbb {P}^{m}$; we call this the minimal compactification. In an abuse of notation, we also denote by ![]() $\alpha$ the Hodge line bundle on
$\alpha$ the Hodge line bundle on ![]() $\mathscr {A}^{*}_{8g,1,l}$. The Koecher principle implies that
$\mathscr {A}^{*}_{8g,1,l}$. The Koecher principle implies that ![]() $H^{0}(\mathscr {A}_{8g,1,l}\otimes \mathbb {F}_q,\alpha ^{r})=H^{0}(\mathscr {A}^{*}_{8g,1,l}\otimes \mathbb {F}_q,\alpha ^{r})$; this follows from [Reference Faltings and ChaiFC90, Ch. V, Theorem 1.5(ii), Theorem 2.5(iii)].
$H^{0}(\mathscr {A}_{8g,1,l}\otimes \mathbb {F}_q,\alpha ^{r})=H^{0}(\mathscr {A}^{*}_{8g,1,l}\otimes \mathbb {F}_q,\alpha ^{r})$; this follows from [Reference Faltings and ChaiFC90, Ch. V, Theorem 1.5(ii), Theorem 2.5(iii)].
It follows from [Reference DeligneDel12, Proposition 3.4] that there exist a finite number of closed points ![]() $(x_j)^{s}_{j=1}$ of
$(x_j)^{s}_{j=1}$ of ![]() $U$ such that, for each
$U$ such that, for each ![]() ${{\mathcal {E}}}_i$, the field generated by the coefficients of
${{\mathcal {E}}}_i$, the field generated by the coefficients of ![]() $P_{x_j}({{\mathcal {E}}}_i,t)\in \overline {\mathbb {Q}}_p[t]$ as
$P_{x_j}({{\mathcal {E}}}_i,t)\in \overline {\mathbb {Q}}_p[t]$ as ![]() $j=1,\dots, s$ is
$j=1,\dots, s$ is ![]() $E_i\subset \overline {\mathbb {Q}}_p$. We call this fact
$E_i\subset \overline {\mathbb {Q}}_p$. We call this fact ![]() $\blacklozenge$.
$\blacklozenge$.
If ![]() $\bar {C}\subset \bar {U}$ is a good curve for the quintuple
$\bar {C}\subset \bar {U}$ is a good curve for the quintuple ![]() $(\bar {X}, X, \bar {U}, \omega _N^{r}, (x_j)^{s}_{j=1})$ as in Definition 2.10, set
$(\bar {X}, X, \bar {U}, \omega _N^{r}, (x_j)^{s}_{j=1})$ as in Definition 2.10, set ![]() $C:=\bar {C}\cap X$. Then the following three properties hold.
$C:=\bar {C}\cap X$. Then the following three properties hold.
• Each
 ${{\mathcal {E}}}_i|_C$ is irreducible by [Reference Abe and EsnaultAE19, Theorem 2.6].
${{\mathcal {E}}}_i|_C$ is irreducible by [Reference Abe and EsnaultAE19, Theorem 2.6].• The field generated by Frobenius traces of
 ${{\mathcal {E}}}_i|_C$ is
${{\mathcal {E}}}_i|_C$ is  $E_i$ by
$E_i$ by  $\blacklozenge$.
$\blacklozenge$.• Each
 ${{\mathcal {E}}}_i|_C$ has infinite monodromy around
${{\mathcal {E}}}_i|_C$ has infinite monodromy around  $\infty$. Indeed, from the positivity of
$\infty$. Indeed, from the positivity of  $\bar {C}$, and the good position assumption, it follows that
$\bar {C}$, and the good position assumption, it follows that  $\bar {C}$ intersects each irreducible component
$\bar {C}$ intersects each irreducible component  $Z_m$ of
$Z_m$ of  $Z$ in a non-empty and transverse way; moreover,
$Z$ in a non-empty and transverse way; moreover,  $\bar {C}$ does not intersect the codimension
$\bar {C}$ does not intersect the codimension  $2$ strata
$2$ strata  $Z_{m}\cap Z_n$. By assumption, for each
$Z_{m}\cap Z_n$. By assumption, for each  ${{\mathcal {E}}}_i$, there exists a component
${{\mathcal {E}}}_i$, there exists a component  $Z_m$ around which the monodromy around
$Z_m$ around which the monodromy around  $Z_m$ of
$Z_m$ of  ${{\mathcal {E}}}_i$ (equivalently, of
${{\mathcal {E}}}_i$ (equivalently, of  $L_i$) is infinite. On the other hand, there is a surjective morphism of tame fundamental groups
by [Reference Esnault and KindlerEK16, Theorem 1.1(a)]. Moreover, for each
$L_i$) is infinite. On the other hand, there is a surjective morphism of tame fundamental groups
by [Reference Esnault and KindlerEK16, Theorem 1.1(a)]. Moreover, for each \[ \pi_1^{\text{tame}}(C)\twoheadrightarrow \pi_1^{\text{tame}}(X) \]
\[ \pi_1^{\text{tame}}(C)\twoheadrightarrow \pi_1^{\text{tame}}(X) \] $m$, we may restrict the above surjection to a surjective map of tame inertia groups
around
$m$, we may restrict the above surjection to a surjective map of tame inertia groups
around \[ I_{Z_m\cap \bar{C}}^{\text{tame}}(C)\twoheadrightarrow I_{Z_m}^{\text{tame}}(X) \]
\[ I_{Z_m\cap \bar{C}}^{\text{tame}}(C)\twoheadrightarrow I_{Z_m}^{\text{tame}}(X) \] $Z_m\cap \bar {C}$ and
$Z_m\cap \bar {C}$ and  $Z_m$, respectively. By the assumption that
$Z_m$, respectively. By the assumption that  $L_i$ had infinite monodromy around
$L_i$ had infinite monodromy around  $Z_m$ and the fact that wild inertia is a pro-
$Z_m$ and the fact that wild inertia is a pro- $p$ group, it follows that the image of
$p$ group, it follows that the image of  $I_{Z_m}^{\text {tame}}(X)$ in the
$I_{Z_m}^{\text {tame}}(X)$ in the  $l$-adic representation corresponding to
$l$-adic representation corresponding to  $L_i$ is infinite. Therefore, the image of
$L_i$ is infinite. Therefore, the image of  $I_{Z_m\cap \bar {C}}^{\text {tame}}(C)$ in the
$I_{Z_m\cap \bar {C}}^{\text {tame}}(C)$ in the  $l$-adic representation corresponding to
$l$-adic representation corresponding to  $L_i|_C$ is also infinite, or equivalently,
$L_i|_C$ is also infinite, or equivalently,  ${{\mathcal {E}}}_i|_C$ has infinite monodromy around
${{\mathcal {E}}}_i|_C$ has infinite monodromy around  $Z_m\cap \bar {C}$, as desired.
$Z_m\cap \bar {C}$, as desired.
Let ![]() $\bar {C}\subset \bar {U}$ be a good curve for the quintuple
$\bar {C}\subset \bar {U}$ be a good curve for the quintuple ![]() $(\bar {X}, X, \bar {U}, \omega _N^{r}, (x_j)^{s}_{j=1})$. Recall the decomposition from (3.1):
$(\bar {X}, X, \bar {U}, \omega _N^{r}, (x_j)^{s}_{j=1})$. Recall the decomposition from (3.1): ![]() $\displaystyle {{\mathcal {E}}}\cong \oplus _{i=1}^{b} {{\mathcal {F}}}_i^{m_i}$, where each
$\displaystyle {{\mathcal {E}}}\cong \oplus _{i=1}^{b} {{\mathcal {F}}}_i^{m_i}$, where each ![]() ${{\mathcal {F}}}_i$ is the sum of the distinct companions of
${{\mathcal {F}}}_i$ is the sum of the distinct companions of ![]() ${{\mathcal {E}}}_i$ under the reordering specified in Step 1. (Note that
${{\mathcal {E}}}_i$ under the reordering specified in Step 1. (Note that ![]() ${{\mathcal {F}}}_i$ has Frobenius traces in
${{\mathcal {F}}}_i$ has Frobenius traces in ![]() ${{\mathbb {Q}}}$.) By Theorem 2.1 and Remark 2.8, for each
${{\mathbb {Q}}}$.) By Theorem 2.1 and Remark 2.8, for each ![]() $i\in \{1,\dots,b\}$, there exists an abelian scheme
$i\in \{1,\dots,b\}$, there exists an abelian scheme ![]() $A_i\rightarrow C$ of dimension
$A_i\rightarrow C$ of dimension ![]() $g_i=[E_i:{{\mathbb {Q}}}]$ such that
$g_i=[E_i:{{\mathbb {Q}}}]$ such that ![]() ${{\mathcal {F}}}_i|_C$ is compatible with
${{\mathcal {F}}}_i|_C$ is compatible with ![]() $A_i$. By taking the iterated fiber product over
$A_i$. By taking the iterated fiber product over ![]() $C$, it therefore follows from (3.2) that there exists an abelian scheme
$C$, it therefore follows from (3.2) that there exists an abelian scheme ![]() $\pi _C\colon A_C\rightarrow C$ of relative dimension
$\pi _C\colon A_C\rightarrow C$ of relative dimension ![]() $g$ such that
$g$ such that
As ![]() $l$ is prime to
$l$ is prime to ![]() $p$, it follows from the Galois correspondence for
$p$, it follows from the Galois correspondence for ![]() $\pi _1(X)$ that the category of (necessarily étale)
$\pi _1(X)$ that the category of (necessarily étale) ![]() $l$-divisible groups on
$l$-divisible groups on ![]() $X$ is equivalent to the category of lisse
$X$ is equivalent to the category of lisse ![]() $\mathbb {Z}_l$ sheaves on
$\mathbb {Z}_l$ sheaves on ![]() $X$ (see, for example, [Reference Chai, Conrad and OortCCO14, pp. 147–148], where they explain that the functor is explicitly given as the Tate
$X$ (see, for example, [Reference Chai, Conrad and OortCCO14, pp. 147–148], where they explain that the functor is explicitly given as the Tate ![]() $l$-group). Write
$l$-group). Write ![]() $\Phi$ for an inverse functor. We have assumed that the
$\Phi$ for an inverse functor. We have assumed that the ![]() ${{\mathbb {Z}}}_l$-lattice
${{\mathbb {Z}}}_l$-lattice ![]() $\tilde {L}$ has trivial residual representation, that is, the following map is trivial:
$\tilde {L}$ has trivial residual representation, that is, the following map is trivial:
Then it follows from the Galois correspondence that ![]() $\Phi (\tilde {L})[l]$ is isomorphic to the split étale group scheme
$\Phi (\tilde {L})[l]$ is isomorphic to the split étale group scheme ![]() $({{\mathbb {Z}}}/l{{\mathbb {Z}}})^{2g}$ (see, for example, the explicit formula on [Reference Chai, Conrad and OortCCO14, p. 148]). On the other hand,
$({{\mathbb {Z}}}/l{{\mathbb {Z}}})^{2g}$ (see, for example, the explicit formula on [Reference Chai, Conrad and OortCCO14, p. 148]). On the other hand, ![]() $\Phi (\tilde {L})$ is isogenous to
$\Phi (\tilde {L})$ is isogenous to ![]() $A_C[l^{\infty }]$ because
$A_C[l^{\infty }]$ because ![]() $\tilde {L}$ is isogenous to
$\tilde {L}$ is isogenous to ![]() $T_l(A_C)$. It follows from Lemma 2.13 that there exists an
$T_l(A_C)$. It follows from Lemma 2.13 that there exists an ![]() $l$-primary isogeny
$l$-primary isogeny ![]() $A_C\rightarrow A'_C$ over
$A_C\rightarrow A'_C$ over ![]() $C$ such that
$C$ such that ![]() $A'_C[l]\rightarrow C$ is isomorphic to the split étale group scheme
$A'_C[l]\rightarrow C$ is isomorphic to the split étale group scheme ![]() $({{\mathbb {Z}}}/l{{\mathbb {Z}}})^{2g}$. The abelian scheme
$({{\mathbb {Z}}}/l{{\mathbb {Z}}})^{2g}$. The abelian scheme ![]() $A'_C\rightarrow C$ therefore has a full collection of
$A'_C\rightarrow C$ therefore has a full collection of ![]() $l$-torsion sections, that is, it has trivial
$l$-torsion sections, that is, it has trivial ![]() $l$-torsion. Replacing
$l$-torsion. Replacing ![]() $A_C$ by
$A_C$ by ![]() $A_C'$, we may assume that
$A_C'$, we may assume that ![]() $A_C$ has trivial
$A_C$ has trivial ![]() $l$-torsion.
$l$-torsion.
Similarly, we claim that ![]() $\mathbb {D}(A_C[p^{\infty }])\otimes \overline {\mathbb {Q}}_p\cong {{\mathcal {E}}}|_C$. Indeed,
$\mathbb {D}(A_C[p^{\infty }])\otimes \overline {\mathbb {Q}}_p\cong {{\mathcal {E}}}|_C$. Indeed, ![]() $\mathbb {D}(A_C[p^{\infty }])\otimes \overline {\mathbb {Q}}_p$ is a semi-simple object of
$\mathbb {D}(A_C[p^{\infty }])\otimes \overline {\mathbb {Q}}_p$ is a semi-simple object of ![]() $\textbf {F-Isoc}^{{\dagger} }({C})_{\overline {\mathbb {Q}}_p}$ by [Reference PálPál15] and is compatible with
$\textbf {F-Isoc}^{{\dagger} }({C})_{\overline {\mathbb {Q}}_p}$ by [Reference PálPál15] and is compatible with ![]() $L|_C$ by [Reference Katz and MessingKM74]. Therefore,
$L|_C$ by [Reference Katz and MessingKM74]. Therefore, ![]() $\mathbb {D}(A_C[p^{\infty }])$ is isogenous to
$\mathbb {D}(A_C[p^{\infty }])$ is isogenous to ![]() $(M,F,V)_C$ as Dieudonné crystals on
$(M,F,V)_C$ as Dieudonné crystals on ![]() $C$. We claim that we may replace
$C$. We claim that we may replace ![]() $A_C$ by an (
$A_C$ by an (![]() $p$-primarily) isogenous abelian scheme in order to ensure that
$p$-primarily) isogenous abelian scheme in order to ensure that
as Dieudonné crystals on ![]() $C$. To see this, use [Reference de JongdJ95] to construct a
$C$. To see this, use [Reference de JongdJ95] to construct a ![]() $p$-divisible group
$p$-divisible group ![]() $G_C$ on
$G_C$ on ![]() $C$ where
$C$ where ![]() $\mathbb {D}(G_C)\cong (M_C,F,V)$. It follows that
$\mathbb {D}(G_C)\cong (M_C,F,V)$. It follows that ![]() $A_C[p^{\infty }]$ and
$A_C[p^{\infty }]$ and ![]() $G_C$ are isogenous. Applying Lemma 2.13, we see that there is a
$G_C$ are isogenous. Applying Lemma 2.13, we see that there is a ![]() $p$-primary isogeny
$p$-primary isogeny ![]() $A_C\rightarrow A'_C$ such that
$A_C\rightarrow A'_C$ such that ![]() $A'_C[p^{\infty }]\cong G_C$. As the group of
$A'_C[p^{\infty }]\cong G_C$. As the group of ![]() $l$-torsion points of an abelian scheme is a finite flat
$l$-torsion points of an abelian scheme is a finite flat ![]() $l$-primary group scheme, it follows that
$l$-primary group scheme, it follows that ![]() $A'_C$ also has trivial
$A'_C$ also has trivial ![]() $l$-torsion. Replace
$l$-torsion. Replace ![]() $A_C$ by
$A_C$ by ![]() $A'_C$. We emphasize that this choice of
$A'_C$. We emphasize that this choice of ![]() $A_C$ is not canonical!
$A_C$ is not canonical!
By construction, the ![]() $l$-torsion of
$l$-torsion of ![]() $A_C\rightarrow C$ is trivial; it follows that
$A_C\rightarrow C$ is trivial; it follows that ![]() $A_C\rightarrow C$ has semi-stable reduction along
$A_C\rightarrow C$ has semi-stable reduction along ![]() $\bar {C}\cap Z$. (Use that the monodromy representation
$\bar {C}\cap Z$. (Use that the monodromy representation ![]() $\pi _1(C)\rightarrow \mathrm {GL}_{2g}(\mathbb {Z}_l)$ has image in
$\pi _1(C)\rightarrow \mathrm {GL}_{2g}(\mathbb {Z}_l)$ has image in ![]() $\Gamma (l):=\{1+M\,|\ M\in lM_{n\times n}(\mathbb {Z}_l)\}\subset \mathrm {GL}_{2g}(\mathbb {Z}_l)$, and the fact that if
$\Gamma (l):=\{1+M\,|\ M\in lM_{n\times n}(\mathbb {Z}_l)\}\subset \mathrm {GL}_{2g}(\mathbb {Z}_l)$, and the fact that if ![]() $l>2$, the group
$l>2$, the group ![]() $(1+l\overline {\mathbb {Z}}_l)^{\times }$ is torsion-free. Therefore, if
$(1+l\overline {\mathbb {Z}}_l)^{\times }$ is torsion-free. Therefore, if ![]() $\gamma \in \pi _1(C)$ has quasi-unipotent image in the representation, it then in fact has unipotent image. The claim then follows from Grothendieck's semi-stable reduction theorem for abelian varieties.)
$\gamma \in \pi _1(C)$ has quasi-unipotent image in the representation, it then in fact has unipotent image. The claim then follows from Grothendieck's semi-stable reduction theorem for abelian varieties.)
Let ![]() $A_{\bar {C}}\rightarrow \bar {C}$ be the Néron model and let
$A_{\bar {C}}\rightarrow \bar {C}$ be the Néron model and let ![]() $A^{o}_{\bar {C}}\rightarrow \bar {C}$ denote the associated semi-abelian scheme, that is, the open subset of
$A^{o}_{\bar {C}}\rightarrow \bar {C}$ denote the associated semi-abelian scheme, that is, the open subset of ![]() $A_{\bar {C}}\rightarrow C$ obtained by removing the non-identity components along
$A_{\bar {C}}\rightarrow C$ obtained by removing the non-identity components along ![]() $\bar {C}{\setminus} C$. It follows from the third part of Proposition A.11 that the logarithmic Dieudonné crystal of
$\bar {C}{\setminus} C$. It follows from the third part of Proposition A.11 that the logarithmic Dieudonné crystal of ![]() $A_{\bar {C}}\rightarrow \bar {C}$ constructed in Remark A.9 is isomorphic to
$A_{\bar {C}}\rightarrow \bar {C}$ constructed in Remark A.9 is isomorphic to ![]() $(M,F,V)_{\bar {C}}$. Then, by the second part of Proposition A.11, the Hodge bundle of the
$(M,F,V)_{\bar {C}}$. Then, by the second part of Proposition A.11, the Hodge bundle of the ![]() $A^{o}_{\bar {C}}\rightarrow \bar {C}$ is isomorphic to
$A^{o}_{\bar {C}}\rightarrow \bar {C}$ is isomorphic to ![]() $\omega _M|_{\bar {C}}$.
$\omega _M|_{\bar {C}}$.
Set ![]() $B_C:=(A_C\times _C A^{t}_C)^{4}$. By Zarhin's trick [Reference Moret-BaillyMB85, Chapitre IX, Lemme 1.1, p. 205],
$B_C:=(A_C\times _C A^{t}_C)^{4}$. By Zarhin's trick [Reference Moret-BaillyMB85, Chapitre IX, Lemme 1.1, p. 205], ![]() $B_C$ admits a principal polarization. By construction, we have that
$B_C$ admits a principal polarization. By construction, we have that
•
 $B_C$ has trivial
$B_C$ has trivial  $l$-torsion, and
$l$-torsion, and•
 $\mathbb {D}(B_C[p^{\infty }])\cong (N_C,F,V)$.
$\mathbb {D}(B_C[p^{\infty }])\cong (N_C,F,V)$.
By the uniqueness part of Proposition A.11 it follows that there is an isomorphism of logarithmic Dieudonné crystals:
Hence, the Hodge line bundle of ![]() $B^{o}_{\bar {C}}\rightarrow \bar {C}$ is isomorphic to
$B^{o}_{\bar {C}}\rightarrow \bar {C}$ is isomorphic to ![]() $\omega _N|_{\bar {C}}$ again by Proposition A.11. However, we emphasize again that the choice
$\omega _N|_{\bar {C}}$ again by Proposition A.11. However, we emphasize again that the choice ![]() $B_C\rightarrow C$ is not canonical!
$B_C\rightarrow C$ is not canonical!
We have an induced morphism to a fine moduli scheme ![]() $C\rightarrow \mathscr {A}_{8g,1,l}$. This extends to a morphism from
$C\rightarrow \mathscr {A}_{8g,1,l}$. This extends to a morphism from ![]() $\bar{C}$ to the minimal compactification
$\bar{C}$ to the minimal compactification ![]() $\mathscr {A}_{8g,1,l}^{*}/\mathbb {F}_q$ because the latter is proper and the former is a smooth curve:
$\mathscr {A}_{8g,1,l}^{*}/\mathbb {F}_q$ because the latter is proper and the former is a smooth curve:

We now claim the pullback of ![]() $\alpha$, the Hodge line bundle on
$\alpha$, the Hodge line bundle on ![]() $\mathscr {A}^{*}_{8g,1,l}$, is isomorphic to
$\mathscr {A}^{*}_{8g,1,l}$, is isomorphic to ![]() $\omega _N|_{\bar {C}}$. Here is the reason. Choose a toroidal compactification
$\omega _N|_{\bar {C}}$. Here is the reason. Choose a toroidal compactification ![]() $\bar {\mathscr {A}}_{8g,1,l}$. We then have a commutative diagram
$\bar {\mathscr {A}}_{8g,1,l}$. We then have a commutative diagram

again, because ![]() $\bar {\mathscr {A}}_{8g,1,l}/\mathbb {F}_q$ is proper and
$\bar {\mathscr {A}}_{8g,1,l}/\mathbb {F}_q$ is proper and ![]() $\bar {C}/\mathbb {F}_q$ is a smooth curve. By [Reference Faltings and ChaiFC90, Ch. V, Theorem 2.5], there is a semi-abelian scheme
$\bar {C}/\mathbb {F}_q$ is a smooth curve. By [Reference Faltings and ChaiFC90, Ch. V, Theorem 2.5], there is a semi-abelian scheme ![]() $G\rightarrow \bar {\mathscr {A}}_{8g,1,l}$ such that
$G\rightarrow \bar {\mathscr {A}}_{8g,1,l}$ such that ![]() $\varphi ^{*}\alpha$ is isomorphic to the Hodge line bundle of
$\varphi ^{*}\alpha$ is isomorphic to the Hodge line bundle of ![]() $G\rightarrow \bar {\mathscr {A}}_{8g,1,l}$. Now, [Reference Faltings and ChaiFC90, Ch. I, Proposition 2.7] implies that
$G\rightarrow \bar {\mathscr {A}}_{8g,1,l}$. Now, [Reference Faltings and ChaiFC90, Ch. I, Proposition 2.7] implies that ![]() $h^{*}G$ is isomorphic to
$h^{*}G$ is isomorphic to ![]() $A^{o}_{\bar {C}}\rightarrow \bar {C}$, that is, the semi-abelian scheme given by the open subset of
$A^{o}_{\bar {C}}\rightarrow \bar {C}$, that is, the semi-abelian scheme given by the open subset of ![]() $A_{\bar {C}}\rightarrow \bar {C}$ obtained by removing the non-identity components along
$A_{\bar {C}}\rightarrow \bar {C}$ obtained by removing the non-identity components along ![]() $\bar {C}\backslash C$. In particular, it follows from part (2) of Proposition A.11 that the Hodge line bundle of
$\bar {C}\backslash C$. In particular, it follows from part (2) of Proposition A.11 that the Hodge line bundle of ![]() $h^{*}G$ is compatible with the Hodge line bundle constructed in Remark A.8.
$h^{*}G$ is compatible with the Hodge line bundle constructed in Remark A.8.
In (3.3), we have already fixed a basis of sections
after pulling back the sections to ![]() $\bar {C}$ via (3.4), we obtain an
$\bar {C}$ via (3.4), we obtain an ![]() $m+1$-tuple of sections
$m+1$-tuple of sections ![]() $t_0,\dots,t_m$ in
$t_0,\dots,t_m$ in ![]() $H^{0}(\bar {C},\omega ^{r}_N|_{\bar {C}})$ that define the morphism
$H^{0}(\bar {C},\omega ^{r}_N|_{\bar {C}})$ that define the morphism ![]() $\bar {C}\rightarrow \mathscr {A}^{*}_{8g,1,l}\subset \mathbb {P}^{m}$.
$\bar {C}\rightarrow \mathscr {A}^{*}_{8g,1,l}\subset \mathbb {P}^{m}$.
In conclusion, for every good curve ![]() $\bar {C}\subset \bar {U}$ for the quintuple
$\bar {C}\subset \bar {U}$ for the quintuple ![]() $(\bar {X}, X, \bar {U}, \omega _N^{r},(x_j)^{s}_{j=1})$, we have constructed an
$(\bar {X}, X, \bar {U}, \omega _N^{r},(x_j)^{s}_{j=1})$, we have constructed an ![]() $m+1$-tuple of globally generating sections
$m+1$-tuple of globally generating sections ![]() $t_0,\dots,t_m\in H^{0}(\bar {C},\omega ^{r}_N|_{\bar {C}})$ such that
$t_0,\dots,t_m\in H^{0}(\bar {C},\omega ^{r}_N|_{\bar {C}})$ such that
• the induced map lands in
 $\mathscr {A}^{*}_{8g,1,l}\subset \mathbb {P}^{m}$;
$\mathscr {A}^{*}_{8g,1,l}\subset \mathbb {P}^{m}$;• the image of
 $C$ under the induced map lands in
$C$ under the induced map lands in  $\mathscr {A}_{8g,1,l}\subset \mathscr {A}_{8g,1,l}^{*}$;
$\mathscr {A}_{8g,1,l}\subset \mathscr {A}_{8g,1,l}^{*}$;• and such that the induced abelian variety on
 $B_C\rightarrow C$ is isomorphic to
$B_C\rightarrow C$ is isomorphic to  $(A_C\times _C A_C^{t})^{4}$ where
$(A_C\times _C A_C^{t})^{4}$ where  $A_C\rightarrow C$ is an abelian scheme with
$A_C\rightarrow C$ is an abelian scheme with  $\mathbb {D}(A_C[p^{\infty }])\cong (M,F,V)|_C$ as Dieudonné crystals on
$\mathbb {D}(A_C[p^{\infty }])\cong (M,F,V)|_C$ as Dieudonné crystals on  $C$. (Therefore we also have that
$C$. (Therefore we also have that  $\mathbb {D}(B_C[p^{\infty }])\cong (N,F,V)|_C$.)
$\mathbb {D}(B_C[p^{\infty }])\cong (N,F,V)|_C$.)
In particular, setting ![]() $M=\mathscr {A}_{8g,1,l}^{*}\subset \mathbb {P}^{m}$, condition (3) of Lemma 2.9 holds for
$M=\mathscr {A}_{8g,1,l}^{*}\subset \mathbb {P}^{m}$, condition (3) of Lemma 2.9 holds for ![]() $\bar {C}\subset \bar {X}$ (corresponding to the symbols
$\bar {C}\subset \bar {X}$ (corresponding to the symbols ![]() $C\subset Y$ in Lemma 2.9). Note that for two such good curves
$C\subset Y$ in Lemma 2.9). Note that for two such good curves ![]() $C$ and
$C$ and ![]() $C'$, there is no reason that the induced maps to
$C'$, there is no reason that the induced maps to ![]() $\mathscr {A}_{8g,1,l}$ match up on the intersection
$\mathscr {A}_{8g,1,l}$ match up on the intersection ![]() $C\cap C'$ because our choices of abelian schemes were not canonical.
$C\cap C'$ because our choices of abelian schemes were not canonical.
For each ![]() $n>0$, let
$n>0$, let ![]() $P_n$ denote the union of the set of closed points of
$P_n$ denote the union of the set of closed points of ![]() $U$ whose residue field is contained in
$U$ whose residue field is contained in ![]() $\mathbb {F}_{q^{n!}}$. Note that, for any infinite subset
$\mathbb {F}_{q^{n!}}$. Note that, for any infinite subset ![]() $S\subset \mathbb {N}$, the set
$S\subset \mathbb {N}$, the set ![]() $\bigcup _{n\in S}P_n$ is Zariski dense in
$\bigcup _{n\in S}P_n$ is Zariski dense in ![]() $X$; indeed, any given closed point
$X$; indeed, any given closed point ![]() $x$ of
$x$ of ![]() $U$ is an element of
$U$ is an element of ![]() $P_n$ for all
$P_n$ for all ![]() $n\gg 0$. By Lemma 2.12, it follows that, for each
$n\gg 0$. By Lemma 2.12, it follows that, for each ![]() $n>0$, there exists a good curve
$n>0$, there exists a good curve ![]() $\bar {C}_n\subset \bar {U}$ for the quintuple
$\bar {C}_n\subset \bar {U}$ for the quintuple ![]() $(\bar {X}, X, \bar {U}, \omega _N^{r}, P_n)$.
$(\bar {X}, X, \bar {U}, \omega _N^{r}, P_n)$.
For each ![]() $n\in \mathbb {N}$, by the above remarks we obtain an
$n\in \mathbb {N}$, by the above remarks we obtain an ![]() $m+1$-tuple of globally generating sections
$m+1$-tuple of globally generating sections
such that the induced map factors ![]() $f_n\colon \bar {C}_n\rightarrow \mathscr {A}^{*}_{8g,1,l}\subset \mathbb {P}^{m}$. Moreover, any infinite subcollection of the
$f_n\colon \bar {C}_n\rightarrow \mathscr {A}^{*}_{8g,1,l}\subset \mathbb {P}^{m}$. Moreover, any infinite subcollection of the ![]() $\bar {C}_n$ is Zariski dense because they are space-filling: if
$\bar {C}_n$ is Zariski dense because they are space-filling: if ![]() $x$ is a closed point of
$x$ is a closed point of ![]() $U$ with residue field
$U$ with residue field ![]() $\mathbb {F}_{q^{e}}$, then
$\mathbb {F}_{q^{e}}$, then ![]() $x$ is contained in
$x$ is contained in ![]() $C_n$ for all
$C_n$ for all ![]() $n\geq e$. By Lemma 2.9, it follows that there exist an infinite set
$n\geq e$. By Lemma 2.9, it follows that there exist an infinite set ![]() $S\subset \mathbb {N}$ and sections
$S\subset \mathbb {N}$ and sections ![]() $\tilde {t}_0,\dots,\tilde {t}_m\in H^{0}(\bar {X},\omega ^{r}_N)$ such that the induced rational map
$\tilde {t}_0,\dots,\tilde {t}_m\in H^{0}(\bar {X},\omega ^{r}_N)$ such that the induced rational map ![]() $\tilde {f}\colon \bar {X}\dashrightarrow \mathbb {P}^{m}$ lands in
$\tilde {f}\colon \bar {X}\dashrightarrow \mathbb {P}^{m}$ lands in ![]() $\mathscr {A}^{*}_{8g,1,l}$ and, moreover, for each
$\mathscr {A}^{*}_{8g,1,l}$ and, moreover, for each ![]() $n\in S$, we have an equality of morphisms
$n\in S$, we have an equality of morphisms ![]() $\tilde {f}|_{\bar {C}_n}=f_n$.
$\tilde {f}|_{\bar {C}_n}=f_n$.
By shrinking ![]() $U$, we therefore obtain a map
$U$, we therefore obtain a map ![]() $\tilde {f}\colon U\rightarrow \mathscr {A}_{8g,1,l}$ and hence an abelian scheme
$\tilde {f}\colon U\rightarrow \mathscr {A}_{8g,1,l}$ and hence an abelian scheme ![]() ${B_U\rightarrow U}$ such that
${B_U\rightarrow U}$ such that ![]() $B_U[l]$ is a trivial étale cover of
$B_U[l]$ is a trivial étale cover of ![]() $U$. The maps
$U$. The maps ![]() $f_n\colon \bar {C}_n\rightarrow \mathscr {A}_{8g,1,l}^{*}$ were all constructed such that the induced abelian scheme
$f_n\colon \bar {C}_n\rightarrow \mathscr {A}_{8g,1,l}^{*}$ were all constructed such that the induced abelian scheme ![]() $B_{C_n}\rightarrow C_n$ is compatible with
$B_{C_n}\rightarrow C_n$ is compatible with
On the other hand, if ![]() $u$ is a closed point of
$u$ is a closed point of ![]() $U$, then
$U$, then ![]() $u$ lies on
$u$ lies on ![]() $C_n$ for all
$C_n$ for all ![]() $n\gg 0$. We claim that it follows that
$n\gg 0$. We claim that it follows that ![]() $B_U\rightarrow U$ is compatible with
$B_U\rightarrow U$ is compatible with ![]() $(L\oplus L^{*}(-1))^{4}|_U$. Indeed, it suffices to show that for every closed point
$(L\oplus L^{*}(-1))^{4}|_U$. Indeed, it suffices to show that for every closed point ![]() $u$ of
$u$ of ![]() $U$,
$U$, ![]() $B_u\rightarrow u$ and
$B_u\rightarrow u$ and ![]() $(L\oplus L^{*}(-1))^{4}|_u$ are compatible, that is, that the characteristic polynomials of Frobenius match up. Pick
$(L\oplus L^{*}(-1))^{4}|_u$ are compatible, that is, that the characteristic polynomials of Frobenius match up. Pick ![]() $n\in S$ with
$n\in S$ with ![]() $C_n$ containing
$C_n$ containing ![]() $u$. As the map
$u$. As the map ![]() $\tilde {f}\colon U\rightarrow \mathscr {A}_{8g,1,l}$ extends the map
$\tilde {f}\colon U\rightarrow \mathscr {A}_{8g,1,l}$ extends the map ![]() $f_n\colon C_n\rightarrow \mathscr {A}_{8g,1,l}$ by the definition of
$f_n\colon C_n\rightarrow \mathscr {A}_{8g,1,l}$ by the definition of ![]() $S$ in Lemma 2.9, the induced abelian scheme
$S$ in Lemma 2.9, the induced abelian scheme ![]() $B_U\rightarrow U$ extends the abelian scheme
$B_U\rightarrow U$ extends the abelian scheme ![]() $B_{C_n}\rightarrow C_n$ constructed above, which is compatible with
$B_{C_n}\rightarrow C_n$ constructed above, which is compatible with ![]() $(L\oplus L^{*}(-1))^{4}|_{C_n}$ by construction. Therefore
$(L\oplus L^{*}(-1))^{4}|_{C_n}$ by construction. Therefore ![]() $B_u\rightarrow u$ is compatible with
$B_u\rightarrow u$ is compatible with ![]() $(L\oplus L^{*}(-1))^{4}|_{u}$, as desired.
$(L\oplus L^{*}(-1))^{4}|_{u}$, as desired.
For each ![]() $n\in S$ we have that
$n\in S$ we have that ![]() $\tilde {f}|_{\bar {C}_n}=f_n$. By construction there exists an abelian scheme
$\tilde {f}|_{\bar {C}_n}=f_n$. By construction there exists an abelian scheme ![]() $A_{C_n}\rightarrow C_n$ of dimension
$A_{C_n}\rightarrow C_n$ of dimension ![]() $g$ with
$g$ with
Consider the map of representations induced by the first ![]() ${{\mathbb {Z}}}_l$-cohomology of the abelian schemes
${{\mathbb {Z}}}_l$-cohomology of the abelian schemes ![]() $B_U\rightarrow U$ and
$B_U\rightarrow U$ and ![]() $B_U|_{C_n}\rightarrow C_n$:
$B_U|_{C_n}\rightarrow C_n$:

Then [Reference KatzKatz01, Lemma 6(b)] implies that for ![]() $n\gg 0$, the two representations have the same image (which lands in
$n\gg 0$, the two representations have the same image (which lands in ![]() $\mathrm {GL}_{2g}({{\mathbb {Z}}}_l)^{8}$). By the fundamental work of Tate and Zarhin on Tate's isogeny theorem for abelian varieties over finitely generated fields of positive characteristic [Reference Moret-BaillyMB85, Ch. XII, Théorème 2.5(i), p. 244], it follows that, for all
$\mathrm {GL}_{2g}({{\mathbb {Z}}}_l)^{8}$). By the fundamental work of Tate and Zarhin on Tate's isogeny theorem for abelian varieties over finitely generated fields of positive characteristic [Reference Moret-BaillyMB85, Ch. XII, Théorème 2.5(i), p. 244], it follows that, for all ![]() $n\gg 0$, the natural injective map
$n\gg 0$, the natural injective map ![]() $\text {End}_U(B_U)\hookrightarrow \text {End}_{C_n}({B_U|_{C_n}})$ is an isomorphism when tensored with
$\text {End}_U(B_U)\hookrightarrow \text {End}_{C_n}({B_U|_{C_n}})$ is an isomorphism when tensored with ![]() ${{\mathbb {Z}}}_l$ and hence also when tensored with
${{\mathbb {Z}}}_l$ and hence also when tensored with ![]() ${{\mathbb {Q}}}_l$. Therefore, for all
${{\mathbb {Q}}}_l$. Therefore, for all ![]() $n\gg 0$, the map
$n\gg 0$, the map
is an isomorphism as both sides are finite-dimensional semi-simple ![]() ${{\mathbb {Q}}}$-algebras of the same rank.
${{\mathbb {Q}}}$-algebras of the same rank.
We know that ![]() $\text {End}_{C_n}(B_{U}|_{C_n})$ has a non-trivial idempotent
$\text {End}_{C_n}(B_{U}|_{C_n})$ has a non-trivial idempotent ![]() $e_{C_n}$ that projects onto a copy of
$e_{C_n}$ that projects onto a copy of ![]() $A_{C_n}$. After replacing
$A_{C_n}$. After replacing ![]() $e_{C_n}$ by a high integer multiple, we may lift
$e_{C_n}$ by a high integer multiple, we may lift ![]() $e_{C_n}$ to
$e_{C_n}$ to ![]() $e_U\in \text {End}_U(B_U)$. Set the image of
$e_U\in \text {End}_U(B_U)$. Set the image of ![]() $e_U$ to be the abelian scheme
$e_U$ to be the abelian scheme ![]() $\pi _U\colon A_U\rightarrow U$. Finally, we claim that
$\pi _U\colon A_U\rightarrow U$. Finally, we claim that ![]() $A_U$ is compatible with
$A_U$ is compatible with ![]() $L$ (equivalently,
$L$ (equivalently, ![]() ${{\mathcal {E}}}$). Indeed, the image
${{\mathcal {E}}}$). Indeed, the image ![]() $A_U\rightarrow U$ is an abelian scheme of dimension
$A_U\rightarrow U$ is an abelian scheme of dimension ![]() $g$ that extends
$g$ that extends ![]() $A_{C_n}\rightarrow C_n$. On the other hand, in (3.6) the two images in
$A_{C_n}\rightarrow C_n$. On the other hand, in (3.6) the two images in ![]() $\mathrm {GL}_{16g}(\mathbb {Z}_l)$ are the same (as we have assumed
$\mathrm {GL}_{16g}(\mathbb {Z}_l)$ are the same (as we have assumed ![]() $n\gg 0$) and hence have corresponding decompositions in irreducible
$n\gg 0$) and hence have corresponding decompositions in irreducible ![]() $\mathbb {Q}_l$ representations.
$\mathbb {Q}_l$ representations.
Step 3: the proof in the general case via reduction to Step 2. There exists a projective divisorial compactification ![]() $\bar {X}$ of
$\bar {X}$ of ![]() $X$. (This means that
$X$. (This means that ![]() $\bar {X}$ is normal and the boundary is an effective Cartier divisor.) By Kedlaya's semi-stable reduction theorem (see [Reference KedlayaKed22, Theorem 7.6] for a meta-reference), there is a generically étale alteration
$\bar {X}$ is normal and the boundary is an effective Cartier divisor.) By Kedlaya's semi-stable reduction theorem (see [Reference KedlayaKed22, Theorem 7.6] for a meta-reference), there is a generically étale alteration ![]() $\varphi \colon X'\rightarrow X$ together with a simple normal crossings compactification
$\varphi \colon X'\rightarrow X$ together with a simple normal crossings compactification ![]() $\overline {X'}$ such that the overconvergent pullback
$\overline {X'}$ such that the overconvergent pullback ![]() ${{\mathcal {E}}}'$ extends to a logarithmic
${{\mathcal {E}}}'$ extends to a logarithmic ![]() $F$-isocrystal with nilpotent residues. After replacing
$F$-isocrystal with nilpotent residues. After replacing ![]() $X'$ with a further finite étale cover, we may guarantee that the residual representation of
$X'$ with a further finite étale cover, we may guarantee that the residual representation of ![]() $L'$ is trivial.
$L'$ is trivial.
We have proven the theorem for ![]() ${{\mathcal {E}}}'$ on
${{\mathcal {E}}}'$ on ![]() $X'$: there exist an open subset
$X'$: there exist an open subset ![]() $W'\subset X'$ and an abelian scheme
$W'\subset X'$ and an abelian scheme ![]() $A_{W'}\rightarrow W'$ of relative dimension
$A_{W'}\rightarrow W'$ of relative dimension ![]() $g$ with
$g$ with ![]() $\mathbb {D}(A_{W'}[p^{\infty }])\cong {{\mathcal {E}}}'|_{W'}$. After shrinking
$\mathbb {D}(A_{W'}[p^{\infty }])\cong {{\mathcal {E}}}'|_{W'}$. After shrinking ![]() $W'$ and
$W'$ and ![]() $W$, we may assume that
$W$, we may assume that ![]() $\varphi |_{W'}\colon W'\rightarrow W$ is finite étale, of degree
$\varphi |_{W'}\colon W'\rightarrow W$ is finite étale, of degree ![]() $d$.
$d$.
Set ![]() $B_W:=\mathfrak {Res}^{W'}_{W}(A_{W'})$ to be the Weil restriction of scalars. This is an abelian scheme over
$B_W:=\mathfrak {Res}^{W'}_{W}(A_{W'})$ to be the Weil restriction of scalars. This is an abelian scheme over ![]() $W$ of dimension
$W$ of dimension ![]() $dg$. We claim that
$dg$. We claim that ![]() $B_W$ is compatible with
$B_W$ is compatible with ![]() $L^{d}$. One way to see this is as follows. Consider the short exact sequence of abelian sheaves in the étale topology:
$L^{d}$. One way to see this is as follows. Consider the short exact sequence of abelian sheaves in the étale topology:
As ![]() $W'\rightarrow W$ is finite étale, Weil restriction is exact on the level of abelian étale sheaves. Therefore
$W'\rightarrow W$ is finite étale, Weil restriction is exact on the level of abelian étale sheaves. Therefore ![]() $\mathfrak {Res}^{W'}_W(A_{W'}[l^{n}])\cong B_W[l^{n}]$. As
$\mathfrak {Res}^{W'}_W(A_{W'}[l^{n}])\cong B_W[l^{n}]$. As ![]() $A_{W'}[l^{n}]$ is a finite étale group over
$A_{W'}[l^{n}]$ is a finite étale group over ![]() $W$, one deduces that the representation associated to
$W$, one deduces that the representation associated to ![]() $B_W$ is isomorphic to
$B_W$ is isomorphic to
However, ![]() $L'$, as a representation, is the restriction of
$L'$, as a representation, is the restriction of ![]() $L$ along the inclusion
$L$ along the inclusion ![]() $\pi _1(W')\hookrightarrow \pi _1(W)$. Then the desired compatibility follows from the following fact: if
$\pi _1(W')\hookrightarrow \pi _1(W)$. Then the desired compatibility follows from the following fact: if ![]() $H\subset G$ is the inclusion of a subgroup of finite index
$H\subset G$ is the inclusion of a subgroup of finite index ![]() $d$, and if
$d$, and if ![]() $V$ is a finite-dimensional representation of
$V$ is a finite-dimensional representation of ![]() $G$, then
$G$, then
Recall that we wrote an isotypic decomposition:
 \[ \displaystyle L\cong \bigoplus_{i=1}^{a} (L_i)^{m_i} \]
\[ \displaystyle L\cong \bigoplus_{i=1}^{a} (L_i)^{m_i} \]
where each ![]() $L_i$ is irreducible on
$L_i$ is irreducible on ![]() $X$ (and hence on
$X$ (and hence on ![]() $W$ by [Reference KedlayaKed18, Lemma 1.1.2]). Let
$W$ by [Reference KedlayaKed18, Lemma 1.1.2]). Let ![]() $E_i\subset \overline {\mathbb {Q}}_l$ denote the field generated by the traces of Frobenius on
$E_i\subset \overline {\mathbb {Q}}_l$ denote the field generated by the traces of Frobenius on ![]() $L_i$ as
$L_i$ as ![]() $x$ ranges through the closed points of
$x$ ranges through the closed points of ![]() $W$. We claim that we may find a smooth curve
$W$. We claim that we may find a smooth curve ![]() $C\subset W$ with the following properties:
$C\subset W$ with the following properties:
(1) each
 $L_i|_C$ is irreducible;
$L_i|_C$ is irreducible;(2) the field generated by Frobenius traces of
 $L_i|_C$ is
$L_i|_C$ is  $E_i\subset \overline {\mathbb {Q}}_l$;
$E_i\subset \overline {\mathbb {Q}}_l$;(3) each
 $L_i|_{C}$ has infinite monodromy around
$L_i|_{C}$ has infinite monodromy around  $\infty$; and
$\infty$; and(4) the induced monodromy representations coming from
 $B_W\rightarrow W$ and
$B_W\rightarrow W$ and  $B_W|_C\rightarrow C$
have the same image.
$B_W|_C\rightarrow C$
have the same image.
We have a projective normal compactification ![]() $\bar {X}$ of
$\bar {X}$ of ![]() $X$, which is smooth away from a closed subset of codimension at least
$X$, which is smooth away from a closed subset of codimension at least ![]() $2$. Let
$2$. Let ![]() $F=\bar {X}\backslash X$ and let
$F=\bar {X}\backslash X$ and let ![]() $F'\subset F$ be the singular locus of
$F'\subset F$ be the singular locus of ![]() $\bar {X}$. For each
$\bar {X}$. For each ![]() $L_i$, there is an irreducible component
$L_i$, there is an irreducible component ![]() $F_j$ of
$F_j$ of ![]() $F$ that witnesses the fact that
$F$ that witnesses the fact that ![]() $L_i$ has infinite monodromy at
$L_i$ has infinite monodromy at ![]() $\infty$: having infinite monodromy at
$\infty$: having infinite monodromy at ![]() $\infty$ means that a certain inertia group has infinite image in the representation.
$\infty$ means that a certain inertia group has infinite image in the representation.
Pick a closed point ![]() $y_j\in F_j\backslash (F_j\cap F')$ for each
$y_j\in F_j\backslash (F_j\cap F')$ for each ![]() $j$. Then, by using [Reference DrinfeldDri12, C.2], we may construct an infinite set of curves
$j$. Then, by using [Reference DrinfeldDri12, C.2], we may construct an infinite set of curves ![]() $(C_n)_{n\in {{\mathbb {N}}}}$ where each
$(C_n)_{n\in {{\mathbb {N}}}}$ where each ![]() $C_n\subset W$ is a smooth, geometrically connected curve that contains all closed points of
$C_n\subset W$ is a smooth, geometrically connected curve that contains all closed points of ![]() $W$ whose residue fields are contained in
$W$ whose residue fields are contained in ![]() $\mathbb {F}_{q^{n!}}$ and that pass through the
$\mathbb {F}_{q^{n!}}$ and that pass through the ![]() $y_j$ transversally (i.e., with a tangent direction that is not contained in
$y_j$ transversally (i.e., with a tangent direction that is not contained in ![]() $F_j$). (We remark that this is a consequence of Poonen's Bertini theorem [Reference PoonenPoo04, Theorem 1.3].)
$F_j$). (We remark that this is a consequence of Poonen's Bertini theorem [Reference PoonenPoo04, Theorem 1.3].)
Each ![]() $L_i|_{C_n}$ has infinite monodromy around
$L_i|_{C_n}$ has infinite monodromy around ![]() $\infty$. By [Reference KatzKatz01, Lemma 6(b)], it follows that for all
$\infty$. By [Reference KatzKatz01, Lemma 6(b)], it follows that for all ![]() $n\gg 0$,
$n\gg 0$, ![]() $C_n$ satisfies (4). For
$C_n$ satisfies (4). For ![]() $n\gg 0$, [Reference KatzKatz01, Lemma 6(b)] and [Reference DeligneDel12] guarantee that setting
$n\gg 0$, [Reference KatzKatz01, Lemma 6(b)] and [Reference DeligneDel12] guarantee that setting ![]() $C:=C'_n$ satisfies the above four conditions.
$C:=C'_n$ satisfies the above four conditions.
Again, by using Drinfeld's Theorem 2.1, Remark 2.8, and (3.1) as in Step 2, there exists an abelian scheme ![]() $A_{C}\rightarrow C$ that is compatible with
$A_{C}\rightarrow C$ that is compatible with ![]() $L|_{C}$. On the one hand, using the Tate isogeny theorem [Reference Moret-BaillyMB85, Ch. XII, Théorème 2.5], it follows that
$L|_{C}$. On the one hand, using the Tate isogeny theorem [Reference Moret-BaillyMB85, Ch. XII, Théorème 2.5], it follows that ![]() $A^{d}_C$ is isogenous to
$A^{d}_C$ is isogenous to ![]() $B_W|_C$. On the other hand, another application the Tate isogeny theorem together with property (4) of
$B_W|_C$. On the other hand, another application the Tate isogeny theorem together with property (4) of ![]() $C$ implies that the natural map
$C$ implies that the natural map
is an isomorphism after tensoring with ![]() ${{\mathbb {Q}}}$. As
${{\mathbb {Q}}}$. As ![]() $B_W|_C$ is isogenous to
$B_W|_C$ is isogenous to ![]() $A_C^{d}$, it follows that
$A_C^{d}$, it follows that ![]() $\text {End}_{C}(B_W|_C)\otimes {{\mathbb {Q}}}$ has an element
$\text {End}_{C}(B_W|_C)\otimes {{\mathbb {Q}}}$ has an element ![]() $e_{C}$ projecting onto a factor of
$e_{C}$ projecting onto a factor of ![]() $A_C$. After replacing
$A_C$. After replacing ![]() $e_C$ with a high integer multiple, we may lift to
$e_C$ with a high integer multiple, we may lift to ![]() $e_W\in \text {End}_W(B_W)$. Set the image of
$e_W\in \text {End}_W(B_W)$. Set the image of ![]() $e_W$ to be the abelian scheme
$e_W$ to be the abelian scheme ![]() $A_W\rightarrow W$; this is compatible with
$A_W\rightarrow W$; this is compatible with ![]() $L|_W$, as desired.
$L|_W$, as desired.
Proof of Corollary 1.3 Suppose there exists ![]() $\pi _U\colon A_U\rightarrow U$ such that
$\pi _U\colon A_U\rightarrow U$ such that ![]() $R^{1}(\pi _U)_*\overline {\mathbb {Q}}_l$ has
$R^{1}(\pi _U)_*\overline {\mathbb {Q}}_l$ has ![]() $L_1$ as a summand. By the assumption that
$L_1$ as a summand. By the assumption that ![]() $X$ is smooth and geometrically connected, it is irreducible; hence
$X$ is smooth and geometrically connected, it is irreducible; hence ![]() $U\subset X$ is dense. A theorem of Zarhin implies that
$U\subset X$ is dense. A theorem of Zarhin implies that ![]() $R^{1}(\pi _U)_*\mathbb {Q}_l$ is semi-simple [Reference Moret-BaillyMB85, Chapitre XII, Theorem 2.5, pp. 244–245]. The field generated by the characteristic polynomials of
$R^{1}(\pi _U)_*\mathbb {Q}_l$ is semi-simple [Reference Moret-BaillyMB85, Chapitre XII, Theorem 2.5, pp. 244–245]. The field generated by the characteristic polynomials of ![]() $R^{1}(\pi _U)_*\mathbb {Q}_l$ is clearly
$R^{1}(\pi _U)_*\mathbb {Q}_l$ is clearly ![]() ${{\mathbb {Q}}}$; indeed, this follows Weil's theorem that the characteristic polynomial of Frobenius acting on the Tate module of an abelian variety over a finite field has coefficients in
${{\mathbb {Q}}}$; indeed, this follows Weil's theorem that the characteristic polynomial of Frobenius acting on the Tate module of an abelian variety over a finite field has coefficients in ![]() $\mathbb {Z}$ [Reference WeilWei48, IX,X].
$\mathbb {Z}$ [Reference WeilWei48, IX,X].
We claim that ![]() $\mathbb {D}(A_U[p^{\infty }])\otimes \mathbb {Q}_p$ is a semi-simple object of
$\mathbb {D}(A_U[p^{\infty }])\otimes \mathbb {Q}_p$ is a semi-simple object of ![]() $\textbf {F-Isoc}^{{\dagger} }({U})$. This is essentially contained in [Reference PálPál15, Remark 4.11], but some comments are in order.
$\textbf {F-Isoc}^{{\dagger} }({U})$. This is essentially contained in [Reference PálPál15, Remark 4.11], but some comments are in order.
While the statement of [Reference PálPál15, Remark 4.11] assumes that ![]() $U$ is a smooth curve, this assumption is unnecessary. Indeed, the only point where this assumption is used is in the citation of [Reference Kato and TrihanKT03, 4.3–4.8], to argue that the associated
$U$ is a smooth curve, this assumption is unnecessary. Indeed, the only point where this assumption is used is in the citation of [Reference Kato and TrihanKT03, 4.3–4.8], to argue that the associated ![]() $F$-isocrystal is overconvergent. However, [Reference ÉtesseÉte02, Théorème 7] essentially states and proves exactly this: if
$F$-isocrystal is overconvergent. However, [Reference ÉtesseÉte02, Théorème 7] essentially states and proves exactly this: if ![]() $S/k$ is a smooth separated scheme over a field
$S/k$ is a smooth separated scheme over a field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p$ and
$p$ and ![]() $A\rightarrow S$ is an abelian scheme, then
$A\rightarrow S$ is an abelian scheme, then ![]() $R^{1}f_{\text {rig}}(\mathcal {O}_{X/K})$ is an overconvergent
$R^{1}f_{\text {rig}}(\mathcal {O}_{X/K})$ is an overconvergent ![]() $F$-isocrystal on
$F$-isocrystal on ![]() $S$. When
$S$. When ![]() $k$ is perfect, this
$k$ is perfect, this ![]() $F$-isocrystal is isomorphic to
$F$-isocrystal is isomorphic to ![]() $R^{1}f_{\text {crys}}(\mathcal {O}_{X/W})\otimes \mathbb {Q}$ because
$R^{1}f_{\text {crys}}(\mathcal {O}_{X/W})\otimes \mathbb {Q}$ because ![]() $A\rightarrow S$ is smooth and proper (see, for example, [Reference BerthelotBer97, Proposition 1.9]). On the other hand,
$A\rightarrow S$ is smooth and proper (see, for example, [Reference BerthelotBer97, Proposition 1.9]). On the other hand, ![]() $R^{1}f_{\text {crys}}(\mathcal {O}_{X/W})\cong \mathbb {D}(A[p^{\infty }])$. In particular, to obtain the semi-simplicity, one simply combines Corollary 4.9 and Proposition 3.5 of [Reference PálPál15] with the fact that
$R^{1}f_{\text {crys}}(\mathcal {O}_{X/W})\cong \mathbb {D}(A[p^{\infty }])$. In particular, to obtain the semi-simplicity, one simply combines Corollary 4.9 and Proposition 3.5 of [Reference PálPál15] with the fact that ![]() $\mathbb {D}(A_U[p^{\infty }])\in \textbf {F-Isoc}^{{\dagger} }({U})$, exactly as explained in [Reference PálPál15, Remark 4.11].
$\mathbb {D}(A_U[p^{\infty }])\in \textbf {F-Isoc}^{{\dagger} }({U})$, exactly as explained in [Reference PálPál15, Remark 4.11].
As ![]() $\mathbb {D}(A_U[p^{\infty }])\otimes \mathbb {Q}_p$ is isomorphic to the rational crystalline cohomology of
$\mathbb {D}(A_U[p^{\infty }])\otimes \mathbb {Q}_p$ is isomorphic to the rational crystalline cohomology of ![]() $A_U\rightarrow U$, it follows from [Reference Katz and MessingKM74] that
$A_U\rightarrow U$, it follows from [Reference Katz and MessingKM74] that ![]() $\mathbb {D}(A_U[p^{\infty }])\otimes \mathbb {Q}_p$ and
$\mathbb {D}(A_U[p^{\infty }])\otimes \mathbb {Q}_p$ and ![]() $R^{1}(\pi _U)_*\mathbb {Q}_l$ are companions. It follows from Lemma 2.5 that all crystalline companions of
$R^{1}(\pi _U)_*\mathbb {Q}_l$ are companions. It follows from Lemma 2.5 that all crystalline companions of ![]() $L_1|_U$ exist and, moreover, are summands of
$L_1|_U$ exist and, moreover, are summands of ![]() $\mathbb {D}(A_U[p^{\infty }])\otimes \overline {\mathbb {Q}}_p$. Then, by [Reference KedlayaKed18, Corollary 3.3.3], all crystalline companions to
$\mathbb {D}(A_U[p^{\infty }])\otimes \overline {\mathbb {Q}}_p$. Then, by [Reference KedlayaKed18, Corollary 3.3.3], all crystalline companions to ![]() $L_1$ exist.
$L_1$ exist.
Conversely, suppose all crystalline companions ![]() $({{\mathcal {E}}}_i)^{b}_{i=1}$ to
$({{\mathcal {E}}}_i)^{b}_{i=1}$ to ![]() $L_1$ exist. We first of all claim that each
$L_1$ exist. We first of all claim that each ![]() ${{\mathcal {E}}}_i$ has infinite monodromy at
${{\mathcal {E}}}_i$ has infinite monodromy at ![]() $\infty$. Indeed, suppose for contradiction that there existed an alteration
$\infty$. Indeed, suppose for contradiction that there existed an alteration ![]() $f\colon X'\rightarrow X$ and a compactification
$f\colon X'\rightarrow X$ and a compactification ![]() $\overline {X'}$ such that
$\overline {X'}$ such that ![]() $f^{*}{{\mathcal {E}}}_i$ extends to an object
$f^{*}{{\mathcal {E}}}_i$ extends to an object ![]() ${{\mathcal {F}}}'$ of
${{\mathcal {F}}}'$ of ![]() $\textbf {F-Isoc}^{{\dagger} }({\overline {X'}})_{\overline {\mathbb {Q}}_p}$. Then
$\textbf {F-Isoc}^{{\dagger} }({\overline {X'}})_{\overline {\mathbb {Q}}_p}$. Then ![]() $f^{*}L_1$ would also extend to
$f^{*}L_1$ would also extend to ![]() $\overline {X'}$ by [Reference KedlayaKed18, Corollary 3.3.3], contradicting the assumption that
$\overline {X'}$ by [Reference KedlayaKed18, Corollary 3.3.3], contradicting the assumption that ![]() $L_1$ had infinite monodromy at
$L_1$ had infinite monodromy at ![]() $\infty$. Moreover, each
$\infty$. Moreover, each ![]() ${{\mathcal {E}}}_i$ is irreducible by [Reference KedlayaKed18, Lemma 3.3.1]. Similarly, tensorial operations respect the companion relation, hence
${{\mathcal {E}}}_i$ is irreducible by [Reference KedlayaKed18, Lemma 3.3.1]. Similarly, tensorial operations respect the companion relation, hence ![]() $\det ({{\mathcal {E}}}_i)\cong \overline {\mathbb {Q}}_p(-1)$. There exists a
$\det ({{\mathcal {E}}}_i)\cong \overline {\mathbb {Q}}_p(-1)$. There exists a ![]() $p$-adic local field
$p$-adic local field ![]() $K$ with each
$K$ with each ![]() ${{\mathcal {E}}}_i$ an object of
${{\mathcal {E}}}_i$ an object of ![]() $\textbf {F-Isoc}^{{\dagger} }({X})_{K}$. Set
$\textbf {F-Isoc}^{{\dagger} }({X})_{K}$. Set ![]() ${{\mathcal {E}}}:=\bigoplus _{i=1}^{b} {{\mathcal {E}}}_i$, considered as an object of
${{\mathcal {E}}}:=\bigoplus _{i=1}^{b} {{\mathcal {E}}}_i$, considered as an object of ![]() $\textbf {F-Isoc}^{{\dagger} }({X})$ (by restricting scalars from
$\textbf {F-Isoc}^{{\dagger} }({X})$ (by restricting scalars from ![]() $K$ to
$K$ to ![]() $\mathbb {Q}_p$, so the rank of
$\mathbb {Q}_p$, so the rank of ![]() ${{\mathcal {E}}}$ is
${{\mathcal {E}}}$ is ![]() $2b[K:{{\mathbb {Q}}}]$). Note that
$2b[K:{{\mathbb {Q}}}]$). Note that ![]() ${{\mathcal {E}}}$, being the sum of irreducible objects, is semi-simple. Then
${{\mathcal {E}}}$, being the sum of irreducible objects, is semi-simple. Then ![]() ${{\mathcal {E}}}$ satisfies the hypotheses of Theorem 1.2, and
${{\mathcal {E}}}$ satisfies the hypotheses of Theorem 1.2, and ![]() $L_1$ is a companion of a summand of
$L_1$ is a companion of a summand of ![]() ${{\mathcal {E}}}$. It follows that there is an open set
${{\mathcal {E}}}$. It follows that there is an open set ![]() $U\subset X$ together with an abelian scheme
$U\subset X$ together with an abelian scheme ![]() $\pi _U\colon A_U\rightarrow U$ such that
$\pi _U\colon A_U\rightarrow U$ such that ![]() ${{\mathcal {E}}}\cong \mathbb {D}(A_U[p^{\infty })\otimes \mathbb {Q}_p$. Again using Zarhin's semi-simplicity,
${{\mathcal {E}}}\cong \mathbb {D}(A_U[p^{\infty })\otimes \mathbb {Q}_p$. Again using Zarhin's semi-simplicity, ![]() $L_1|_U$ is a summand of
$L_1|_U$ is a summand of ![]() $R^{1}(\pi _U)_*\overline {\mathbb {Q}}_l$, as desired.
$R^{1}(\pi _U)_*\overline {\mathbb {Q}}_l$, as desired.
Proof of Corollary 1.4 Under the assumption on ![]() $E_1$, all
$E_1$, all ![]() $p$-adic companions to
$p$-adic companions to ![]() ${{\mathcal {E}}}_1$ exist by [Reference Krishnamoorthy and PálKP21, Corollary 4.16]. (This result is straightforward; they are all Galois twists of each other.) Fix
${{\mathcal {E}}}_1$ exist by [Reference Krishnamoorthy and PálKP21, Corollary 4.16]. (This result is straightforward; they are all Galois twists of each other.) Fix ![]() $\sigma \colon \overline {\mathbb {Q}}_p \rightarrow \overline {\mathbb {Q}}_l$. Then the
$\sigma \colon \overline {\mathbb {Q}}_p \rightarrow \overline {\mathbb {Q}}_l$. Then the ![]() $\sigma$-companion to
$\sigma$-companion to ![]() ${{\mathcal {E}}}_1$ exists by [Reference Abe and EsnaultAE19, Theorem 4.2] or [Reference KedlayaKed18, Corollary 3.5.3]. Apply Corollary 1.3.
${{\mathcal {E}}}_1$ exists by [Reference Abe and EsnaultAE19, Theorem 4.2] or [Reference KedlayaKed18, Corollary 3.5.3]. Apply Corollary 1.3.
Appendix A. Logarithmic  $F$-crystals
$F$-crystals
We first recall the notion of a logarithmic ![]() $F$-crystal/isocrystal. While this notion is due to Kato [Reference KatoKato89, § 6], our treatment is copied from recent work of Kedlaya.
$F$-crystal/isocrystal. While this notion is due to Kato [Reference KatoKato89, § 6], our treatment is copied from recent work of Kedlaya.
Definition A.1 A smooth pair over a perfect field ![]() $k$ is a pair
$k$ is a pair ![]() $(Y,Z)$ where
$(Y,Z)$ where ![]() $Y/k$ is a smooth variety and
$Y/k$ is a smooth variety and ![]() $Z\subset Y$ is a strict normal crossings divisor.
$Z\subset Y$ is a strict normal crossings divisor.
Definition A.2 Let ![]() $(Y,Z)$ be a smooth pair over a perfect field
$(Y,Z)$ be a smooth pair over a perfect field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$. A smooth chart for
$p>0$. A smooth chart for ![]() $(Y,Z)$ is a sequence of elements
$(Y,Z)$ is a sequence of elements ![]() $\bar {t}_1,\dots,\bar {t}_n$ of elements of
$\bar {t}_1,\dots,\bar {t}_n$ of elements of ![]() ${{\mathcal {O}}}_Y(Y)$ such that
${{\mathcal {O}}}_Y(Y)$ such that
• the induced map
 $\bar {f}\colon Y\rightarrow \mathbb {A}^{n}$ is étale, and
$\bar {f}\colon Y\rightarrow \mathbb {A}^{n}$ is étale, and• there exists an
 $m\in [1,n]$ such that the zero-loci of
$m\in [1,n]$ such that the zero-loci of  $\overline {t_i}$, for
$\overline {t_i}$, for  $i=1,\dots, m$, are exactly the irreducible components of
$i=1,\dots, m$, are exactly the irreducible components of  $Z$.
$Z$.
Smooth charts exist Zariski locally on smooth pairs (in characteristic ![]() $p$) by [Reference KedlayaKed05, Theorem 2]. Let
$p$) by [Reference KedlayaKed05, Theorem 2]. Let ![]() $(Y,Z)$ be a smooth pair over a perfect field
$(Y,Z)$ be a smooth pair over a perfect field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$. Let
$p>0$. Let ![]() $\bar {t}_1,\dots,\bar {t}_n$ be a smooth chart of
$\bar {t}_1,\dots,\bar {t}_n$ be a smooth chart of ![]() $(Y,Z)$. Let
$(Y,Z)$. Let ![]() $P_0$ be the formal scheme given by the formal completion of
$P_0$ be the formal scheme given by the formal completion of ![]() $W(k)[t_1,\dots,t_n]$ along
$W(k)[t_1,\dots,t_n]$ along ![]() $(p)$. By topological invariance of the étale site, there exist a unique smooth formal scheme
$(p)$. By topological invariance of the étale site, there exist a unique smooth formal scheme ![]() $P$ and an étale morphism
$P$ and an étale morphism ![]() $f\colon P\rightarrow P_0$ lifting
$f\colon P\rightarrow P_0$ lifting ![]() $\bar {f}$. We call the pair
$\bar {f}$. We call the pair ![]() $(P,t_1,\dots,t_n)$ the lifted smooth chart of
$(P,t_1,\dots,t_n)$ the lifted smooth chart of ![]() $(Y,Z)$ associated to the original chart.
$(Y,Z)$ associated to the original chart.
Let ![]() $\sigma _0\colon P_0\rightarrow P_0$ be the Frobenius lift with
$\sigma _0\colon P_0\rightarrow P_0$ be the Frobenius lift with ![]() $\sigma ^{*}(t_i)=t_i^{p}$ for
$\sigma ^{*}(t_i)=t_i^{p}$ for ![]() $i\in [1,\dots,n]$. Then there exists an associated Frobenius lift
$i\in [1,\dots,n]$. Then there exists an associated Frobenius lift ![]() $\sigma \colon P\rightarrow P$.
$\sigma \colon P\rightarrow P$.
Definition A.3 Let ![]() $(Y,Z)$ be a smooth pair over a perfect field
$(Y,Z)$ be a smooth pair over a perfect field ![]() $k$ and let
$k$ and let ![]() $\bar {t}_1,\dots,\bar {t}_n$ be a smooth chart of
$\bar {t}_1,\dots,\bar {t}_n$ be a smooth chart of ![]() $(Y,Z)$. Keep notation as above. A logarithmic crystal with nilpotent residues on
$(Y,Z)$. Keep notation as above. A logarithmic crystal with nilpotent residues on ![]() $(Y,Z)$ is a pair
$(Y,Z)$ is a pair ![]() $(M,\nabla )$ where:
$(M,\nabla )$ where:
•
 $M$ is a
$M$ is a  $p$-torsion free coherent module over
$p$-torsion free coherent module over  $P$; and
$P$; and•
 $\nabla$ is an integrable, topologically quasi-nilpotent connection on
$\nabla$ is an integrable, topologically quasi-nilpotent connection on  $M$ (with respect to
$M$ (with respect to  $W(k)$) with logarithmic poles and nilpotent residues along the zero-loci of
$W(k)$) with logarithmic poles and nilpotent residues along the zero-loci of  $f^{*}(t_i)$ for
$f^{*}(t_i)$ for  $i\in 1,\dots,m$.
$i\in 1,\dots,m$.
A logarithmic ![]() $F$-crystal with nilpotent residues is a triple
$F$-crystal with nilpotent residues is a triple ![]() $(M,\nabla,F)$ where
$(M,\nabla,F)$ where ![]() $(M,\nabla )$ is a logarithmic crystal with nilpotent residues and
$(M,\nabla )$ is a logarithmic crystal with nilpotent residues and ![]() $F$ is an injective, horizontal morphism
$F$ is an injective, horizontal morphism
of coherent ![]() $P$-modules. A logarithmic Dieudonné crystal with nilpotent residues is a quadruple
$P$-modules. A logarithmic Dieudonné crystal with nilpotent residues is a quadruple ![]() $(M,\nabla,F,V)$ where
$(M,\nabla,F,V)$ where ![]() $(M,\nabla,F)$ is a logarithmic
$(M,\nabla,F)$ is a logarithmic ![]() $F$-crystal in finite, locally free modules with nilpotent residues and
$F$-crystal in finite, locally free modules with nilpotent residues and ![]() $V$ is an injective, horizontal map
$V$ is an injective, horizontal map
such that ![]() $FV=VF=p$.
$FV=VF=p$.
Remark A.4 In the definition of a logarithmic ![]() $F$-crystal with nilpotent residues, we do not demand that
$F$-crystal with nilpotent residues, we do not demand that ![]() $M$ is locally free. However, in our definition of a logarithmic Dieudonné crystal, we do demand that the underlying logarithmic crystal is locally free.
$M$ is locally free. However, in our definition of a logarithmic Dieudonné crystal, we do demand that the underlying logarithmic crystal is locally free.
This definition extends to general smooth pairs by Zariski gluing; every smooth pair admits a finite open covering on which the restriction admits a smooth chart. We often drop the connection ![]() $\nabla$ from the notation and write a logarithmic
$\nabla$ from the notation and write a logarithmic ![]() $F$-crystal as
$F$-crystal as ![]() $(M,F)$.
$(M,F)$.
There is a natural category of logarithmic crystals with nilpotent residues on ![]() $(Y,Z)$ (where morphisms are
$(Y,Z)$ (where morphisms are ![]() $P$-linear and horizontal), and the category of logarithmic isocrystals with nilpotent residues is defined to be the induced isogeny category. One similarly defines the category of logarithmic
$P$-linear and horizontal), and the category of logarithmic isocrystals with nilpotent residues is defined to be the induced isogeny category. One similarly defines the category of logarithmic ![]() $F$-isocrystals with nilpotent residues.
$F$-isocrystals with nilpotent residues.
Remark A.5 Part of the definition of a logarithmic ![]() $F$-crystal
$F$-crystal ![]() $(M,\nabla,F)$ in Definition A.3 explicitly assumes that the residues of the underlying crystal
$(M,\nabla,F)$ in Definition A.3 explicitly assumes that the residues of the underlying crystal ![]() $(M,\nabla )$ were nilpotent. This assumption is indeed superfluous; we now explain why.
$(M,\nabla )$ were nilpotent. This assumption is indeed superfluous; we now explain why.
First of all, the associated logarithmic isocrystal ![]() $(M,\nabla )\otimes {{\mathbb {Q}}}$ to
$(M,\nabla )\otimes {{\mathbb {Q}}}$ to ![]() $(M,\nabla,F)$ is a convergent logarithmic isocrystal: indeed, a logarithmic isocrystal is convergent if and only if it is infinitely Frobenius divisible; see [Reference OgusOgu95, Remark 16], the argument of which is just a logarithmic variant of [Reference OgusOgu84, 2.18]. (See [Reference BerthelotBer96, § 2.4] or [Reference Esnault and ShihoES18, Remark 2.4] for several other perspectives in the non-logarithmic setting.) Then it is a general fact that a convergent logarithmic
$(M,\nabla,F)$ is a convergent logarithmic isocrystal: indeed, a logarithmic isocrystal is convergent if and only if it is infinitely Frobenius divisible; see [Reference OgusOgu95, Remark 16], the argument of which is just a logarithmic variant of [Reference OgusOgu84, 2.18]. (See [Reference BerthelotBer96, § 2.4] or [Reference Esnault and ShihoES18, Remark 2.4] for several other perspectives in the non-logarithmic setting.) Then it is a general fact that a convergent logarithmic ![]() $F$-isocrystal has nilpotent residues; see, for example, [Reference KedlayaKed22, Definition 7.2].
$F$-isocrystal has nilpotent residues; see, for example, [Reference KedlayaKed22, Definition 7.2].
Remark A.6 Let ![]() $(Y,Z)$ be a smooth pair over
$(Y,Z)$ be a smooth pair over ![]() $k$ and let
$k$ and let ![]() $U=Y\backslash Z$. We denote by
$U=Y\backslash Z$. We denote by ![]() $\underline {Y}$ the (fine, saturated) logarithmic scheme given by
$\underline {Y}$ the (fine, saturated) logarithmic scheme given by ![]() $(Y,\alpha \colon {{\mathcal {O}}}_U^{*}\hookrightarrow {{\mathcal {O}}}_Y)$. Then our definition of a logarithmic crystal is compatible with the definition of Kato (see [Reference KatoKato89, Theorem 6.2]), our definition of a logarithmic
$(Y,\alpha \colon {{\mathcal {O}}}_U^{*}\hookrightarrow {{\mathcal {O}}}_Y)$. Then our definition of a logarithmic crystal is compatible with the definition of Kato (see [Reference KatoKato89, Theorem 6.2]), our definition of a logarithmic ![]() $F$-crystal in finite, locally free modules is compatible with the definition of Kato and Trihan (see [Reference Kato and TrihanKT03, 4.1]) and our definition of a logarithmic
$F$-crystal in finite, locally free modules is compatible with the definition of Kato and Trihan (see [Reference Kato and TrihanKT03, 4.1]) and our definition of a logarithmic ![]() $F$-isocrystal is compatible with the definition given by Shiho (see [Reference ShihoShi00, Definition 4.1.3]).
$F$-isocrystal is compatible with the definition given by Shiho (see [Reference ShihoShi00, Definition 4.1.3]).
The mathematical content of the following lemma is essentially [Reference KatzKatz79, Theorem 2.6.1] (and relatedly [Reference CrewCre87, Lemma 2.5.1]); we have simply rewritten Katz's argument in the logarithmic setting. The key is that Katz's slope bounds holding on the open subset where the logarithmic structure is trivial guarantees that they hold everywhere. We use Kato's definition of logarithmic ![]() $F$-crystals only for convenience to discuss global objects; all of the computations use the local definitions given above.
$F$-crystals only for convenience to discuss global objects; all of the computations use the local definitions given above.
Lemma A.7 Let ![]() $(Y,Z)$ be a smooth pair over a perfect field
$(Y,Z)$ be a smooth pair over a perfect field ![]() $k$ of positive characteristic and let
$k$ of positive characteristic and let ![]() $U:=Y\backslash Z$. Let
$U:=Y\backslash Z$. Let ![]() ${{\mathcal {E}}}$ be a logarithmic
${{\mathcal {E}}}$ be a logarithmic ![]() $F$-isocrystal on
$F$-isocrystal on ![]() $(Y,Z)$.
$(Y,Z)$.
(1) Suppose the Newton slopes of
 ${{\mathcal {E}}}_U$ are all non-negative. Then there exist an open subset
${{\mathcal {E}}}_U$ are all non-negative. Then there exist an open subset  $W\subset Y$, whose complementary codimension is at least
$W\subset Y$, whose complementary codimension is at least  $2$, and a logarithmic
$2$, and a logarithmic  $F$-crystal in finite, locally free modules
$F$-crystal in finite, locally free modules  $(M'',F)$ on the smooth pair
$(M'',F)$ on the smooth pair  $(W,W\cap Z)$ such that
$(W,W\cap Z)$ such that  ${(M'',F)\otimes {{\mathbb {Q}}}\cong {{\mathcal {E}}}_W}$.
${(M'',F)\otimes {{\mathbb {Q}}}\cong {{\mathcal {E}}}_W}$.(2) Suppose the Newton slopes of
 ${{\mathcal {E}}}_U$ are in the interval
${{\mathcal {E}}}_U$ are in the interval  $[0,1]$. Then there exist an open subset
$[0,1]$. Then there exist an open subset  $W\subset Y$, whose complementary codimension is at least
$W\subset Y$, whose complementary codimension is at least  $2$, and a logarithmic Dieudonné crystal in finite, locally free modules
$2$, and a logarithmic Dieudonné crystal in finite, locally free modules  $(M'',F,V)$ on the smooth pair
$(M'',F,V)$ on the smooth pair  $(W,W\cap Z)$ such that
$(W,W\cap Z)$ such that  $(M'',F)\otimes {{\mathbb {Q}}}\cong {{\mathcal {E}}}_W$.
$(M'',F)\otimes {{\mathbb {Q}}}\cong {{\mathcal {E}}}_W$.
Proof. By the definition of a logarithmic ![]() $F$-isocrystal, there exist a logarithmic crystal in coherent (not necessarily locally free!) modules
$F$-isocrystal, there exist a logarithmic crystal in coherent (not necessarily locally free!) modules ![]() $M$ and a map
$M$ and a map ![]() $F\colon \textit {Frob}_{\underline Y}^{*} M\rightarrow M\otimes {{\mathbb {Q}}}$ that is isomorphic to
$F\colon \textit {Frob}_{\underline Y}^{*} M\rightarrow M\otimes {{\mathbb {Q}}}$ that is isomorphic to ![]() ${{\mathcal {E}}}$ when thought of as a logarithmic
${{\mathcal {E}}}$ when thought of as a logarithmic ![]() $F$-isocrystal. Here,
$F$-isocrystal. Here, ![]() $\textit {Frob}_{\underline Y}$ refers to the absolute Frobenius (on the fine and saturated (f.s.) log scheme
$\textit {Frob}_{\underline Y}$ refers to the absolute Frobenius (on the fine and saturated (f.s.) log scheme ![]() $\underline {Y}$ induced from the smooth pair
$\underline {Y}$ induced from the smooth pair ![]() $(Y,Z)$) and the
$(Y,Z)$) and the ![]() $*$ refers to pullback on the logarithmic crystalline topos. This is compatible with our above definitions.
$*$ refers to pullback on the logarithmic crystalline topos. This is compatible with our above definitions.
As ![]() $M$ is a logarithmic crystal in coherent modules, there exists a non-negative integer
$M$ is a logarithmic crystal in coherent modules, there exists a non-negative integer ![]() $\nu$ so that
$\nu$ so that
We have assumed that the Newton slopes of ![]() ${{\mathcal {E}}}$ are all non-negative. Slope bounds of Katz (see the proof on [Reference KatzKatz79, pp. 151–152]) imply then that there exists a non-negative
${{\mathcal {E}}}$ are all non-negative. Slope bounds of Katz (see the proof on [Reference KatzKatz79, pp. 151–152]) imply then that there exists a non-negative ![]() $\nu$ such that, for all
$\nu$ such that, for all ![]() $n\geq 0$,
$n\geq 0$,
We explicate this in local coordinates. Take an affine open neighborhood ![]() $T\subset Y$ such that
$T\subset Y$ such that ![]() $(T,T\cap Z)$ has a smooth chart
$(T,T\cap Z)$ has a smooth chart ![]() $(\bar {t}_1,\dots,\bar {t}_n)$. Let
$(\bar {t}_1,\dots,\bar {t}_n)$. Let ![]() $(P,t_1,\dots,t_n)$ be the associated lifted smooth chart; note that
$(P,t_1,\dots,t_n)$ be the associated lifted smooth chart; note that ![]() $P=\text {Spf}(A)$ where
$P=\text {Spf}(A)$ where ![]() $A$ is a noetherian
$A$ is a noetherian ![]() $W(k)$ algebra equipped with the
$W(k)$ algebra equipped with the ![]() $p$-adic topology. Then the logarithmic crystal yields a finitely generated
$p$-adic topology. Then the logarithmic crystal yields a finitely generated ![]() $A$ module
$A$ module ![]() $M_A$ and the Frobenius structure induces a continuous,
$M_A$ and the Frobenius structure induces a continuous, ![]() $A$-linear homomorphism
$A$-linear homomorphism ![]() $F\colon \sigma ^{*}M_A\rightarrow p^{-\mu }M_A$.
$F\colon \sigma ^{*}M_A\rightarrow p^{-\mu }M_A$.
As ![]() $U\cap T\subset T$ is open dense, it follows from (A.1) that
$U\cap T\subset T$ is open dense, it follows from (A.1) that
By varying ![]() $T$, one deduces that
$T$, one deduces that ![]() $F^{n}\colon (\textit {Frob}^{n}_{\underline Y})^{*}M\rightarrow p^{-\nu }M$ for our fixed
$F^{n}\colon (\textit {Frob}^{n}_{\underline Y})^{*}M\rightarrow p^{-\nu }M$ for our fixed ![]() $\nu$ as above and for all
$\nu$ as above and for all ![]() $n\geq 0$.
$n\geq 0$.
Consider the module
As ![]() $A$ is noetherian,
$A$ is noetherian, ![]() $M_A'$ is finitely generated, being a submodule of a finitely generated module. Moreover,
$M_A'$ is finitely generated, being a submodule of a finitely generated module. Moreover, ![]() $M_A'$ is stable under
$M_A'$ is stable under ![]() $F$. Finally,
$F$. Finally, ![]() $M_A'$ is the finite sum of (logarithmic) horizontal submodules. Therefore the pair
$M_A'$ is the finite sum of (logarithmic) horizontal submodules. Therefore the pair ![]() $(M_A',F)$ is in fact a logarithmic
$(M_A',F)$ is in fact a logarithmic ![]() $F$-crystal in coherent modules. We have an isomorphism
$F$-crystal in coherent modules. We have an isomorphism ![]() $(M_A',F)\otimes {{\mathbb {Q}}}\cong {{\mathcal {E}}}_T$ in the category of logarithmic
$(M_A',F)\otimes {{\mathbb {Q}}}\cong {{\mathcal {E}}}_T$ in the category of logarithmic ![]() $F$-isocrystals with nilpotent residues on
$F$-isocrystals with nilpotent residues on ![]() $(T,Z\cap T)$.
$(T,Z\cap T)$.
Now set ![]() $M_A'':=(M_A')^{**}$. This is a coherent reflexive sheaf on the ring
$M_A'':=(M_A')^{**}$. This is a coherent reflexive sheaf on the ring ![]() $A$, and hence is locally free away on an open set of
$A$, and hence is locally free away on an open set of ![]() $\operatorname {Spec}(A)$ whose complement has codimension at least 3 [Sta20, 0AY6].
$\operatorname {Spec}(A)$ whose complement has codimension at least 3 [Sta20, 0AY6]. ![]() $M_A''$ is manifestly stable under the connection and
$M_A''$ is manifestly stable under the connection and ![]() $F$. In particular, we can find an open subset
$F$. In particular, we can find an open subset ![]() $T''\subset T$ with complementary codimension at least
$T''\subset T$ with complementary codimension at least ![]() $2$ such that the logarithmic
$2$ such that the logarithmic ![]() $F$-crystal
$F$-crystal ![]() $(M_A'',F)_{T''}$ is a crystal in finite, locally free modules.
$(M_A'',F)_{T''}$ is a crystal in finite, locally free modules.
After initially choosing a pair ![]() $(M,F\colon \textit {Frob}_{\underline {Y}}^{*}M\rightarrow p^{-\mu }M)$ representing
$(M,F\colon \textit {Frob}_{\underline {Y}}^{*}M\rightarrow p^{-\mu }M)$ representing ![]() ${{\mathcal {E}}}$, the constructions we have made are canonical. Therefore, ranging over
${{\mathcal {E}}}$, the constructions we have made are canonical. Therefore, ranging over ![]() $T$, we may glue the
$T$, we may glue the ![]() $(M'',F)_{T''}$; that is, there is an open subset
$(M'',F)_{T''}$; that is, there is an open subset ![]() $W\subset T$ with complementary codimension at least
$W\subset T$ with complementary codimension at least ![]() $2$ and a logarithmic
$2$ and a logarithmic ![]() $F$-crystal
$F$-crystal ![]() $(M'',F)_W$ in finite, locally free modules on the smooth pair
$(M'',F)_W$ in finite, locally free modules on the smooth pair ![]() $(W,Z\cap W)$ that is a lattice inside of
$(W,Z\cap W)$ that is a lattice inside of ![]() ${{\mathcal {E}}}_W$.
${{\mathcal {E}}}_W$.
We now indicate how to complete the result if the Newton polygons on ![]() $U$ are in the interval
$U$ are in the interval ![]() $[0,1]$. Let
$[0,1]$. Let ![]() $(M,F)$ be a logarithmic
$(M,F)$ be a logarithmic ![]() $F$-crystal in finite, locally free modules on a smooth pair
$F$-crystal in finite, locally free modules on a smooth pair ![]() $(Y,Z)$ over a perfect field
$(Y,Z)$ over a perfect field ![]() $k$ and suppose the Newton slopes on
$k$ and suppose the Newton slopes on ![]() $U$ are no greater than 1. Set
$U$ are no greater than 1. Set ![]() $V:=F^{-1}\circ p$. Then
$V:=F^{-1}\circ p$. Then ![]() $V$ does not necessarily stabilize
$V$ does not necessarily stabilize ![]() $M$; however, the pair
$M$; however, the pair ![]() $(M,V)_U$ is a logarithmic
$(M,V)_U$ is a logarithmic ![]() $\sigma ^{-1}$-
$\sigma ^{-1}$-![]() $F$-isocrystal in the language of [Reference KatzKatz79]. (Fortunately, Katz's entire paper is written in the context of
$F$-isocrystal in the language of [Reference KatzKatz79]. (Fortunately, Katz's entire paper is written in the context of ![]() $\sigma ^{a}$-
$\sigma ^{a}$-![]() $F$-crystals for any
$F$-crystals for any ![]() $a\neq 0$, not just the positive
$a\neq 0$, not just the positive ![]() $a$. In particular, all of Katz's results also hold for
$a$. In particular, all of Katz's results also hold for ![]() $\sigma ^{-1}$-
$\sigma ^{-1}$-![]() $F$-crystals. Katz does not deal with logarithmic crystals, but we only use the slope bounds on the open set
$F$-crystals. Katz does not deal with logarithmic crystals, but we only use the slope bounds on the open set ![]() $U$.) By the coherence argument as above, we may find
$U$.) By the coherence argument as above, we may find ![]() $\eta$ such that
$\eta$ such that
on all of ![]() $Y$. Again, using Katz's slope bounds on
$Y$. Again, using Katz's slope bounds on ![]() $U$ (which hold equally well for
$U$ (which hold equally well for ![]() $\sigma ^{-1}$-
$\sigma ^{-1}$-![]() $F$-crystals) and the same coherence argument, one shows that after possibly increasing
$F$-crystals) and the same coherence argument, one shows that after possibly increasing ![]() $\eta$, we in fact have
$\eta$, we in fact have
for all ![]() $n\geq 0$. Now run exactly the above argument with
$n\geq 0$. Now run exactly the above argument with ![]() $V$ instead of
$V$ instead of ![]() $F$: then
$F$: then
will be coherent, horizontal, and stabilized by ![]() $V$. Recall that
$V$. Recall that ![]() $FV=VF=p$; therefore,
$FV=VF=p$; therefore, ![]() $M'$ is also stabilized by
$M'$ is also stabilized by ![]() $F$! Then
$F$! Then ![]() $M'':=(M')^{**}$ is a reflexive logarithmic crystal on
$M'':=(M')^{**}$ is a reflexive logarithmic crystal on ![]() $(Y,Z)$ that is stabilized by both
$(Y,Z)$ that is stabilized by both ![]() $F$ and
$F$ and ![]() $V$. Exactly as above, there exists an open subset
$V$. Exactly as above, there exists an open subset ![]() $W\subset Y$ of complementary codimension at least
$W\subset Y$ of complementary codimension at least ![]() $2$ such that
$2$ such that ![]() $(M'',F,V)_W$ is a logarithmic Dieudonné crystal in finite, locally free modules, as desired.
$(M'',F,V)_W$ is a logarithmic Dieudonné crystal in finite, locally free modules, as desired.
Remark A.8 Let ![]() $(Y,Z)$ be a smooth pair over
$(Y,Z)$ be a smooth pair over ![]() $k$ and let
$k$ and let ![]() $(M,F,V)$ be a logarithmic Dieudonné crystal (in finite, locally free modules) on
$(M,F,V)$ be a logarithmic Dieudonné crystal (in finite, locally free modules) on ![]() $(Y,Z)$. We construct a natural line bundle
$(Y,Z)$. We construct a natural line bundle ![]() $\omega$, which we call the Hodge line bundle, attached to
$\omega$, which we call the Hodge line bundle, attached to ![]() $(M,F,V)$.
$(M,F,V)$.
Evaluating ![]() $M$ on the trivial thickening of
$M$ on the trivial thickening of ![]() $(Y,Z)$, we obtain a vector bundle
$(Y,Z)$, we obtain a vector bundle ![]() $M_{(Y,Z)}$ on
$M_{(Y,Z)}$ on ![]() $Y$ together with an integrable connection with logarithmic poles on
$Y$ together with an integrable connection with logarithmic poles on ![]() $Z$ and a horizontal map:
$Z$ and a horizontal map:
The kernel is a vector bundle on ![]() $Y$. Set
$Y$. Set ![]() $\omega :=\det (\text {ker}(F_{(Y,Z)}))$. We call
$\omega :=\det (\text {ker}(F_{(Y,Z)}))$. We call ![]() $\omega$ the Hodge line bundle associated to
$\omega$ the Hodge line bundle associated to ![]() $(M,F)$.
$(M,F)$.
As a reference for this remark: in the case when ![]() $Z$ is empty, one finds this construction in [Reference de JongdJ98, 2.5.2 and 2.5.5]. In the setting of logarithmic Dieudonné crystals, Kato and Trihan construct the dual object:
$Z$ is empty, one finds this construction in [Reference de JongdJ98, 2.5.2 and 2.5.5]. In the setting of logarithmic Dieudonné crystals, Kato and Trihan construct the dual object: ![]() $Lie(M,F,V)$ (see [Reference Kato and TrihanKT03, 5.1] and especially [Reference Kato and TrihanKT03, Lemma 5.3]. Note that this lemma holds in our situation: our hypothesis that
$Lie(M,F,V)$ (see [Reference Kato and TrihanKT03, 5.1] and especially [Reference Kato and TrihanKT03, Lemma 5.3]. Note that this lemma holds in our situation: our hypothesis that ![]() $(Y,Z)$ is a smooth pair over a perfect field
$(Y,Z)$ is a smooth pair over a perfect field ![]() $k$ implies that the conditions of 5.1 of [Reference Kato and TrihanKT03, p. 563] hold: étale locally, there is a
$k$ implies that the conditions of 5.1 of [Reference Kato and TrihanKT03, p. 563] hold: étale locally, there is a ![]() $p$-basis of
$p$-basis of ![]() $Y$ such that each (regular) component of
$Y$ such that each (regular) component of ![]() $Z$ is cut out by some member of the
$Z$ is cut out by some member of the ![]() $p$-basis.
$p$-basis.
Remark A.9 Let ![]() $Y/k$ be a smooth scheme over a perfect field
$Y/k$ be a smooth scheme over a perfect field ![]() $k$. Let
$k$. Let ![]() $A_Y\rightarrow Y$ be an abelian scheme. Then there is an associated Dieudonné crystal
$A_Y\rightarrow Y$ be an abelian scheme. Then there is an associated Dieudonné crystal ![]() $(M,F,V)=\mathbb {D}(A_Y[p^{\infty }])$ on
$(M,F,V)=\mathbb {D}(A_Y[p^{\infty }])$ on ![]() $Y$ [Reference Berthelot, Breen and MessingBBM82]. The Hodge bundle of
$Y$ [Reference Berthelot, Breen and MessingBBM82]. The Hodge bundle of ![]() $(M,F)$ is isomorphic to the Hodge line bundle of the abelian scheme
$(M,F)$ is isomorphic to the Hodge line bundle of the abelian scheme ![]() $A_Y\rightarrow Y$ by [Reference Berthelot, Breen and MessingBBM82, 3.3.5 and 4.3.10].
$A_Y\rightarrow Y$ by [Reference Berthelot, Breen and MessingBBM82, 3.3.5 and 4.3.10].
Finally, we have the following key Proposition A.11, which furnishes several compatibilities that we need for our main argument. The proof of the proposition largely amounts to collating well-known results in the theory of ![]() $F$-(iso)crystals. We first require the following setup.
$F$-(iso)crystals. We first require the following setup.
Setup A.10 Let ![]() $C/k$ be a smooth, proper, geometrically irreducible curve over a perfect field
$C/k$ be a smooth, proper, geometrically irreducible curve over a perfect field ![]() $k$ of characteristic
$k$ of characteristic ![]() $p>0$, let
$p>0$, let ![]() $U\subset C$ be an open dense subset, and let
$U\subset C$ be an open dense subset, and let ![]() $Z\subset C$ be the reduced complement. Let
$Z\subset C$ be the reduced complement. Let ![]() $A_U\rightarrow U$ be an abelian scheme with semi-stable reduction along
$A_U\rightarrow U$ be an abelian scheme with semi-stable reduction along ![]() $Z$. Call the Néron model
$Z$. Call the Néron model ![]() $A_C\rightarrow C$. Then there is an attached logarithmic Dieudonné crystal on
$A_C\rightarrow C$. Then there is an attached logarithmic Dieudonné crystal on ![]() $(C,Z)$, which we call
$(C,Z)$, which we call ![]() $\mathbb{D}^{\log}(A_C)$ [Reference Kato and TrihanKT03, 4.4–4.8]. (Kato and Trihan construct a covariant Dieudonné functor. We assume ours is contravariant, which may be accomplished by taking a dual as in [Reference Kato and TrihanKT03, 4.1].)
$\mathbb{D}^{\log}(A_C)$ [Reference Kato and TrihanKT03, 4.4–4.8]. (Kato and Trihan construct a covariant Dieudonné functor. We assume ours is contravariant, which may be accomplished by taking a dual as in [Reference Kato and TrihanKT03, 4.1].)
Proposition A.11 In the context of Setup A.10, the following assertions hold.
(1) The (non-logarithmic) Dieudonné crystal
 $\mathbb{D}^{\log}(A_C)|_U$ is isomorphic to the crystalline Dieudonné module of the
$\mathbb{D}^{\log}(A_C)|_U$ is isomorphic to the crystalline Dieudonné module of the  $p$-divisible group
$p$-divisible group  $A_U[p^{\infty }]$
$A_U[p^{\infty }]$(2) Let
 $A^{o}_C\rightarrow C$ be the semi-abelian scheme associated to
$A^{o}_C\rightarrow C$ be the semi-abelian scheme associated to  $A_C\rightarrow C$, obtained by removing the non-identity components of the fibers over
$A_C\rightarrow C$, obtained by removing the non-identity components of the fibers over  $Z$.The Hodge line bundle of
$Z$.The Hodge line bundle of  $A^{o}_C\rightarrow C$, is isomorphic to the Hodge line bundle of the logarithmic Dieudonné crystal
$A^{o}_C\rightarrow C$, is isomorphic to the Hodge line bundle of the logarithmic Dieudonné crystal  $\mathbb{D}^{\log}(A_C)$ described in Remark A.8.
$\mathbb{D}^{\log}(A_C)$ described in Remark A.8.(3) The logarithmic Dieudonné crystal
 $\mathbb{D}^{\log}(A_C)$ is the unique logarithmic Dieudonné crystal (with nilpotent residues) on
$\mathbb{D}^{\log}(A_C)$ is the unique logarithmic Dieudonné crystal (with nilpotent residues) on  $(C,Z)$ that extends
$(C,Z)$ that extends  $\mathbb {D}(A_U[p^{\infty }])$.
$\mathbb {D}(A_U[p^{\infty }])$.
Proof. We prove each point in turn. Point (1) follows by the construction of the logarithmic Dieudonné module: see the description of gluing as in [Reference Kato and TrihanKT03, Lemma 4.4.1].
Point (2) is given in [Reference Kato and TrihanKT03, Example 5.4(b)], with the caveat that they work with the covariant Dieudonné functor and ![]() $\text {Lie}(A_C\rightarrow C)$.
$\text {Lie}(A_C\rightarrow C)$.
We now prove point (3). First of all, note that we only need to check that there is at most one extension as a logarithmic ![]() $F$-crystal in finite, locally free modules. In our setting,
$F$-crystal in finite, locally free modules. In our setting, ![]() $V$ is determined by
$V$ is determined by ![]() $F$ under the relation
$F$ under the relation ![]() $FV=VF=p$. By [Reference ÉtesseÉte02, Théorème 7], it follows that
$FV=VF=p$. By [Reference ÉtesseÉte02, Théorème 7], it follows that ![]() $\mathbb {D}(A_U[p^{\infty }])\otimes \mathbb {Q}_p$ is overconvergent. Forgetting the
$\mathbb {D}(A_U[p^{\infty }])\otimes \mathbb {Q}_p$ is overconvergent. Forgetting the ![]() $V$-structure, we are left with a logarithmic
$V$-structure, we are left with a logarithmic ![]() $F$-crystal
$F$-crystal ![]() $(M,F)$ on
$(M,F)$ on ![]() $(C,Z)$. (By Remark A.5, the residues of
$(C,Z)$. (By Remark A.5, the residues of ![]() $(M,F)$ are automatically nilpotent.) Note that
$(M,F)$ are automatically nilpotent.) Note that ![]() $(M,F)|_U$ is an overconvergent
$(M,F)|_U$ is an overconvergent ![]() $F$-crystal by [Reference KedlayaKed04].
$F$-crystal by [Reference KedlayaKed04].
We are now able to prove the desired uniqueness. Let ![]() $(N,F)$ be a logarithmic
$(N,F)$ be a logarithmic ![]() $F$-crystal on
$F$-crystal on ![]() $(C,Z)$ such that
$(C,Z)$ such that ![]() $(M,F)|_U\cong (N,F)|_U$. (By the above,
$(M,F)|_U\cong (N,F)|_U$. (By the above, ![]() $(N,F)$ automatically has nilpotent residues along
$(N,F)$ automatically has nilpotent residues along ![]() $Z$.) We introduce the following notation.
$Z$.) We introduce the following notation.
•
 $\textbf {FC}({C,Z})$ is the category of logarithmic
$\textbf {FC}({C,Z})$ is the category of logarithmic  $F$-crystals in finite, locally free modules (with nilpotent residues) on
$F$-crystals in finite, locally free modules (with nilpotent residues) on  $(C,Z)$.
$(C,Z)$.•
 $\textbf {FC}({U})$ is the category of
$\textbf {FC}({U})$ is the category of  $F$-crystals in finite, locally free modules on
$F$-crystals in finite, locally free modules on  $U$.
$U$.•
 $\textbf {F-Isoc}({C,Z})$ is the category of logarithmic
$\textbf {F-Isoc}({C,Z})$ is the category of logarithmic  $F$-isocrystals (with nilpotent residues) on
$F$-isocrystals (with nilpotent residues) on  $(C,Z)$.
$(C,Z)$.•
 $\textbf {F-Isoc}({U})$ is the category of (convergent)
$\textbf {F-Isoc}({U})$ is the category of (convergent)  $F$-isocrystals (with nilpotent residues) on
$F$-isocrystals (with nilpotent residues) on  $U$.
$U$.
Consider the following diagram:

To prove that ![]() $(M,F)\cong (N,F)$ in the category
$(M,F)\cong (N,F)$ in the category ![]() $\textbf {FC}({C,Z})$, it suffices to show that the top horizontal arrow is an isomorphism. We first prove that this arrow is injective with torsion cokernel; then we will show that the image is
$\textbf {FC}({C,Z})$, it suffices to show that the top horizontal arrow is an isomorphism. We first prove that this arrow is injective with torsion cokernel; then we will show that the image is ![]() $p$-saturated.
$p$-saturated.
The natural map
is an isomorphism by a full-faithfulness result of Kedlaya [Reference KedlayaKed07, Theorem 6.4.5]. It follows immediately that the bottom horizontal arrow of (A.2) is an isomorphism. (See also [Reference KedlayaKed22, Theorem 7.3] for exactly this statement.)
The group ![]() $\textrm {Hom}_{\textbf {FC}({C,Z})}((M,F),(N,F))$ is a finite free
$\textrm {Hom}_{\textbf {FC}({C,Z})}((M,F),(N,F))$ is a finite free ![]() $\mathbb {Z}_p$-module because
$\mathbb {Z}_p$-module because ![]() $(C,Z)/k$ is log smooth. The left vertical arrow of (A.2) is injective because it is simply the map
$(C,Z)/k$ is log smooth. The left vertical arrow of (A.2) is injective because it is simply the map ![]() $\otimes {{\mathbb {Q}}}$ on a finite free
$\otimes {{\mathbb {Q}}}$ on a finite free ![]() $\mathbb {Z}_p$-module.
$\mathbb {Z}_p$-module.
The group ![]() $\textrm {Hom}_{\textbf {FC}({U})}((M,F)|_U,(N,F)|_U)$ is a priori only a torsion-free
$\textrm {Hom}_{\textbf {FC}({U})}((M,F)|_U,(N,F)|_U)$ is a priori only a torsion-free ![]() $\mathbb {Z}_p$-module. (In particular, it could have infinite rank.) However, the right vertical arrow fits into the following diagram:
$\mathbb {Z}_p$-module. (In particular, it could have infinite rank.) However, the right vertical arrow fits into the following diagram:

where the vertical arrow is an isomorphism by [Reference KedlayaKed04]. As
is a finite-dimensional ![]() $\mathbb {Q}_p$-vector space, it follows that
$\mathbb {Q}_p$-vector space, it follows that ![]() $\textrm {Hom}_{\textbf {FC}({U})}((M,F)|_U,(N,F)|_U)$ is a finite free
$\textrm {Hom}_{\textbf {FC}({U})}((M,F)|_U,(N,F)|_U)$ is a finite free ![]() $\mathbb {Z}_p$-module. As the diagonal arrow is injective (it is the map
$\mathbb {Z}_p$-module. As the diagonal arrow is injective (it is the map ![]() $\otimes {{\mathbb {Q}}}$), we deduce that
$\otimes {{\mathbb {Q}}}$), we deduce that
is also injective. Then the top arrow, ![]() $\text {res}$, in diagram (A.2) must be injective with torsion cokernel by consideration of the ranks.
$\text {res}$, in diagram (A.2) must be injective with torsion cokernel by consideration of the ranks.
Finally, we prove that ![]() $\text {res}$ is a saturated map of finite free
$\text {res}$ is a saturated map of finite free ![]() $\mathbb {Z}_p$ modules. Equivalently, we prove that if
$\mathbb {Z}_p$ modules. Equivalently, we prove that if ![]() $\varphi \in \textrm {Hom}_{\textbf {FC}({C,Z})}((M,F),(N,F))$ is such that
$\varphi \in \textrm {Hom}_{\textbf {FC}({C,Z})}((M,F),(N,F))$ is such that ![]() $\text {res}(\varphi )$ is divisible by
$\text {res}(\varphi )$ is divisible by ![]() $p$ in
$p$ in ![]() $\textrm {Hom}_{\textbf {FC}({U})}((M,F)|_U,(N,F)|_U)$, then
$\textrm {Hom}_{\textbf {FC}({U})}((M,F)|_U,(N,F)|_U)$, then ![]() $\varphi$ is divisible by
$\varphi$ is divisible by ![]() $p$. This will use an explicit local calculation with Definition A.3.
$p$. This will use an explicit local calculation with Definition A.3.
Pick smooth charts for ![]() $(C,Z)$. More precisely,
$(C,Z)$. More precisely, ![]() $C$ may be covered by open subsets
$C$ may be covered by open subsets ![]() $Y_i$ such that there exist étale maps
$Y_i$ such that there exist étale maps ![]() $\bar {f}_i\colon Y_i\rightarrow \mathbb {A}^{1}=\operatorname {Spec}(k[x])$ with the following property: if
$\bar {f}_i\colon Y_i\rightarrow \mathbb {A}^{1}=\operatorname {Spec}(k[x])$ with the following property: if ![]() $Y_i\cap Z\neq \emptyset$, then
$Y_i\cap Z\neq \emptyset$, then ![]() $Y_i\cap Z=\bar {f}_i^{*}(V(x))$. As both the categories of logarithmic
$Y_i\cap Z=\bar {f}_i^{*}(V(x))$. As both the categories of logarithmic ![]() $F$-crystals and usual
$F$-crystals and usual ![]() $F$-crystals are stacks in the Zariski topology, it suffices to prove the desired saturatedness for a single
$F$-crystals are stacks in the Zariski topology, it suffices to prove the desired saturatedness for a single ![]() $(Y_i,Y_i\cap Z)$, which we relabel
$(Y_i,Y_i\cap Z)$, which we relabel ![]() $(Y,Y\cap Z)$. If
$(Y,Y\cap Z)$. If ![]() $Y\cap Z=\emptyset$, there is nothing to prove, so we may assume that
$Y\cap Z=\emptyset$, there is nothing to prove, so we may assume that ![]() $Y\cap Z\neq \emptyset$.
$Y\cap Z\neq \emptyset$.
Let ![]() $\bar {f}\colon Y\rightarrow \mathbb {A}^{1}$ be an étale map with
$\bar {f}\colon Y\rightarrow \mathbb {A}^{1}$ be an étale map with ![]() $\bar {f}^{*}(V(x))=Y\cap Z$, which exists by the definition of
$\bar {f}^{*}(V(x))=Y\cap Z$, which exists by the definition of ![]() $Y$. Let
$Y$. Let ![]() $A_0:=W(k)[x]^{\wedge }$ be the
$A_0:=W(k)[x]^{\wedge }$ be the ![]() $p$-adic completion of
$p$-adic completion of ![]() $W(k)[x]$. By topological invariance of the étale site, the map
$W(k)[x]$. By topological invariance of the étale site, the map ![]() $k[x]\rightarrow \mathcal {O}_Y(Y)$ (with
$k[x]\rightarrow \mathcal {O}_Y(Y)$ (with ![]() $x\mapsto \bar f$) deforms to an étale map
$x\mapsto \bar f$) deforms to an étale map ![]() $A_0\rightarrow A$; set
$A_0\rightarrow A$; set ![]() $f$ to be the image of
$f$ to be the image of ![]() $x$ in
$x$ in ![]() $A$. Similarly, let
$A$. Similarly, let ![]() $B_0=W(k)[x,x^{-1}]^{\wedge }$ be the
$B_0=W(k)[x,x^{-1}]^{\wedge }$ be the ![]() $p$-adic completion of
$p$-adic completion of ![]() $W(k)[x,x^{-1}]$. Again using topological invariance of the étale site, the map
$W(k)[x,x^{-1}]$. Again using topological invariance of the étale site, the map ![]() $k[x,x^{-1}]\rightarrow \mathcal {O}_Y(Y{\setminus} (Y\cap Z))$ induced from
$k[x,x^{-1}]\rightarrow \mathcal {O}_Y(Y{\setminus} (Y\cap Z))$ induced from ![]() $\bar f$ deforms to an étale map
$\bar f$ deforms to an étale map ![]() $B_0\rightarrow B$. As
$B_0\rightarrow B$. As ![]() $Y\cap Z=\bar {f}^{*}(V(x))$, we have that
$Y\cap Z=\bar {f}^{*}(V(x))$, we have that ![]() $B\cong A\hat {\otimes }_{A_0} B_0$. In particular, there is the following diagram of
$B\cong A\hat {\otimes }_{A_0} B_0$. In particular, there is the following diagram of ![]() $p$-adic rings:
$p$-adic rings:

As in Definition A.3, equip ![]() $A_0$ and
$A_0$ and ![]() $B_0$ with the Frobenius lift
$B_0$ with the Frobenius lift ![]() $\sigma _0$ sending
$\sigma _0$ sending ![]() $t\mapsto t^{p}$. Set
$t\mapsto t^{p}$. Set ![]() $\sigma$ to be the induced Frobenius lift on
$\sigma$ to be the induced Frobenius lift on ![]() $A$ and
$A$ and ![]() $B$.
$B$.
Let ![]() $(M,\nabla,F)$ and
$(M,\nabla,F)$ and ![]() $(N,\nabla,F)$ be the realizations of
$(N,\nabla,F)$ be the realizations of ![]() $(M,F)$ and
$(M,F)$ and ![]() $(N,F)$ on
$(N,F)$ on ![]() $A$ as in Definition A.3. In particular,
$A$ as in Definition A.3. In particular, ![]() $M$ and
$M$ and ![]() $N$ are finite, locally free
$N$ are finite, locally free ![]() $A$ modules. Then the statement we wish to prove is that
$A$ modules. Then the statement we wish to prove is that
is a saturated map of ![]() $\mathbb {Z}_p$ modules, that is, if
$\mathbb {Z}_p$ modules, that is, if ![]() $\varphi \in \textrm {Hom}_A((M,\nabla,F),(N,\nabla,F))$ is a map such that
$\varphi \in \textrm {Hom}_A((M,\nabla,F),(N,\nabla,F))$ is a map such that ![]() $\varphi _B$ is divisible by
$\varphi _B$ is divisible by ![]() $p$ in
$p$ in ![]() $\textrm {Hom}_B((M,\nabla,F)_B,(N,\nabla,F)_B)$, then
$\textrm {Hom}_B((M,\nabla,F)_B,(N,\nabla,F)_B)$, then ![]() $\varphi$ was divisible by
$\varphi$ was divisible by ![]() $p$. In particular, we assume that
$p$. In particular, we assume that ![]() $\varphi (M_B)\subset pN_B$ and wish to prove that
$\varphi (M_B)\subset pN_B$ and wish to prove that ![]() $\varphi (M)\subset pN$; indeed, if
$\varphi (M)\subset pN$; indeed, if ![]() $\varphi (M)\subset pN$, then
$\varphi (M)\subset pN$, then ![]() $ {\varphi }/{p}$ will automatically commute with
$ {\varphi }/{p}$ will automatically commute with ![]() $\nabla$ and
$\nabla$ and ![]() $F$ and hence would yield an element
$F$ and hence would yield an element ![]() $ {\varphi }/{p}\in \textrm {Hom}_A((M,\nabla,F),(N,\nabla,F))$. Therefore, it suffices to prove that if
$ {\varphi }/{p}\in \textrm {Hom}_A((M,\nabla,F),(N,\nabla,F))$. Therefore, it suffices to prove that if ![]() $M$ and
$M$ and ![]() $N$ are finite, locally free
$N$ are finite, locally free ![]() $A$ modules, then the map
$A$ modules, then the map ![]() $\textrm {Hom}_A(M,N)\rightarrow \textrm {Hom}_B(M_B,N_B)$ is
$\textrm {Hom}_A(M,N)\rightarrow \textrm {Hom}_B(M_B,N_B)$ is ![]() $p$-saturated.
$p$-saturated.
We claim that ![]() $A\hookrightarrow B$ is a
$A\hookrightarrow B$ is a ![]() $p$-saturated map of
$p$-saturated map of ![]() $p$-adic rings. As noted above,
$p$-adic rings. As noted above, ![]() $B\cong A\hat {\otimes }_{A_0} B_0$; therefore, to prove that
$B\cong A\hat {\otimes }_{A_0} B_0$; therefore, to prove that ![]() $A\hookrightarrow B$ is a
$A\hookrightarrow B$ is a ![]() $p$-saturated, it suffices to prove that
$p$-saturated, it suffices to prove that ![]() $A_0\hookrightarrow B_0$ is
$A_0\hookrightarrow B_0$ is ![]() $p$-saturated. This map is simply the inclusion
$p$-saturated. This map is simply the inclusion ![]() $W(k)[x]^{\wedge }\hookrightarrow W(k)[x,x^{-1}]^{\wedge }$, which is clearly
$W(k)[x]^{\wedge }\hookrightarrow W(k)[x,x^{-1}]^{\wedge }$, which is clearly ![]() $p$-saturated from the explicit description of the elements of the two rings as series.
$p$-saturated from the explicit description of the elements of the two rings as series.
As ![]() $M$ and
$M$ and ![]() $N$ are finite locally free
$N$ are finite locally free ![]() $A$-modules, the natural map
$A$-modules, the natural map ![]() $\textrm {Hom}_A(M,N)\otimes _A B\rightarrow \textrm {Hom}_B(M_B,N_B)$ is an isomorphism. It follows that the natural map
$\textrm {Hom}_A(M,N)\otimes _A B\rightarrow \textrm {Hom}_B(M_B,N_B)$ is an isomorphism. It follows that the natural map
is ![]() $p$-saturated, as desired.
$p$-saturated, as desired.
Acknowledgements
This work was born at CIRM (in Luminy) at ‘![]() $p$-adic Analytic Geometry and Differential Equations’; the authors thank the organizers. R.K. warmly thanks Valery Alexeev, Philip Engel, Kiran Kedlaya, Daniel Litt, and especially Johan de Jong, with whom he had stimulating discussions on the topic of this paper. In addition, the authors heartily thank the anonymous referee for a detailed, thorough, and helpful report. R.K. gratefully acknowledges financial support from the NSF under grants no. DMS-1605825 and no. DMS-1344994 (RTG in Algebra, Algebraic Geometry and Number Theory at the University of Georgia).
$p$-adic Analytic Geometry and Differential Equations’; the authors thank the organizers. R.K. warmly thanks Valery Alexeev, Philip Engel, Kiran Kedlaya, Daniel Litt, and especially Johan de Jong, with whom he had stimulating discussions on the topic of this paper. In addition, the authors heartily thank the anonymous referee for a detailed, thorough, and helpful report. R.K. gratefully acknowledges financial support from the NSF under grants no. DMS-1605825 and no. DMS-1344994 (RTG in Algebra, Algebraic Geometry and Number Theory at the University of Georgia).