Article contents
The Manin constant in the semistable case
Published online by Cambridge University Press: 13 August 2018
Abstract
For an optimal modular parametrization 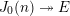 $J_{0}(n){\twoheadrightarrow}E$ of an elliptic curve
$J_{0}(n){\twoheadrightarrow}E$ of an elliptic curve 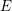 $E$ over
$E$ over 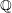 $\mathbb{Q}$ of conductor
$\mathbb{Q}$ of conductor  $n$, Manin conjectured the agreement of two natural
$n$, Manin conjectured the agreement of two natural 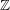 $\mathbb{Z}$-lattices in the
$\mathbb{Z}$-lattices in the 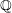 $\mathbb{Q}$-vector space
$\mathbb{Q}$-vector space 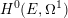 $H^{0}(E,\unicode[STIX]{x1D6FA}^{1})$. Multiple authors generalized his conjecture to higher-dimensional newform quotients. We prove the Manin conjecture for semistable
$H^{0}(E,\unicode[STIX]{x1D6FA}^{1})$. Multiple authors generalized his conjecture to higher-dimensional newform quotients. We prove the Manin conjecture for semistable 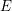 $E$, give counterexamples to all the proposed generalizations, and prove several semistable special cases of these generalizations. The proofs establish general relations between the integral
$E$, give counterexamples to all the proposed generalizations, and prove several semistable special cases of these generalizations. The proofs establish general relations between the integral 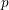 $p$-adic étale and de Rham cohomologies of abelian varieties over
$p$-adic étale and de Rham cohomologies of abelian varieties over 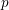 $p$-adic fields and exhibit a new exactness result for Néron models.
$p$-adic fields and exhibit a new exactness result for Néron models.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2018
References
- 6
- Cited by

