Article contents
Le complémentaire des puissances  $n$-ièmes dans un corps de nombres est un ensemble diophantien
$n$-ièmes dans un corps de nombres est un ensemble diophantien
Published online by Cambridge University Press: 22 June 2015
Abstract
For 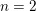 $n=2$ the statement in the title is a theorem of B. Poonen (2009). He uses a one-parameter family of varieties together with a theorem of Coray, Sansuc and one of the authors (1980), on the Brauer–Manin obstruction for rational points on these varieties. For
$n=2$ the statement in the title is a theorem of B. Poonen (2009). He uses a one-parameter family of varieties together with a theorem of Coray, Sansuc and one of the authors (1980), on the Brauer–Manin obstruction for rational points on these varieties. For 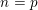 $n=p$,
$n=p$, 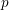 $p$ any prime number, A. Várilly-Alvarado and B. Viray (2012) considered analogous families of varieties. Replacing this family by its
$p$ any prime number, A. Várilly-Alvarado and B. Viray (2012) considered analogous families of varieties. Replacing this family by its 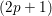 $(2p+1)$th symmetric power, we prove the statement in the title using a theorem on the Brauer–Manin obstruction for rational points on such symmetric powers. The latter theorem is based on work of one of the authors with Swinnerton-Dyer (1994) and with Skorobogatov and Swinnerton-Dyer (1998), work generalising results of Salberger (1988).
$(2p+1)$th symmetric power, we prove the statement in the title using a theorem on the Brauer–Manin obstruction for rational points on such symmetric powers. The latter theorem is based on work of one of the authors with Swinnerton-Dyer (1994) and with Skorobogatov and Swinnerton-Dyer (1998), work generalising results of Salberger (1988).
Samenvatting
Voor 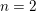 $n=2$ is de bewering in de titel een stelling van B. Poonen (2009). Hij gebruikt een één-parameter familie van variëteiten, en een stelling van Coray, Sansuc en één van de auteurs (1980), over de Brauer–Manin obstructie voor de rationale punten van deze variëteiten. Voor
$n=2$ is de bewering in de titel een stelling van B. Poonen (2009). Hij gebruikt een één-parameter familie van variëteiten, en een stelling van Coray, Sansuc en één van de auteurs (1980), over de Brauer–Manin obstructie voor de rationale punten van deze variëteiten. Voor 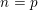 $n=p$,
$n=p$, 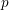 $p$ een willekeurig priemgetal, beschouwden A. Várilly-Alvarado en B. Viray (2012) een analoge familie van variëteiten. We bewijzen de bewering in de titel door deze familie te vervangen door de
$p$ een willekeurig priemgetal, beschouwden A. Várilly-Alvarado en B. Viray (2012) een analoge familie van variëteiten. We bewijzen de bewering in de titel door deze familie te vervangen door de 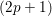 $(2p+1)$-de symmetrische macht ervan en door een stelling over de Brauer–Manin obstructie voor de rationale punten van zulke symmetrische machten toe te passen. Deze stelling steunt op werk van één van de auteurs met Swinnerton-Dyer (1994) en met Skorobogatov en Swinnerton-Dyer (1998). Dat werk veralgemeent resultaten van Salberger (1988).
$(2p+1)$-de symmetrische macht ervan en door een stelling over de Brauer–Manin obstructie voor de rationale punten van zulke symmetrische machten toe te passen. Deze stelling steunt op werk van één van de auteurs met Swinnerton-Dyer (1994) en met Skorobogatov en Swinnerton-Dyer (1998). Dat werk veralgemeent resultaten van Salberger (1988).
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2015
References
- 3
- Cited by

