1. Introduction
In this paper, we study the generalised André–Pink–Zannier conjecture for all Shimura varieties, whose statement is as follows.
Conjecture 1.1 (Generalised André–Pink–Zannier)
Let ![]() $S$ be a Shimura variety and
$S$ be a Shimura variety and ![]() $\Sigma$ a subset of a generalised Hecke orbit in
$\Sigma$ a subset of a generalised Hecke orbit in ![]() $S$. Then the irreducible components of the Zariski closure of
$S$. Then the irreducible components of the Zariski closure of ![]() $\Sigma$ are weakly special subvarieties.
$\Sigma$ are weakly special subvarieties.
We refer to [Reference DeligneDel71, Reference DeligneDel79] for notions and notation concerning Shimura data and Shimura varieties. We refer to [Reference Ullmo and YafaevUY11, Definition 2.1] for definitions and properties of weakly special subvarieties. We refer to Definition 2.1 or § 1.1 for the notion of generalised Hecke orbits.
1.1 Main result
Let ![]() $(G,X)$ be a Shimura datum, let
$(G,X)$ be a Shimura datum, let ![]() $K\leq G({\mathbb {A}}_f)$ be a compact open subgroup, and let
$K\leq G({\mathbb {A}}_f)$ be a compact open subgroup, and let ![]() $S=Sh_K(G,X)=G({\mathbb {Q}})\backslash X\times G({\mathbb {A}}_f)/K$ be the associated Shimura variety. Let
$S=Sh_K(G,X)=G({\mathbb {Q}})\backslash X\times G({\mathbb {A}}_f)/K$ be the associated Shimura variety. Let ![]() $x_0\in X$ and denote by
$x_0\in X$ and denote by ![]() $M\leq G$ its Mumford–Tate group. Let
$M\leq G$ its Mumford–Tate group. Let ![]() $s_0:=[x_0,1]\in S$.
$s_0:=[x_0,1]\in S$.
The generalised Hecke orbit of ![]() $x_0$ in
$x_0$ in ![]() $X$ (see § 2.1) is the set
$X$ (see § 2.1) is the set ![]() $\mathcal {H}(x_0)$ of the
$\mathcal {H}(x_0)$ of the ![]() $\phi \circ x_0$, where
$\phi \circ x_0$, where ![]() $\phi :M\to G$ ranges through the morphisms of
$\phi :M\to G$ ranges through the morphisms of ![]() ${\mathbb {Q}}$-algebraic groups such that
${\mathbb {Q}}$-algebraic groups such that ![]() $\phi \circ x_0\in X$. The generalised Hecke orbit of
$\phi \circ x_0\in X$. The generalised Hecke orbit of ![]() $s_0$ in
$s_0$ in ![]() $S$ is
$S$ is ![]() $\mathcal {H}(s_0):=G({\mathbb {Q}})\backslash \mathcal {H}(x_0)\times G({\mathbb {A}}_f)/K\subseteq S$. For a sufficiently large field
$\mathcal {H}(s_0):=G({\mathbb {Q}})\backslash \mathcal {H}(x_0)\times G({\mathbb {A}}_f)/K\subseteq S$. For a sufficiently large field ![]() $E$ of finite type over
$E$ of finite type over ![]() ${\mathbb {Q}}$ we have the following (see § 3.1):
${\mathbb {Q}}$ we have the following (see § 3.1): ![]() $S$ and
$S$ and ![]() $s_0$ are defined over
$s_0$ are defined over ![]() $E$ and there exists a Galois representation
$E$ and there exists a Galois representation ![]() $\rho _{x_0}:Gal(\overline {E}/E)\to M({\mathbb {A}}_f)\cap K$ such that
$\rho _{x_0}:Gal(\overline {E}/E)\to M({\mathbb {A}}_f)\cap K$ such that
The main result of this paper is the following.
Theorem 1.2 We consider the above situation. We assume the weakly adelic Mumford–Tate hypothesis (see § 6.3), which states that, with ![]() $U:=\rho _{x_0}(Gal(\overline {E}/E))\subseteq M({\mathbb {A}}_f)\cap K$:
$U:=\rho _{x_0}(Gal(\overline {E}/E))\subseteq M({\mathbb {A}}_f)\cap K$:
Then, for any subset ![]() $\Sigma \subseteq \mathcal {H}(s_0)$, every irreducible component of
$\Sigma \subseteq \mathcal {H}(s_0)$, every irreducible component of ![]() $\overline {\Sigma }^{\rm Zar}$ is weakly special.
$\overline {\Sigma }^{\rm Zar}$ is weakly special.
Our ‘weakly adelic Mumford–Tate hypothesis’ is weaker than the adelic form of the Mumford–Tate conjecture [Reference SerreSer94b, 11.4?] stated by Serre. Here are some instances in which above Theorem 1.2 implies Conjecture 1.1 unconditionally.
Combining Theorem 1.2 with Lemma 6.12, one recovers the following.
Theorem 1.3 [Reference Edixhoven and YafaevEY03, Reference Klingler and YafaevKY14]
Conjecture 1.1 is true if ![]() $\Sigma$ contains a special point.
$\Sigma$ contains a special point.
Combining Theorem 1.2 with with [Reference Cadoret and MoonenCM20, Theorem A (i)] we have the following, which strictly contains a 2005 result of Pink [Reference PinkPin05, § 7] (and [Reference Cadoret and KretCK16, Theorem B]).
Theorem 1.4 Conjecture 1.1 is true if ![]() $S$ is of abelian type, and
$S$ is of abelian type, and ![]() $\Sigma$ contains a point
$\Sigma$ contains a point ![]() $s$ which satisfies the Mumford–Tate conjecture (at some
$s$ which satisfies the Mumford–Tate conjecture (at some ![]() $\ell$, in the sense of [Reference Ullmo and YafaevUY13]).
$\ell$, in the sense of [Reference Ullmo and YafaevUY13]).
The assumptions of Theorem 1.4 are satisfied in the case where ![]() $S=\mathcal {A}_g$ and
$S=\mathcal {A}_g$ and ![]() $\Sigma$ contains a point
$\Sigma$ contains a point ![]() $[A]$, where the abelian variety
$[A]$, where the abelian variety ![]() $A$ satisfies the Mumford–Tate conjecture (at some prime
$A$ satisfies the Mumford–Tate conjecture (at some prime ![]() $\ell$). Examples of such abelian varieties are: when
$\ell$). Examples of such abelian varieties are: when ![]() $\dim (A)\leq 3$; or when
$\dim (A)\leq 3$; or when ![]() $\dim (A)$ is odd and
$\dim (A)$ is odd and ![]() ${\rm End}(A)\simeq {\mathbb {Z}}$. More examples were given in [Reference PinkPin98], and many examples are mentioned in [Reference LombardoLom16, § 2.4].
${\rm End}(A)\simeq {\mathbb {Z}}$. More examples were given in [Reference PinkPin98], and many examples are mentioned in [Reference LombardoLom16, § 2.4].
The assumptions of Theorem 1.4 are also satisfied for ‘most’ points in ![]() $S(\overline {{\mathbb {Q}}})$ (with
$S(\overline {{\mathbb {Q}}})$ (with ![]() $S$ of abelian type) in the following sense. The subset consisting of the
$S$ of abelian type) in the following sense. The subset consisting of the ![]() $s\in S(\overline {{\mathbb {Q}}})$ such that
$s\in S(\overline {{\mathbb {Q}}})$ such that ![]() $s$ does not satisfy the Mumford–Tate conjecture is thin in the sense of [Reference SerreSer97, § 9.1]: this uses a combination of [Reference SerreSer94a, § 1], [Reference SerreSer97, § 9] and [Reference Cadoret and MoonenCM20, Theorem A (i)] and Theorem 6.18.
$s$ does not satisfy the Mumford–Tate conjecture is thin in the sense of [Reference SerreSer97, § 9.1]: this uses a combination of [Reference SerreSer94a, § 1], [Reference SerreSer97, § 9] and [Reference Cadoret and MoonenCM20, Theorem A (i)] and Theorem 6.18.
For arbitrary Shimura varieties, the hypotheses of Theorem 1.2 are satisfied in the situation of Theorem 6.18. In a sense, our results apply unconditionally to ‘most’ nonalgebraic points of a Shimura variety. The following are two special cases of Theorem 6.18.
Theorem 1.5 Conjecture 1.1 is true if ![]() $\Sigma$ contains a
$\Sigma$ contains a ![]() $\overline {{\mathbb {Q}}}$-Zariski generic point
$\overline {{\mathbb {Q}}}$-Zariski generic point ![]() $s$ of a special subvariety
$s$ of a special subvariety ![]() $Z\subseteq S$, namely: for every proper subvariety
$Z\subseteq S$, namely: for every proper subvariety ![]() $V\subsetneq Z$ defined over
$V\subsetneq Z$ defined over ![]() $\overline {{\mathbb {Q}}}$, we have
$\overline {{\mathbb {Q}}}$, we have ![]() $s\not \in V({\mathbb {C}})$.
$s\not \in V({\mathbb {C}})$.
Theorem 1.6 Conjecture 1.1 is true if ![]() $M^{\rm ad}$ is
$M^{\rm ad}$ is ![]() ${\mathbb {Q}}$-simple and
${\mathbb {Q}}$-simple and ![]() $\Sigma$ contains a point
$\Sigma$ contains a point ![]() $s$ in
$s$ in ![]() $S({\mathbb {C}})\smallsetminus S(\overline {{\mathbb {Q}}})$.
$S({\mathbb {C}})\smallsetminus S(\overline {{\mathbb {Q}}})$.
1.2 History of Conjecture 1.1
Conjecture 1.1 is a special caseFootnote 1 of the Zilber–Pink conjecture, which has been and continues to be a subject of active research.
Conjecture 1.1 was first formulated (in a special case) in 1989 by André in [Reference AndréAnd89, Chapter X, § 4.5] (Problem 3). Zannier has considered questions of this type in the context of abelian schemes and tori in [Reference ZannierZan12]. It was then stated in the introduction to the second author's 2000 PhD thesis [Reference YafaevYaf00, bottom of p. 12],Footnote 2 following discussions with Bas Edixhoven. Pink, in his 2005 paper [Reference PinkPin05], has formulated and studied this question.
These authors consider the classical HeckeFootnote 3 orbit as in Definition 2.14.
Pink proves the André–Pink–Zannier conjecture for ‘Galois generic’ points of ![]() ${\mathcal {A}}_g$. These points are Hodge generic, by [Reference Cadoret and KretCK16, Proposition 6.2.1]. Pink's method uses equidistribution of Hecke points (by Clozel, Oh, and Ullmo: [Reference Clozel, Ooh and UllmoCOU01]; cf. also [Reference Eskin and OhEO06]). This was generalised to Galois generic points in arbitrary Shimura varieties in 2016 [Reference Cadoret and KretCK16]. This was also contained in the first author's 2009 thesis under a weaker assumption [Reference RichardRic09, Ch. III § 7, p. 59, Corollary 7.1].
${\mathcal {A}}_g$. These points are Hodge generic, by [Reference Cadoret and KretCK16, Proposition 6.2.1]. Pink's method uses equidistribution of Hecke points (by Clozel, Oh, and Ullmo: [Reference Clozel, Ooh and UllmoCOU01]; cf. also [Reference Eskin and OhEO06]). This was generalised to Galois generic points in arbitrary Shimura varieties in 2016 [Reference Cadoret and KretCK16]. This was also contained in the first author's 2009 thesis under a weaker assumption [Reference RichardRic09, Ch. III § 7, p. 59, Corollary 7.1].
In the case of generalisedFootnote 4 Hecke orbits of special points, the articles [Reference Edixhoven and YafaevEY03, Reference Klingler and YafaevKY14] use a method of Edixhoven. This method is inapplicable in more general cases, for instance the case of the Hecke orbit of a Hodge generic point.
A real breakthrough on this problem was the introduction of the Pila–Zannier strategy which uses o-minimality and functional transcendence. It has now become the most powerful approach to all problems of Zilber–Pink type. This method was applied by Orr in [Reference OrrOrr15], who considered the case of curves in ![]() ${\mathcal {A}}_g$, the moduli space of principally polarised abelian varieties. His approach relies on Masser–Wüstholz isogeny estimates. Therefore, it is limited to Shimura varieties of abelian type, and cannot be applied to generalised Hecke orbits. For Shimura varieties of abelian type, Orr was able to prove the conjecture for ‘
${\mathcal {A}}_g$, the moduli space of principally polarised abelian varieties. His approach relies on Masser–Wüstholz isogeny estimates. Therefore, it is limited to Shimura varieties of abelian type, and cannot be applied to generalised Hecke orbits. For Shimura varieties of abelian type, Orr was able to prove the conjecture for ‘![]() $S$-adic Hecke orbits’Footnote 5 for a finite set of primes
$S$-adic Hecke orbits’Footnote 5 for a finite set of primes ![]() $S$, and for points which are Hodge generic (without the Galois generic assumption).
$S$, and for points which are Hodge generic (without the Galois generic assumption).
In the case of ![]() $S$-adic Hecke orbits, a stronger form of the conjecture, involving topological closure and equidistribution, was proved, in the abelian case, in [Reference Richard and YafaevRY19] using ergodic theory approach relying on
$S$-adic Hecke orbits, a stronger form of the conjecture, involving topological closure and equidistribution, was proved, in the abelian case, in [Reference Richard and YafaevRY19] using ergodic theory approach relying on ![]() $p$-adic Ratner's theorems.
$p$-adic Ratner's theorems.
1.3 Main technical results
After choosing bases of the Lie algebras ![]() $\mathfrak {m}$ of
$\mathfrak {m}$ of ![]() $M$ and
$M$ and ![]() $\mathfrak {g}$ of
$\mathfrak {g}$ of ![]() $G$, we associate to
$G$, we associate to ![]() $\phi \in \mbox {Hom}(M,G)$ its ‘finite height’
$\phi \in \mbox {Hom}(M,G)$ its ‘finite height’ ![]() $H_f(\phi )$, defined as the lowest common multiple of the denominators of the coefficients of the matrix of
$H_f(\phi )$, defined as the lowest common multiple of the denominators of the coefficients of the matrix of ![]() $d\phi$. More generally, for
$d\phi$. More generally, for ![]() $g\in G({\mathbb {A}}_f)$, we define
$g\in G({\mathbb {A}}_f)$, we define ![]() $H_f(g^{-1}\cdot \phi \cdot g)$ as the smallest
$H_f(g^{-1}\cdot \phi \cdot g)$ as the smallest ![]() $n\in {\mathbb {Z}}_{\geq 1}$ such that the matrix of
$n\in {\mathbb {Z}}_{\geq 1}$ such that the matrix of ![]() $g^{-1}\cdot d\phi \cdot g$ has coefficients in
$g^{-1}\cdot d\phi \cdot g$ has coefficients in ![]() $({1}/{n})\cdot \widehat {{\mathbb {Z}}}$.
$({1}/{n})\cdot \widehat {{\mathbb {Z}}}$.
1.3.1
A first crucial result is the following. We choose the bases of ![]() $\mathfrak {g}$ and
$\mathfrak {g}$ and ![]() $\mathfrak {m}$ constructed in § 4.3. Then the function
$\mathfrak {m}$ constructed in § 4.3. Then the function
is well defined on the generalised Hecke orbit, and ![]() $Gal(\overline {E}/E)$-invariant.
$Gal(\overline {E}/E)$-invariant.
1.3.2
Our most important technical result is an estimate on the size of Galois orbits in a generalised Hecke orbit.
The following definition is used throughout this article.
Definition 1.7 Let ![]() $A$ be a set and
$A$ be a set and ![]() $f,g:A\to {\mathbb {R}}_{\geq 0}$ two functions.
$f,g:A\to {\mathbb {R}}_{\geq 0}$ two functions.
(i) We say that
 $f$ polynomially dominates
$f$ polynomially dominates  $g$, and write
$g$, and write  $g \preccurlyeq f$, if there exist
$g \preccurlyeq f$, if there exist  $a,b, c \in {\mathbb {R}}_{> 0}$ such that
$a,b, c \in {\mathbb {R}}_{> 0}$ such that
 \[ \forall \, x\in A,\ g(x) \leq c + a f(x)^b. \]
\[ \forall \, x\in A,\ g(x) \leq c + a f(x)^b. \]
(ii) We say that
 $f$ and
$f$ and  $g$ are polynomially equivalent, and write
$g$ are polynomially equivalent, and write  $f \approx g$, if
$f \approx g$, if  $f \preccurlyeq g$ and
$f \preccurlyeq g$ and  $g \preccurlyeq f$.
$g \preccurlyeq f$.
As functions on the generalised Hecke orbit ![]() $\mathcal {H}(s_0)$, we have the polynomial equivalence
$\mathcal {H}(s_0)$, we have the polynomial equivalence
1.3.3
Another essential technical result, from § 5, is the following. See the introduction in § 5 for the importance of this result in our approach to Conjecture 1.1.
Denote by ![]() $\phi _0$ the inclusion monomorphism
$\phi _0$ the inclusion monomorphism ![]() $M\hookrightarrow G$. Let
$M\hookrightarrow G$. Let ![]() $W$ be the conjugacy class
$W$ be the conjugacy class ![]() $G\cdot \phi _0\subseteq \mbox {Hom}(M,G)$, viewed as an algebraic variety over
$G\cdot \phi _0\subseteq \mbox {Hom}(M,G)$, viewed as an algebraic variety over ![]() ${\mathbb {Q}}$. The usual height of the matrix of
${\mathbb {Q}}$. The usual height of the matrix of ![]() $d\phi$ defines an affine Weil height function
$d\phi$ defines an affine Weil height function ![]() $H_W$ on
$H_W$ on ![]() $W({\mathbb {Q}})$ (cf. (15) and (18)). Let
$W({\mathbb {Q}})$ (cf. (15) and (18)). Let ![]() $\mathfrak {S}\subseteq G({\mathbb {R}})$ be a finite union of Siegel sets and
$\mathfrak {S}\subseteq G({\mathbb {R}})$ be a finite union of Siegel sets and ![]() $\mathfrak {S}\cdot \phi _0$ be its image in
$\mathfrak {S}\cdot \phi _0$ be its image in ![]() $W({\mathbb {R}})$.
$W({\mathbb {R}})$.
The main result 5.16 of § 5 is that, as functions of ![]() $\phi \in W({\mathbb {Q}})\cap \mathfrak {S}\cdot \phi _0$, we have
$\phi \in W({\mathbb {Q}})\cap \mathfrak {S}\cdot \phi _0$, we have
We note that every point of the geometric Hecke orbit can be written as ![]() $[\phi \circ x_0,g]$ with
$[\phi \circ x_0,g]$ with ![]() $g\in G({\mathbb {A}}_f)$ and
$g\in G({\mathbb {A}}_f)$ and ![]() $\phi \in W({\mathbb {Q}})\cap \mathfrak {S}\cdot \phi _0$, provided
$\phi \in W({\mathbb {Q}})\cap \mathfrak {S}\cdot \phi _0$, provided ![]() $\mathfrak {S}\subseteq G({\mathbb {R}})$ is a fundamental set.
$\mathfrak {S}\subseteq G({\mathbb {R}})$ is a fundamental set.
1.4 Outline of the strategy
The proof of Theorem 1.2 is given in § 7. The technical results of § 1.3 play a crucial role in our approach. Let us outline our approach.
We reduce Conjecture 1.1 to the case where ![]() $V:=\overline {\Sigma }=\overline {\{s_0;s_1;\ldots \}}$ is irreducible,
$V:=\overline {\Sigma }=\overline {\{s_0;s_1;\ldots \}}$ is irreducible, ![]() $G$ is adjoint and
$G$ is adjoint and ![]() $V$ is Hodge generic in
$V$ is Hodge generic in ![]() $S$. We rely on functoriality properties (§ 2.2) of geometric and generalised Hecke orbits.Footnote 6 Theorem 2.4 allows us to use geometric and generalised Hecke orbits interchangeably. We also rely on the functoriality properties (see § 6.3) of the assumption (1).
$S$. We rely on functoriality properties (§ 2.2) of geometric and generalised Hecke orbits.Footnote 6 Theorem 2.4 allows us to use geometric and generalised Hecke orbits interchangeably. We also rely on the functoriality properties (see § 6.3) of the assumption (1).
The final objective of the proof is to apply the geometric part of the André–Oort conjecture [Reference UllmoUll14] (or [Reference Richard and UllmoRU24]), and use induction on the number of simple factors of ![]() $M^{\rm ad}$. For every
$M^{\rm ad}$. For every ![]() $n$ large enough, we construct a weakly special subvariety
$n$ large enough, we construct a weakly special subvariety ![]() $Z_n\subseteq V$ of non-zero dimension such that
$Z_n\subseteq V$ of non-zero dimension such that ![]() $s_n\in Z_n$. Then [Reference UllmoUll14, Reference Richard and UllmoRU24] describes
$s_n\in Z_n$. Then [Reference UllmoUll14, Reference Richard and UllmoRU24] describes ![]() $\overline {\bigcup Z_n}$, and we deduce Conjecture 1.1.
$\overline {\bigcup Z_n}$, and we deduce Conjecture 1.1.
In order to construct the non-zero-dimensional ![]() $Z_n$, we use the Pila–Zannier strategy. By (3), we identify
$Z_n$, we use the Pila–Zannier strategy. By (3), we identify ![]() $\mathcal {H}(s_0)$ with a subset of
$\mathcal {H}(s_0)$ with a subset of ![]() $W({\mathbb {Q}})$ where
$W({\mathbb {Q}})$ where ![]() $W=G\cdot \phi _0\simeq G/Z_G(M)$ is the algebraic variety of § 1.3.3.
$W=G\cdot \phi _0\simeq G/Z_G(M)$ is the algebraic variety of § 1.3.3.
Let ![]() $\pi :G({\mathbb {R}})\to X\to S$ be the uniformisation map, and
$\pi :G({\mathbb {R}})\to X\to S$ be the uniformisation map, and ![]() $\mathfrak {S}\subseteq G({\mathbb {R}})$ is a finite union of Siegel sets such that
$\mathfrak {S}\subseteq G({\mathbb {R}})$ is a finite union of Siegel sets such that ![]() $S=\pi (\mathfrak {S})$. The goal is to apply the variant Theorem 7.1 of Pila–Wilkie theorem, after constructing many rational points of small height in the set
$S=\pi (\mathfrak {S})$. The goal is to apply the variant Theorem 7.1 of Pila–Wilkie theorem, after constructing many rational points of small height in the set
which is definable in the o-minimal structure ![]() ${\mathbb {R}}_{an,\exp }$.
${\mathbb {R}}_{an,\exp }$.
Let ![]() $E$ be field of definition of
$E$ be field of definition of ![]() $V$. Then
$V$. Then ![]() $V$ contains the Galois orbits
$V$ contains the Galois orbits ![]() $Gal(\overline {E}/E)\cdot s_n$.
$Gal(\overline {E}/E)\cdot s_n$.
We introduce
Denote by ![]() $p$ the map
$p$ the map ![]() $G({\mathbb {R}})\cdot \phi _0\to X$, where
$G({\mathbb {R}})\cdot \phi _0\to X$, where ![]() $G({\mathbb {R}})\cdot \phi _0\subseteq W({\mathbb {R}})$. Each point
$G({\mathbb {R}})\cdot \phi _0\subseteq W({\mathbb {R}})$. Each point ![]() $s'\in Gal(\overline {E}/E)\cdot s_n$ lifts to a rational point
$s'\in Gal(\overline {E}/E)\cdot s_n$ lifts to a rational point ![]() $\widetilde {s'}\in \tilde {V}\cap W({\mathbb {Q}})$. We have surjections
$\widetilde {s'}\in \tilde {V}\cap W({\mathbb {Q}})$. We have surjections ![]() $Q_n\to p(Q_n)\to Gal(\overline {E}/E)\cdot s_n$. Thus,
$Q_n\to p(Q_n)\to Gal(\overline {E}/E)\cdot s_n$. Thus, ![]() $\#Q_n\geq \#Gal(\overline {E}/E)\cdot s_n$.
$\#Q_n\geq \#Gal(\overline {E}/E)\cdot s_n$.
By § 1.3.1, the value of ![]() $H_{f}$ is constant as
$H_{f}$ is constant as ![]() $\phi$ ranges through
$\phi$ ranges through ![]() $Q_n$. By § 1.3.3, we also have
$Q_n$. By § 1.3.3, we also have ![]() $H_f(\phi )\approx H_W(\phi )$. By § 1.3.2, we have
$H_f(\phi )\approx H_W(\phi )$. By § 1.3.2, we have ![]() $\#Q_n\geq \#Gal(\overline {E}/E)\cdot s_n\approx H_f(\widetilde {s_n})\approx H_W(\widetilde {s_n})$.
$\#Q_n\geq \#Gal(\overline {E}/E)\cdot s_n\approx H_f(\widetilde {s_n})\approx H_W(\widetilde {s_n})$.
Thus, ![]() $\tilde {V}$ contains
$\tilde {V}$ contains ![]() $\#Q_n\approx H_W(\widetilde {s_n})$ points of height
$\#Q_n\approx H_W(\widetilde {s_n})$ points of height ![]() $\approx H_W(\widetilde {s_n})$.
$\approx H_W(\widetilde {s_n})$.
By Theorem 7.1, for sufficiently large ![]() $n$, there exist
$n$, there exist ![]() $\phi _n$ in
$\phi _n$ in ![]() $Q_n$ such that
$Q_n$ such that ![]() $p(\phi _n)\in Z^{\rm alg}$, with
$p(\phi _n)\in Z^{\rm alg}$, with ![]() $Z=p(\tilde {V})$. By the Ax–Lindemann–Weierstrass theorem [Reference Klingler, Ullmo and YafaevKUY16], it follows that
$Z=p(\tilde {V})$. By the Ax–Lindemann–Weierstrass theorem [Reference Klingler, Ullmo and YafaevKUY16], it follows that ![]() $s'_n=[\phi _n,1]\in Z_n\subseteq V$, for a non-zero-dimensional weakly special subvariety
$s'_n=[\phi _n,1]\in Z_n\subseteq V$, for a non-zero-dimensional weakly special subvariety ![]() $Z_n$. Using Galois action, we may assume
$Z_n$. Using Galois action, we may assume ![]() $s'_n=s_n$.
$s'_n=s_n$.
This concludes the proof of Theorem 1.2.
1.5 Summary of the sections
In § 2, we introduce and study generalised and geometric Hecke orbits. In § 3, we recall properties of the representations ![]() $\rho _{x_0}:Gal(\overline {E}/E)\to M({\mathbb {A}}_f)$, and we relate Galois orbits to orbits of
$\rho _{x_0}:Gal(\overline {E}/E)\to M({\mathbb {A}}_f)$, and we relate Galois orbits to orbits of ![]() $U=\rho _{x_0}(Gal(\overline {E}/E))$. In § 4, we make precise and prove § 1.3.1. Section 5 deals with § 1.3.2. In § 6, we introduce and study the weakly adelic Mumford–Tate hypothesis, and establish the estimates from § 1.3.3. This relies on general estimates on adelic orbits, given in the appendices. The content of § 7 was outlined in § 1.4.
$U=\rho _{x_0}(Gal(\overline {E}/E))$. In § 4, we make precise and prove § 1.3.1. Section 5 deals with § 1.3.2. In § 6, we introduce and study the weakly adelic Mumford–Tate hypothesis, and establish the estimates from § 1.3.3. This relies on general estimates on adelic orbits, given in the appendices. The content of § 7 was outlined in § 1.4.
2. Generalised and geometric Hecke orbits
In this section we define the notions of generalised Hecke orbit and of geometric Hecke orbit, and study their properties. The heart of this section is Theorem 2.4, which implies, in particular, that generalised and geometric Hecke orbits can be used interchangeably in the statement of Conjecture 1.1.
These notions are naturally compatible with various operations on Shimura data. In particular, we prove several statements which will be important in reducing Conjecture 1.1 to the case where the Shimura variety is of adjoint type and ![]() $\Sigma$ is Hodge generic in
$\Sigma$ is Hodge generic in ![]() $S$.
$S$.
Finally, § 2.5 compares our notions to different notions of generalised Hecke orbits found in the literature.
2.1 Definitions
Let ![]() $(G,X)$ be a Shimura datum. We always assume, as in [Reference Ullmo and YafaevUY14], that our Shimura datum is normalised so that
$(G,X)$ be a Shimura datum. We always assume, as in [Reference Ullmo and YafaevUY14], that our Shimura datum is normalised so that ![]() $G$ is the generic Mumford–Tate group of
$G$ is the generic Mumford–Tate group of ![]() $X$.
$X$.
Let ![]() $x_0$ be a point of
$x_0$ be a point of ![]() $X$ and let
$X$ and let ![]() $M \leq G$ be the Mumford–Tate group of
$M \leq G$ be the Mumford–Tate group of ![]() $x_0$. Recall that
$x_0$. Recall that ![]() $x_0$ is a morphism
$x_0$ is a morphism ![]() ${\mathbb {S}} :=\operatorname {Res}_{{\mathbb {C}}/{\mathbb {R}}}(GL(1))\longrightarrow G_{{\mathbb {R}}}$ and that
${\mathbb {S}} :=\operatorname {Res}_{{\mathbb {C}}/{\mathbb {R}}}(GL(1))\longrightarrow G_{{\mathbb {R}}}$ and that ![]() $M = x_0({\mathbb {S}})^{Zar, {\mathbb {Q}}}$ is the smallest
$M = x_0({\mathbb {S}})^{Zar, {\mathbb {Q}}}$ is the smallest ![]() ${\mathbb {Q}}$-algebraic subgroup of
${\mathbb {Q}}$-algebraic subgroup of ![]() $G$ containing
$G$ containing ![]() $x_0({\mathbb {S}})$. In the rest of the paper we denote the identity monomorphism
$x_0({\mathbb {S}})$. In the rest of the paper we denote the identity monomorphism ![]() $M \hookrightarrow G$ by
$M \hookrightarrow G$ by ![]() $\phi _0$.
$\phi _0$.
In the following definition ![]() $\mbox {Hom}(M,G)$ denotes the set of algebraic group morphisms defined over
$\mbox {Hom}(M,G)$ denotes the set of algebraic group morphisms defined over ![]() ${\mathbb {Q}}$.
${\mathbb {Q}}$.
Definition 2.1 (Generalised Hecke orbit)
We define the Generalised Hecke orbit ![]() $\mathcal {H}(x_0)$ of
$\mathcal {H}(x_0)$ of ![]() $x_0$ in
$x_0$ in ![]() $X$ as
$X$ as
Let ![]() $X_M=M({\mathbb {R}})\cdot x_0\subset X$. Then
$X_M=M({\mathbb {R}})\cdot x_0\subset X$. Then ![]() $(M,X_M)$ is a Shimura datum, and
$(M,X_M)$ is a Shimura datum, and ![]() $\phi \in \mbox {Hom}(M,G)$ such that
$\phi \in \mbox {Hom}(M,G)$ such that ![]() $\phi \circ x_0\in X$ are precisely those giving rise to a morphism of Shimura data
$\phi \circ x_0\in X$ are precisely those giving rise to a morphism of Shimura data ![]() $(M,X_M)\to (G,X)$. In particular,
$(M,X_M)\to (G,X)$. In particular, ![]() $\phi (X_M)\subseteq X$.
$\phi (X_M)\subseteq X$.
Let ![]() $K$ be a compact open subgroup of
$K$ be a compact open subgroup of ![]() $G({\mathbb {A}}_f)$ and
$G({\mathbb {A}}_f)$ and ![]() ${\rm Sh}_K(G,X)$ be the Shimura variety associated to these data. There is a natural map
${\rm Sh}_K(G,X)$ be the Shimura variety associated to these data. There is a natural map
and we denote the image of a point ![]() $(x,g)$ by
$(x,g)$ by ![]() $[x,g]$.
$[x,g]$.
Definition 2.2 We define the generalised Hecke orbit ![]() $\mathcal {H}([x_0, g_0])$ of
$\mathcal {H}([x_0, g_0])$ of ![]() $[x_0, g_0]$ in
$[x_0, g_0]$ in ![]() ${\rm Sh}_K(G,X)$ by
${\rm Sh}_K(G,X)$ by
Let ![]() $W=G\cdot \phi _0$ be the conjugacy class of
$W=G\cdot \phi _0$ be the conjugacy class of ![]() $\phi _0$ which we view as an algebraic variety defined over
$\phi _0$ which we view as an algebraic variety defined over ![]() ${\mathbb {Q}}$. Denoting by
${\mathbb {Q}}$. Denoting by ![]() $Z_G(M)$ the centraliser of
$Z_G(M)$ the centraliser of ![]() $M$ in
$M$ in ![]() $G$, we will identify
$G$, we will identify ![]() $G/Z_G(M)\simeq W$. The set
$G/Z_G(M)\simeq W$. The set ![]() $W(\overline {{\mathbb {Q}}})$ is the
$W(\overline {{\mathbb {Q}}})$ is the ![]() $G(\overline {{\mathbb {Q}}})$-conjugacy class of
$G(\overline {{\mathbb {Q}}})$-conjugacy class of ![]() $\phi _0$ in
$\phi _0$ in ![]() $\mbox {Hom}(M_{\overline {{\mathbb {Q}}}},G_{\overline {{\mathbb {Q}}}})$, and the points in
$\mbox {Hom}(M_{\overline {{\mathbb {Q}}}},G_{\overline {{\mathbb {Q}}}})$, and the points in ![]() $W({\mathbb {Q}})$ are the
$W({\mathbb {Q}})$ are the ![]() ${\mathbb {Q}}$-defined homomorphisms
${\mathbb {Q}}$-defined homomorphisms ![]() $\phi \in \mbox {Hom}(M,G)$ which are conjugated to
$\phi \in \mbox {Hom}(M,G)$ which are conjugated to ![]() $\phi _0$ by elements of
$\phi _0$ by elements of ![]() $G(\overline {{\mathbb {Q}}})$.
$G(\overline {{\mathbb {Q}}})$.
In Definition 2.1, if we replace ![]() $\mbox {Hom}(M,G)$ by its subset
$\mbox {Hom}(M,G)$ by its subset ![]() $W({\mathbb {Q}})$, we obtain a more restrictive definition: that of a geometric Hecke orbit.
$W({\mathbb {Q}})$, we obtain a more restrictive definition: that of a geometric Hecke orbit.
Definition 2.3 We define the geometric Hecke orbit ![]() $\mathcal {H}^g(x_0)$ of
$\mathcal {H}^g(x_0)$ of ![]() $x_0$ by
$x_0$ by
and the geometric Hecke orbit of ![]() $[x_0,g_0]$ by
$[x_0,g_0]$ by
The main result of this section is the following.
Theorem 2.4 The generalised Hecke orbit ![]() $\mathcal {H}(x_0)$ is a union of finitely many geometric Hecke orbits.
$\mathcal {H}(x_0)$ is a union of finitely many geometric Hecke orbits.
Lemma 2.5 Let ![]() $\phi,\phi '\in \mbox {Hom}(M,G)$ (defined over
$\phi,\phi '\in \mbox {Hom}(M,G)$ (defined over ![]() ${\mathbb {Q}}$) be such that
${\mathbb {Q}}$) be such that ![]() $\phi \circ x_0=\phi '\circ x_0$.
$\phi \circ x_0=\phi '\circ x_0$.
Then ![]() $\phi =\phi '$.
$\phi =\phi '$.
Proof. One can check directly that
is a subgroup of ![]() $M({\mathbb {C}})$ (it is the ‘equaliser’ of
$M({\mathbb {C}})$ (it is the ‘equaliser’ of ![]() $\phi$ and
$\phi$ and ![]() $\phi '$). It is algebraic and defined over
$\phi '$). It is algebraic and defined over ![]() ${\mathbb {Q}}$ because
${\mathbb {Q}}$ because ![]() $\phi$ and
$\phi$ and ![]() $\phi '$ are. It contains the image
$\phi '$ are. It contains the image ![]() $x_0({\mathbb {C}})$ by hypothesis. But
$x_0({\mathbb {C}})$ by hypothesis. But ![]() $M$ is the Mumford–Tate group of
$M$ is the Mumford–Tate group of ![]() $x_0$: there is no proper
$x_0$: there is no proper ![]() ${\mathbb {Q}}$-algebraic subgroup of
${\mathbb {Q}}$-algebraic subgroup of ![]() $M$ containing
$M$ containing ![]() $x_0({\mathbb {C}})$. Therefore,
$x_0({\mathbb {C}})$. Therefore, ![]() $H=M$. Thus,
$H=M$. Thus, ![]() $\phi =\phi '$.
$\phi =\phi '$.
The algebraic variety ![]() $W$ is our central object in this article. We will use the notation
$W$ is our central object in this article. We will use the notation
and
The subset ![]() $W({\mathbb {R}})^+\subset W({\mathbb {R}})$ is a union of some connected components of
$W({\mathbb {R}})^+\subset W({\mathbb {R}})$ is a union of some connected components of ![]() $W({\mathbb {R}})$. With this notation, Lemma 2.5 implies that we have a bijection
$W({\mathbb {R}})$. With this notation, Lemma 2.5 implies that we have a bijection
2.2 Functoriality of generalised and geometric Hecke orbits
2.2.1 Restriction to special subvarieties
The following is a set-theoretic tautology.
Proposition 2.6 Let ![]() $(G',X')$ be a Shimura datum with
$(G',X')$ be a Shimura datum with ![]() $M\leq G'\leq G$ and
$M\leq G'\leq G$ and ![]() $X_M\subset X'\subset X$, and define
$X_M\subset X'\subset X$, and define ![]() $K'=G'({\mathbb {A}}_f)\cap K$.
$K'=G'({\mathbb {A}}_f)\cap K$.
(i) Let
 $\mathcal {H}'(x_0)$ be the generalised Hecke orbit of
$\mathcal {H}'(x_0)$ be the generalised Hecke orbit of  $x_0$ viewed as a point of
$x_0$ viewed as a point of  $X'$.
$X'$.Then
 \[ \mathcal{H}'(x_0)= \mathcal{H}(x_0)\cap X'. \]
\[ \mathcal{H}'(x_0)= \mathcal{H}(x_0)\cap X'. \]
(ii) Let
 $\mathcal {H}'([x_0,1])$ be the generalised Hecke orbit of
$\mathcal {H}'([x_0,1])$ be the generalised Hecke orbit of  $[x_0,1]$ viewed as a point of
$[x_0,1]$ viewed as a point of  $Sh_{K'}(G',X')$, and
$Sh_{K'}(G',X')$, and  $S'$ the image of
where
$S'$ the image of
where \[ f:=Sh(\iota):Sh_{K'}(G',X')\to Sh_{K}(G,X) \]
\[ f:=Sh(\iota):Sh_{K'}(G',X')\to Sh_{K}(G,X) \]
 $\iota :G'\to G$ is the inclusion. Then
$\iota :G'\to G$ is the inclusion. Then
 \[ \mathcal{H}([x_0,1])\cap S' = f(\mathcal{H}'([x_0,1]))\text{ and }\mathcal{H}'([x_0,1]) =\stackrel{-1}{f}(\mathcal{H}([x_0,1])). \]
\[ \mathcal{H}([x_0,1])\cap S' = f(\mathcal{H}'([x_0,1]))\text{ and }\mathcal{H}'([x_0,1]) =\stackrel{-1}{f}(\mathcal{H}([x_0,1])). \]
The following corollary can be deduced by combining Lemma 2.5 with Theorem 2.4 (it can also be deduced from [Reference RichardsonRic67]).
Corollary 2.7 We keep previous notation. Then
is a finite union of geometric Hecke orbits in ![]() $X'$.
$X'$.
Accordingly, ![]() $\stackrel {-1}{f}(\mathcal {H}^g([x_0,1]))$ is the image of finitely many geometric Hecke orbits in
$\stackrel {-1}{f}(\mathcal {H}^g([x_0,1]))$ is the image of finitely many geometric Hecke orbits in ![]() $Sh_{K'}(G',X')$.
$Sh_{K'}(G',X')$.
2.2.2 Compatibility to products
A useful property of geometric Hecke orbits is the compatibility with respect to products of Shimura data.
Lemma 2.8 Let ![]() $(G,X)$ be an adjoint Shimura datum, and factor
$(G,X)$ be an adjoint Shimura datum, and factor ![]() $G=G_1\times \cdots \times G_f$ as a product of its
$G=G_1\times \cdots \times G_f$ as a product of its ![]() ${\mathbb {Q}}$-defined simple normal subgroups, and assume
${\mathbb {Q}}$-defined simple normal subgroups, and assume ![]() $K=K_1\times \cdots \times K_f$ for compact open subgroups
$K=K_1\times \cdots \times K_f$ for compact open subgroups ![]() $K_i\leq G_i({\mathbb {A}}_f)$. We use
$K_i\leq G_i({\mathbb {A}}_f)$. We use ![]() $X=X_1\times \cdots \times X_f$ to denote the corresponding factorisation, and choose
$X=X_1\times \cdots \times X_f$ to denote the corresponding factorisation, and choose ![]() $x_0= (x_1,\ldots,x_f)\in X_1\times \cdots \times X_f$. We use
$x_0= (x_1,\ldots,x_f)\in X_1\times \cdots \times X_f$. We use ![]() $\mathcal {H}^g(x_i)$ to denote the geometric Hecke orbit of
$\mathcal {H}^g(x_i)$ to denote the geometric Hecke orbit of ![]() $x_i$ with respect to the Shimura datum
$x_i$ with respect to the Shimura datum ![]() $(G_i,X_i)$.
$(G_i,X_i)$.
With respect to the corresponding factorisation of Shimura varieties
we have
It follows from Lemma 2.8 that, at the level of Shimura varieties,
Proof. Since ![]() $G$ is adjoint, we have a factorisation
$G$ is adjoint, we have a factorisation
Let ![]() $M$ be the Mumford–Tate group of
$M$ be the Mumford–Tate group of ![]() $x_0$ and let
$x_0$ and let ![]() $\phi _0=(\phi _1,\ldots,\phi _f):M\to G=G_1\times \cdots \times G_f$ be the inclusion. As the conjugacy class in a product is the product of conjugacy classes, we have
$\phi _0=(\phi _1,\ldots,\phi _f):M\to G=G_1\times \cdots \times G_f$ be the inclusion. As the conjugacy class in a product is the product of conjugacy classes, we have
The Mumford–Tate group of ![]() $x_i$ is
$x_i$ is ![]() $M_i:=\phi _i(M)$. Because
$M_i:=\phi _i(M)$. Because ![]() $x_0({\mathbb {S}})$ is Zariski dense over
$x_0({\mathbb {S}})$ is Zariski dense over ![]() ${\mathbb {Q}}$ in
${\mathbb {Q}}$ in ![]() $M$ so is
$M$ so is ![]() $x_i({\mathbb {S}})$ in
$x_i({\mathbb {S}})$ in ![]() $M_i$. Let
$M_i$. Let ![]() $\phi _i':M_i\to G_i$ be the identity map. We can identify
$\phi _i':M_i\to G_i$ be the identity map. We can identify ![]() $G_i\cdot \phi _i\simeq G_i\cdot \phi '_i$, and have
$G_i\cdot \phi _i\simeq G_i\cdot \phi '_i$, and have
The rest follows from the definition of geometric Hecke orbits.
2.2.3 Passing to the adjoint Shimura datum
The following property is used to reduce the proof of Conjecture 1.1 and Theorem 1.2 to the case where ![]() $G$ is adjoint.
$G$ is adjoint.
Lemma 2.9 Let ![]() $ad:(G,X)\to (G^{\rm ad},X^{\rm ad})$ be the map of Shimura dataFootnote 7 induced by the natural morphism
$ad:(G,X)\to (G^{\rm ad},X^{\rm ad})$ be the map of Shimura dataFootnote 7 induced by the natural morphism ![]() $ad:G\to G^{\rm ad}$ and choose a compact open subgroup
$ad:G\to G^{\rm ad}$ and choose a compact open subgroup ![]() $K^{\rm ad}\leq G^{\rm ad}({\mathbb {A}}_f)$ containing
$K^{\rm ad}\leq G^{\rm ad}({\mathbb {A}}_f)$ containing ![]() $ad(K)$. Let
$ad(K)$. Let ![]() $ad:x\mapsto x^{\rm ad}:=ad\circ x$ be the map
$ad:x\mapsto x^{\rm ad}:=ad\circ x$ be the map ![]() $X\to X^{\rm ad}$ and
$X\to X^{\rm ad}$ and
the corresponding morphism of Shimura varieties.
Let ![]() $x_0\in X$. Recall that
$x_0\in X$. Recall that ![]() $\mathcal {H}^g(x_0)$ and
$\mathcal {H}^g(x_0)$ and ![]() $\mathcal {H}^g(x_0^{\rm ad})$ denote the geometric Hecke orbit of
$\mathcal {H}^g(x_0^{\rm ad})$ denote the geometric Hecke orbit of ![]() $x_0$ and
$x_0$ and ![]() $x_0^{\rm ad}$ with respect to
$x_0^{\rm ad}$ with respect to ![]() $G$ and
$G$ and ![]() $G^{\rm ad}$.
$G^{\rm ad}$.
We have
Lemma 2.9 implies the inclusion
Passing to the quotient, we obtain the following.
Corollary 2.10 We have ![]() $Sh(ad)(\mathcal {H}^g([x_0,1]))\subseteq \mathcal {H}^g([x_0^{\rm ad},1]).$
$Sh(ad)(\mathcal {H}^g([x_0,1]))\subseteq \mathcal {H}^g([x_0^{\rm ad},1]).$
We now prove Lemma 2.9.
Proof. Choose ![]() $x\in \mathcal {H}^g(x_0)$. Clearly
$x\in \mathcal {H}^g(x_0)$. Clearly ![]() $x':=ad(x) \in ad(X) \subset X^{\rm ad}$.
$x':=ad(x) \in ad(X) \subset X^{\rm ad}$.
The Mumford–Tate group of ![]() $x'_0:=ad(x_0)$ is
$x'_0:=ad(x_0)$ is ![]() $M':=ad(M)$. We denote by
$M':=ad(M)$. We denote by ![]() $\phi _0' \colon M' \to G^{\rm ad}$ the natural injection. We can write
$\phi _0' \colon M' \to G^{\rm ad}$ the natural injection. We can write ![]() $x=\phi \circ x_0$ with
$x=\phi \circ x_0$ with ![]() $\phi = g \phi _0 g^{-1}$ and
$\phi = g \phi _0 g^{-1}$ and ![]() $g \in G(\overline {{\mathbb {Q}}})$. Then
$g \in G(\overline {{\mathbb {Q}}})$. Then ![]() $\phi ' := ad(g) \phi '_0 ad(g)^{-1}$ is defined over
$\phi ' := ad(g) \phi '_0 ad(g)^{-1}$ is defined over ![]() ${\mathbb {Q}}$ because the map
${\mathbb {Q}}$ because the map ![]() $G \cdot \phi _0\to G^{\rm ad} \cdot \phi '_0$ between conjugacy classes is a morphism of varieties defined over
$G \cdot \phi _0\to G^{\rm ad} \cdot \phi '_0$ between conjugacy classes is a morphism of varieties defined over ![]() ${\mathbb {Q}}$. One computes
${\mathbb {Q}}$. One computes ![]() $x'=ad(gx_0g^{-1})=ad(g)ad(x_0)ad(g)^{-1}=\phi '\circ x_0'$, where
$x'=ad(gx_0g^{-1})=ad(g)ad(x_0)ad(g)^{-1}=\phi '\circ x_0'$, where ![]() $x_0'\in X^{\rm ad}$, and
$x_0'\in X^{\rm ad}$, and ![]() $\phi$ is defined over
$\phi$ is defined over ![]() ${\mathbb {Q}}$ and conjugated to
${\mathbb {Q}}$ and conjugated to ![]() $\phi _0'$ over
$\phi _0'$ over ![]() $\overline {{\mathbb {Q}}}$; that is,
$\overline {{\mathbb {Q}}}$; that is, ![]() $x'\in \mathcal {H}^g(x_0')$.
$x'\in \mathcal {H}^g(x_0')$.
Remarks
In (4), the reverse inclusion is also true, but it is not used in this paper, and its proof is left to the interested reader. The inclusion (4) and the proof we have given also applies to general morphisms of Shimura data ![]() $(G,X)\to (G',X')$ instead of just
$(G,X)\to (G',X')$ instead of just ![]() $(G,X)\to (G^{\rm ad},X^{\rm ad})$.
$(G,X)\to (G^{\rm ad},X^{\rm ad})$.
2.3 Rational conjugacy of linear representations
The following notable fact will be used at several places in this article. We believe this property is also of independent interest.
Theorem 2.11 [Reference Borel and TitsBT65, § 12.3, third paragraph]
For any algebraic group ![]() $M$ over
$M$ over ![]() ${\mathbb {Q}}$, any two representations
${\mathbb {Q}}$, any two representations ![]() $\phi,\phi ':M\to GL(n)$ which are defined over
$\phi,\phi ':M\to GL(n)$ which are defined over ![]() ${\mathbb {Q}}$ and conjugated under
${\mathbb {Q}}$ and conjugated under ![]() $GL(n,\overline {{\mathbb {Q}}})$ are actually conjugated under
$GL(n,\overline {{\mathbb {Q}}})$ are actually conjugated under ![]() $GL(n,{\mathbb {Q}})$.
$GL(n,{\mathbb {Q}})$.
It follows from the theory of linear representations for which references are for example [Reference HumphreysHum75, Chapter XI] for ![]() $\overline {{\mathbb {Q}}}$ and [Reference Borel and TitsBT65, § 12] over
$\overline {{\mathbb {Q}}}$ and [Reference Borel and TitsBT65, § 12] over ![]() ${\mathbb {Q}}$. We will only need the case where
${\mathbb {Q}}$. We will only need the case where ![]() $M$ is connected and reductive, and this case can be found, for instance, in [Reference Borel and TitsBT65, § 12.3, third paragraph]. They give a Galois cohomology argument, and the same Galois cohomology argument works in general with a reference to [Reference KneserKne69, 1.7 Example 1, p. 16] instead. For reductive groups, it is also possible to reduce the result to Skolem–Noether theorem. For tori, it can be reduced to the fact that any matrix is rationally conjugated to its canonical companion form.
$M$ is connected and reductive, and this case can be found, for instance, in [Reference Borel and TitsBT65, § 12.3, third paragraph]. They give a Galois cohomology argument, and the same Galois cohomology argument works in general with a reference to [Reference KneserKne69, 1.7 Example 1, p. 16] instead. For reductive groups, it is also possible to reduce the result to Skolem–Noether theorem. For tori, it can be reduced to the fact that any matrix is rationally conjugated to its canonical companion form.
2.4 Proof of the finiteness Theorem 2.4
The strategy will combine an argument for semisimple groups and another for algebraic tori.
Proposition 2.12 Let ![]() $M$ be a semisimple algebraic group over
$M$ be a semisimple algebraic group over ![]() ${\mathbb {Q}}$ (respectively,
${\mathbb {Q}}$ (respectively, ![]() $\overline {{\mathbb {Q}}}$).
$\overline {{\mathbb {Q}}}$).
(i) For all
 $d\in {\mathbb {Z}}_{\geq 0}$, the set of linear representations defined over
$d\in {\mathbb {Z}}_{\geq 0}$, the set of linear representations defined over  ${\mathbb {Q}}$ (respectively,
${\mathbb {Q}}$ (respectively,  $\overline {{\mathbb {Q}}}$)
is a finite union of conjugacy classes under
$\overline {{\mathbb {Q}}}$)
is a finite union of conjugacy classes under \[ \mbox{Hom}(M,GL(d)) \]
\[ \mbox{Hom}(M,GL(d)) \]
 $GL(d,{\mathbb {Q}})$ (respectively, under
$GL(d,{\mathbb {Q}})$ (respectively, under  $GL(d,\overline {{\mathbb {Q}}})$.)
$GL(d,\overline {{\mathbb {Q}}})$.)(ii) Let
 $G$ be a reductive linear algebraic group over
$G$ be a reductive linear algebraic group over  ${\mathbb {Q}}$ (respectively,
${\mathbb {Q}}$ (respectively,  $\overline {{\mathbb {Q}}}$). Then the set of homomorphisms defined over
$\overline {{\mathbb {Q}}}$). Then the set of homomorphisms defined over  ${\mathbb {Q}}$ (respectively,
${\mathbb {Q}}$ (respectively,  $\overline {{\mathbb {Q}}}$)
is contained in (respectively, is equal to) a finite union of
$\overline {{\mathbb {Q}}}$)
is contained in (respectively, is equal to) a finite union of \[ \mbox{Hom}(M,G) \]
\[ \mbox{Hom}(M,G) \]
 $G(\overline {{\mathbb {Q}}})$-conjugacy classes.
$G(\overline {{\mathbb {Q}}})$-conjugacy classes.
For simplicity, we will only give an argument which assumes ![]() $M$ is Zariski connected, which is the case considered in the proof of Theorem 2.4.
$M$ is Zariski connected, which is the case considered in the proof of Theorem 2.4.
Proof. We prove the first assertion. By virtue of Theorem 2.11, it is enough to treat the case where everything is defined over ![]() $\overline {{\mathbb {Q}}}$.
$\overline {{\mathbb {Q}}}$.
Because ![]() $M$ is connected it is enough to prove that there are finitely many conjugacy classes of Lie algebra representations
$M$ is connected it is enough to prove that there are finitely many conjugacy classes of Lie algebra representations ![]() $\mathfrak {m}\to \mathfrak {gl}(d)$. Equivalently, there are finitely many isomorphisms classes of linear representations of
$\mathfrak {m}\to \mathfrak {gl}(d)$. Equivalently, there are finitely many isomorphisms classes of linear representations of ![]() $\mathfrak {m}$ of dimension
$\mathfrak {m}$ of dimension ![]() $d$. For this,Footnote 8 we refer to [Reference HallHal03, § 7].
$d$. For this,Footnote 8 we refer to [Reference HallHal03, § 7].
For the second assertion we treat the case where everything is defined over ![]() $\overline {{\mathbb {Q}}}$, which implies the case where everything is defined over
$\overline {{\mathbb {Q}}}$, which implies the case where everything is defined over ![]() ${\mathbb {Q}}$. It is deduced from the first part by using [Reference RichardsonRic67, Theorem 3.1].
${\mathbb {Q}}$. It is deduced from the first part by using [Reference RichardsonRic67, Theorem 3.1].
We prove Theorem 2.4 combining [Reference Ullmo and YafaevUY14, Lemma 2.6] with Proposition 2.13.
Proof. We identify ![]() $G$ with its image by a faithful representation
$G$ with its image by a faithful representation ![]() $G\to GL(d)$, and we let
$G\to GL(d)$, and we let ![]() $\Sigma =\{\phi \in \mbox {Hom}(M,G):\phi \circ x_0\in X\}$.
$\Sigma =\{\phi \in \mbox {Hom}(M,G):\phi \circ x_0\in X\}$.
ThanksFootnote 9 to [Reference Ullmo and YafaevUY14, Lemma 2.6], we may use Proposition 2.13, and deduce that ![]() $\Sigma =\{\phi \in \mbox {Hom}(M,G):\phi \circ x_0\in X\}$ is contained in finitely many
$\Sigma =\{\phi \in \mbox {Hom}(M,G):\phi \circ x_0\in X\}$ is contained in finitely many ![]() $GL(d)$-conjugacy classes. Using [Reference RichardsonRic67], we conclude that
$GL(d)$-conjugacy classes. Using [Reference RichardsonRic67], we conclude that ![]() $\Sigma$ is contained in finitely many
$\Sigma$ is contained in finitely many ![]() $G(\overline {{\mathbb {Q}}})$-conjugacy classes, thus proving Theorem 2.4.
$G(\overline {{\mathbb {Q}}})$-conjugacy classes, thus proving Theorem 2.4.
Proposition 2.13 (Bounding conjugacy classes)
Let ![]() $M$ be a connected reductive
$M$ be a connected reductive ![]() $\overline {{\mathbb {Q}}}$-group,
$\overline {{\mathbb {Q}}}$-group, ![]() $M^{\rm der}$ its derived subgroup and
$M^{\rm der}$ its derived subgroup and ![]() $T=Z_M(M)^0$ its connected centre.
$T=Z_M(M)^0$ its connected centre.
A subset ![]() $\Sigma \subseteq \mbox {Hom}(M,GL(d))$ is contained in finitely many
$\Sigma \subseteq \mbox {Hom}(M,GL(d))$ is contained in finitely many ![]() $GL(d)$-conjugacy classes if and only if: there is a finite set of characters
$GL(d)$-conjugacy classes if and only if: there is a finite set of characters ![]() $F\subset X(T)$ such that for every
$F\subset X(T)$ such that for every ![]() $\rho \in \Sigma$, all the weights of the representation
$\rho \in \Sigma$, all the weights of the representation ![]() $\rho \restriction _T:T\to GL(d)$ belong to
$\rho \restriction _T:T\to GL(d)$ belong to ![]() $F$.
$F$.
Proof. Because the set of characters is invariant under conjugation, the condition is necessary. We prove that this condition is also sufficient.
We know that two representations of a torus ![]() $T$ are conjugated if and only if they have the same weights, with same multiplicities. As the weights belongs to
$T$ are conjugated if and only if they have the same weights, with same multiplicities. As the weights belongs to ![]() $F$, and the dimension
$F$, and the dimension ![]() $d$ is fixed, there are only finitely many possibilities for these weights and multiplicities. Hence,
$d$ is fixed, there are only finitely many possibilities for these weights and multiplicities. Hence, ![]() $\{\rho \restriction _T:\rho \in \Sigma \}$ is contained in at most finitely many conjugacy classes
$\{\rho \restriction _T:\rho \in \Sigma \}$ is contained in at most finitely many conjugacy classes ![]() $GL(d)\cdot \rho _1\restriction _T,\ldots,GL(d)\cdot \rho _c\restriction _T$. Without loss of generality we may assume that there is only one conjugacy class, say
$GL(d)\cdot \rho _1\restriction _T,\ldots,GL(d)\cdot \rho _c\restriction _T$. Without loss of generality we may assume that there is only one conjugacy class, say ![]() $GL(d)\cdot \rho _{1}\restriction _{T}$.
$GL(d)\cdot \rho _{1}\restriction _{T}$.
We want to prove that
Possibly after conjugating, we may assume ![]() $\rho \restriction _T=\rho _1\restriction _T$. Because
$\rho \restriction _T=\rho _1\restriction _T$. Because ![]() $M$ is connected, one has
$M$ is connected, one has ![]() $M=M^{\rm der}\cdot T$. Thus,
$M=M^{\rm der}\cdot T$. Thus,
As ![]() $M^{\rm der}$ and
$M^{\rm der}$ and ![]() $T$ commute with each other,
$T$ commute with each other, ![]() $\rho \restriction _{M^{\rm der}}:M^{\rm der}\to GL(d)$ factors through
$\rho \restriction _{M^{\rm der}}:M^{\rm der}\to GL(d)$ factors through ![]() $G':=Z_{GL(d)}(\rho _1(T))$. As
$G':=Z_{GL(d)}(\rho _1(T))$. As ![]() $T$ is reductive, so is
$T$ is reductive, so is ![]() $G'$.
$G'$.
By Proposition 2.12, these ![]() $\rho \restriction _{M^{\rm der}}$ belong to finitely many conjugacy classes
$\rho \restriction _{M^{\rm der}}$ belong to finitely many conjugacy classes ![]() $G'\cdot \rho _{1,1}\restriction _{M^{\rm der}} ,\ldots,G'\cdot \rho _{1,e}\restriction _{M^{\rm der}}$. Possibly after conjugating
$G'\cdot \rho _{1,1}\restriction _{M^{\rm der}} ,\ldots,G'\cdot \rho _{1,e}\restriction _{M^{\rm der}}$. Possibly after conjugating ![]() $\rho$ by some
$\rho$ by some ![]() $g\in G'$, which does not change
$g\in G'$, which does not change ![]() $\rho \restriction _T$, we have
$\rho \restriction _T$, we have
In light of (6), this proves (5) and the conclusion follows.
2.5 Relation to other notions of Hecke orbits
The following is not used in the rest of this article, however it clarifies the relation between different notions of Hecke orbits and we believe it to be of independent interest. We compare our generalised and geometric Hecke orbits to the classical Hecke orbits and another notion of ‘generalised Hecke’ orbit found in the literature.
2.5.1 Relation to the classical definition of Hecke orbit
Let us recall the notion of the classical Hecke orbit.
Definition 2.14 (classical Hecke orbit)
Define the classical Hecke orbit of ![]() $x_0$ as follows:
$x_0$ as follows:
and the classical Hecke orbit of ![]() $[x_0,1]$ as
$[x_0,1]$ as
We have a chain of inclusions:
In general, ![]() $\mathcal {H}^g(x_0)$ is not a finite union of classical Hecke orbits, even when
$\mathcal {H}^g(x_0)$ is not a finite union of classical Hecke orbits, even when ![]() $G$ is of adjoint type.
$G$ is of adjoint type.
Hecke correspondences
Recall that the classical Hecke orbit can be described using Hecke correspondences. For ![]() $g\in G({\mathbb {Q}})$, the points
$g\in G({\mathbb {Q}})$, the points ![]() $s_0=[x_0,1]$ and
$s_0=[x_0,1]$ and ![]() $s_g=[g\cdot x_0,1]$ have a common inverse image by the left, respectively, right, finite map in
$s_g=[g\cdot x_0,1]$ have a common inverse image by the left, respectively, right, finite map in
where ![]() $Sh(Ad_g)$ the right map is the Shimura morphism associated to the map of Shimura data
$Sh(Ad_g)$ the right map is the Shimura morphism associated to the map of Shimura data ![]() $AD_g:(G,X)\to (G,X)$ induced by the conjugation
$AD_g:(G,X)\to (G,X)$ induced by the conjugation ![]() $AD_g:G\to G$ and
$AD_g:G\to G$ and ![]() $Sh(Ad_1)$ is induced by the identity map
$Sh(Ad_1)$ is induced by the identity map ![]() $AD_1:G\to G$.
$AD_1:G\to G$.
Likewise generalised Hecke orbits can be interpreted using finite correspondences between Shimura varieties. For a point ![]() $\phi \circ x_0\in \mathcal {H}(x_0)$, the point
$\phi \circ x_0\in \mathcal {H}(x_0)$, the point ![]() $s_0$ and
$s_0$ and ![]() $s_\phi =[\phi \circ x_0,1]$ have a common inverse image in
$s_\phi =[\phi \circ x_0,1]$ have a common inverse image in
This time the correspondence is induced by a correspondence from the image of ![]() $Sh(\phi _0)$ to that of
$Sh(\phi _0)$ to that of ![]() $Sh(\phi )$. These are also the smallest special subvarieties containing
$Sh(\phi )$. These are also the smallest special subvarieties containing ![]() $s_0$, respectively,
$s_0$, respectively, ![]() $s_\phi$.
$s_\phi$.
2.5.2 Relation to the usual definition of the generalised Hecke orbit
We compare our notion of generalised Hecke to the ‘generalised Hecke orbits’ used in [Reference Klingler and YafaevKY14] and [Reference Edixhoven and YafaevEY03, Reference PinkPin05, Reference OrrOrr15, Reference Ullmo and YafaevUY13]. The latter is defined in terms of linear representations.
For any faithful representation ![]() $\rho :G\to GL(N)$ over
$\rho :G\to GL(N)$ over ![]() ${\mathbb {Q}}$, let the ‘
${\mathbb {Q}}$, let the ‘![]() $\rho$-Hecke orbit’ be
$\rho$-Hecke orbit’ be
By Theorem 2.11, we also have
Proposition 2.15 The ![]() $\rho$-Hecke orbit
$\rho$-Hecke orbit ![]() $\mathcal {H}^\rho (x_0)$ is contained in the generalised Hecke orbit
$\mathcal {H}^\rho (x_0)$ is contained in the generalised Hecke orbit ![]() $\mathcal {H}(x_0)$.
$\mathcal {H}(x_0)$.
The ![]() $\rho$-Hecke orbit
$\rho$-Hecke orbit ![]() $\mathcal {H}^\rho (x_0)$ is a finite union of geometric Hecke orbits
$\mathcal {H}^\rho (x_0)$ is a finite union of geometric Hecke orbits ![]() $\mathcal {H}^g(x_0)\cup \cdots \cup \mathcal {H}^\rho (x_k)$.
$\mathcal {H}^g(x_0)\cup \cdots \cup \mathcal {H}^\rho (x_k)$.
The first statement is clear from the definition of ![]() $\mathcal {H}^\rho (x_0)$. The second statement follows from the second definition of
$\mathcal {H}^\rho (x_0)$. The second statement follows from the second definition of ![]() $\mathcal {H}^\rho (x_0)$ and [Reference RichardsonRic67].
$\mathcal {H}^\rho (x_0)$ and [Reference RichardsonRic67].
The number of geometric Hecke orbits is bounded independently from ![]() $\rho$ thanks to Theorem 2.4. It is unclear whether we can achieve
$\rho$ thanks to Theorem 2.4. It is unclear whether we can achieve ![]() $\mathcal {H}^\rho (x_0)=\mathcal {H}(x_0)$ for a sufficiently general representation
$\mathcal {H}^\rho (x_0)=\mathcal {H}(x_0)$ for a sufficiently general representation ![]() $\rho$.
$\rho$.
3. Galois functoriality on the generalised Hecke orbit
In §§ 3.1 and 3.2 we state known definitions and properties for the convenience of the reader. Details can be found, for instance, in [Reference Ullmo and YafaevUY13]. In § 3.3 we relate cardinality of Galois orbits and cardinality of orbits in adelic groups. This is essential to our approach to the estimates of § 1.3.2 through adelic methods.
3.1 Galois representations
Our statements will use the following terminology.
Definition 3.1 (Galois representations)
Let ![]() $(M,X_M)$ be a Shimura datum, let
$(M,X_M)$ be a Shimura datum, let ![]() $x_0$ be a point in
$x_0$ be a point in ![]() $X_M$, and let
$X_M$, and let ![]() $E\leq {\mathbb {C}}$ be a subfield containing the reflex field
$E\leq {\mathbb {C}}$ be a subfield containing the reflex field ![]() $E(M,X_M)$.
$E(M,X_M)$.
We say that a continuous homomorphism
is a Galois representation (defined over ![]() $E$) for
$E$) for ![]() $x_0$ (in
$x_0$ (in ![]() $X_M$) if: for any compact open subgroup
$X_M$) if: for any compact open subgroup ![]() $K'\leq M({\mathbb {A}}_f)$, denoting
$K'\leq M({\mathbb {A}}_f)$, denoting ![]() $[x_0,1]'$ the image of
$[x_0,1]'$ the image of ![]() $(x_0,1)$ in
$(x_0,1)$ in ![]() $Sh_{K'}(M,X_M)$, we have
$Sh_{K'}(M,X_M)$, we have ![]() $[x_0,1]'\in Sh_{K'}(M,X_M)(\overline {E})$ and
$[x_0,1]'\in Sh_{K'}(M,X_M)(\overline {E})$ and
In the important case of moduli spaces of abelian varieties, a representation ![]() $\rho _{x_0}$ can be directly constructed from the linear Galois action on the Tate module (see [Reference Ullmo and YafaevUY13, Reference Cadoret and MoonenCM20]).
$\rho _{x_0}$ can be directly constructed from the linear Galois action on the Tate module (see [Reference Ullmo and YafaevUY13, Reference Cadoret and MoonenCM20]).
Here we only need the existence of a ![]() $\rho _{x_0}$.
$\rho _{x_0}$.
Proposition 3.2 (Existence of Galois representations)
Let ![]() $[x_0,1]\in Sh_{K_M}(M,X_M)(E')$ be a point defined over a field
$[x_0,1]\in Sh_{K_M}(M,X_M)(E')$ be a point defined over a field ![]() $E'\leq {\mathbb {C}}$ in a Shimura variety.
$E'\leq {\mathbb {C}}$ in a Shimura variety.
Then there exist a finite extension ![]() $E/E'$ and a Galois representation defined over
$E/E'$ and a Galois representation defined over ![]() $E$ for
$E$ for ![]() $x_0$ in
$x_0$ in ![]() $X_M$.
$X_M$.
The main ingredient in this proposition is the following, which is part of the definition of canonical models: for any ![]() $[x_0,m_0]$, any
$[x_0,m_0]$, any ![]() $m\in M({\mathbb {A}}_f)$ and
$m\in M({\mathbb {A}}_f)$ and ![]() $\sigma \in Aut({\mathbb {C}}/E(M,X_M))$,
$\sigma \in Aut({\mathbb {C}}/E(M,X_M))$,
The continuity of ![]() $\rho _{x_0}$ is used in the following lemma.
$\rho _{x_0}$ is used in the following lemma.
Lemma 3.3 Let ![]() $K$ be an open subgroup of
$K$ be an open subgroup of ![]() $M({\mathbb {A}}_f)$. Then, after possibly replacing
$M({\mathbb {A}}_f)$. Then, after possibly replacing ![]() $E$ by a finite extension, we have
$E$ by a finite extension, we have
Proof. Such an extension corresponds to the open subgroup ![]() $\stackrel {-1}{\rho _{x_0}}(K)\leq {\rm Gal}(\overline {E}/E)$.
$\stackrel {-1}{\rho _{x_0}}(K)\leq {\rm Gal}(\overline {E}/E)$.
Comments
If ![]() $K$ is sufficiently small so that
$K$ is sufficiently small so that ![]() $K\cap Z_G(M_0)({\mathbb {Q}})=\{1\}$, for instance if
$K\cap Z_G(M_0)({\mathbb {Q}})=\{1\}$, for instance if ![]() $K$ is neat then (see [Reference Klingler and YafaevKY14, § 4.1.4]) for any field
$K$ is neat then (see [Reference Klingler and YafaevKY14, § 4.1.4]) for any field ![]() $E\leq {\mathbb {C}}$, there is at most one Galois representation
$E\leq {\mathbb {C}}$, there is at most one Galois representation ![]() $\rho _{x_0}$ satisfying (12).
$\rho _{x_0}$ satisfying (12).
3.2 Functoriality of the Galois representation
In the next statement we denote by ![]() $E(G,X)$ the reflex field of a Shimura datum
$E(G,X)$ the reflex field of a Shimura datum ![]() $(G,X)$. It is a number field over which
$(G,X)$. It is a number field over which ![]() $Sh(G,X)$ (and, hence, all the
$Sh(G,X)$ (and, hence, all the ![]() $Sh_K(G,X)$) admits a canonical model.
$Sh_K(G,X)$) admits a canonical model.
Proposition 3.4 (Functoriality)
Let ![]() $\phi :(M,X_M)\to (G,X)$ be a morphism of Shimura data, and
$\phi :(M,X_M)\to (G,X)$ be a morphism of Shimura data, and ![]() $x_0$ a point in
$x_0$ a point in ![]() $X_M$.
$X_M$.
If ![]() $\rho _{x_0}$ is a Galois representation defined over a field
$\rho _{x_0}$ is a Galois representation defined over a field ![]() $E$ for
$E$ for ![]() $x_0$, then
$x_0$, then
is a Galois representation defined over ![]() $E\cdot E(G,X)$ for
$E\cdot E(G,X)$ for ![]() $\phi (x_0)$ in
$\phi (x_0)$ in ![]() $X$.
$X$.
This follows from the definition and the identity
which holds when ![]() $\sigma \in \operatorname {Aut}({\mathbb {C}}/E(M,X_M)E(G,X))$. Equivalently, the Shimura morphisms induced by
$\sigma \in \operatorname {Aut}({\mathbb {C}}/E(M,X_M)E(G,X))$. Equivalently, the Shimura morphisms induced by ![]() $\phi$ are defined over
$\phi$ are defined over ![]() $E(M,X_M)E(G,X)$. (See [Reference DeligneDel71, 1.14, 5.1].)
$E(M,X_M)E(G,X)$. (See [Reference DeligneDel71, 1.14, 5.1].)
The compositum field ![]() $E\cdot E(G,X)\leq {\mathbb {C}}$ is a finite extension of
$E\cdot E(G,X)\leq {\mathbb {C}}$ is a finite extension of ![]() $E$ which does not depend on the morphism
$E$ which does not depend on the morphism ![]() $\phi$. With our definition, it also does not depend on the compact open subgroups. As a consequence, Galois representations for points in the same generalised Hecke orbit can be deduced from each other, after passing to the same finite extension
$\phi$. With our definition, it also does not depend on the compact open subgroups. As a consequence, Galois representations for points in the same generalised Hecke orbit can be deduced from each other, after passing to the same finite extension ![]() $E\cdot E(G,X)/E$.
$E\cdot E(G,X)/E$.
For future reference we summarise the above statements as follows.
Proposition 3.5 We keep the same notation. For any ![]() $\sigma \in Gal(\overline {E}/E\cdot E(G,X))$, any
$\sigma \in Gal(\overline {E}/E\cdot E(G,X))$, any ![]() $g\in G({\mathbb {A}}_f)$, and any
$g\in G({\mathbb {A}}_f)$, and any ![]() $\gamma \in G({\mathbb {Q}})$, we have
$\gamma \in G({\mathbb {Q}})$, we have
where
is a Galois representation defined over ![]() $E\cdot E(G,X)$ for
$E\cdot E(G,X)$ for ![]() $\gamma \cdot \phi (x_0)$ in
$\gamma \cdot \phi (x_0)$ in ![]() $X$.
$X$.
3.3 Galois orbits versus Adelic orbits
Let ![]() $U=\rho _{x_0}(Gal(\overline {E}/E))$. By definition, we have
$U=\rho _{x_0}(Gal(\overline {E}/E))$. By definition, we have
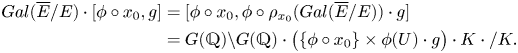 \begin{align*} Gal(\overline{E}/E)\cdot [\phi\circ x_0,g]&= [\phi\circ x_0,\phi\circ\rho_{x_0}(Gal(\overline{E}/E))\cdot g]\\ &= G({\mathbb{Q}})\backslash G({\mathbb{Q}})\cdot \big(\{\phi\circ x_0\}\times \phi(U)\cdot g\big)\cdot K\cdot /K. \end{align*}
\begin{align*} Gal(\overline{E}/E)\cdot [\phi\circ x_0,g]&= [\phi\circ x_0,\phi\circ\rho_{x_0}(Gal(\overline{E}/E))\cdot g]\\ &= G({\mathbb{Q}})\backslash G({\mathbb{Q}})\cdot \big(\{\phi\circ x_0\}\times \phi(U)\cdot g\big)\cdot K\cdot /K. \end{align*}
The next proposition reduces the estimation of the size of the Galois orbit to that of the ![]() $\phi (U)$-orbit
$\phi (U)$-orbit ![]() $\phi (U)\cdot g\cdot K\cdot /K$.
$\phi (U)\cdot g\cdot K\cdot /K$.
Proposition 3.6 There is a real number ![]() $C\in {\mathbb {R}}_{>0}$ such that
$C\in {\mathbb {R}}_{>0}$ such that
After possibly passing to a finite extension of ![]() $E$, we may choose
$E$, we may choose ![]() $C=1$.
$C=1$.
Proof. We want to bound the cardinality of the fibres of the map
We first describe the fibres. Let ![]() $Z_\phi :=Z_G(\phi (M))$. The classical description of Hecke orbits gives an identity
$Z_\phi :=Z_G(\phi (M))$. The classical description of Hecke orbits gives an identity
(This follows from ![]() $G({\mathbb {Q}})\cap Stab_{G({\mathbb {R}})}(\phi \circ x_0)=Z_\phi ({\mathbb {Q}})$ in
$G({\mathbb {Q}})\cap Stab_{G({\mathbb {R}})}(\phi \circ x_0)=Z_\phi ({\mathbb {Q}})$ in ![]() $G({\mathbb {R}})$. We have embedded
$G({\mathbb {R}})$. We have embedded ![]() $Z_{\phi }({\mathbb {Q}})$ in
$Z_{\phi }({\mathbb {Q}})$ in ![]() $G({\mathbb {A}})$ in the first line, and in
$G({\mathbb {A}})$ in the first line, and in ![]() $G({\mathbb {A}}_f)$ in the second line.)
$G({\mathbb {A}}_f)$ in the second line.)
Define
The map (13) can be written as a quotient map
It will suffice to bound the order ![]() $\lvert \Gamma \rvert$.
$\lvert \Gamma \rvert$.
The group ![]() $Z_\phi ({\mathbb {Q}})$ is discrete in
$Z_\phi ({\mathbb {Q}})$ is discrete in ![]() $G({\mathbb {A}}_f)$ because
$G({\mathbb {A}}_f)$ because ![]() $Z_\phi ({\mathbb {R}})$ is compact modulo
$Z_\phi ({\mathbb {R}})$ is compact modulo ![]() $Z(G)({\mathbb {R}})$ and
$Z(G)({\mathbb {R}})$ and ![]() $Z(G)({\mathbb {Q}})$ is discrete in
$Z(G)({\mathbb {Q}})$ is discrete in ![]() $G({\mathbb {A}}_f)$ (see [Reference Ullmo and YafaevUY13, Appendix Lemma 5.13]), where
$G({\mathbb {A}}_f)$ (see [Reference Ullmo and YafaevUY13, Appendix Lemma 5.13]), where ![]() $Z(G)$ is the centre of
$Z(G)$ is the centre of ![]() $G$. As usual, we assume that
$G$. As usual, we assume that ![]() $G$ is the generic Mumford–Tate group on
$G$ is the generic Mumford–Tate group on ![]() $X$. Therefore,
$X$. Therefore, ![]() $\Gamma$ is compact and discrete, and thus is finite.
$\Gamma$ is compact and discrete, and thus is finite.
We will realise ![]() $\Gamma$ as a finite arithmetic group. We choose a faithful representation
$\Gamma$ as a finite arithmetic group. We choose a faithful representation ![]() $G\to GL(N)$ defined over
$G\to GL(N)$ defined over ![]() ${\mathbb {Q}}$, and identify
${\mathbb {Q}}$, and identify ![]() $M$ and
$M$ and ![]() $G$ with their images in
$G$ with their images in ![]() $GL(N)$.
$GL(N)$.
We let ![]() $K[m]=\ker (GL(N,\widehat {{\mathbb {Z}}})\to GL(N,{{\mathbb {Z}}}/(m))$ for
$K[m]=\ker (GL(N,\widehat {{\mathbb {Z}}})\to GL(N,{{\mathbb {Z}}}/(m))$ for ![]() $m\in {\mathbb {Z}}$.
$m\in {\mathbb {Z}}$.
There is a maximal compact subgroup ![]() $K'$ of
$K'$ of ![]() $GL(N,{\mathbb {A}}_f)$ which contains
$GL(N,{\mathbb {A}}_f)$ which contains ![]() $K$. In
$K$. In ![]() $GL(N,{\mathbb {A}}_f)$ all maximal compact subgroups are conjugated:
$GL(N,{\mathbb {A}}_f)$ all maximal compact subgroups are conjugated: ![]() $K'$ is of the form
$K'$ is of the form ![]() $h\cdot GL(N,\widehat {{\mathbb {Z}}})\cdot h^{-1}$ with
$h\cdot GL(N,\widehat {{\mathbb {Z}}})\cdot h^{-1}$ with ![]() $h\in GL(N,{\mathbb {A}}_f)$. We may even choose
$h\in GL(N,{\mathbb {A}}_f)$. We may even choose ![]() $h\in GL(N,{\mathbb {Q}})$ (this is a consequence of the fact that the class number of
$h\in GL(N,{\mathbb {Q}})$ (this is a consequence of the fact that the class number of ![]() $GL(N)/{\mathbb {Q}}$ is one).
$GL(N)/{\mathbb {Q}}$ is one).
Conjugating the representation by ![]() $h^{-1}$ we may assume
$h^{-1}$ we may assume ![]() $h=1$: we have
$h=1$: we have
If ![]() $m=3$ we pass to the finite extension of
$m=3$ we pass to the finite extension of ![]() $E$ corresponding to the subgroup
$E$ corresponding to the subgroup ![]() $\stackrel {-1}{\rho _{x_0}}(U\cap K[m])$ of
$\stackrel {-1}{\rho _{x_0}}(U\cap K[m])$ of ![]() ${\rm Gal}(\overline {E}/E)$. In any case we may assume
${\rm Gal}(\overline {E}/E)$. In any case we may assume
From Proposition 3.5, we know that ![]() $\phi =\gamma \phi _0 \gamma ^{-1}$ for some
$\phi =\gamma \phi _0 \gamma ^{-1}$ for some ![]() $\gamma \in GL(N,{\mathbb {Q}})$. It follows that
$\gamma \in GL(N,{\mathbb {Q}})$. It follows that
and, thus,
Conjugating by ![]() $\gamma ^{-1}$ yields
$\gamma ^{-1}$ yields
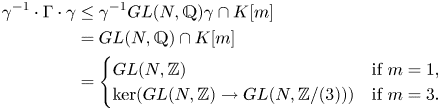 \begin{align*} \gamma^{-1}\cdot \Gamma\cdot \gamma &\leq \gamma^{-1}GL(N,{\mathbb{Q}})\gamma\cap K[m]\\ &=GL(N,{\mathbb{Q}})\cap K[m]\\ &= \begin{cases} GL(N,{\mathbb{Z}}) & \text{if $m=1$,}\\ \ker(GL(N,{\mathbb{Z}})\to GL(N,{\mathbb{Z}}/(3))) & \text{if $m=3$.} \end{cases} \end{align*}
\begin{align*} \gamma^{-1}\cdot \Gamma\cdot \gamma &\leq \gamma^{-1}GL(N,{\mathbb{Q}})\gamma\cap K[m]\\ &=GL(N,{\mathbb{Q}})\cap K[m]\\ &= \begin{cases} GL(N,{\mathbb{Z}}) & \text{if $m=1$,}\\ \ker(GL(N,{\mathbb{Z}})\to GL(N,{\mathbb{Z}}/(3))) & \text{if $m=3$.} \end{cases} \end{align*}
Recall that ![]() $\lvert \Gamma \rvert =\lvert \gamma ^{-1}\Gamma \gamma \rvert$. We may thus conclude by applying the following lemma to
$\lvert \Gamma \rvert =\lvert \gamma ^{-1}\Gamma \gamma \rvert$. We may thus conclude by applying the following lemma to ![]() $\gamma ^{-1}\cdot \Gamma \cdot \gamma$. It follows that for
$\gamma ^{-1}\cdot \Gamma \cdot \gamma$. It follows that for ![]() $m=1$,
$m=1$, ![]() $|\Gamma |$ is bounded independently of
$|\Gamma |$ is bounded independently of ![]() $\phi$ and for
$\phi$ and for ![]() $m=3$,
$m=3$, ![]() $|\Gamma |=1$.
$|\Gamma |=1$.
Lemma 3.7 For every ![]() $N$, there is a real number
$N$, there is a real number ![]() $C(N)$ such that, for every finite subgroup
$C(N)$ such that, for every finite subgroup ![]() $\Gamma \leq GL(N,{\mathbb {Z}})$ we have
$\Gamma \leq GL(N,{\mathbb {Z}})$ we have
and if ![]() $\Gamma \leq \ker (GL(N,{\mathbb {Z}})\to GL(N,{\mathbb {Z}}/(3)))$, then
$\Gamma \leq \ker (GL(N,{\mathbb {Z}})\to GL(N,{\mathbb {Z}}/(3)))$, then ![]() $\Gamma =1$.
$\Gamma =1$.
Proof. From [Reference Platonov and RapinchukPR94, Lemma 4.19.(Minkowski), p. 232] the kernel has no nontrivial torsion. This implies the second assertion.
This also implies that the reduction map ![]() $GL(N,{\mathbb {Z}})\to GL(N,{\mathbb {Z}}/(3))$ is injective on
$GL(N,{\mathbb {Z}})\to GL(N,{\mathbb {Z}}/(3))$ is injective on ![]() $\Gamma$, thus inducing an embedding of
$\Gamma$, thus inducing an embedding of ![]() $\Gamma$ in
$\Gamma$ in ![]() $GL(N,{\mathbb {Z}}/(3))$. The first conclusion follows with
$GL(N,{\mathbb {Z}}/(3))$. The first conclusion follows with
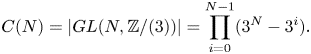 \[ C(N)=\lvert GL(N,{\mathbb{Z}}/(3)) \rvert=\prod_{i=0}^{N-1}(3^N-3^i). \]
\[ C(N)=\lvert GL(N,{\mathbb{Z}}/(3)) \rvert=\prod_{i=0}^{N-1}(3^N-3^i). \]
4. Invariant heights on Hecke orbits
4.1 Height functions
4.1.1 Local affine height functions over  ${\mathbb {R}}$ or
${\mathbb {R}}$ or  ${\mathbb {Q}}_p$
${\mathbb {Q}}_p$
Let ![]() $W$ be an affine variety over
$W$ be an affine variety over ![]() $K={\mathbb {R}}$ or
$K={\mathbb {R}}$ or ![]() $K={\mathbb {Q}}_p$. For every affine embedding defined over
$K={\mathbb {Q}}_p$. For every affine embedding defined over ![]() $K$
$K$
there is an associated affine local Weil height function ![]() $H_{\iota _K}:W(K)\to {\mathbb {R}}_{\geq 0}$ given by
$H_{\iota _K}:W(K)\to {\mathbb {R}}_{\geq 0}$ given by
where ![]() $\lvert - \rvert _K$ is the standard absolute value on
$\lvert - \rvert _K$ is the standard absolute value on ![]() $K$.
$K$.
4.1.2 Affine height functions over  ${\mathbb {Q}}$
${\mathbb {Q}}$
When ![]() $W$ and
$W$ and ![]() $\iota :=\iota _K$ are defined over
$\iota :=\iota _K$ are defined over ![]() ${\mathbb {Q}}$, we can define, for
${\mathbb {Q}}$, we can define, for ![]() $w\in W({\mathbb {Q}})$,
$w\in W({\mathbb {Q}})$,
We define more generally, for ![]() $w=(w_p)_p\in W({\mathbb {A}}_f)$,
$w=(w_p)_p\in W({\mathbb {A}}_f)$,
When ![]() $W$ and the embedding
$W$ and the embedding ![]() $\iota _{{\mathbb {R}}}$, respectively,
$\iota _{{\mathbb {R}}}$, respectively, ![]() $\iota _{{\mathbb {Q}}_p}$, respectively,
$\iota _{{\mathbb {Q}}_p}$, respectively, ![]() $\iota$ are clear from the context, we will simply write
$\iota$ are clear from the context, we will simply write
Then (15) becomes
4.2 Polynomial equivalence and functoriality of heights
We recall the functoriality properties of heights. See [Reference SerreSer97] or [Reference Bombieri and GublerBG06] for corresponding statements about projective Weil heights. See Definition 1.7 for the symbols ![]() $\preccurlyeq$ and
$\preccurlyeq$ and ![]() $\approx$.
$\approx$.
Theorem 4.1 (Functoriality of heights)
Let ![]() $\phi :V\to V'$ be a morphism of affine varieties over
$\phi :V\to V'$ be a morphism of affine varieties over ![]() ${\mathbb {R}}$, respectively,
${\mathbb {R}}$, respectively, ![]() ${\mathbb {Q}}_p$, respectively,
${\mathbb {Q}}_p$, respectively, ![]() ${\mathbb {Q}}$, and let
${\mathbb {Q}}$, and let
be an affine embedding of ![]() $V$, and let
$V$, and let ![]() $\iota '_{{\mathbb {R}}}:V'\to {\mathbb {A}}^{N'}_{\mathbb {R}}$, respectively,
$\iota '_{{\mathbb {R}}}:V'\to {\mathbb {A}}^{N'}_{\mathbb {R}}$, respectively, ![]() $\iota '_{{\mathbb {Q}}_p}:V'\to {\mathbb {A}}^{N'}_{{\mathbb {Q}}_p}$, respectively,
$\iota '_{{\mathbb {Q}}_p}:V'\to {\mathbb {A}}^{N'}_{{\mathbb {Q}}_p}$, respectively, ![]() $\iota ':V'\to {\mathbb {A}}^{N'}_{\mathbb {Q}}$ be an affine embedding of
$\iota ':V'\to {\mathbb {A}}^{N'}_{\mathbb {Q}}$ be an affine embedding of ![]() $V'$.
$V'$.
Then, as functions on ![]() $V({\mathbb {R}})$, respectively,
$V({\mathbb {R}})$, respectively, ![]() $V({\mathbb {Q}}_p)$, respectively,
$V({\mathbb {Q}}_p)$, respectively, ![]() $V({\mathbb {Q}})$ and
$V({\mathbb {Q}})$ and ![]() $V({\mathbb {A}}_f)$,
$V({\mathbb {A}}_f)$,
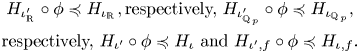 \begin{gather*} H_{\iota'_{\mathbb{R}}}\circ \phi \preccurlyeq H_{\iota_{\mathbb{R}}} , \text{respectively, }H_{\iota'_{{\mathbb{Q}}_p}}\circ \phi \preccurlyeq H_{\iota_{{\mathbb{Q}}_p}},\\ \text{respectively, }H_{\iota'}\circ \phi \preccurlyeq H_{\iota}\text{ and }H_{\iota',f}\circ \phi \preccurlyeq H_{\iota,f}. \end{gather*}
\begin{gather*} H_{\iota'_{\mathbb{R}}}\circ \phi \preccurlyeq H_{\iota_{\mathbb{R}}} , \text{respectively, }H_{\iota'_{{\mathbb{Q}}_p}}\circ \phi \preccurlyeq H_{\iota_{{\mathbb{Q}}_p}},\\ \text{respectively, }H_{\iota'}\circ \phi \preccurlyeq H_{\iota}\text{ and }H_{\iota',f}\circ \phi \preccurlyeq H_{\iota,f}. \end{gather*}
Corollary 4.2 Let ![]() $V$ be an affine algebraic variety over
$V$ be an affine algebraic variety over ![]() ${\mathbb {R}}$, respectively,
${\mathbb {R}}$, respectively, ![]() ${\mathbb {Q}}_p$, respectively,
${\mathbb {Q}}_p$, respectively, ![]() ${\mathbb {Q}}$. Let
${\mathbb {Q}}$. Let
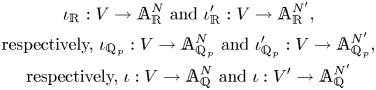 \begin{gather*} \text{$\iota_{{\mathbb{R}}}:V\to {\mathbb{A}}^{N}_{\mathbb{R}}$ and $\iota'_{{\mathbb{R}}}:V\to {\mathbb{A}}^{N'}_{\mathbb{R}}$,}\\ \text{respectively, $\iota_{{\mathbb{Q}}_p}:V\to {\mathbb{A}}^N_{{\mathbb{Q}}_p}$ and $\iota'_{{\mathbb{Q}}_p}:V\to {\mathbb{A}}^{N'}_{{\mathbb{Q}}_p}$,}\\ \text{respectively, $\iota:V\to {\mathbb{A}}^N_{\mathbb{Q}}$ and $\iota:V'\to {\mathbb{A}}^{N'}_{\mathbb{Q}}$} \end{gather*}
\begin{gather*} \text{$\iota_{{\mathbb{R}}}:V\to {\mathbb{A}}^{N}_{\mathbb{R}}$ and $\iota'_{{\mathbb{R}}}:V\to {\mathbb{A}}^{N'}_{\mathbb{R}}$,}\\ \text{respectively, $\iota_{{\mathbb{Q}}_p}:V\to {\mathbb{A}}^N_{{\mathbb{Q}}_p}$ and $\iota'_{{\mathbb{Q}}_p}:V\to {\mathbb{A}}^{N'}_{{\mathbb{Q}}_p}$,}\\ \text{respectively, $\iota:V\to {\mathbb{A}}^N_{\mathbb{Q}}$ and $\iota:V'\to {\mathbb{A}}^{N'}_{\mathbb{Q}}$} \end{gather*}
be affine embeddings of ![]() $V'$.
$V'$.
Then, as functions on ![]() $V({\mathbb {R}})$, respectively,
$V({\mathbb {R}})$, respectively, ![]() $V({\mathbb {Q}}_p)$, respectively,
$V({\mathbb {Q}}_p)$, respectively, ![]() $V({\mathbb {Q}})$ and
$V({\mathbb {Q}})$ and ![]() $V({\mathbb {A}}_f)$,
$V({\mathbb {A}}_f)$,
4.3 Galois invariant height on the Hecke orbit
Let ![]() $S=Sh_K(G,X)$ and
$S=Sh_K(G,X)$ and ![]() $x_0$ be as in § 1.1 and
$x_0$ be as in § 1.1 and ![]() $\rho _{x_0}:{\rm Gal}(\overline {E}/E)\to M({\mathbb {A}}_f)$ be as in (9). Let
$\rho _{x_0}:{\rm Gal}(\overline {E}/E)\to M({\mathbb {A}}_f)$ be as in (9). Let ![]() $W=G\cdot \phi _0\subseteq \mbox {Hom}(M,G)$ be the algebraic variety defined in § 2.1. We have
$W=G\cdot \phi _0\subseteq \mbox {Hom}(M,G)$ be the algebraic variety defined in § 2.1. We have ![]() $W\simeq G/Z_G(M)$. Let
$W\simeq G/Z_G(M)$. Let ![]() $\mbox {Hom}(\mathfrak {m},\mathfrak {g})$ be affine algebraic variety of linear maps
$\mbox {Hom}(\mathfrak {m},\mathfrak {g})$ be affine algebraic variety of linear maps ![]() $\mathfrak {m}\to \mathfrak {g}$. As
$\mathfrak {m}\to \mathfrak {g}$. As ![]() $M$ is connected, we have an embedding
$M$ is connected, we have an embedding
As ![]() $M$ is reductive, the image is closed, by [Reference RichardsonRic67].
$M$ is reductive, the image is closed, by [Reference RichardsonRic67].
We choose a lattice ![]() $\mathfrak {g}_{\mathbb {Z}}\leq \mathfrak {g}$ such that
$\mathfrak {g}_{\mathbb {Z}}\leq \mathfrak {g}$ such that
is stable under the action of ![]() $K\leq G({\mathbb {A}}_f)$. We define
$K\leq G({\mathbb {A}}_f)$. We define ![]() $\mathfrak {m}_{\mathbb {Z}}=\mathfrak {g}_{\mathbb {Z}}\cap \mathfrak {m}$. We choose a basis of
$\mathfrak {m}_{\mathbb {Z}}=\mathfrak {g}_{\mathbb {Z}}\cap \mathfrak {m}$. We choose a basis of ![]() $\mathfrak {g}$ which generates
$\mathfrak {g}$ which generates ![]() $\mathfrak {g}_{\mathbb {Z}}$ and a basis of
$\mathfrak {g}_{\mathbb {Z}}$ and a basis of ![]() $\mathfrak {m}$ which generates
$\mathfrak {m}$ which generates ![]() $\mathfrak {m}_{\mathbb {Z}}$. This choice induces an isomorphism
$\mathfrak {m}_{\mathbb {Z}}$. This choice induces an isomorphism
This induces an affine embedding
by first mapping ![]() $\phi$ to
$\phi$ to ![]() $d\phi$ and then to its matrix with respect to the bases we have chosen.
$d\phi$ and then to its matrix with respect to the bases we have chosen.
We denote by ![]() $H_f:W({\mathbb {A}}_f)\to {\mathbb {Z}}_{\geq 1}$ and
$H_f:W({\mathbb {A}}_f)\to {\mathbb {Z}}_{\geq 1}$ and ![]() $H'_f:\mbox {Hom}(\mathfrak {m}_{{\mathbb {A}}_f},\mathfrak {g}_{{\mathbb {A}}_f})\to {\mathbb {Z}}_{\geq 1}$ the functions given by (17) with respect to the embeddings
$H'_f:\mbox {Hom}(\mathfrak {m}_{{\mathbb {A}}_f},\mathfrak {g}_{{\mathbb {A}}_f})\to {\mathbb {Z}}_{\geq 1}$ the functions given by (17) with respect to the embeddings ![]() $\iota$ and
$\iota$ and ![]() $j$.
$j$.
Proposition 4.3 (Galois invariance)
Let ![]() $\phi _1,\phi _2\in W({\mathbb {Q}})$ be such that
$\phi _1,\phi _2\in W({\mathbb {Q}})$ be such that ![]() $s_1=[\phi _1\circ x_0,g_1]$ and
$s_1=[\phi _1\circ x_0,g_1]$ and ![]() $s_2=[\phi _2\circ x_0,g_2]$ define points in
$s_2=[\phi _2\circ x_0,g_2]$ define points in ![]() $\mathcal {H}^g(s_0)$, where
$\mathcal {H}^g(s_0)$, where ![]() $g_1,g_2\in G({\mathbb {A}}_f)$, and assume that there exists a
$g_1,g_2\in G({\mathbb {A}}_f)$, and assume that there exists a ![]() $\sigma \in {\rm Gal}(\overline {E}/E)$ such that
$\sigma \in {\rm Gal}(\overline {E}/E)$ such that
Then
We first remark, from the formula
that for every ![]() $\widehat {{\mathbb {Z}}}$-module automorphism
$\widehat {{\mathbb {Z}}}$-module automorphism ![]() $u:\mathfrak {m}_{\widehat {{\mathbb {Z}}}}\to \mathfrak {m}_{\widehat {{\mathbb {Z}}}}$ and
$u:\mathfrak {m}_{\widehat {{\mathbb {Z}}}}\to \mathfrak {m}_{\widehat {{\mathbb {Z}}}}$ and ![]() $k:\mathfrak {g}_{\widehat {{\mathbb {Z}}}}\to \mathfrak {g}_{\widehat {{\mathbb {Z}}}}$, we have
$k:\mathfrak {g}_{\widehat {{\mathbb {Z}}}}\to \mathfrak {g}_{\widehat {{\mathbb {Z}}}}$, we have
When ![]() $\psi =d\phi$, and
$\psi =d\phi$, and ![]() $k=ad_{k'}:\mathfrak {g}\to \mathfrak {g}$ with
$k=ad_{k'}:\mathfrak {g}\to \mathfrak {g}$ with ![]() $k'\in K$ and
$k'\in K$ and ![]() $u=ad_{u'}:\mathfrak {m}\to \mathfrak {m}$ with
$u=ad_{u'}:\mathfrak {m}\to \mathfrak {m}$ with ![]() $u'\in K\cap M({\mathbb {A}}_f)$, this gives, with
$u'\in K\cap M({\mathbb {A}}_f)$, this gives, with ![]() $AD_{k'}\circ \phi \circ AD_{u'}:m\mapsto k'\phi (u'mu'^{-1})k'^{-1}$,
$AD_{k'}\circ \phi \circ AD_{u'}:m\mapsto k'\phi (u'mu'^{-1})k'^{-1}$,
Proof of Proposition 4.3 We define ![]() $u=\rho _{x_0}(\sigma )\in M({\mathbb {A}}_f)\cap K$. From (20) and the functoriality of Galois action Propositions 3.4 and 3.5, we have
$u=\rho _{x_0}(\sigma )\in M({\mathbb {A}}_f)\cap K$. From (20) and the functoriality of Galois action Propositions 3.4 and 3.5, we have
Hence, there exists ![]() $\gamma \in G({\mathbb {Q}})$ and
$\gamma \in G({\mathbb {Q}})$ and ![]() $k\in K$ such that
$k\in K$ such that
By Lemma 2.5, we also have ![]() $\gamma \cdot \phi _1\cdot \gamma ^{-1}=\phi _2$. Thus,
$\gamma \cdot \phi _1\cdot \gamma ^{-1}=\phi _2$. Thus,
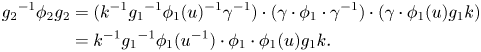 \begin{align*} {g_2}^{-1}\phi_2 g_2&= (k^{-1}{g_1}^{-1}\phi_1(u)^{-1}\gamma^{-1}) \cdot (\gamma\cdot \phi_1\cdot \gamma^{-1}) \cdot (\gamma\cdot \phi_1(u)g_1 k)\\ &= k^{-1}{g_1}^{-1}\phi_1(u^{-1})\cdot \phi_1 \cdot \phi_1(u)g_1 k. \end{align*}
\begin{align*} {g_2}^{-1}\phi_2 g_2&= (k^{-1}{g_1}^{-1}\phi_1(u)^{-1}\gamma^{-1}) \cdot (\gamma\cdot \phi_1\cdot \gamma^{-1}) \cdot (\gamma\cdot \phi_1(u)g_1 k)\\ &= k^{-1}{g_1}^{-1}\phi_1(u^{-1})\cdot \phi_1 \cdot \phi_1(u)g_1 k. \end{align*}
We have
and, hence,
We finally have, using (23),
4.3.1 Height function on the generalised Hecke orbit  $\mathcal {H}([x_0,1])$
$\mathcal {H}([x_0,1])$
The function ![]() $H'_f$ on
$H'_f$ on ![]() $\mbox {Hom}(\mathfrak {m}_{{\mathbb {A}}_f},\mathfrak {g}_{{\mathbb {A}}_f})$ induces, at the level of the
$\mbox {Hom}(\mathfrak {m}_{{\mathbb {A}}_f},\mathfrak {g}_{{\mathbb {A}}_f})$ induces, at the level of the ![]() $Sh_K(G,X)$, a function
$Sh_K(G,X)$, a function ![]() $H_{s_0}$ on the generalised Hecke orbit
$H_{s_0}$ on the generalised Hecke orbit ![]() $\mathcal {H}(s_0)$ of
$\mathcal {H}(s_0)$ of ![]() $s_0:=[x_0,1]$, given as follows. For
$s_0:=[x_0,1]$, given as follows. For ![]() $\phi \in \mbox {Hom}(\mathfrak {m}_{\mathbb {Q}},\mathfrak {g}_{\mathbb {Q}})$ such that
$\phi \in \mbox {Hom}(\mathfrak {m}_{\mathbb {Q}},\mathfrak {g}_{\mathbb {Q}})$ such that ![]() $\phi \circ x_0\in X$ and
$\phi \circ x_0\in X$ and ![]() $g\in G({\mathbb {A}}_f)$, we define
$g\in G({\mathbb {A}}_f)$, we define
The function ![]() $H_{s_0}$ depends on the choices we have made, but different choices will produce the same function, up to a bounded factor.
$H_{s_0}$ depends on the choices we have made, but different choices will produce the same function, up to a bounded factor.
The case ![]() $\sigma =1$ of Proposition 4.3 implies that
$\sigma =1$ of Proposition 4.3 implies that ![]() $H_{s_0}$ is well defined. Proposition 4.3 can then be rephrased as follows.
$H_{s_0}$ is well defined. Proposition 4.3 can then be rephrased as follows.
Lemma 4.4 For every ![]() $\sigma \in {\rm Gal}(\overline {E}/E)$ and
$\sigma \in {\rm Gal}(\overline {E}/E)$ and ![]() $s\in \mathcal {H}(s_0)$ we have
$s\in \mathcal {H}(s_0)$ we have
5. Height comparison on Siegel sets
The main result of this section, Theorem 5.16, compares, for rational points of ![]() $W=G/Z_G(M)$ contained in a given Siegel set (as in Definition 5.11), the global height
$W=G/Z_G(M)$ contained in a given Siegel set (as in Definition 5.11), the global height ![]() $H_W$ of (4.1.2), with its factor
$H_W$ of (4.1.2), with its factor ![]() $H_{f}$ in (19) (coming from the finite places). The height
$H_{f}$ in (19) (coming from the finite places). The height ![]() $H_W$ is that appearing in our variant (Theorem 7.1) of the theorem of Pila–Wilkie, and
$H_W$ is that appearing in our variant (Theorem 7.1) of the theorem of Pila–Wilkie, and ![]() $H_{f}$ is the height appearing in our Galois bounds (see Theorem 6.4).
$H_{f}$ is the height appearing in our Galois bounds (see Theorem 6.4).
Our Theorem 5.16 extends a result of Orr, in [Reference OrrOrr18], which is only applicable to elements in ![]() $G({\mathbb {Q}})$. We work with elements of
$G({\mathbb {Q}})$. We work with elements of ![]() $W({\mathbb {Q}})$ instead. This is crucial to us as, in our strategy § 1.4, we are working with geometric Hecke orbits.Footnote 10
$W({\mathbb {Q}})$ instead. This is crucial to us as, in our strategy § 1.4, we are working with geometric Hecke orbits.Footnote 10
This section develops different arguments than those of [Reference OrrOrr18]. They are more flexible, which allows us to obtain a more general result.
5.1 Polynomial equivalence and archimedean height
We use Definition 1.7.
Lemma 5.1 Let ![]() $A\subset {\mathbb {R}}^n$ be a semialgebraic subset, and let
$A\subset {\mathbb {R}}^n$ be a semialgebraic subset, and let ![]() $f,g \colon A \longrightarrow {\mathbb {R}}_{\geq 0}$ be semialgebraic and continuous functions. Assume that
$f,g \colon A \longrightarrow {\mathbb {R}}_{\geq 0}$ be semialgebraic and continuous functions. Assume that ![]() $f$ is a proper map.
$f$ is a proper map.
Then
Proof. We claim that the following function
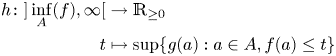 \begin{align*} h \colon ]\inf_A(f), \infty[ &\to {\mathbb{R}}_{\geq 0}\\ t &\mapsto \sup \{g(a): a\in A, f(a) \leq t\} \end{align*}
\begin{align*} h \colon ]\inf_A(f), \infty[ &\to {\mathbb{R}}_{\geq 0}\\ t &\mapsto \sup \{g(a): a\in A, f(a) \leq t\} \end{align*}
is well defined. Fix an arbitrary ![]() $t$ be in
$t$ be in ![]() $]\inf _A(f), \infty [$. The set
$]\inf _A(f), \infty [$. The set ![]() $\{ a\in A: f(a) \leq t\}$ is compact since
$\{ a\in A: f(a) \leq t\}$ is compact since ![]() $f$ is proper. It is nonempty since
$f$ is proper. It is nonempty since ![]() $t> \inf _A(f)$. As
$t> \inf _A(f)$. As ![]() $g$ is continuous,
$g$ is continuous, ![]() $\{g(a): a\in A, f(a) \leq t\}$ is compact and nonempty, and its maximum belongs to
$\{g(a): a\in A, f(a) \leq t\}$ is compact and nonempty, and its maximum belongs to ![]() ${\mathbb {R}}_{\geq 0}$, which proves the claim.
${\mathbb {R}}_{\geq 0}$, which proves the claim.
The function ![]() $h$ is also semialgebraic (see [Reference Bochnak, Coste and RoyBCR98, Proposition 2.2.4.]). By [Reference van den DriesvdDri98, § 4.1 ‘Notes and comments’ and references therein],
$h$ is also semialgebraic (see [Reference Bochnak, Coste and RoyBCR98, Proposition 2.2.4.]). By [Reference van den DriesvdDri98, § 4.1 ‘Notes and comments’ and references therein], ![]() $h$ is polynomially bounded. The conclusion follows.
$h$ is polynomially bounded. The conclusion follows.
The following uses Lemma 5.1 for ![]() $f$ and
$f$ and ![]() $g$, and again after swapping
$g$, and again after swapping ![]() $f$ and
$f$ and ![]() $g$.
$g$.
Corollary 5.2 On a semialgebraic subset ![]() $A\subset {\mathbb {R}}^n$, two proper semialgebraic continuous functions
$A\subset {\mathbb {R}}^n$, two proper semialgebraic continuous functions ![]() $f,g:A\to {\mathbb {R}}$ are polynomially equivalent.
$f,g:A\to {\mathbb {R}}$ are polynomially equivalent.
We will also encounter the following situation.
Lemma 5.3 Let ![]() $A\subset {\mathbb {R}}^n$ and
$A\subset {\mathbb {R}}^n$ and ![]() $B\subset {\mathbb {R}}^m$ be semialgebraic subsets, and
$B\subset {\mathbb {R}}^m$ be semialgebraic subsets, and ![]() $f\colon A \to {\mathbb {R}}_{\geq 0}$ and
$f\colon A \to {\mathbb {R}}_{\geq 0}$ and ![]() $g \colon B \to {\mathbb {R}}_{\geq 0}$ be two proper semialgebraic continuous functions, and
$g \colon B \to {\mathbb {R}}_{\geq 0}$ be two proper semialgebraic continuous functions, and ![]() $p \colon A \to B$ be a proper and continuous semialgebraic function. Then
$p \colon A \to B$ be a proper and continuous semialgebraic function. Then ![]() $g \circ p \approx f$.
$g \circ p \approx f$.
Proof. We note that ![]() $g\circ p$ is proper and continuous because
$g\circ p$ is proper and continuous because ![]() $g$ and
$g$ and ![]() $p$ are. We can apply the Corollary 5.2 to
$p$ are. We can apply the Corollary 5.2 to ![]() $f$ and
$f$ and ![]() $g\circ p$.
$g\circ p$.
Lemma 5.4 Let ![]() $V$ be an affine algebraic variety over
$V$ be an affine algebraic variety over ![]() ${\mathbb {R}}$. Let
${\mathbb {R}}$. Let ![]() $\phi :V\to {\mathbb {A}}^N$, and
$\phi :V\to {\mathbb {A}}^N$, and ![]() $\phi ':V\to {\mathbb {A}}^M$ be two closed embeddings, and let
$\phi ':V\to {\mathbb {A}}^M$ be two closed embeddings, and let ![]() $H_\phi$ and
$H_\phi$ and ![]() $H_{\phi '}$ be defined as in (14).
$H_{\phi '}$ be defined as in (14).
Then ![]() $H_\phi$ and
$H_\phi$ and ![]() $H_{\phi '}$ are semialgebraic continuous proper functions, and
$H_{\phi '}$ are semialgebraic continuous proper functions, and
Proof. The real algebraic map ![]() $V({\mathbb {R}})\to {\mathbb {R}}^N$ induced by the Zariski-closed embedding
$V({\mathbb {R}})\to {\mathbb {R}}^N$ induced by the Zariski-closed embedding ![]() $\phi$ is a closed embedding for the real topology. The functions
$\phi$ is a closed embedding for the real topology. The functions ![]() $\lVert ~ \rVert _{\infty }:{\mathbb {R}}^N\to {\mathbb {R}}_{\geq 0}$ and
$\lVert ~ \rVert _{\infty }:{\mathbb {R}}^N\to {\mathbb {R}}_{\geq 0}$ and ![]() $t\mapsto \max \{1;t\}:{\mathbb {R}}_{\geq 0}\xrightarrow {} {\mathbb {R}}_{\geq 0}$ are semialgebraic continuous proper maps. The composite map
$t\mapsto \max \{1;t\}:{\mathbb {R}}_{\geq 0}\xrightarrow {} {\mathbb {R}}_{\geq 0}$ are semialgebraic continuous proper maps. The composite map ![]() $H_\phi$, and likewise
$H_\phi$, and likewise ![]() $H_{\phi '}$, are thus semialgebraic continuous and proper on
$H_{\phi '}$, are thus semialgebraic continuous and proper on ![]() $V({\mathbb {R}})$. We conclude with Corollary 5.2.
$V({\mathbb {R}})$. We conclude with Corollary 5.2.
Lemma 5.5 Let ![]() $p:U\to V$ be a morphism of affine algebraic varieties over
$p:U\to V$ be a morphism of affine algebraic varieties over ![]() ${\mathbb {R}}$, and
${\mathbb {R}}$, and ![]() $\phi _U:U\to {\mathbb {A}}_{\mathbb {R}}^N$ and
$\phi _U:U\to {\mathbb {A}}_{\mathbb {R}}^N$ and ![]() $\phi _V:V\to {\mathbb {A}}^M_{\mathbb {R}}$ be closed embeddings. Let
$\phi _V:V\to {\mathbb {A}}^M_{\mathbb {R}}$ be closed embeddings. Let ![]() $H_{\phi _U}$ and
$H_{\phi _U}$ and ![]() $H_{\phi _V}$ be defined as in (14).
$H_{\phi _V}$ be defined as in (14).
Let ![]() $A\subset U({\mathbb {R}})$ be a semialgebraic subset such that
$A\subset U({\mathbb {R}})$ be a semialgebraic subset such that ![]() $p|_A:A\to V({\mathbb {R}})$ is proper. Then, as functions
$p|_A:A\to V({\mathbb {R}})$ is proper. Then, as functions ![]() $A\to {\mathbb {R}}_{\geq 0}$,
$A\to {\mathbb {R}}_{\geq 0}$,
Proof. We know that ![]() $H_{\phi _U}$ and
$H_{\phi _U}$ and ![]() $H_{\phi _V}$ are proper continuous and semialgebraic. As
$H_{\phi _V}$ are proper continuous and semialgebraic. As ![]() $p|_A$ is proper,
$p|_A$ is proper, ![]() $\iota :A\hookrightarrow U({\mathbb {R}})$ is closed. It follows that
$\iota :A\hookrightarrow U({\mathbb {R}})$ is closed. It follows that ![]() $H_{\phi _U}|_A=H_{\phi _U}\circ \iota$ is continuous, proper and semialgebraic. We apply Lemma 5.3 with
$H_{\phi _U}|_A=H_{\phi _U}\circ \iota$ is continuous, proper and semialgebraic. We apply Lemma 5.3 with ![]() $A=U({\mathbb {R}})$,
$A=U({\mathbb {R}})$, ![]() $B=V({\mathbb {R}})$, and
$B=V({\mathbb {R}})$, and ![]() $p|_A$ as
$p|_A$ as ![]() $p$, and
$p$, and ![]() $f=H_{\phi _U}|_A$ and
$f=H_{\phi _U}|_A$ and ![]() $g=H_{\phi _V}$.
$g=H_{\phi _V}$.
5.2 Comparison of archimedean and finite height
Lemma 5.6 Let ![]() $\iota :V\to {\mathbb {A}}^M$ be a closed embedding with
$\iota :V\to {\mathbb {A}}^M$ be a closed embedding with ![]() $V = {{\mathbb {G}}_m}^N$. Then
$V = {{\mathbb {G}}_m}^N$. Then ![]() $H_{\iota,{\mathbb {R}}} \preccurlyeq H_{\iota,f}\text { on }{\mathbb {Q}}^{\times N},$ where
$H_{\iota,{\mathbb {R}}} \preccurlyeq H_{\iota,f}\text { on }{\mathbb {Q}}^{\times N},$ where ![]() $H_{{\mathbb {R}}}$ and
$H_{{\mathbb {R}}}$ and ![]() $H_{f}$ are as in § 4.1.2 (see (18)).
$H_{f}$ are as in § 4.1.2 (see (18)).
Proof. Thanks to Corollary 4.2, we may substitute ![]() $\iota$ with the closed embedding
$\iota$ with the closed embedding
We start with the case ![]() $N=1$. We write an element
$N=1$. We write an element ![]() $t\in {\mathbb {Q}}^\times$ as a reduced fraction
$t\in {\mathbb {Q}}^\times$ as a reduced fraction ![]() $n/m$. We can compute
$n/m$. We can compute
It follows ![]() $H_{\iota _1\otimes {\mathbb {R}}}(t)\leq H_{\iota _1,f}(t)$.
$H_{\iota _1\otimes {\mathbb {R}}}(t)\leq H_{\iota _1,f}(t)$.
For general ![]() $\vec {t}=(t_1,\ldots,t_N)\in {{\mathbb {Q}}^\times }^N$ there is some
$\vec {t}=(t_1,\ldots,t_N)\in {{\mathbb {Q}}^\times }^N$ there is some ![]() $1\leq i\leq N$ such that
$1\leq i\leq N$ such that
By the previous computation we have
We conclude by observing that
as can be seen prime by prime.
Lemma 5.7 For ![]() $V = {\mathbb {G}}_m^N\subset W={\mathbb {A}}^N$, and affine embeddings
$V = {\mathbb {G}}_m^N\subset W={\mathbb {A}}^N$, and affine embeddings ![]() $\iota _V:V\to {\mathbb {A}}^M$, respectively,
$\iota _V:V\to {\mathbb {A}}^M$, respectively, ![]() $\iota _W:W\to {\mathbb {A}}^{M'}$, we have
$\iota _W:W\to {\mathbb {A}}^{M'}$, we have ![]() $H_{\iota _V,f} \preccurlyeq H_{\iota _W}\text { on }{{\mathbb {Q}}^\times }^N$.
$H_{\iota _V,f} \preccurlyeq H_{\iota _W}\text { on }{{\mathbb {Q}}^\times }^N$.
Proof. By Corollary 4.2, we may assume that ![]() $\iota _V$ is
$\iota _V$ is ![]() $\iota _N$ of (25), and that
$\iota _N$ of (25), and that ![]() $\iota _W$ is the identity map. We can again reduce the problem to the case
$\iota _W$ is the identity map. We can again reduce the problem to the case ![]() $N=1$. We write
$N=1$. We write ![]() $t_i=n/m$ as an irreducible fraction and then we have
$t_i=n/m$ as an irreducible fraction and then we have
Corollary 5.8 Let ![]() $C\in {\mathbb {R}}_{>0}$. We have
$C\in {\mathbb {R}}_{>0}$. We have
Proof. In Lemma 5.7, we decompose ![]() $H_{\iota _W}= H_{\iota _W\otimes {\mathbb {R}}}\cdot H_{\iota _W,f}$. By hypothesis,
$H_{\iota _W}= H_{\iota _W\otimes {\mathbb {R}}}\cdot H_{\iota _W,f}$. By hypothesis, ![]() $H_{\iota _W\otimes {\mathbb {R}}}\leq C$, hence
$H_{\iota _W\otimes {\mathbb {R}}}\leq C$, hence ![]() $H_{\iota _W} \preccurlyeq H_{\iota _W,f}\text { on }({\mathbb {Q}}^\times \cap [-C;C])^N$ which allows us to conclude.
$H_{\iota _W} \preccurlyeq H_{\iota _W,f}\text { on }({\mathbb {Q}}^\times \cap [-C;C])^N$ which allows us to conclude.
We establish the following.
Proposition 5.9 Let ![]() $W$ be an affine variety over
$W$ be an affine variety over ![]() ${\mathbb {Q}}$ and let
${\mathbb {Q}}$ and let ![]() $p\colon W \longrightarrow {\mathbb {A}}^r$ be an algebraic map and
$p\colon W \longrightarrow {\mathbb {A}}^r$ be an algebraic map and ![]() $\mathfrak {S} \subset W({\mathbb {R}})$ be a semialgebraic closed subset such that:
$\mathfrak {S} \subset W({\mathbb {R}})$ be a semialgebraic closed subset such that:
(i) we have
 $p(\mathfrak {S}) \subseteq ({\mathbb {R}}^\times )^r$;
$p(\mathfrak {S}) \subseteq ({\mathbb {R}}^\times )^r$;(ii) the restriction
 $p |_{\mathfrak {S}} \colon \mathfrak {S} \longrightarrow {{\mathbb {R}}^\times }^r$ is a proper map;
$p |_{\mathfrak {S}} \colon \mathfrak {S} \longrightarrow {{\mathbb {R}}^\times }^r$ is a proper map;(iii) the image
 $p(\mathfrak {S})$ is bounded in
$p(\mathfrak {S})$ is bounded in  ${\mathbb {R}}^r$.
${\mathbb {R}}^r$.
We fix an affine embedding ![]() $\iota$ of
$\iota$ of ![]() $W$ and use notation (18). Then
$W$ and use notation (18). Then
In particular,
Proof. We denote by ![]() ${{\mathbb {G}}_m}^r\subset {\mathbb {A}}^r$ the affine open subset on which every coordinate is invertible.
${{\mathbb {G}}_m}^r\subset {\mathbb {A}}^r$ the affine open subset on which every coordinate is invertible.
We fix affine embeddings ![]() $\iota _W$ of
$\iota _W$ of ![]() $W$, and
$W$, and ![]() $\iota _{{{\mathbb {G}}_m}^r}$ of
$\iota _{{{\mathbb {G}}_m}^r}$ of ![]() ${{\mathbb {G}}_m}^r$ and
${{\mathbb {G}}_m}^r$ and ![]() $\iota _{{\mathbb {A}}^r}$ of
$\iota _{{\mathbb {A}}^r}$ of ![]() ${\mathbb {A}}^r$.
${\mathbb {A}}^r$.
Because ![]() $p|_{\mathfrak {S}}$ is continuous real algebraic, and (as a function to
$p|_{\mathfrak {S}}$ is continuous real algebraic, and (as a function to ![]() ${\mathbb {R}}^r$) is proper, by Lemma 5.5 we have
${\mathbb {R}}^r$) is proper, by Lemma 5.5 we have
By functoriality of heights, Theorem 4.1, we have, on ![]() $W({\mathbb {Q}})$,
$W({\mathbb {Q}})$,
As ![]() $p(\mathfrak {S})$ is bounded in
$p(\mathfrak {S})$ is bounded in ![]() ${\mathbb {R}}^r$, we have, by Lemma 5.6,
${\mathbb {R}}^r$, we have, by Lemma 5.6,
By hypothesis (iii) we can use Corollary 5.8 and get
Combining these we get, using (26), (28), (29), and then (27),
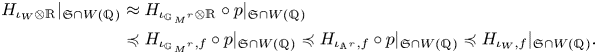 \begin{align*} H_{\iota_W\otimes{\mathbb{R}}}|_{\mathfrak{S}\cap W({\mathbb{Q}})} &\approx H_{\iota_{{{\mathbb{G}}_M}^r}\otimes{\mathbb{R}}}\circ p|_{\mathfrak{S}\cap W({\mathbb{Q}})}\\ & \preccurlyeq H_{\iota_{{{\mathbb{G}}_M}^r},f}\circ p|_{\mathfrak{S}\cap W({\mathbb{Q}})} \preccurlyeq H_{\iota_{{\mathbb{A}}^r},f}\circ p|_{\mathfrak{S}\cap W({\mathbb{Q}})} \preccurlyeq H_{\iota_W,f}|_{\mathfrak{S}\cap W({\mathbb{Q}})}. \end{align*}
\begin{align*} H_{\iota_W\otimes{\mathbb{R}}}|_{\mathfrak{S}\cap W({\mathbb{Q}})} &\approx H_{\iota_{{{\mathbb{G}}_M}^r}\otimes{\mathbb{R}}}\circ p|_{\mathfrak{S}\cap W({\mathbb{Q}})}\\ & \preccurlyeq H_{\iota_{{{\mathbb{G}}_M}^r},f}\circ p|_{\mathfrak{S}\cap W({\mathbb{Q}})} \preccurlyeq H_{\iota_{{\mathbb{A}}^r},f}\circ p|_{\mathfrak{S}\cap W({\mathbb{Q}})} \preccurlyeq H_{\iota_W,f}|_{\mathfrak{S}\cap W({\mathbb{Q}})}. \end{align*}
5.3 Construction of Siegel sets
We start by recalling some facts about parabolic subgroups and Siegel sets. A general reference is [Reference Borel and JiBJ06].
Let ![]() $G_{\mathbb {Q}}$ be a semisimple
$G_{\mathbb {Q}}$ be a semisimple ![]() ${\mathbb {Q}}$-algebraic group of adjoint type. We fix a minimal
${\mathbb {Q}}$-algebraic group of adjoint type. We fix a minimal ![]() ${\mathbb {Q}}$-defined parabolicFootnote 11 subgroup
${\mathbb {Q}}$-defined parabolicFootnote 11 subgroup ![]() $P_{\mathbb {Q}}$. Let
$P_{\mathbb {Q}}$. Let ![]() $G_{\mathbb {R}}$ and
$G_{\mathbb {R}}$ and ![]() $P_{\mathbb {R}}$ be the corresponding
$P_{\mathbb {R}}$ be the corresponding ![]() ${\mathbb {R}}$-algebraic groups.
${\mathbb {R}}$-algebraic groups.
Let ![]() $X$ be the associated symmetric space,Footnote 12 and choose
$X$ be the associated symmetric space,Footnote 12 and choose ![]() $x \in X$ and let
$x \in X$ and let ![]() $\Theta :G_{{\mathbb {R}}}\to G_{{\mathbb {R}}}$ be the Cartan involution associated with
$\Theta :G_{{\mathbb {R}}}\to G_{{\mathbb {R}}}$ be the Cartan involution associated with ![]() $x$. The orbit map
$x$. The orbit map ![]() $g\mapsto g\cdot x$ induces the identification
$g\mapsto g\cdot x$ induces the identification ![]() $G({\mathbb {R}})/K\simeq X$ where
$G({\mathbb {R}})/K\simeq X$ where ![]() $K$ is the maximal compact subgroup
$K$ is the maximal compact subgroup ![]() $\{g\in G({\mathbb {R}}): g=\Theta (g)\}$. We denote by
$\{g\in G({\mathbb {R}}): g=\Theta (g)\}$. We denote by ![]() $K_\infty =K^+$ the neutral component.
$K_\infty =K^+$ the neutral component.
We let ![]() $N_{\mathbb {Q}}$ be the unipotent radical of
$N_{\mathbb {Q}}$ be the unipotent radical of ![]() $P_{\mathbb {Q}}$: thus
$P_{\mathbb {Q}}$: thus ![]() $P_{\mathbb {Q}}/N_{\mathbb {Q}}$ is the maximal reductive quotient of
$P_{\mathbb {Q}}/N_{\mathbb {Q}}$ is the maximal reductive quotient of ![]() $P_{\mathbb {Q}}$. The
$P_{\mathbb {Q}}$. The ![]() ${\mathbb {R}}$-algebraic group
${\mathbb {R}}$-algebraic group
is a maximal ![]() ${\mathbb {R}}$-algebraic reductive subgroup of
${\mathbb {R}}$-algebraic reductive subgroup of ![]() $P_{{\mathbb {R}}}$ (cf. [Reference Borel and JiBJ06, § III.1.9]), not necessarily defined over
$P_{{\mathbb {R}}}$ (cf. [Reference Borel and JiBJ06, § III.1.9]), not necessarily defined over ![]() ${\mathbb {Q}}$, and the map
${\mathbb {Q}}$, and the map ![]() $L\to P_{\mathbb {R}}\to (P_{\mathbb {Q}}/N_{\mathbb {Q}})_{\mathbb {R}}$ is an isomorphism. We denote by
$L\to P_{\mathbb {R}}\to (P_{\mathbb {Q}}/N_{\mathbb {Q}})_{\mathbb {R}}$ is an isomorphism. We denote by ![]() $A'_{\mathbb {Q}}$ the maximal central
$A'_{\mathbb {Q}}$ the maximal central ![]() ${\mathbb {Q}}$-split torus of
${\mathbb {Q}}$-split torus of ![]() $P_{\mathbb {Q}}/N_{\mathbb {Q}}$, and define
$P_{\mathbb {Q}}/N_{\mathbb {Q}}$, and define ![]() $A\leq L$ as the inverse image of
$A\leq L$ as the inverse image of ![]() $A_{\mathbb {R}}$ in
$A_{\mathbb {R}}$ in ![]() $L$. We denote by
$L$. We denote by ![]() $A^+=A({\mathbb {R}})^+$ the neutral component as a real Lie group.
$A^+=A({\mathbb {R}})^+$ the neutral component as a real Lie group.
We denote by ![]() $\Phi$ the set of non-zero weights of the adjoint action of
$\Phi$ the set of non-zero weights of the adjoint action of ![]() $A$ on
$A$ on ![]() $\mathfrak {g}\otimes {\mathbb {R}}$ (the ‘(relative) roots’), and
$\mathfrak {g}\otimes {\mathbb {R}}$ (the ‘(relative) roots’), and ![]() $\Phi ^+$ the subset of weights of the action on
$\Phi ^+$ the subset of weights of the action on ![]() $\mathfrak {n}\otimes {\mathbb {R}}$ (the ‘positive’ ones). The eigenspaces are not necessarily defined over
$\mathfrak {n}\otimes {\mathbb {R}}$ (the ‘positive’ ones). The eigenspaces are not necessarily defined over ![]() ${\mathbb {Q}}$. There exists a unique subset
${\mathbb {Q}}$. There exists a unique subset ![]() $\Delta =\{\alpha _1;\ldots ;\alpha _r\}\subset \Phi ^+$ such that
$\Delta =\{\alpha _1;\ldots ;\alpha _r\}\subset \Phi ^+$ such that ![]() $\alpha _1,\ldots,\alpha _r$ is a basis of
$\alpha _1,\ldots,\alpha _r$ is a basis of ![]() $X(A)=\mbox {Hom}(A,{{\mathbb {G}}_m}_{\mathbb {R}})$ and
$X(A)=\mbox {Hom}(A,{{\mathbb {G}}_m}_{\mathbb {R}})$ and ![]() $\Phi ^+\subset \alpha _1\cdot {\mathbb {Z}}_{\geq 0} + \cdots +\alpha _r\cdot {\mathbb {Z}}_{\geq 0}$. The
$\Phi ^+\subset \alpha _1\cdot {\mathbb {Z}}_{\geq 0} + \cdots +\alpha _r\cdot {\mathbb {Z}}_{\geq 0}$. The ![]() $\alpha _i$ are known as the (relative) simple roots, and
$\alpha _i$ are known as the (relative) simple roots, and ![]() $r$ is equal to the
$r$ is equal to the ![]() ${\mathbb {Q}}$-rank of
${\mathbb {Q}}$-rank of ![]() $G_{\mathbb {Q}}$.
$G_{\mathbb {Q}}$.
The positive Weyl chamber in ![]() $A^+$ is
$A^+$ is
We define
We note that, for every one-dimensional representation ![]() ${\mathbb {Q}}\cdot \eta$ of
${\mathbb {Q}}\cdot \eta$ of ![]() $H_P$, we have
$H_P$, we have
We first define Siegel sets in ![]() $G_{\mathbb {Q}}({\mathbb {R}})$.
$G_{\mathbb {Q}}({\mathbb {R}})$.
Definition 5.10 (Siegel set)
A ![]() ${\mathbb {Q}}$-Siegel set
${\mathbb {Q}}$-Siegel set ![]() $\mathfrak {S}$ in
$\mathfrak {S}$ in ![]() $G_{\mathbb {Q}}({\mathbb {R}})$ with respect to
$G_{\mathbb {Q}}({\mathbb {R}})$ with respect to ![]() $P_{\mathbb {Q}}$ and
$P_{\mathbb {Q}}$ and ![]() $x$ is a subset
$x$ is a subset ![]() $\mathfrak {S}\subseteq G({\mathbb {R}})$ of the following form.
$\mathfrak {S}\subseteq G({\mathbb {R}})$ of the following form.
There is a nonempty open and relatively compact subset ![]() $\Omega \subseteq P_{\mathbb {Q}}({\mathbb {R}})$ and an element
$\Omega \subseteq P_{\mathbb {Q}}({\mathbb {R}})$ and an element ![]() $a\in A^+$ such that
$a\in A^+$ such that
We will always assume that ![]() $\Omega \subseteq H_{\mathbb {Q}}({\mathbb {R}})$ and that
$\Omega \subseteq H_{\mathbb {Q}}({\mathbb {R}})$ and that ![]() $\Omega$ is semialgebraic.
$\Omega$ is semialgebraic.
Usually Siegel sets are defined in ![]() $G_{\mathbb {Q}}({\mathbb {R}})$ or in
$G_{\mathbb {Q}}({\mathbb {R}})$ or in ![]() $X=G_{\mathbb {Q}}({\mathbb {R}})/K$. Working with geometric Hecke orbits as defined in Definition 2.3, we use the variety
$X=G_{\mathbb {Q}}({\mathbb {R}})/K$. Working with geometric Hecke orbits as defined in Definition 2.3, we use the variety ![]() $W({\mathbb {R}})^+=G({\mathbb {R}})/Z_G(M)({\mathbb {R}})$. We can view
$W({\mathbb {R}})^+=G({\mathbb {R}})/Z_G(M)({\mathbb {R}})$. We can view ![]() $W({\mathbb {R}})^+$ as an intermediary space in the sequence of maps
$W({\mathbb {R}})^+$ as an intermediary space in the sequence of maps ![]() $G({\mathbb {R}})\to W=G({\mathbb {R}})/Z_G(M)({\mathbb {R}}) \to X$. The following definition allows us to work with Siegel sets in a greater generality.
$G({\mathbb {R}})\to W=G({\mathbb {R}})/Z_G(M)({\mathbb {R}}) \to X$. The following definition allows us to work with Siegel sets in a greater generality.
Definition 5.11 Let ![]() $Z$ be a compact subgroup of
$Z$ be a compact subgroup of ![]() $K$, and
$K$, and ![]() $W=G_{{\mathbb {R}}}/Z$. We define a
$W=G_{{\mathbb {R}}}/Z$. We define a ![]() ${\mathbb {Q}}$-Siegel set
${\mathbb {Q}}$-Siegel set ![]() $\mathfrak {S}_W$ with respect to
$\mathfrak {S}_W$ with respect to ![]() $P_{\mathbb {Q}}$ and
$P_{\mathbb {Q}}$ and ![]() $x$ in
$x$ in ![]() $W^+:=G_{{\mathbb {R}}}({\mathbb {R}})/Z({\mathbb {R}})$ to be the image of
$W^+:=G_{{\mathbb {R}}}({\mathbb {R}})/Z({\mathbb {R}})$ to be the image of ![]() ${\mathbb {Q}}$-Siegel set
${\mathbb {Q}}$-Siegel set ![]() $\mathfrak {S}$ in
$\mathfrak {S}$ in ![]() $G_{\mathbb {Q}}({\mathbb {R}})$ with respect to
$G_{\mathbb {Q}}({\mathbb {R}})$ with respect to ![]() $P_{\mathbb {Q}}$ and
$P_{\mathbb {Q}}$ and ![]() $x$.
$x$.
We note that if ![]() $Z$ is defined over
$Z$ is defined over ![]() ${\mathbb {Q}}$ then so is
${\mathbb {Q}}$ then so is ![]() $W$ and we can consider the subset
$W$ and we can consider the subset ![]() $W^+({\mathbb {Q}})\cap \mathfrak {S}_W$.
$W^+({\mathbb {Q}})\cap \mathfrak {S}_W$.
5.4 Divergence in Siegel sets
In the rest of this section we use the notation ![]() $G=G_{\mathbb {Q}}$.
$G=G_{\mathbb {Q}}$.
5.4.1
We say that an infinite sequence, in an appropriate topological space, is divergent if it does not contain an infinite convergent subsequence. A continuous map is proper if it maps divergent sequences to divergent sequences.
5.4.2
We will use the closure of a Siegel set.
Proposition 5.12 Consider ![]() $\mathfrak {S}=\Omega \cdot A^+_{\geq 0}\cdot a\cdot K_{\infty }$ as in Definition 5.10.
$\mathfrak {S}=\Omega \cdot A^+_{\geq 0}\cdot a\cdot K_{\infty }$ as in Definition 5.10.
Then its closure in ![]() $G({\mathbb {R}})$ is given by
$G({\mathbb {R}})$ is given by
and ![]() $\overline {\mathfrak {S}}$ is contained in a
$\overline {\mathfrak {S}}$ is contained in a ![]() ${\mathbb {Q}}$-Siegel set
${\mathbb {Q}}$-Siegel set ![]() $\mathfrak {S}'$ in
$\mathfrak {S}'$ in ![]() $G({\mathbb {R}})$ with respect to
$G({\mathbb {R}})$ with respect to ![]() $P$ and
$P$ and ![]() $x$.
$x$.
Proof. The set ![]() $\mathfrak {S}$ is obviously dense in the right-hand side of (33). It is the image of the proper map in Lemma 5.13, and thus it is a closed subset in
$\mathfrak {S}$ is obviously dense in the right-hand side of (33). It is the image of the proper map in Lemma 5.13, and thus it is a closed subset in ![]() $G({\mathbb {R}})$. This proves the first assertion. Let
$G({\mathbb {R}})$. This proves the first assertion. Let ![]() $U$ be a nonempty relatively compact semialgebraic open neighbourhood of
$U$ be a nonempty relatively compact semialgebraic open neighbourhood of ![]() $1$ in
$1$ in ![]() $H({\mathbb {R}})$, for instance a small euclidean open ball in a faithful representation
$H({\mathbb {R}})$, for instance a small euclidean open ball in a faithful representation ![]() $H\to GL(N)$. Then
$H\to GL(N)$. Then ![]() $\Omega '=U\cdot \overline {\Omega }$ is an open relatively compact semialgebraic open neighbourhood of
$\Omega '=U\cdot \overline {\Omega }$ is an open relatively compact semialgebraic open neighbourhood of ![]() $\overline {\Omega }$ in
$\overline {\Omega }$ in ![]() $H({\mathbb {R}})$, and the Siegel set
$H({\mathbb {R}})$, and the Siegel set ![]() $\Omega '\cdot A^+_{\geq 0}\cdot a\cdot K$ contains
$\Omega '\cdot A^+_{\geq 0}\cdot a\cdot K$ contains ![]() $\overline {\mathfrak {S}}$.
$\overline {\mathfrak {S}}$.
We used the following.
Lemma 5.13 The map
is proper.
Proof. It suffices to prove that the image of every divergent sequence in the left-hand side is not a convergent sequence in the right-hand side. We prove the contrapositive.
Let ![]() $(\omega _n, a_n, k_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ be a sequence in the left-hand side such that
$(\omega _n, a_n, k_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ be a sequence in the left-hand side such that ![]() $(\omega _n\cdot a_n\cdot k_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ is a convergent sequence in
$(\omega _n\cdot a_n\cdot k_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ is a convergent sequence in ![]() $G({\mathbb {R}})$. Because
$G({\mathbb {R}})$. Because ![]() $\overline {\Omega }$ and
$\overline {\Omega }$ and ![]() $K$ are compact, after possibly extracting a subsequence we may assume that
$K$ are compact, after possibly extracting a subsequence we may assume that ![]() $(\omega _n)_{n\in {\mathbb {Z}}_{\geq 1}}$ and
$(\omega _n)_{n\in {\mathbb {Z}}_{\geq 1}}$ and ![]() $(k_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ are convergent sequences. It follows that
$(k_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ are convergent sequences. It follows that ![]() $(a_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ is a convergent subsequence. We recall that
$(a_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ is a convergent subsequence. We recall that ![]() $(\alpha _1,\ldots,\alpha _r):A^+\to {{\mathbb {R}}_{>0}}^r$ is an isomorphism. It follows that
$(\alpha _1,\ldots,\alpha _r):A^+\to {{\mathbb {R}}_{>0}}^r$ is an isomorphism. It follows that ![]() $A^+_{\geq 0}$ is closed in
$A^+_{\geq 0}$ is closed in ![]() $A^+$. Because
$A^+$. Because ![]() $A({\mathbb {R}})$ is a closed subgroup of
$A({\mathbb {R}})$ is a closed subgroup of ![]() $G({\mathbb {R}})$, that
$G({\mathbb {R}})$, that ![]() $A^+$ is a closed subgroup of
$A^+$ is a closed subgroup of ![]() $A({\mathbb {R}})$, this
$A({\mathbb {R}})$, this ![]() $A_{\geq 0}^+$ is closed in
$A_{\geq 0}^+$ is closed in ![]() $G({\mathbb {R}})$. One deduces that
$G({\mathbb {R}})$. One deduces that ![]() $A_{\geq 0}^+\cdot a$ is closed in
$A_{\geq 0}^+\cdot a$ is closed in ![]() $G({\mathbb {R}})$ and that the limit of
$G({\mathbb {R}})$ and that the limit of ![]() $(a_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ in
$(a_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ in ![]() $G({\mathbb {R}})$ belongs to
$G({\mathbb {R}})$ belongs to ![]() $A_{\geq 0}^+\cdot a$.
$A_{\geq 0}^+\cdot a$.
We proved that the original sequence ![]() $(\omega _n, a_n, k_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ contains a convergent infinite subsequence. Thus, it is not a divergent sequence.
$(\omega _n, a_n, k_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ contains a convergent infinite subsequence. Thus, it is not a divergent sequence.
These results have the following consequence.
Corollary 5.14 A sequence ![]() $(\omega _n\cdot a_n\cdot k_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ is divergent in
$(\omega _n\cdot a_n\cdot k_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ is divergent in ![]() $\overline {\mathfrak {S}}$ if and only if
$\overline {\mathfrak {S}}$ if and only if ![]() $a_n$ is divergent in
$a_n$ is divergent in ![]() $A^+_{\geq 0}$.
$A^+_{\geq 0}$.
Proof. Because ![]() $\overline {\mathfrak {S}}$ is closed,
$\overline {\mathfrak {S}}$ is closed, ![]() $(\omega _n\cdot a_n\cdot k_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ is also divergent in
$(\omega _n\cdot a_n\cdot k_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ is also divergent in ![]() $G({\mathbb {R}})$. It follows that the sequence
$G({\mathbb {R}})$. It follows that the sequence ![]() $(\omega _n, a_n, k_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ contains no convergent subsequence. Because
$(\omega _n, a_n, k_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ contains no convergent subsequence. Because ![]() $\overline {\Omega }$ and
$\overline {\Omega }$ and ![]() $K$ are compact, the projection map
$K$ are compact, the projection map
is proper. It follows that the image sequence ![]() $(a_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ is divergent in
$(a_n)_{n\in {\mathbb {Z}}_{\geq 1}}$ is divergent in ![]() $A^+_{\geq 0}\cdot a$.
$A^+_{\geq 0}\cdot a$.
5.4.3
Let ![]() $P_{1},\ldots,P_{r}$ be the maximal
$P_{1},\ldots,P_{r}$ be the maximal ![]() ${\mathbb {Q}}$-defined properFootnote 13 parabolic subgroups of
${\mathbb {Q}}$-defined properFootnote 13 parabolic subgroups of ![]() $G$ containing
$G$ containing ![]() $P$. We denote by
$P$. We denote by ![]() $N_{i}$ their unipotent radicals, and
$N_{i}$ their unipotent radicals, and ![]() $\mathfrak {n}_i$ the (
$\mathfrak {n}_i$ the (![]() ${\mathbb {Q}}$-linear) Lie algebra of
${\mathbb {Q}}$-linear) Lie algebra of ![]() $N_{i}$. The adjoint representation of
$N_{i}$. The adjoint representation of ![]() $G$ induces an action of
$G$ induces an action of ![]() $G$ on the
$G$ on the ![]() ${\mathbb {Q}}$-vector space
${\mathbb {Q}}$-vector space ![]() $V_i=\bigwedge ^{\dim (N_i)}\mathfrak {g}$. Then the
$V_i=\bigwedge ^{\dim (N_i)}\mathfrak {g}$. Then the ![]() ${\mathbb {Q}}$-vector subspace
${\mathbb {Q}}$-vector subspace ![]() $\bigwedge ^{\dim (N_i)}\mathfrak {n}_i\leq V_i$ is of dimension
$\bigwedge ^{\dim (N_i)}\mathfrak {n}_i\leq V_i$ is of dimension ![]() $1$, and we choose a generator
$1$, and we choose a generator ![]() $\eta _i$ of this
$\eta _i$ of this ![]() ${\mathbb {Q}}$-line.
${\mathbb {Q}}$-line.
Then the ![]() ${\mathbb {R}}$-line
${\mathbb {R}}$-line ![]() ${\mathbb {R}} \cdot \eta _i$ is an eigenspace of
${\mathbb {R}} \cdot \eta _i$ is an eigenspace of ![]() $A$ acting on
$A$ acting on ![]() $V_i\otimes {\mathbb {R}}$, and this eigenspace is defined over
$V_i\otimes {\mathbb {R}}$, and this eigenspace is defined over ![]() ${\mathbb {Q}}$. Let
${\mathbb {Q}}$. Let ![]() $\chi _i$ be the corresponding eigencharacters of
$\chi _i$ be the corresponding eigencharacters of ![]() $A$: we have
$A$: we have
For ![]() $1\leq i\leq r$ the
$1\leq i\leq r$ the ![]() $\chi _i$ are positive multiples
$\chi _i$ are positive multiples ![]() $k_1\cdot \omega _1,\ldots,k_r\cdot \omega _r$ of the (relative) fundamental weightsFootnote 14
$k_1\cdot \omega _1,\ldots,k_r\cdot \omega _r$ of the (relative) fundamental weightsFootnote 14 ![]() $\omega _1,\ldots,\omega _r\in X(A)\otimes {\mathbb {Q}}$. In particular,
$\omega _1,\ldots,\omega _r\in X(A)\otimes {\mathbb {Q}}$. In particular,
One knows that the fundamental weights are positive ![]() ${\mathbb {Q}}$-linear combinations of
${\mathbb {Q}}$-linear combinations of ![]() $\alpha _i$ and that they form a basis of
$\alpha _i$ and that they form a basis of ![]() $X(A)\otimes {\mathbb {Q}}$. The same holds for
$X(A)\otimes {\mathbb {Q}}$. The same holds for ![]() $\chi _i$. We deduce the following.
$\chi _i$. We deduce the following.
Lemma 5.15 Let ![]() $(a_n)_{n\in {\mathbb {Z}}_{\geq 0}}$ be a sequence in
$(a_n)_{n\in {\mathbb {Z}}_{\geq 0}}$ be a sequence in ![]() $A^+_{\geq 0}\cdot a$. Then the sequence is divergent (no infinite subsequence is convergent) if and only if
$A^+_{\geq 0}\cdot a$. Then the sequence is divergent (no infinite subsequence is convergent) if and only if
Proof. If ![]() $(a_n)_{n\in {\mathbb {Z}}_{\geq 0}}$ contains a convergent infinite subsequence, then the sequence
$(a_n)_{n\in {\mathbb {Z}}_{\geq 0}}$ contains a convergent infinite subsequence, then the sequence ![]() $(\min _{1\leq i\leq r} \chi _i(a_n)^{-1})_{n\in {\mathbb {Z}}_{\geq 0}}$ contains a convergent infinite subsequence in
$(\min _{1\leq i\leq r} \chi _i(a_n)^{-1})_{n\in {\mathbb {Z}}_{\geq 0}}$ contains a convergent infinite subsequence in ![]() ${\mathbb {R}}_{>0}$ and we cannot have (36).
${\mathbb {R}}_{>0}$ and we cannot have (36).
This proves one implication and we now prove the other.
Assume that (36) fails. Equivalently,
After possibly extracting a subsequence, we have
Because the ![]() $a_n$ belong to
$a_n$ belong to ![]() $A^+_{\geq 0}\cdot a$ we have
$A^+_{\geq 0}\cdot a$ we have ![]() $\sup _{n\in {\mathbb {Z}}_{\geq 0}}\alpha _i(a_n)^{-1}\leq \alpha _i(a)^{-1}$ for every
$\sup _{n\in {\mathbb {Z}}_{\geq 0}}\alpha _i(a_n)^{-1}\leq \alpha _i(a)^{-1}$ for every ![]() $1\leq i\leq r$. Because the
$1\leq i\leq r$. Because the ![]() $\chi _i$ are positive linear combination of the
$\chi _i$ are positive linear combination of the ![]() $\alpha _i$, the
$\alpha _i$, the ![]() $\chi _i(a_n)^{-1}$ are bounded above. According to (37) they are bounded below in
$\chi _i(a_n)^{-1}$ are bounded above. According to (37) they are bounded below in ![]() ${\mathbb {R}}_{>0}$. Because the
${\mathbb {R}}_{>0}$. Because the ![]() $\chi _i$ form a basis of
$\chi _i$ form a basis of ![]() $X(A)\otimes {\mathbb {Q}}$, the
$X(A)\otimes {\mathbb {Q}}$, the ![]() $\alpha _i$ are linear combination of the
$\alpha _i$ are linear combination of the ![]() $\chi _i$. Hence, the
$\chi _i$. Hence, the ![]() $\alpha _i(a_n)$ are bounded above and below in
$\alpha _i(a_n)$ are bounded above and below in ![]() ${\mathbb {R}}_{>0}$. Equivalently
${\mathbb {R}}_{>0}$. Equivalently ![]() $(a_n)_{n\in {\mathbb {Z}}_{\geq 0}}$ is bounded in
$(a_n)_{n\in {\mathbb {Z}}_{\geq 0}}$ is bounded in ![]() $A^+$. Hence
$A^+$. Hence ![]() $(a_n)_{n\in {\mathbb {Z}}_{\geq 0}}$ is not divergent.
$(a_n)_{n\in {\mathbb {Z}}_{\geq 0}}$ is not divergent.
This proves the other implication.
5.5 Height on Siegel sets
The following statement is the main objective of § 5.
Theorem 5.16 Let ![]() $\mathfrak {S}_W$ as in Definition 5.11 with
$\mathfrak {S}_W$ as in Definition 5.11 with ![]() $Z$ defined over
$Z$ defined over ![]() ${\mathbb {Q}}$, let
${\mathbb {Q}}$, let ![]() $\iota :G/Z\to {\mathbb {A}}_{\mathbb {Q}}^N$ be an affine embedding and let
$\iota :G/Z\to {\mathbb {A}}_{\mathbb {Q}}^N$ be an affine embedding and let ![]() $H_W=H_{{\mathbb {R}}}\cdot H_{f}$ be as in (19). Then, as functions
$H_W=H_{{\mathbb {R}}}\cdot H_{f}$ be as in (19). Then, as functions ![]() $\overline {\mathfrak {S}_W}\cap W({\mathbb {Q}})\to {\mathbb {R}}_{\geq 0}$ we have
$\overline {\mathfrak {S}_W}\cap W({\mathbb {Q}})\to {\mathbb {R}}_{\geq 0}$ we have
This will be deduced from Proposition 5.9. We first construct the map ![]() $p$ to which we apply the proposition, and then verify the assumptions of the proposition.
$p$ to which we apply the proposition, and then verify the assumptions of the proposition.
5.5.1 Construction of the morphism  $p$
$p$
Let ![]() $\eta _i\in V_i=\bigwedge ^{\dim {\mathfrak {n}_i}} \mathfrak {g}$ and
$\eta _i\in V_i=\bigwedge ^{\dim {\mathfrak {n}_i}} \mathfrak {g}$ and ![]() $\chi _i$ be as in § 5.4.3.
$\chi _i$ be as in § 5.4.3.
For each ![]() $1\leq i\leq r$, we choose a positive-definite quadratic form
$1\leq i\leq r$, we choose a positive-definite quadratic form
We denote by ![]() $dz$ the Haar probability measure on
$dz$ the Haar probability measure on ![]() $Z({\mathbb {R}})$ we define the real quadratic form
$Z({\mathbb {R}})$ we define the real quadratic form
The following is central in our argument.
Lemma 5.17 The quadratic form ![]() $Q_i$ is invariant under
$Q_i$ is invariant under ![]() $Z({\mathbb {R}})$, is positive definite, and is defined over
$Z({\mathbb {R}})$, is positive definite, and is defined over ![]() ${\mathbb {Q}}$.
${\mathbb {Q}}$.
Proof. The two first properties are immediate from (38). We prove that ![]() $Q_i$ is defined over
$Q_i$ is defined over ![]() ${\mathbb {Q}}$. Let
${\mathbb {Q}}$. Let ![]() $V$ be the
$V$ be the ![]() ${\mathbb {Q}}$-vector space of quadratic forms, as a representation of
${\mathbb {Q}}$-vector space of quadratic forms, as a representation of ![]() $Z$, and
$Z$, and ![]() $V^Z$ be the subspace of elements fixed by
$V^Z$ be the subspace of elements fixed by ![]() $Z$. As
$Z$. As ![]() $Z({\mathbb {R}})$ is compact, the
$Z({\mathbb {R}})$ is compact, the ![]() ${\mathbb {Q}}$-group
${\mathbb {Q}}$-group ![]() $Z$ is reductive, and there is a
$Z$ is reductive, and there is a ![]() $Z$-stable
$Z$-stable ![]() ${\mathbb {Q}}$-subspace
${\mathbb {Q}}$-subspace ![]() $W$ such that we can decompose
$W$ such that we can decompose
Let us write correspondingly
with ![]() $Q'_Z$ in
$Q'_Z$ in ![]() $V^Z$ and
$V^Z$ and ![]() $Q'_W$ in
$Q'_W$ in ![]() $W$.
$W$.
Because ![]() $Q_Z$ is invariant under
$Q_Z$ is invariant under ![]() $Z({\mathbb {R}})$ and
$Z({\mathbb {R}})$ and ![]() $W\otimes {\mathbb {R}}$ is stable under
$W\otimes {\mathbb {R}}$ is stable under ![]() $Z({\mathbb {R}})$,
$Z({\mathbb {R}})$,
By construction, ![]() $\int _{Z({\mathbb {R}})} z \cdot Q_W\,d z$ is fixed by
$\int _{Z({\mathbb {R}})} z \cdot Q_W\,d z$ is fixed by ![]() $Z({\mathbb {R}})$ and, thus, it belongs to
$Z({\mathbb {R}})$ and, thus, it belongs to ![]() $W\otimes {\mathbb {R}}\cap V^Z\otimes {\mathbb {R}}=\{0\}$. We compute
$W\otimes {\mathbb {R}}\cap V^Z\otimes {\mathbb {R}}=\{0\}$. We compute
Because ![]() $Q_Z$ is defined over
$Q_Z$ is defined over ![]() ${\mathbb {Q}}$, so is
${\mathbb {Q}}$, so is ![]() $Q_i$.
$Q_i$.
We can now define ![]() $p:W\to {\mathbb {A}}_{\mathbb {Q}}^r$ by
$p:W\to {\mathbb {A}}_{\mathbb {Q}}^r$ by
As the ![]() $Q_i$ are defined over
$Q_i$ are defined over ![]() ${\mathbb {Q}}$ so is
${\mathbb {Q}}$ so is ![]() $p$, and as the
$p$, and as the ![]() $Q_i$ are
$Q_i$ are ![]() $Z$-invariant,
$Z$-invariant, ![]() $p$ is well defined.
$p$ is well defined.
5.5.2 Properties of the morphism  $p$
$p$
Our next task is to verify the assumptions of Proposition 5.9.
(i) We have
 $p(\overline {\mathfrak {S}_W}) \subset ({\mathbb {R}}^\times )^r$.
$p(\overline {\mathfrak {S}_W}) \subset ({\mathbb {R}}^\times )^r$.(ii) As a map
 $\overline {\mathfrak {S}_W}\to ({\mathbb {R}}^\times )^r$,
$\overline {\mathfrak {S}_W}\to ({\mathbb {R}}^\times )^r$,  $p|_{\overline {\mathfrak {S}_W}}$ is proper with respect to the real topologies.
$p|_{\overline {\mathfrak {S}_W}}$ is proper with respect to the real topologies.(iii) The image
 $p(\overline {\mathfrak {S}})$ is bounded in
$p(\overline {\mathfrak {S}})$ is bounded in  ${\mathbb {R}}^r$.
${\mathbb {R}}^r$.
Proof of assumption (i) Every point of ![]() $\overline {\mathfrak {S}_W}$ is of the form
$\overline {\mathfrak {S}_W}$ is of the form ![]() $gZ$ with
$gZ$ with ![]() $g\in G({\mathbb {R}})$. The vector
$g\in G({\mathbb {R}})$. The vector ![]() $g\cdot \eta _i$ is thus in
$g\cdot \eta _i$ is thus in ![]() $V_i\otimes {\mathbb {R}}$. As
$V_i\otimes {\mathbb {R}}$. As ![]() $\eta _i\neq 0$ and
$\eta _i\neq 0$ and ![]() $g$ is invertible,
$g$ is invertible, ![]() $g^{-1}\cdot \eta _i\neq 0$. As
$g^{-1}\cdot \eta _i\neq 0$. As ![]() $Q_i$ is positive definite by Lemma 5.17, we have
$Q_i$ is positive definite by Lemma 5.17, we have ![]() $p_i(g):=Q_i(g^{-1}\eta _i)\in {\mathbb {R}}_{>0}$.
$p_i(g):=Q_i(g^{-1}\eta _i)\in {\mathbb {R}}_{>0}$.
We will use that there exists ![]() $C\in {\mathbb {R}}_{>0}$ such that for every
$C\in {\mathbb {R}}_{>0}$ such that for every ![]() $1\leq i\leq r$,
$1\leq i\leq r$,
Proof of (40) We write ![]() $\sigma =h\cdot a\cdot \alpha \cdot k$. By (32), we have
$\sigma =h\cdot a\cdot \alpha \cdot k$. By (32), we have ![]() $h^{-1}\cdot \eta _i=\pm \eta _i$. Thus,
$h^{-1}\cdot \eta _i=\pm \eta _i$. Thus,
Because ![]() $K$ is compact there exists a
$K$ is compact there exists a ![]() $K$-invariant euclidean norm
$K$-invariant euclidean norm ![]() $\lVert - \rVert$ on
$\lVert - \rVert$ on ![]() $V_i\otimes {\mathbb {R}}$. The two norms
$V_i\otimes {\mathbb {R}}$. The two norms ![]() $\sqrt {Q_i}$ and
$\sqrt {Q_i}$ and ![]() $\lVert - \rVert$ on
$\lVert - \rVert$ on ![]() $V_i\otimes {\mathbb {R}}$ are comparable: there is
$V_i\otimes {\mathbb {R}}$ are comparable: there is ![]() $C_i\in {\mathbb {R}}_{>0}$ such that for any
$C_i\in {\mathbb {R}}_{>0}$ such that for any ![]() $v\in V_i\otimes {\mathbb {R}}$,
$v\in V_i\otimes {\mathbb {R}}$,
We deduce (40) with ![]() $C=\max _{i\in \{1;\ldots ;r\}} C_i\cdot \lVert a^{-1}\cdot \eta _i \rVert ^2$ from
$C=\max _{i\in \{1;\ldots ;r\}} C_i\cdot \lVert a^{-1}\cdot \eta _i \rVert ^2$ from
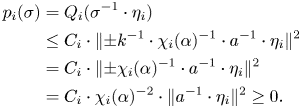 \begin{align*} p_i(\sigma)&=Q_i(\sigma^{-1}\cdot \eta_i)\\ &\leq C_i\cdot \lVert \pm k^{-1} \cdot \chi_i(\alpha)^{-1}\cdot a^{-1}\cdot \eta_i \rVert^2\\ &= C_i\cdot \lVert \pm\chi_i(\alpha)^{-1}\cdot a^{-1}\cdot \eta_i \rVert^2\\ &=C_i\cdot \chi_i(\alpha)^{-2} \cdot \lVert a^{-1}\cdot \eta_i \rVert^2\geq 0. \end{align*}
\begin{align*} p_i(\sigma)&=Q_i(\sigma^{-1}\cdot \eta_i)\\ &\leq C_i\cdot \lVert \pm k^{-1} \cdot \chi_i(\alpha)^{-1}\cdot a^{-1}\cdot \eta_i \rVert^2\\ &= C_i\cdot \lVert \pm\chi_i(\alpha)^{-1}\cdot a^{-1}\cdot \eta_i \rVert^2\\ &=C_i\cdot \chi_i(\alpha)^{-2} \cdot \lVert a^{-1}\cdot \eta_i \rVert^2\geq 0. \end{align*}
Proof of assumption (ii) For a divergent sequence ![]() $\sigma _n=\omega _n a\cdot \alpha _n k_n$ in
$\sigma _n=\omega _n a\cdot \alpha _n k_n$ in ![]() $\overline {\mathfrak {S}_W}$, Corollary 5.14 and Lemma 5.15 imply that
$\overline {\mathfrak {S}_W}$, Corollary 5.14 and Lemma 5.15 imply that ![]() $\min _{1\leq i \leq r} \chi _i(\alpha _n) \to 0$. Using (40), we deduce that
$\min _{1\leq i \leq r} \chi _i(\alpha _n) \to 0$. Using (40), we deduce that
and, thus, ![]() $p(\omega _n a_n k_n)$ is divergent in
$p(\omega _n a_n k_n)$ is divergent in ![]() ${{\mathbb {R}}^\times }^r$. This proves the properness.
${{\mathbb {R}}^\times }^r$. This proves the properness.
Proof of assumption (iii) For ![]() $\sigma =h\cdot \alpha \cdot a\cdot k\in \overline {\mathfrak {S}}$, we have
$\sigma =h\cdot \alpha \cdot a\cdot k\in \overline {\mathfrak {S}}$, we have ![]() $0\leq \chi _1(\alpha ),\ldots,\chi _r(\alpha )\leq 1$ by (35), and deduce from (40) that
$0\leq \chi _1(\alpha ),\ldots,\chi _r(\alpha )\leq 1$ by (35), and deduce from (40) that
We now use Proposition 5.9 with ![]() $\mathfrak {S}=\overline {\mathfrak {S}_W}$. This concludes the proof of Theorem 5.16.
$\mathfrak {S}=\overline {\mathfrak {S}_W}$. This concludes the proof of Theorem 5.16.
6. Weak adelic Mumford–Tate hypothesis and lower bounds on Galois orbits
This section is central to the proof of the André–Pink–Zannier conjecture under our assumptions (Theorem 1.2). In this section, we state a precise form of the ‘weak adelic Mumford–Tate hypothesis’.
We then translate lower and upper bounds on adelic orbits of Appendices B and C into estimates for sizes of the Galois orbits in terms of the height functions of § 4 (when the Mumford–Tate hypothesis holds).
For simplicity in the following we refer to the ‘Mumford–Tate hypothesis’ or simply ‘MT hypothesis’.
Finally, we provide some natural functoriality properties of the Mumford–Tate hypothesis, which will be needed for the reduction steps in the proof of our main theorem.
6.1 The Mumford–Tate hypothesis
We start with a property applicable in more general situations.
Definition 6.1 Let ![]() $M$ be a linear algebraic group over
$M$ be a linear algebraic group over ![]() ${\mathbb {Q}}$, let
${\mathbb {Q}}$, let ![]() $K_M\leq M({\mathbb {A}}_f)$ be a compact open subgroup, and let
$K_M\leq M({\mathbb {A}}_f)$ be a compact open subgroup, and let ![]() $U\leq M({\mathbb {A}}_f)$ be a compact subgroup.
$U\leq M({\mathbb {A}}_f)$ be a compact subgroup.
We say that ![]() $U$ is MT in
$U$ is MT in ![]() $M$ if the indices
$M$ if the indices
are finite and uniformly bounded as ![]() $p$ ranges through primes, where
$p$ ranges through primes, where ![]() $M({\mathbb {Q}}_p)\leq M({\mathbb {A}}_f)$ is understood as a factor subgroup of
$M({\mathbb {Q}}_p)\leq M({\mathbb {A}}_f)$ is understood as a factor subgroup of ![]() $M({\mathbb {A}}_f)$.
$M({\mathbb {A}}_f)$.
Note that the definition does not depend on the choice of ![]() $K_M$, as any two compact open subgroups are commensurable. We may always enlarge
$K_M$, as any two compact open subgroups are commensurable. We may always enlarge ![]() $K_M$ so that it takes the product form
$K_M$ so that it takes the product form ![]() $K_M=\prod _p K_p$ in which case the indices become
$K_M=\prod _p K_p$ in which case the indices become
Likewise if ![]() $U'\leq M({\mathbb {A}}_f)$ is a compact subgroup commensurable to
$U'\leq M({\mathbb {A}}_f)$ is a compact subgroup commensurable to ![]() $U$, then
$U$, then ![]() $U$ is MT in
$U$ is MT in ![]() $M$ if and only if
$M$ if and only if ![]() $U'$ is MT in
$U'$ is MT in ![]() $M$. Note (and this is very important) that the condition that
$M$. Note (and this is very important) that the condition that ![]() $U$ is MT in
$U$ is MT in ![]() $M$ does not imply that
$M$ does not imply that ![]() $U$ is open in
$U$ is open in ![]() $M({\mathbb {A}}_f)$.
$M({\mathbb {A}}_f)$.
The following observation is an immediate consequence of the definition.
Lemma 6.2 In the Definition 6.1, let
Then ![]() $U$ is MT in
$U$ is MT in ![]() $M$ if and only if
$M$ if and only if ![]() $U'$ is MT in
$U'$ is MT in ![]() $M$.
$M$.
We specialise the above definition to the context of images of Galois representations.
Definition 6.3 Let ![]() $(G,X)$ be a Shimura datum, let
$(G,X)$ be a Shimura datum, let ![]() $x_0\in X$ and let
$x_0\in X$ and let ![]() $M$ be the Mumford–Tate group of
$M$ be the Mumford–Tate group of ![]() $x_0$, let
$x_0$, let ![]() $\rho _{x_0}$ be a Galois representation for
$\rho _{x_0}$ be a Galois representation for ![]() $x_0$ defined over a field
$x_0$ defined over a field ![]() $E$ in the sense of Definition 3.1, and let
$E$ in the sense of Definition 3.1, and let ![]() $U=\rho _{x_0}(Gal(\overline {E}/E))\leq M({\mathbb {A}}_f)$ be the image of
$U=\rho _{x_0}(Gal(\overline {E}/E))\leq M({\mathbb {A}}_f)$ be the image of ![]() $\rho _{x_0}$.
$\rho _{x_0}$.
(i) We say that
 $x_0$ satisfies the MT hypothesis, if
$x_0$ satisfies the MT hypothesis, if  $U$ is MT in
$U$ is MT in  $M$.
$M$.(ii) Let
 $K\leq G({\mathbb {A}}_f)$ be a compact open subgroup, and
$K\leq G({\mathbb {A}}_f)$ be a compact open subgroup, and  $s_0=[x_0,1]\in Sh_K(G,X)$. We say that
$s_0=[x_0,1]\in Sh_K(G,X)$. We say that  $s_0$ satisfies the MT hypothesis if
$s_0$ satisfies the MT hypothesis if  $U$ is MT in
$U$ is MT in  $M$.
$M$.
6.2 Lower bounds for Galois orbits in terms of finite heights under the MT hypothesis
The following statement is an essential ingredient in the proof of the main theorem (see § 7). We also believe it to be of independent interest.
Theorem 6.4 Let ![]() $M$ be a connected reductive group over
$M$ be a connected reductive group over ![]() ${\mathbb {Q}}$ and
${\mathbb {Q}}$ and ![]() $U\leq M({\mathbb {A}}_f)$ be a compact subgroup which is MT in
$U\leq M({\mathbb {A}}_f)$ be a compact subgroup which is MT in ![]() $M$ in the sense of Definition 6.1. We use the notation of Definition 1.7.
$M$ in the sense of Definition 6.1. We use the notation of Definition 1.7.
(i) Let
 $\phi _0:M\to GL(N)$ be a representation over
$\phi _0:M\to GL(N)$ be a representation over  ${\mathbb {Q}}$, and let
${\mathbb {Q}}$, and let  $W$ be the
$W$ be the  $GL(N)$-conjugacy class of
$GL(N)$-conjugacy class of  $\phi _0$. We consider an affine embedding
$\phi _0$. We consider an affine embedding  $\iota :W\to {\mathbb {A}}^N_{{\mathbb {Q}}}$ and the corresponding function
$\iota :W\to {\mathbb {A}}^N_{{\mathbb {Q}}}$ and the corresponding function  $H_f:W({\mathbb {Q}}_f)\to {\mathbb {Z}}_{\geq 1}$ defined by (17). Then, as
$H_f:W({\mathbb {Q}}_f)\to {\mathbb {Z}}_{\geq 1}$ defined by (17). Then, as  $\phi$ ranges through
$\phi$ ranges through  $W({\mathbb {A}}_f)$, we have
(44)
$W({\mathbb {A}}_f)$, we have
(44) \begin{equation} [\phi(U):\phi(U) \cap GL(N,\widehat{{\mathbb{Z}}})] \approx H_f(\phi). \end{equation}
\begin{equation} [\phi(U):\phi(U) \cap GL(N,\widehat{{\mathbb{Z}}})] \approx H_f(\phi). \end{equation}(ii) Let
 $\phi _0:M\to G$ be a morphism of algebraic groups over
$\phi _0:M\to G$ be a morphism of algebraic groups over  ${\mathbb {Q}}$ and let
${\mathbb {Q}}$ and let  $W$ be the
$W$ be the  $G$-conjugacy class of
$G$-conjugacy class of  $\phi _0$. We consider an affine embedding
$\phi _0$. We consider an affine embedding  $\iota :W\to {\mathbb {A}}^N_{{\mathbb {Q}}}$ and the corresponding function
$\iota :W\to {\mathbb {A}}^N_{{\mathbb {Q}}}$ and the corresponding function  $H_f:W({\mathbb {Q}}_f)\to {\mathbb {Z}}_{\geq 1}$ defined by (17). We also consider an open compact subgroup
$H_f:W({\mathbb {Q}}_f)\to {\mathbb {Z}}_{\geq 1}$ defined by (17). We also consider an open compact subgroup  $K\leq G({\mathbb {A}}_f)$. Then, as
$K\leq G({\mathbb {A}}_f)$. Then, as  $\phi$ ranges through
$\phi$ ranges through  $W({\mathbb {A}}_f)$, we have
(45)
$W({\mathbb {A}}_f)$, we have
(45) \begin{equation} [\phi(U):\phi(U) \cap K] \approx H_f(\phi). \end{equation}
\begin{equation} [\phi(U):\phi(U) \cap K] \approx H_f(\phi). \end{equation}
First, let us reduce the second assertion to the first.
Proof. We identify ![]() $G$ with its image by a faithful representation
$G$ with its image by a faithful representation ![]() $G\to GL(N)$. We may replace
$G\to GL(N)$. We may replace ![]() $K$ by a commensurable group, and assume
$K$ by a commensurable group, and assume ![]() $K$ is a maximal compact subgroup of
$K$ is a maximal compact subgroup of ![]() $G({\mathbb {A}}_f)$. For any maximal compact subgroup
$G({\mathbb {A}}_f)$. For any maximal compact subgroup ![]() $K'$ of
$K'$ of ![]() $GL(N,{\mathbb {A}}_f)$ such that
$GL(N,{\mathbb {A}}_f)$ such that ![]() $K\leq K'\leq GL(N,{\mathbb {A}}_f)$, we then have
$K\leq K'\leq GL(N,{\mathbb {A}}_f)$, we then have
We choose such a ![]() $K'$, and, possibly conjugating by an element of
$K'$, and, possibly conjugating by an element of ![]() $GL(N,{\mathbb {Q}})$, we may assume
$GL(N,{\mathbb {Q}})$, we may assume ![]() $K'=GL(N,\widehat {{\mathbb {Z}}})$.
$K'=GL(N,\widehat {{\mathbb {Z}}})$.
Consider ![]() $\phi :M\to G$ in (45). From
$\phi :M\to G$ in (45). From ![]() $\phi (U)\leq G({\mathbb {A}}_f)$ and (46), we deduce
$\phi (U)\leq G({\mathbb {A}}_f)$ and (46), we deduce
We have identified the left-hand side of (47) with the left-hand side of (45).
It will be enough to identify the right-hand sides. We will show that a height function ![]() $H_f$ on the
$H_f$ on the ![]() $GL(N)$-conjugacy class of
$GL(N)$-conjugacy class of ![]() $\phi$, when restricted to the
$\phi$, when restricted to the ![]() $G$-conjugacy class, is a height function on this
$G$-conjugacy class, is a height function on this ![]() $G$-conjugacy class.
$G$-conjugacy class.
If ![]() $H_f:GL(N,{\mathbb {A}}_f)\cdot \phi \to {\mathbb {Z}}_{\geq 1}$ is associated to
$H_f:GL(N,{\mathbb {A}}_f)\cdot \phi \to {\mathbb {Z}}_{\geq 1}$ is associated to ![]() $\iota :GL(N)\cdot \phi \to {\mathbb {A}}^N_{\mathbb {Q}}$, then its restriction to
$\iota :GL(N)\cdot \phi \to {\mathbb {A}}^N_{\mathbb {Q}}$, then its restriction to ![]() $GL(N,{\mathbb {A}}_f)\cdot \phi$ is associated to
$GL(N,{\mathbb {A}}_f)\cdot \phi$ is associated to ![]() $\iota ':G\cdot \phi \to GL(N)\cdot \phi \to {\mathbb {A}}^N_{\mathbb {Q}}$, provided
$\iota ':G\cdot \phi \to GL(N)\cdot \phi \to {\mathbb {A}}^N_{\mathbb {Q}}$, provided ![]() $\iota '$ is a closed embedding.
$\iota '$ is a closed embedding.
It is equivalent to proving that ![]() $G\cdot \phi \subseteq GL(N,{\mathbb {A}}_f)\cdot \phi$ is Zariski closed.
$G\cdot \phi \subseteq GL(N,{\mathbb {A}}_f)\cdot \phi$ is Zariski closed.
To do this, we choose the map
By assumption, ![]() $M$ is Zariski connected. This map is thus injective. As
$M$ is Zariski connected. This map is thus injective. As ![]() $M$ is reductive, according to [Reference RichardsonRic88, Theorem 3.6], the image of
$M$ is reductive, according to [Reference RichardsonRic88, Theorem 3.6], the image of ![]() $G\cdot \phi$ is closed in
$G\cdot \phi$ is closed in ![]() $\mbox {Hom}(\mathfrak {m},\mathfrak {gl}(N))$, and thus
$\mbox {Hom}(\mathfrak {m},\mathfrak {gl}(N))$, and thus ![]() $G\cdot \phi \subseteq GL(N,{\mathbb {A}}_f)\cdot \phi$ is Zariski closed.
$G\cdot \phi \subseteq GL(N,{\mathbb {A}}_f)\cdot \phi$ is Zariski closed.
We now reduce the first assertion to Corollary B.2, Theorems B.1 and B.4.
Proof. Writing ![]() $K=GL(N,\widehat {{\mathbb {Z}}})$ for short, we may rewrite the left-hand side of (44) as
$K=GL(N,\widehat {{\mathbb {Z}}})$ for short, we may rewrite the left-hand side of (44) as
Theorem C.1 implies ![]() $[\phi (U):\phi (U) \cap K] \preccurlyeq H_f(\phi )$. We now prove
$[\phi (U):\phi (U) \cap K] \preccurlyeq H_f(\phi )$. We now prove ![]() $H_f(\phi ) \preccurlyeq [\phi (U):\phi (U) \cap K]$.
$H_f(\phi ) \preccurlyeq [\phi (U):\phi (U) \cap K]$.
It is enough to obtain a lower bound after replacing ![]() $U$ by the smaller group
$U$ by the smaller group ![]() $U'\leq U$ as in Lemma 6.2: without loss of generality we may assume
$U'\leq U$ as in Lemma 6.2: without loss of generality we may assume ![]() $U=U'$. We thus assume that
$U=U'$. We thus assume that ![]() $U=\prod _p U_p$ as in (43).
$U=\prod _p U_p$ as in (43).
The left-hand side is the product of ![]() $K_p=GL(N,{\mathbb {Z}}_p)$, hence we have
$K_p=GL(N,{\mathbb {Z}}_p)$, hence we have
We apply Definition 6.1 for ![]() $K_M=M(\widehat {{\mathbb {Z}}})=M({\mathbb {A}}_f)\cap GL(d,\widehat {{\mathbb {Z}}})$: the upper bound
$K_M=M(\widehat {{\mathbb {Z}}})=M({\mathbb {A}}_f)\cap GL(d,\widehat {{\mathbb {Z}}})$: the upper bound ![]() $C=\sup _p[M({\mathbb {Z}}_p):U_p]$ is finite. Using (B.6) we have
$C=\sup _p[M({\mathbb {Z}}_p):U_p]$ is finite. Using (B.6) we have
As in the proof of (B.1) of Theorem B.1, we can deduce
Arguing as in the proof of (B.2) and (B.3) of Corollary B.2, we obtain
6.3 Functoriality properties of the MT hypothesis
The following uses general properties of adelic topologies on algebraic groups. A good reference is [Reference Platonov and RapinchukPR94].
Lemma 6.5 Let ![]() $\phi :M\to G$ be a morphism of connected linear algebraic groups over
$\phi :M\to G$ be a morphism of connected linear algebraic groups over ![]() ${\mathbb {Q}}$, and let
${\mathbb {Q}}$, and let ![]() $U\leq M({\mathbb {A}}_f)$ be a compact subgroup.
$U\leq M({\mathbb {A}}_f)$ be a compact subgroup.
(i) If
 $U$ is MT in
$U$ is MT in  $M$, then
$M$, then  $\phi (U)$ is MT in
$\phi (U)$ is MT in  $\phi (M)$.
$\phi (M)$.(ii) If
 $\phi$ is an isogeny onto its image (i.e.
$\phi$ is an isogeny onto its image (i.e.  $\ker (\phi )$ is finite), then
$\ker (\phi )$ is finite), then  $U$ is MT in
$U$ is MT in  $M$ if
$M$ if  $\phi (U)$ is MT in
$\phi (U)$ is MT in  $\phi (M)$.
$\phi (M)$.(iii) We assume
 $M$ is reductive. Let
$M$ is reductive. Let  $ad_M:M\to M^{\rm ad}=M/Z_M(M)$ be the adjoint map, and
$ad_M:M\to M^{\rm ad}=M/Z_M(M)$ be the adjoint map, and  $ab_M:M\to M^{\rm ab}=M/[M,M]$ be the abelianisation map. Then
$ab_M:M\to M^{\rm ab}=M/[M,M]$ be the abelianisation map. Then  $U$ is MT in
$U$ is MT in  $M$ if and only if
$M$ if and only if  $ad_M(U)$ is MT in
$ad_M(U)$ is MT in  $M^{\rm ad}$ and
$M^{\rm ad}$ and  $ab_M(U)$ is MT in
$ab_M(U)$ is MT in  $M^{\rm ab}$.
$M^{\rm ab}$.
The proof of Lemma 6.5 will rely on the following.
Theorem 6.6 Let ![]() $\phi :H\to G$ be an epimorphism of
$\phi :H\to G$ be an epimorphism of ![]() ${\mathbb {Q}}$-algebraic groups and
${\mathbb {Q}}$-algebraic groups and ![]() $C$ be the number of components of
$C$ be the number of components of ![]() $\ker (\phi )$ for the Zariski topology.
$\ker (\phi )$ for the Zariski topology.
(i) Let
 $K\leq H({\mathbb {A}}_f)$ and
$K\leq H({\mathbb {A}}_f)$ and  $K'\leq G({\mathbb {A}}_f)$ be compact open subgroups of the form
$K'\leq G({\mathbb {A}}_f)$ be compact open subgroups of the form  $\prod _p K_p$ and
$\prod _p K_p$ and  $\prod _p K'_p$. Then
$\prod _p K'_p$. Then
 \[ \forall \, p\gg0, \phi(K_p)\leq K'_p\text{ and }[K'_p:\phi(K_p)]\leq C. \]
\[ \forall \, p\gg0, \phi(K_p)\leq K'_p\text{ and }[K'_p:\phi(K_p)]\leq C. \]
(ii) If
 $C=1$, then the map
$C=1$, then the map  $p:H({\mathbb {A}}_f)\to G({\mathbb {A}}_f)$ is open: for any open subgroup
$p:H({\mathbb {A}}_f)\to G({\mathbb {A}}_f)$ is open: for any open subgroup  $K\leq H({\mathbb {A}}_f)$, the image
$K\leq H({\mathbb {A}}_f)$, the image  $\phi (K)$ is open in
$\phi (K)$ is open in  $G({\mathbb {A}}_f)$.
$G({\mathbb {A}}_f)$.
The second assertion, which is [Reference Platonov and RapinchukPR94, p. 296, § 6.2, Proposition 6.5], is a corollary of the first assertion. The first assertion follows from [Reference Platonov and RapinchukPR94, p. 296, § 6.2, Proposition 6.4] and [Reference Platonov and RapinchukPR94, p. 296, § 6.2, Proposition 6.5] (using their exact sequence (6.9) under conditions of their Lemma 6.6).
Let us prove Lemma 6.5(i).
Proof. We choose a maximal compact subgroup ![]() $K_M\leq M({\mathbb {A}}_f)$, and a maximal compact subgroup
$K_M\leq M({\mathbb {A}}_f)$, and a maximal compact subgroup ![]() $K'\leq \phi (M)({\mathbb {A}}_f)$ containing
$K'\leq \phi (M)({\mathbb {A}}_f)$ containing ![]() $\phi (K_M)$. By maximality, they have a product form
$\phi (K_M)$. By maximality, they have a product form ![]() $K_M=\prod _p K_p$ and
$K_M=\prod _p K_p$ and ![]() $K'=\prod _p K'_p$. According to Definition 6.1, there exists
$K'=\prod _p K'_p$. According to Definition 6.1, there exists ![]() $c\in {\mathbb {R}}_{>0}$ such that for all primes
$c\in {\mathbb {R}}_{>0}$ such that for all primes ![]() $p$, we have
$p$, we have ![]() $c\geq [K_p:U_p\cap K_p]$. Applying
$c\geq [K_p:U_p\cap K_p]$. Applying ![]() $\phi$ we deduce
$\phi$ we deduce
Let ![]() $C\in {\mathbb {R}}_{>0}$ be given by Theorem 6.6. Using natural inclusions
$C\in {\mathbb {R}}_{>0}$ be given by Theorem 6.6. Using natural inclusions ![]() $\phi (U_p)\subseteq \phi (U)_p$ and
$\phi (U_p)\subseteq \phi (U)_p$ and ![]() $\phi (K_p)\subseteq K'_p$, we have
$\phi (K_p)\subseteq K'_p$, we have
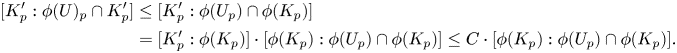 \begin{align} [K'_p:\phi(U)_p\cap K'_p] &\leq [K'_p:\phi(U_p)\cap \phi(K_p)]\nonumber\\ &= [K'_p:\phi(K_p)]\cdot [\phi(K_p):\phi(U_p)\cap \phi(K_p)]\leq C\cdot [\phi(K_p):\phi(U_p)\cap \phi(K_p)]. \end{align}
\begin{align} [K'_p:\phi(U)_p\cap K'_p] &\leq [K'_p:\phi(U_p)\cap \phi(K_p)]\nonumber\\ &= [K'_p:\phi(K_p)]\cdot [\phi(K_p):\phi(U_p)\cap \phi(K_p)]\leq C\cdot [\phi(K_p):\phi(U_p)\cap \phi(K_p)]. \end{align}
Thus, for every prime ![]() $p$, we have
$p$, we have ![]() $[K'_p:\phi (U)_p\cap K'_p]\leq c\cdot C$.
$[K'_p:\phi (U)_p\cap K'_p]\leq c\cdot C$.
We now prove Lemma 6.5(ii).
Proof. We write ![]() $K_M=\prod K_p$ and
$K_M=\prod K_p$ and ![]() $K'=\prod K'_p$ as before.
$K'=\prod K'_p$ as before.
We choose a set of generators ![]() $\phi (u_1),\ldots,\phi (u_k)$ for
$\phi (u_1),\ldots,\phi (u_k)$ for ![]() $\phi (U)_p$ and let
$\phi (U)_p$ and let ![]() $U'\leq U$ be the compact subgroup topologically generated by
$U'\leq U$ be the compact subgroup topologically generated by ![]() $u_i$. Let us prove that
$u_i$. Let us prove that ![]() $k$ can be chosen independently of
$k$ can be chosen independently of ![]() $p$.
$p$.
Proof. For a fixed ![]() $p$ we use assertion (i) of Lemma 6.8 with
$p$ we use assertion (i) of Lemma 6.8 with ![]() $V=\phi (U)_p$. For large
$V=\phi (U)_p$. For large ![]() $p$, the group
$p$, the group ![]() $V':=\exp (p\phi (\mathfrak {m}_{{\mathbb {Z}}_p}))$ and the reduction map
$V':=\exp (p\phi (\mathfrak {m}_{{\mathbb {Z}}_p}))$ and the reduction map ![]() $M({\mathbb {Z}}_p)\to M({\mathbb {F}}_p)$ are well defined and, by assertion (iii) of Lemma 6.8, we have
$M({\mathbb {Z}}_p)\to M({\mathbb {F}}_p)$ are well defined and, by assertion (iii) of Lemma 6.8, we have ![]() $V'\leq V\leq M({\mathbb {Z}}_p)$. Applying the remark from the proof of Proposition 6.7 to the exact sequence
$V'\leq V\leq M({\mathbb {Z}}_p)$. Applying the remark from the proof of Proposition 6.7 to the exact sequence ![]() $1\to V'\to V \to M({\mathbb {F}}_p)$, it follows from Proposition 6.7 for the image of
$1\to V'\to V \to M({\mathbb {F}}_p)$, it follows from Proposition 6.7 for the image of ![]() $V$ and assertion (ii) of Lemma 6.8 for
$V$ and assertion (ii) of Lemma 6.8 for ![]() $V'$.
$V'$.
Let ![]() $F$ be the kernel of
$F$ be the kernel of ![]() $\phi$. This is a finite algebraic group by hypothesis. We define
$\phi$. This is a finite algebraic group by hypothesis. We define ![]() $U'_p=U'\cap M({\mathbb {Q}}_p)$. Then
$U'_p=U'\cap M({\mathbb {Q}}_p)$. Then ![]() $U'_p$ is also the kernel of the map
$U'_p$ is also the kernel of the map
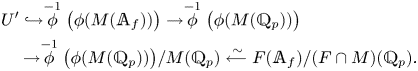 \begin{align} &U'\hookrightarrow \stackrel{-1}{\phi}\big(\phi(M({\mathbb{A}}_f))\big)\to \stackrel{-1}{\phi}\big(\phi(M({\mathbb{Q}}_p))\big)\nonumber\\ &\quad \to \stackrel{-1}{\phi}\big(\phi(M({\mathbb{Q}}_p))\big)/M({\mathbb{Q}}_p)\xleftarrow{\sim} F({\mathbb{A}}_f)/(F\cap M)({\mathbb{Q}}_p). \end{align}
\begin{align} &U'\hookrightarrow \stackrel{-1}{\phi}\big(\phi(M({\mathbb{A}}_f))\big)\to \stackrel{-1}{\phi}\big(\phi(M({\mathbb{Q}}_p))\big)\nonumber\\ &\quad \to \stackrel{-1}{\phi}\big(\phi(M({\mathbb{Q}}_p))\big)/M({\mathbb{Q}}_p)\xleftarrow{\sim} F({\mathbb{A}}_f)/(F\cap M)({\mathbb{Q}}_p). \end{align}
The last group is a commutative group isomorphic to a subgroup of ![]() $({\mathbb {Z}}/(C))^\infty$ where
$({\mathbb {Z}}/(C))^\infty$ where ![]() $C=\lvert F(\overline {{\mathbb {Q}}}) \rvert$. Because
$C=\lvert F(\overline {{\mathbb {Q}}}) \rvert$. Because ![]() $U'$ is generated by
$U'$ is generated by ![]() $k$ elements, the size of the image of
$k$ elements, the size of the image of ![]() $U'$ is bounded by
$U'$ is bounded by ![]() $C^{k}$.
$C^{k}$.
We deduce
Proposition 6.7 For all ![]() $N\in {\mathbb {Z}}_{\geq 0}$ there exists
$N\in {\mathbb {Z}}_{\geq 0}$ there exists ![]() $k=k(N)$ such that for every prime
$k=k(N)$ such that for every prime ![]() $p$ and every subgroup
$p$ and every subgroup ![]() $U\leq GL(N,{\mathbb {F}}_p)$, there exist
$U\leq GL(N,{\mathbb {F}}_p)$, there exist ![]() $u_1,\ldots,u_{k}$ in
$u_1,\ldots,u_{k}$ in ![]() $U$ which generate
$U$ which generate ![]() $U$.
$U$.
Proof. We fix ![]() $N$. There exists
$N$. There exists ![]() $p(N)\in {\mathbb {Z}}_{\geq 0}$ such that
$p(N)\in {\mathbb {Z}}_{\geq 0}$ such that ![]() $p\geq p(N)$, so that Nori applies [Reference NoriNor87].
$p\geq p(N)$, so that Nori applies [Reference NoriNor87].
For ![]() $p\leq p(N)$ we have
$p\leq p(N)$ we have ![]() $\#U\leq \#GL(N,{\mathbb {F}}_p)\leq p(N)^{N^2}$ and we take
$\#U\leq \#GL(N,{\mathbb {F}}_p)\leq p(N)^{N^2}$ and we take ![]() $k(N)=p(N)^{N^2}$.
$k(N)=p(N)^{N^2}$.
We assume that ![]() $p\geq p(N)$ and apply Nori theory [Reference NoriNor87].
$p\geq p(N)$ and apply Nori theory [Reference NoriNor87].
According to Jordan theorem [Reference NoriNor87, Theorem C] there exist normal subgroups ![]() $U^+\leq U'\leq U$ with
$U^+\leq U'\leq U$ with ![]() $U^+$ generated by the unipotent elements of
$U^+$ generated by the unipotent elements of ![]() $U$, and
$U$, and ![]() $U'/U^+$ abelian of order prime to
$U'/U^+$ abelian of order prime to ![]() $p$, and
$p$, and ![]() $[U:U']\leq d(N)$, where
$[U:U']\leq d(N)$, where ![]() $d(N)$ is as in [Reference NoriNor87, Theorem C]. According to [Reference NoriNor87], there exists
$d(N)$ is as in [Reference NoriNor87, Theorem C]. According to [Reference NoriNor87], there exists ![]() $\tilde {U}\leq GL(N)_{{\mathbb {F}}_p}$ such that
$\tilde {U}\leq GL(N)_{{\mathbb {F}}_p}$ such that ![]() $\tilde {U}({\mathbb {F}}_p)^+=U^+$. Define
$\tilde {U}({\mathbb {F}}_p)^+=U^+$. Define ![]() $U''=\tilde {U}({\mathbb {F}}_p)\cap U$. Moreover, one knowsFootnote 15 that there exists an injective morphism
$U''=\tilde {U}({\mathbb {F}}_p)\cap U$. Moreover, one knowsFootnote 15 that there exists an injective morphism ![]() $U'/U''\hookrightarrow GL(N',{\mathbb {F}}_p)$, where
$U'/U''\hookrightarrow GL(N',{\mathbb {F}}_p)$, where ![]() $N'$ is bounded in terms of
$N'$ is bounded in terms of ![]() $N$.
$N$.
We will use the following remark. For every exact sequence ![]() $1\to K\to G \to Q\to 1$, if
$1\to K\to G \to Q\to 1$, if ![]() $K$ and
$K$ and ![]() $Q$ are generated by
$Q$ are generated by ![]() $k_N$ and
$k_N$ and ![]() $k_Q$ elements, then
$k_Q$ elements, then ![]() $G$ is generated by
$G$ is generated by ![]() $k_K+k_Q$ elements. Thus, in order to bound the size of a generating subset of
$k_K+k_Q$ elements. Thus, in order to bound the size of a generating subset of ![]() $G$, it suffices to do it for
$G$, it suffices to do it for ![]() $K$ and for
$K$ and for ![]() $Q$.
$Q$.
Using the remark, it will be enough to prove that ![]() $U/U'$,
$U/U'$, ![]() $U'/U''$,
$U'/U''$, ![]() $U''/U^+$ and
$U''/U^+$ and ![]() $U^+$ can be generated by
$U^+$ can be generated by ![]() $k_1(N),k_2(N),k_3(N),k_4(N)$ elements. Then the proposition will be satisfied with
$k_1(N),k_2(N),k_3(N),k_4(N)$ elements. Then the proposition will be satisfied with ![]() $k(N)=\max \{k_1(N)+k_2(N)+k_3(N)+k_4(N);p(N)^{N^2\!}\}$.
$k(N)=\max \{k_1(N)+k_2(N)+k_3(N)+k_4(N);p(N)^{N^2\!}\}$.
As ![]() $\#U/U' \leq d(N)$, we can take
$\#U/U' \leq d(N)$, we can take ![]() $k_1(N)=d(N)$.
$k_1(N)=d(N)$.
As ![]() $\tilde {U}$ is generated by unipotent subgroups, we can write
$\tilde {U}$ is generated by unipotent subgroups, we can write ![]() $\tilde {U}=\tilde {S}\cdot \tilde {N}$ where
$\tilde {U}=\tilde {S}\cdot \tilde {N}$ where ![]() $\tilde {S}$ is semisimple and
$\tilde {S}$ is semisimple and ![]() $\tilde {N}$ is the unipotent radical. According to [Reference NoriNor87, Remark 3.6, 3.6(v)], we have
$\tilde {N}$ is the unipotent radical. According to [Reference NoriNor87, Remark 3.6, 3.6(v)], we have ![]() $\tilde {S}({\mathbb {F}}_p)/\tilde {S}({\mathbb {F}}_p)^+\leq 2^N$. We deduce that
$\tilde {S}({\mathbb {F}}_p)/\tilde {S}({\mathbb {F}}_p)^+\leq 2^N$. We deduce that ![]() $\# U''/U^+\leq \# \tilde {U}({\mathbb {F}}_p)/\tilde {U}({\mathbb {F}}_p)^+=\# \tilde {S}({\mathbb {F}}_p)/\tilde {S}({\mathbb {F}}_p)^+ \leq 2^N$.
$\# U''/U^+\leq \# \tilde {U}({\mathbb {F}}_p)/\tilde {U}({\mathbb {F}}_p)^+=\# \tilde {S}({\mathbb {F}}_p)/\tilde {S}({\mathbb {F}}_p)^+ \leq 2^N$.
We can thus take ![]() $k_3(N)=2^N$.
$k_3(N)=2^N$.
The factor ![]() $U'/U''$ is isomorphic to an abelian subgroup of
$U'/U''$ is isomorphic to an abelian subgroup of ![]() $GL(N',{\mathbb {F}}_p)$ of order prime to
$GL(N',{\mathbb {F}}_p)$ of order prime to ![]() $p$. It is thus diagonalisable over some extension
$p$. It is thus diagonalisable over some extension ![]() ${\mathbb {F}}_q$. Because
${\mathbb {F}}_q$. Because ![]() ${{\mathbb {F}}_q}^\times$ is cyclic, every subgroup of
${{\mathbb {F}}_q}^\times$ is cyclic, every subgroup of ![]() $({{\mathbb {F}}_q}^\times )^{N'}$ is generated by at most
$({{\mathbb {F}}_q}^\times )^{N'}$ is generated by at most ![]() $N'$ elements.
$N'$ elements.
We can thus take ![]() $k_2(N)=N'$.
$k_2(N)=N'$.
Let ![]() $\tilde {U}\leq GL(N)_{{\mathbb {F}}_p}$ be the algebraic group associated to
$\tilde {U}\leq GL(N)_{{\mathbb {F}}_p}$ be the algebraic group associated to ![]() $U$ and let
$U$ and let ![]() $\tilde {\mathfrak {u}}\leq \mathfrak {gl}(N,{\mathbb {F}}_p)$ be its Lie algebra. By [Reference NoriNor87],
$\tilde {\mathfrak {u}}\leq \mathfrak {gl}(N,{\mathbb {F}}_p)$ be its Lie algebra. By [Reference NoriNor87], ![]() $\tilde {\mathfrak {u}}\leq \mathfrak {gl}(N,{\mathbb {F}}_p)$ is linearly generated by nilpotents. Let
$\tilde {\mathfrak {u}}\leq \mathfrak {gl}(N,{\mathbb {F}}_p)$ is linearly generated by nilpotents. Let ![]() $X_1,\ldots,X_d$, with
$X_1,\ldots,X_d$, with ![]() $d\leq N^2$ be a linear basis of nilpotent elements. Denote by
$d\leq N^2$ be a linear basis of nilpotent elements. Denote by ![]() $U'=\langle \exp (X_1),\ldots,\exp (X_d)\rangle$ the group generated by their exponentials, and consider the associated
$U'=\langle \exp (X_1),\ldots,\exp (X_d)\rangle$ the group generated by their exponentials, and consider the associated ![]() $\tilde {\mathfrak {u}}'\leq \tilde {\mathfrak {u}}$ and
$\tilde {\mathfrak {u}}'\leq \tilde {\mathfrak {u}}$ and ![]() $\tilde {U}'\leq \tilde {U}$. We have
$\tilde {U}'\leq \tilde {U}$. We have ![]() $X_1,\ldots,X_d\in \tilde {\mathfrak {u}}'$. Thus,
$X_1,\ldots,X_d\in \tilde {\mathfrak {u}}'$. Thus, ![]() $\tilde {\mathfrak {u}}'=\tilde {\mathfrak {u}}$ and
$\tilde {\mathfrak {u}}'=\tilde {\mathfrak {u}}$ and ![]() $\tilde {U}'=\tilde {U}$. From [Reference NoriNor87, Theorem B], we get
$\tilde {U}'=\tilde {U}$. From [Reference NoriNor87, Theorem B], we get ![]() $U=U^+=\tilde {U}({\mathbb {F}}_p)^+=\tilde {U}'({\mathbb {F}}_p)^+=U'^+=U'$. Thus,
$U=U^+=\tilde {U}({\mathbb {F}}_p)^+=\tilde {U}'({\mathbb {F}}_p)^+=U'^+=U'$. Thus, ![]() $U$ is generated by at most
$U$ is generated by at most ![]() $N^2$ elements
$N^2$ elements ![]() $\exp (X_1),\ldots,\exp (X_d)$.
$\exp (X_1),\ldots,\exp (X_d)$.
We can thus take ![]() $k_4(N)=N^2$.
$k_4(N)=N^2$.
We used the following.
Lemma 6.8 Let ![]() $M\leq GL(N)$ be an algebraic subgroup defined over
$M\leq GL(N)$ be an algebraic subgroup defined over ![]() ${\mathbb {Q}}_p$ and let
${\mathbb {Q}}_p$ and let ![]() $\mathfrak {m}\leq \mathfrak {gl}(N,{\mathbb {Q}}_p)$ be its Lie algebra.
$\mathfrak {m}\leq \mathfrak {gl}(N,{\mathbb {Q}}_p)$ be its Lie algebra.
(i) Let
 $V\leq GL(N,{\mathbb {Z}}_p)$ a compact subgroup. Then
$V\leq GL(N,{\mathbb {Z}}_p)$ a compact subgroup. Then  $V$ is topologically finitely generated.
$V$ is topologically finitely generated.(ii) Then
 $V':=\exp (\mathfrak {m}\cap 2p\mathfrak {gl}(N,{\mathbb {Z}}_p))$ is topologically generated by at most
$V':=\exp (\mathfrak {m}\cap 2p\mathfrak {gl}(N,{\mathbb {Z}}_p))$ is topologically generated by at most  $N^2$ elements if
$N^2$ elements if  $p$ is large enough.
$p$ is large enough.(iii) Let
 $M({\mathbb {Z}}_p):=M({\mathbb {Q}}_p)\cap GL(N,{\mathbb {Z}}_p)$ and
$M({\mathbb {Z}}_p):=M({\mathbb {Q}}_p)\cap GL(N,{\mathbb {Z}}_p)$ and  $V\leq M({\mathbb {Z}}_p)$ an open subgroup such that
$V\leq M({\mathbb {Z}}_p)$ an open subgroup such that  $C:=[M({\mathbb {Z}}_p):V]\in {\mathbb {Z}}_{\geq 1}$. Then for
$C:=[M({\mathbb {Z}}_p):V]\in {\mathbb {Z}}_{\geq 1}$. Then for  $p>C$, we have
$p>C$, we have
 \[ V'\leq V. \]
\[ V'\leq V. \]
Proof. The first assertion is [Reference SerreSer64, Proposition 2].
Let ![]() $G=\exp (2p\mathfrak {gl}(N,{\mathbb {Z}}_p))= 1+2p\mathfrak {gl}(N,{\mathbb {Z}}_p)$ and
$G=\exp (2p\mathfrak {gl}(N,{\mathbb {Z}}_p))= 1+2p\mathfrak {gl}(N,{\mathbb {Z}}_p)$ and ![]() $H=V'\leq G$. According to [Reference Dixon, du Sautoy, Mann and SegalDSMS99, Theorem 5.2] the pro-
$H=V'\leq G$. According to [Reference Dixon, du Sautoy, Mann and SegalDSMS99, Theorem 5.2] the pro-![]() $p$ group is powerful and
$p$ group is powerful and ![]() $d(G)=N^2$, where
$d(G)=N^2$, where ![]() $d(G)$ is the minimal cardinality of a set of generators for
$d(G)$ is the minimal cardinality of a set of generators for ![]() $G$ as in [Reference Dixon, du Sautoy, Mann and SegalDSMS99, p. 41]. We can, thus, apply [Reference Dixon, du Sautoy, Mann and SegalDSMS99, Theorem 2.9]. This proves the second assertion.
$G$ as in [Reference Dixon, du Sautoy, Mann and SegalDSMS99, p. 41]. We can, thus, apply [Reference Dixon, du Sautoy, Mann and SegalDSMS99, Theorem 2.9]. This proves the second assertion.
As ![]() $G$ is a pro-
$G$ is a pro-![]() $p$ group, by [Reference Platonov and RapinchukPR94, Lemma 4.8, p. 138],
$p$ group, by [Reference Platonov and RapinchukPR94, Lemma 4.8, p. 138], ![]() $V'$ is a pro-
$V'$ is a pro-![]() $p$ group. We also have
$p$ group. We also have
Assume ![]() $p>C$ and assume, by contradiction, that there exists
$p>C$ and assume, by contradiction, that there exists ![]() $w\in V'\smallsetminus V$. We denote by
$w\in V'\smallsetminus V$. We denote by ![]() $w^{\mathbb {Z}}$ the subgroup generated by
$w^{\mathbb {Z}}$ the subgroup generated by ![]() $w$. Then
$w$. Then ![]() $c:=[w^{\mathbb {Z}}:w^{\mathbb {Z}}\cap V]\neq 1$ and
$c:=[w^{\mathbb {Z}}:w^{\mathbb {Z}}\cap V]\neq 1$ and ![]() $c\leq C$. But
$c\leq C$. But ![]() $c$ is a power of
$c$ is a power of ![]() $p$ because
$p$ because ![]() $V'$ is a pro-
$V'$ is a pro-![]() $p$ group: thus,
$p$ group: thus, ![]() $c\geq p$. We deduce that
$c\geq p$. We deduce that ![]() $C\geq c\geq p$. This contradicts our assumptions.
$C\geq c\geq p$. This contradicts our assumptions.
We prove assertion (iii) of Lemma 6.5. We will make use of Goursat's lemma.
Proof. As ![]() $M$ is reductive, the map
$M$ is reductive, the map ![]() $(ad_M,ab_M):M\to M':=M^{\rm ad}\times M^{\rm ab}$ is an isogeny. From assertion (ii) of Lemma 6.5 it follows that it is enough to prove that the image
$(ad_M,ab_M):M\to M':=M^{\rm ad}\times M^{\rm ab}$ is an isogeny. From assertion (ii) of Lemma 6.5 it follows that it is enough to prove that the image ![]() $V$ of
$V$ of ![]() $U$ in
$U$ in ![]() $M'({\mathbb {A}}_f)$ is MT in
$M'({\mathbb {A}}_f)$ is MT in ![]() $M'$. We may thus assume
$M'$. We may thus assume ![]() $M=M^{\rm ad}\times M^{\rm ab}$.
$M=M^{\rm ad}\times M^{\rm ab}$.
Using Lemma 6.2 we may assume ![]() $U=\prod _p U_p$. Let
$U=\prod _p U_p$. Let
be a maximal compact subgroup containing ![]() $U$.
$U$.
By assumption, there is an upper bound ![]() $C\in {\mathbb {Z}}_{\geq 1}$ for
$C\in {\mathbb {Z}}_{\geq 1}$ for ![]() $[K_{M^{\rm ab},p}:ab_M(U_p)]$ and
$[K_{M^{\rm ab},p}:ab_M(U_p)]$ and ![]() $[K_{M^{\rm ad},p}:ad_M(U_p)]$, independent of
$[K_{M^{\rm ad},p}:ad_M(U_p)]$, independent of ![]() $p$.
$p$.
Let ![]() $H_1=ad_M(U_p)$ and
$H_1=ad_M(U_p)$ and ![]() $H_2=ab_M(U_p)$ and
$H_2=ab_M(U_p)$ and ![]() $\Gamma =(ad_M,ab_M)(U_p)\leq H_1\times H_2$. Let
$\Gamma =(ad_M,ab_M)(U_p)\leq H_1\times H_2$. Let ![]() $N_1=\Gamma \cap H_1$ and
$N_1=\Gamma \cap H_1$ and ![]() $N_2=\Gamma \cap H_2$. By Goursat's lemma,
$N_2=\Gamma \cap H_2$. By Goursat's lemma, ![]() $N_1$ and
$N_1$ and ![]() $N_2$ are normal subgroups in
$N_2$ are normal subgroups in ![]() $H_1$ and
$H_1$ and ![]() $H_2$ and there is an isomorphism (whose graph is
$H_2$ and there is an isomorphism (whose graph is ![]() $\Gamma /(N_1\times N_2)$)
$\Gamma /(N_1\times N_2)$)
Because ![]() $H_2$ is abelian,
$H_2$ is abelian, ![]() $N_1$ contains the derived subgroup
$N_1$ contains the derived subgroup ![]() $[H_1,H_1]$.
$[H_1,H_1]$.
By the first part of Lemma 6.9, ![]() $[H_1:N_1]$ is finite for every prime
$[H_1:N_1]$ is finite for every prime ![]() $p$, and by the second part of Lemma 6.9,
$p$, and by the second part of Lemma 6.9, ![]() $[H_1:N_1]$ is bounded by
$[H_1:N_1]$ is bounded by ![]() $C(M^{\rm ad})$ for almost every prime
$C(M^{\rm ad})$ for almost every prime ![]() $p$.
$p$.
As a result there exists ![]() $C'\in {\mathbb {Z}}_{\geq 1}$ such that
$C'\in {\mathbb {Z}}_{\geq 1}$ such that ![]() $[H_1:N_1]\leq C'$ for every prime
$[H_1:N_1]\leq C'$ for every prime ![]() $p$. Using (54), we also have
$p$. Using (54), we also have ![]() $[H_2:N_2]\leq C'$ for every prime
$[H_2:N_2]\leq C'$ for every prime ![]() $p$.
$p$.
Recall that ![]() $N_1\times N_2\leq \Gamma$. It follows
$N_1\times N_2\leq \Gamma$. It follows
By the definition of ![]() $C$,
$C$,
We deduce
The bound is independent of ![]() $p$, which concludes.
$p$, which concludes.
Lemma 6.9 Let ![]() $G$ be a semisimple algebraic group over
$G$ be a semisimple algebraic group over ![]() ${\mathbb {Q}}$, and for every prime
${\mathbb {Q}}$, and for every prime ![]() $p$, let
$p$, let ![]() $U_p,K_p\leq G({\mathbb {Q}}_p)$ be compact open subgroups such that
$U_p,K_p\leq G({\mathbb {Q}}_p)$ be compact open subgroups such that ![]() $K=\prod _p K_p\leq G({\mathbb {A}}_f)$ is open. Let
$K=\prod _p K_p\leq G({\mathbb {A}}_f)$ is open. Let ![]() $[U_p,U_p]$ be the subgroup generated by commutators.
$[U_p,U_p]$ be the subgroup generated by commutators.
(i) For every prime
 $p$, the quotient
$p$, the quotient  $U_p/[U_p,U_p]$ is finite.
$U_p/[U_p,U_p]$ is finite.(ii) There exists
 $C(G)\in {\mathbb {Z}}_{\geq 1}$ such that, for almost all
$C(G)\in {\mathbb {Z}}_{\geq 1}$ such that, for almost all  $p$, if
$p$, if  $[K_p:U_p\cap K_p]< p$ then
$[K_p:U_p\cap K_p]< p$ then  $U_p/[U_p,U_p]< C(G)$.
$U_p/[U_p,U_p]< C(G)$.
Proof. The first assertion follows from the fact that ![]() $[U_p,U_p]$ is open, because
$[U_p,U_p]$ is open, because ![]() $G$ is semisimple.
$G$ is semisimple.
We prove the second assertion. We may replace ![]() $U_p$ by
$U_p$ by ![]() $K_p\cap U_p$ and assume
$K_p\cap U_p$ and assume ![]() $U_p=K_p\cap U_p\leq K_p$. Thus,
$U_p=K_p\cap U_p\leq K_p$. Thus, ![]() $[K_p:K_p\cap U_p]=[K_p:U_p]< p$.
$[K_p:K_p\cap U_p]=[K_p:U_p]< p$.
Let us identify ![]() $G$ with its image by a faithful linear representation
$G$ with its image by a faithful linear representation ![]() $G\to GL(N)$. For
$G\to GL(N)$. For ![]() $p$ large enough, we have
$p$ large enough, we have ![]() $K_p= G({\mathbb {Z}}_p):=G({\mathbb {Q}}_p)\cap GL(N,{\mathbb {Z}}_p)$.
$K_p= G({\mathbb {Z}}_p):=G({\mathbb {Q}}_p)\cap GL(N,{\mathbb {Z}}_p)$.
Let ![]() $G({\mathbb {Z}}_p)^+$ and
$G({\mathbb {Z}}_p)^+$ and ![]() $G({\mathbb {F}}_p)^+$ be as in Lemma 6.10 below.
$G({\mathbb {F}}_p)^+$ be as in Lemma 6.10 below.
Then ![]() $U_p\cap G({\mathbb {Z}}_p)^+$ is an open subgroup of
$U_p\cap G({\mathbb {Z}}_p)^+$ is an open subgroup of ![]() $G({\mathbb {Z}}_p)^+$ and,
$G({\mathbb {Z}}_p)^+$ and,
(Recall the assumption ![]() $[K_p:U_p]< p$.)
$[K_p:U_p]< p$.)
As ![]() $G({\mathbb {Z}}_p)^+$ is generated by pro-
$G({\mathbb {Z}}_p)^+$ is generated by pro-![]() $p$-groups, we have, for every subgroup
$p$-groups, we have, for every subgroup ![]() $L\leq G({\mathbb {Z}}_p)^+$,
$L\leq G({\mathbb {Z}}_p)^+$,
Therefore, with ![]() $L=U_p$,
$L=U_p$,
At the level of derived subgroups, we have
We deduce
We note that ![]() $G({\mathbb {Z}}_p)^+\leq G({\mathbb {Z}}_p)$ is an open subgroup of index prime to
$G({\mathbb {Z}}_p)^+\leq G({\mathbb {Z}}_p)$ is an open subgroup of index prime to ![]() $p$. It follows that the image of
$p$. It follows that the image of ![]() $G({\mathbb {Z}}_p)^+$ in
$G({\mathbb {Z}}_p)^+$ in ![]() $G({\mathbb {F}}_p)$ contains
$G({\mathbb {F}}_p)$ contains ![]() $G({\mathbb {F}}_p)^+$. Thus,
$G({\mathbb {F}}_p)^+$. Thus,
We have, by [Reference NoriNor87, p. 270],
For ![]() $p$ large enough we have:
$p$ large enough we have:
–
 $G({\mathbb {F}}_p)=\tilde {G}({\mathbb {F}}_p)$ for a connected semisimple
$G({\mathbb {F}}_p)=\tilde {G}({\mathbb {F}}_p)$ for a connected semisimple  ${\mathbb {F}}_p$-algebraic subgroup
${\mathbb {F}}_p$-algebraic subgroup  $\tilde {G}\leq GL(N)_{{\mathbb {F}}_p}$;
$\tilde {G}\leq GL(N)_{{\mathbb {F}}_p}$;–
 $[\tilde {G}({\mathbb {F}}_p)^+,\tilde {G}({\mathbb {F}}_p)^+]=[\tilde {G},\tilde {G}]({\mathbb {F}}_p)^+=\tilde {G}({\mathbb {F}}_p)^+$, using Lemma 6.11.
$[\tilde {G}({\mathbb {F}}_p)^+,\tilde {G}({\mathbb {F}}_p)^+]=[\tilde {G},\tilde {G}]({\mathbb {F}}_p)^+=\tilde {G}({\mathbb {F}}_p)^+$, using Lemma 6.11.
Thus, ![]() $[G({\mathbb {Z}}_p)^+,G({\mathbb {Z}}_p)^+]$ maps surjectively onto
$[G({\mathbb {Z}}_p)^+,G({\mathbb {Z}}_p)^+]$ maps surjectively onto
We apply Lemma 6.10 to ![]() $H=[G({\mathbb {Z}}_p)^+,G({\mathbb {Z}}_p)^+]$. We deduce
$H=[G({\mathbb {Z}}_p)^+,G({\mathbb {Z}}_p)^+]$. We deduce
This implies
The second assertion of Lemma 6.9 follows from (55) and (56).
Lemma 6.10 [Reference Cadoret and KretCK16, Fact 2.4 and its proof]
Let ![]() $G\leq GL(N)_{{\mathbb {Q}}}$ be a connected semisimple algebraic subgroup. For every prime
$G\leq GL(N)_{{\mathbb {Q}}}$ be a connected semisimple algebraic subgroup. For every prime ![]() $p$, define
$p$, define ![]() $G({\mathbb {Z}}_p):=G({\mathbb {Q}}_p)\cap GL(N,{\mathbb {Z}}_p)$ and denote by
$G({\mathbb {Z}}_p):=G({\mathbb {Q}}_p)\cap GL(N,{\mathbb {Z}}_p)$ and denote by ![]() $G({\mathbb {F}}_p)$ the image of
$G({\mathbb {F}}_p)$ the image of ![]() $G({\mathbb {Z}}_p)$ in
$G({\mathbb {Z}}_p)$ in ![]() $GL(N,{\mathbb {F}}_p)$. We denote by
$GL(N,{\mathbb {F}}_p)$. We denote by ![]() $G({\mathbb {F}}_p)^+\leq G({\mathbb {F}}_p)$ and
$G({\mathbb {F}}_p)^+\leq G({\mathbb {F}}_p)$ and ![]() $G({\mathbb {Z}}_p)^+\leq G({\mathbb {Z}}_p)$ the subgroups generated by
$G({\mathbb {Z}}_p)^+\leq G({\mathbb {Z}}_p)$ the subgroups generated by ![]() $p$-Sylow subgroups, respectively, pro-
$p$-Sylow subgroups, respectively, pro-![]() $p$-Sylow.
$p$-Sylow.
Then, for ![]() $p$ large enough: if
$p$ large enough: if ![]() $H\leq G({\mathbb {Z}}_p)^+$ maps surjectively onto
$H\leq G({\mathbb {Z}}_p)^+$ maps surjectively onto ![]() $G({\mathbb {F}}_p)^+$, then
$G({\mathbb {F}}_p)^+$, then ![]() $H=G({\mathbb {Z}}_p)$.
$H=G({\mathbb {Z}}_p)$.
We used the following in the proof of Lemma 6.9.
Lemma 6.11 For every ![]() $n\in {\mathbb {Z}}_{\geq 0}$, there exists
$n\in {\mathbb {Z}}_{\geq 0}$, there exists ![]() $c(n)$ such that the following holds. Let
$c(n)$ such that the following holds. Let ![]() $p\geq c(n)$ be a prime, and let
$p\geq c(n)$ be a prime, and let ![]() $G\leq GL(n)$ be a semisimple algebraic group over
$G\leq GL(n)$ be a semisimple algebraic group over ![]() ${\mathbb {F}}_p$.
${\mathbb {F}}_p$.
Then ![]() $[G({\mathbb {F}}_p)^+,G({\mathbb {F}}_p)^+]=G({\mathbb {F}}_p)^+$.
$[G({\mathbb {F}}_p)^+,G({\mathbb {F}}_p)^+]=G({\mathbb {F}}_p)^+$.
Proof. Let ![]() $\pi :G^{\rm sc}\to G$ be the simply connected cover. According to [Reference Malle and TestermanMT11, 24.15], we have
$\pi :G^{\rm sc}\to G$ be the simply connected cover. According to [Reference Malle and TestermanMT11, 24.15], we have ![]() $G^{\rm sc}({\mathbb {F}}_p)^+=G^{\rm sc}({\mathbb {F}}_p)$.
$G^{\rm sc}({\mathbb {F}}_p)^+=G^{\rm sc}({\mathbb {F}}_p)$.
It follows that ![]() $\pi (G^{\rm sc}({\mathbb {F}}_p))\leq G({\mathbb {F}}_p)^+$. Since
$\pi (G^{\rm sc}({\mathbb {F}}_p))\leq G({\mathbb {F}}_p)^+$. Since ![]() $G({\mathbb {F}}_p)^+$ is generated by elements of order a power of
$G({\mathbb {F}}_p)^+$ is generated by elements of order a power of ![]() $p$, we have the following alternative:
$p$, we have the following alternative:
– either
 $\pi (G^{\rm sc}({\mathbb {F}}_p))= G({\mathbb {F}}_p)^+$;
$\pi (G^{\rm sc}({\mathbb {F}}_p))= G({\mathbb {F}}_p)^+$;– or
 $\# G({\mathbb {F}}_p)^+/\pi (G^{\rm sc}({\mathbb {F}}_p))\geq p$.
$\# G({\mathbb {F}}_p)^+/\pi (G^{\rm sc}({\mathbb {F}}_p))\geq p$.
Let ![]() $Z=\ker (\pi : G^{\rm sc}(\overline {{\mathbb {F}}_p})\to G(\overline {{\mathbb {F}}_p}))$.
$Z=\ker (\pi : G^{\rm sc}(\overline {{\mathbb {F}}_p})\to G(\overline {{\mathbb {F}}_p}))$.
By [Reference Malle and TestermanMT11, 24.21], we have ![]() $\# G({\mathbb {F}}_p)^+/\pi (G^{\rm sc}({\mathbb {F}}_p))\leq \#Z$.
$\# G({\mathbb {F}}_p)^+/\pi (G^{\rm sc}({\mathbb {F}}_p))\leq \#Z$.
On the other hand, there exists an integer ![]() $c(n)$ (depending only on
$c(n)$ (depending only on ![]() $n$) such that we have
$n$) such that we have ![]() $\# Z\leq c(n)$. Thus, for
$\# Z\leq c(n)$. Thus, for ![]() $p>c(n)$, the second case of the alternative does not happen.
$p>c(n)$, the second case of the alternative does not happen.
By [Reference Malle and TestermanMT11, 24.17], for ![]() $p\geq 4$, the group
$p\geq 4$, the group ![]() $G^{\rm sc}(\overline {{\mathbb {F}}_p})$ is perfect. It implies that its quotient
$G^{\rm sc}(\overline {{\mathbb {F}}_p})$ is perfect. It implies that its quotient ![]() $\pi (G^{\rm sc}({\mathbb {F}}_p))= G({\mathbb {F}}_p)^+$ is perfect, namely, that
$\pi (G^{\rm sc}({\mathbb {F}}_p))= G({\mathbb {F}}_p)^+$ is perfect, namely, that ![]() $[G({\mathbb {F}}_p)^+,G({\mathbb {F}}_p)^+]=G({\mathbb {F}}_p)^+$.
$[G({\mathbb {F}}_p)^+,G({\mathbb {F}}_p)^+]=G({\mathbb {F}}_p)^+$.
6.4 MT hypothesis for Images of Galois representations
We use the notation of Definition 6.3. We assume furthermore that ![]() $E$ is of finite type over
$E$ is of finite type over ![]() ${\mathbb {Q}}$. In this case, we have the following.
${\mathbb {Q}}$. In this case, we have the following.
Lemma 6.12 If ![]() $x_0$ is a special point (i.e.
$x_0$ is a special point (i.e. ![]() $M=M^{\rm ab}$), then
$M=M^{\rm ab}$), then ![]() $x_0$ satisfies the MT hypothesis.
$x_0$ satisfies the MT hypothesis.
The Galois representation ![]() $Gal(\overline {E}/E)\to M^{\rm ab}({\mathbb {A}}_f)$ is prescribed by Deligne–Shimura reciprocity law, which is part of the definition of a canonical model [Reference DeligneDel79, 2.2.5]. In this case, we know that
$Gal(\overline {E}/E)\to M^{\rm ab}({\mathbb {A}}_f)$ is prescribed by Deligne–Shimura reciprocity law, which is part of the definition of a canonical model [Reference DeligneDel79, 2.2.5]. In this case, we know that ![]() $M=M^{\rm ab}$ is the Zariski closure of the image of
$M=M^{\rm ab}$ is the Zariski closure of the image of ![]() $x_0$. It follows that the morphism [Reference DeligneDel79, 2.2.2.1] is an epimorphism, and we can apply Theorem 6.6.Footnote 16
$x_0$. It follows that the morphism [Reference DeligneDel79, 2.2.2.1] is an epimorphism, and we can apply Theorem 6.6.Footnote 16
Using Lemmas 6.12 and of 6.5(iii) we have the following.
Lemma 6.13 The point ![]() $x_0$ satisfies the MT hypothesis if and only if
$x_0$ satisfies the MT hypothesis if and only if ![]() $ad_M(x_0)$ satisfies the MT hypothesis.
$ad_M(x_0)$ satisfies the MT hypothesis.
The following is not needed but can help relate our MT hypothesis to other notions found in literature.
Theorem 6.14 Assume ![]() $M$ is a semisimple and simply connected algebraic group over
$M$ is a semisimple and simply connected algebraic group over ![]() ${\mathbb {Q}}$. Then a compact subgroup
${\mathbb {Q}}$. Then a compact subgroup ![]() $U\leq M({\mathbb {A}}_f)$ is MT in
$U\leq M({\mathbb {A}}_f)$ is MT in ![]() $M$ if and only if it is an open subgroup.
$M$ if and only if it is an open subgroup.
Theorem 6.14 is a consequence of the following.
Lemma 6.15 Let ![]() $M\leq GL(n)_{{\mathbb {Q}}}$ be a simply connected semisimple
$M\leq GL(n)_{{\mathbb {Q}}}$ be a simply connected semisimple ![]() ${\mathbb {Q}}$-algebraic subgroup, and, for every prime
${\mathbb {Q}}$-algebraic subgroup, and, for every prime ![]() $p$, define
$p$, define ![]() $M({\mathbb {Z}}_p):=M({\mathbb {Q}}_p)\cap GL(n,{\mathbb {Z}}_p)$.
$M({\mathbb {Z}}_p):=M({\mathbb {Q}}_p)\cap GL(n,{\mathbb {Z}}_p)$.
There exists ![]() $C$ such that for every prime
$C$ such that for every prime ![]() $p\geq C$, every
$p\geq C$, every ![]() $U\leq M({\mathbb {Z}}_p)$ satisfies
$U\leq M({\mathbb {Z}}_p)$ satisfies
Proof. This is a consequence of the following claim: for ![]() $p\gg 0$, the group
$p\gg 0$, the group ![]() $M({\mathbb {Z}}_p)$ is generated by topologically
$M({\mathbb {Z}}_p)$ is generated by topologically ![]() $p$-nilpotent elements.
$p$-nilpotent elements.
Let us prove the claim. For every prime ![]() $p$, every element in the kernel of the morphisms
$p$, every element in the kernel of the morphisms ![]() $red_p:M({\mathbb {Z}}_p)\to GL(n,{\mathbb {F}}_p)$ belongs to
$red_p:M({\mathbb {Z}}_p)\to GL(n,{\mathbb {F}}_p)$ belongs to ![]() $1+p\mathfrak {gl(n,{\mathbb {Z}}_p)}$ and is topologically
$1+p\mathfrak {gl(n,{\mathbb {Z}}_p)}$ and is topologically ![]() $p$-nilpotent. It will be enough to prove that
$p$-nilpotent. It will be enough to prove that ![]() $red_p(M({\mathbb {Z}}_p))$ is generated by elements of order power of
$red_p(M({\mathbb {Z}}_p))$ is generated by elements of order power of ![]() $p$. For
$p$. For ![]() $p\gg 0$, the group
$p\gg 0$, the group ![]() $M({\mathbb {Z}}_p)$ is hyperspecial and the model of
$M({\mathbb {Z}}_p)$ is hyperspecial and the model of ![]() $M$ induced by
$M$ induced by ![]() $GL(n)_{{\mathbb {Z}}}$ is smooth over
$GL(n)_{{\mathbb {Z}}}$ is smooth over ![]() ${\mathbb {Z}}_p$ with semisimple fibre
${\mathbb {Z}}_p$ with semisimple fibre ![]() $M_{{\mathbb {F}}_p}$. This implies that the map
$M_{{\mathbb {F}}_p}$. This implies that the map ![]() $M({\mathbb {Z}}_p)\to M_{{\mathbb {F}}_p}({\mathbb {F}}_p)$ is surjective. For
$M({\mathbb {Z}}_p)\to M_{{\mathbb {F}}_p}({\mathbb {F}}_p)$ is surjective. For ![]() $p\gg 0$ the algebraic group
$p\gg 0$ the algebraic group ![]() $M_{{\mathbb {F}}_p}$ is semisimple and simply connected.Footnote 17 By [Reference Malle and TestermanMT11, 24.15] we have
$M_{{\mathbb {F}}_p}$ is semisimple and simply connected.Footnote 17 By [Reference Malle and TestermanMT11, 24.15] we have ![]() $M({\mathbb {F}}_p)=M({\mathbb {F}}_p)^+$. This proves the claim.
$M({\mathbb {F}}_p)=M({\mathbb {F}}_p)^+$. This proves the claim.
This relies on strong approximation, Hasse principle, and Kneser–Tits properties for ![]() $M$. See [Reference DeligneDel71] for related discussions.
$M$. See [Reference DeligneDel71] for related discussions.
6.4.1
For moduli spaces of abelian varieties or, more generally, for Shimura varieties of abelian type, a Galois representation associated to a point ![]() $x_0\in X$ can be deduced from the Galois representation on the Tate module of an abelian variety.
$x_0\in X$ can be deduced from the Galois representation on the Tate module of an abelian variety.
We have the following.
Theorem 6.16 [Reference Cadoret and MoonenCM20, Theorem A(i)] and [Reference Hindry and RatazziHR16, Theorem 10.1]
Let ![]() $S$ be a Shimura variety of Hodge type, let
$S$ be a Shimura variety of Hodge type, let ![]() $s\in S$ be a point.
$s\in S$ be a point.
If the abelian variety ![]() $A$ associated to
$A$ associated to ![]() $s$ satisfies the classical Mumford–Tate conjecture at some prime
$s$ satisfies the classical Mumford–Tate conjecture at some prime ![]() $\ell$, then
$\ell$, then ![]() $s$ satisfies the weakly adelic Mumford–Tate hypothesis.
$s$ satisfies the weakly adelic Mumford–Tate hypothesis.
Using Lemma 6.13 we can deduce the following.
Theorem 6.17 Let ![]() $S$ be a Shimura variety of abelian type, let
$S$ be a Shimura variety of abelian type, let ![]() $s\in S$ be a point.
$s\in S$ be a point.
If ![]() $s$ satisfies the Mumford–Tate conjecture at some prime
$s$ satisfies the Mumford–Tate conjecture at some prime ![]() $\ell$ in the sense of [Reference Ullmo and YafaevUY13], then
$\ell$ in the sense of [Reference Ullmo and YafaevUY13], then ![]() $s$ satisfies the weakly adelic Mumford–Tate hypothesis.
$s$ satisfies the weakly adelic Mumford–Tate hypothesis.
6.4.2
As observed in [Reference BaldiBal20], the combination of a theorem of Deligne and André and with a theorem of Weisfeiler [Reference Matthews, Vaserstein and WeisfeilerMVW84] and Nori [Reference NoriNor87] produces, in any Shimura variety, many examples of (non-algebraic) points for which the MT hypothesis is satisfied. With our terminology it is stated as follows.
Theorem 6.18 [Reference BaldiBal20, Theorem 1.2]
Let ![]() $M$ be the Mumford–Tate group of a point
$M$ be the Mumford–Tate group of a point ![]() $x_0\in X$ for a Shimura datum
$x_0\in X$ for a Shimura datum ![]() $(G,X)$. We decompose the adjoint datum
$(G,X)$. We decompose the adjoint datum ![]() $(M^{\rm ad},X_{M^{\rm ad}})$ of
$(M^{\rm ad},X_{M^{\rm ad}})$ of ![]() $(M,X_M):=(M,M({\mathbb {R}})\cdot x_0)$ as a product
$(M,X_M):=(M,M({\mathbb {R}})\cdot x_0)$ as a product
with respect to the ![]() ${\mathbb {Q}}$-simple factors
${\mathbb {Q}}$-simple factors ![]() $M_i$ of
$M_i$ of ![]() $M^{\rm ad}$.
$M^{\rm ad}$.
Assume that for some compact open subgroups ![]() $K_i\leq M_i({\mathbb {A}}_f)$
$K_i\leq M_i({\mathbb {A}}_f)$
Then ![]() $x_0$ satisfies the MT hypothesis.
$x_0$ satisfies the MT hypothesis.
7. Proof of the main result
In this section we prove the Theorem 1.2, following the strategy outlined in § 1.4. We then give in § 7.3 a variant of the Pila–Wilkie theorem.
7.1 Reduction steps
We put ourselves in the situation of Theorem 1.2 and Conjecture 1.1.
Let ![]() $Z$ be an irreducible component of
$Z$ be an irreducible component of ![]() $\overline {\Sigma }^{\rm Zar}$. The aim is to prove that
$\overline {\Sigma }^{\rm Zar}$. The aim is to prove that ![]() $Z$ is weakly special. We may replace
$Z$ is weakly special. We may replace ![]() $\Sigma$ by
$\Sigma$ by ![]() $\mathcal {H}(x_0)\cap Z$.
$\mathcal {H}(x_0)\cap Z$.
7.1.1 Reduction to the Hodge generic case
We will reduce the theorem to the case where ![]() $Z$ is Hodge generic in
$Z$ is Hodge generic in ![]() $Sh_K(G,X)$. For convenience, we will assume that
$Sh_K(G,X)$. For convenience, we will assume that ![]() $s_0=[x_0,1]\in Z$. We choose a Hodge generic point
$s_0=[x_0,1]\in Z$. We choose a Hodge generic point ![]() $z$ in
$z$ in ![]() $Z$. One knows that one can choose a lift
$Z$. One knows that one can choose a lift ![]() $\tilde {z}$ of
$\tilde {z}$ of ![]() $z$ in
$z$ in ![]() $X$ such that the Mumford–Tate group
$X$ such that the Mumford–Tate group ![]() $G'$ of
$G'$ of ![]() $\tilde {z}$ contains
$\tilde {z}$ contains ![]() $M$. We write
$M$. We write ![]() $X'=G'({\mathbb {R}})\cdot \tilde {z}$. We have a Shimura morphism
$X'=G'({\mathbb {R}})\cdot \tilde {z}$. We have a Shimura morphism
(The smallest special subvariety of ![]() $Sh_K(G,X)$ containing
$Sh_K(G,X)$ containing ![]() $Z$ is the image of one component of
$Z$ is the image of one component of ![]() $Sh_{K\cap G'({\mathbb {A}}_f)}(G',X')$.) Let
$Sh_{K\cap G'({\mathbb {A}}_f)}(G',X')$.) Let ![]() $Z'$ be the inverse image of
$Z'$ be the inverse image of ![]() $Z$ by
$Z$ by ![]() $\Psi$. It is known that
$\Psi$. It is known that ![]() $Z$ is weakly special if and only if any component of
$Z$ is weakly special if and only if any component of ![]() $Z'$ is weakly special.
$Z'$ is weakly special.
In the notation of Proposition 2.6, we have
Because ![]() $Sh_{K\cap G'({\mathbb {A}}_f)}(G',X')\to \Psi (Sh_{K\cap G'({\mathbb {A}}_f)}(G',X'))$ is flat, and because
$Sh_{K\cap G'({\mathbb {A}}_f)}(G',X')\to \Psi (Sh_{K\cap G'({\mathbb {A}}_f)}(G',X'))$ is flat, and because ![]() $Z$ is in the image of
$Z$ is in the image of ![]() $\Psi$, we deduce that
$\Psi$, we deduce that ![]() $\Sigma '$ is dense in
$\Sigma '$ is dense in ![]() $Z'$ and, hence, dense in every component of
$Z'$ and, hence, dense in every component of ![]() $Z'$.
$Z'$.
Thus, in proving the conclusion of the theorem we may replace ![]() $Z$ by a component of
$Z$ by a component of ![]() $Z'$, and
$Z'$, and ![]() $(G,X)$ by
$(G,X)$ by ![]() $(G',X')$, and
$(G',X')$, and ![]() $K$ by
$K$ by ![]() $K\cap G'({\mathbb {A}}_f)$.
$K\cap G'({\mathbb {A}}_f)$.
On the other hand, the Mumford–Tate hypothesis depends only on ![]() $M$, and thus is insensitive to such substitutions.
$M$, and thus is insensitive to such substitutions.
In other words, we can, and will, assume that ![]() $Z$ is Hodge generic in
$Z$ is Hodge generic in ![]() $Sh_K(G,X)$.
$Sh_K(G,X)$.
7.1.2 Reduction to the adjoint datum
We will reduce the theorem to the case where ![]() $G=G^{\rm ad}$ is of adjoint type. Here we use geometric Hecke orbits.
$G=G^{\rm ad}$ is of adjoint type. Here we use geometric Hecke orbits.
Using Theorem 2.4, we write our generalised Hecke orbit
as a finite union of geometric Hecke orbits. We define accordingly
As ![]() $Z$ is irreducible there at least one
$Z$ is irreducible there at least one ![]() $i\in \{0;\ldots ;k\}$ such that
$i\in \{0;\ldots ;k\}$ such that ![]() $\Sigma _i$ is Zariski dense in
$\Sigma _i$ is Zariski dense in ![]() $Z$.
$Z$.
Because the Galois representations ![]() $\rho _{x_1},\ldots,\rho _{x_k}$ of
$\rho _{x_1},\ldots,\rho _{x_k}$ of ![]() $x_1,\ldots,x_k$ can be deduced from
$x_1,\ldots,x_k$ can be deduced from ![]() $\rho _{x_0}$ using § 3, the Mumford–Tate hypothesis will still be valid even if we replace
$\rho _{x_0}$ using § 3, the Mumford–Tate hypothesis will still be valid even if we replace ![]() $x_0$ by
$x_0$ by ![]() $x_i$. We assume, for simplicity, that
$x_i$. We assume, for simplicity, that ![]() $x_i=x_0$.
$x_i=x_0$.
We choose an open compact subgroup ![]() $K'\leq G^{\rm ad}({\mathbb {A}}_f)$ so that we can consider the Shimura morphism
$K'\leq G^{\rm ad}({\mathbb {A}}_f)$ so that we can consider the Shimura morphism
Let ![]() $Z'$ be the image of
$Z'$ be the image of ![]() $Z$. One knows that
$Z$. One knows that ![]() $Z$ is weakly special in
$Z$ is weakly special in ![]() $Sh_{K}(G,X)$ if and only if
$Sh_{K}(G,X)$ if and only if ![]() $Z'$ is weakly special in
$Z'$ is weakly special in ![]() $Sh_{K'}(G^{\rm ad},X^{\rm ad})$.
$Sh_{K'}(G^{\rm ad},X^{\rm ad})$.
Then ![]() $\Psi (\Sigma _0)$ is dense in
$\Psi (\Sigma _0)$ is dense in ![]() $Z'$. Denote
$Z'$. Denote ![]() $x_0^{\rm ad}$ the image of
$x_0^{\rm ad}$ the image of ![]() $x_0$ in
$x_0$ in ![]() $X^{\rm ad}$, and define
$X^{\rm ad}$, and define
Using § 2.2.3, we get
and, thus, ![]() $\Sigma '$ is Zariski dense in
$\Sigma '$ is Zariski dense in ![]() $Z'$.
$Z'$.
Let ![]() $M'$ be the image of
$M'$ be the image of ![]() $M$ by
$M$ by ![]() $ad_G:G\to G^{\rm ad}$. Then
$ad_G:G\to G^{\rm ad}$. Then ![]() $M^{\rm ad}\simeq M'^{\rm ad}$ because
$M^{\rm ad}\simeq M'^{\rm ad}$ because ![]() $\ker (ad_G)$ is commutative and central in
$\ker (ad_G)$ is commutative and central in ![]() $G$. In view of § 6, the Mumford–Tate hypothesis will still hold for
$G$. In view of § 6, the Mumford–Tate hypothesis will still hold for ![]() $x_0^{\rm ad}\in X^{\rm ad}$.
$x_0^{\rm ad}\in X^{\rm ad}$.
Thus, we can, and will, assume ![]() $G=G^{\rm ad}$.
$G=G^{\rm ad}$.
7.1.3 Induction argument for factorisable subvarieties
The following reduction will be useful at the very end of the whole proof.
We recall that ![]() $G$ is a direct product
$G$ is a direct product ![]() $G_1\times \cdots \times G_f$ of its
$G_1\times \cdots \times G_f$ of its ![]() ${\mathbb {Q}}$-simple subgroups.
${\mathbb {Q}}$-simple subgroups.
It can be easily proved that in the Theorem 1.2 we can replace ![]() $K$ by any other compact open subgroup. After possibly replacing
$K$ by any other compact open subgroup. After possibly replacing ![]() $K$ by the open subgroup
$K$ by the open subgroup ![]() $\prod _{i=1}^{f}K_i:=\prod _{i=1}^{f} K\cap G_i({\mathbb {A}}_f)$, there are factorisations
$\prod _{i=1}^{f}K_i:=\prod _{i=1}^{f} K\cap G_i({\mathbb {A}}_f)$, there are factorisations ![]() $X=\prod _{i=1}^{f} X_i$ and
$X=\prod _{i=1}^{f} X_i$ and
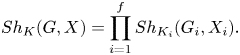 \begin{equation} Sh_K(G,X)=\prod_{i=1}^{f} Sh_{K_i}(G_i,X_i). \end{equation}
\begin{equation} Sh_K(G,X)=\prod_{i=1}^{f} Sh_{K_i}(G_i,X_i). \end{equation}
The factorisation (57) is defined over the reflex field ![]() $E(G,X)$, hence over
$E(G,X)$, hence over ![]() $E$. Consider a nontrivial partition
$E$. Consider a nontrivial partition ![]() $\{1;\ldots ;f\}=I\sqcup J$ and the corresponding nontrivial factorisation of Shimura data
$\{1;\ldots ;f\}=I\sqcup J$ and the corresponding nontrivial factorisation of Shimura data
with
By functoriality (§ 3.2) for ![]() $\phi =p_I\circ \phi _0$ (respectively,
$\phi =p_I\circ \phi _0$ (respectively, ![]() $\phi =p_J\circ \phi _0$), we will have
$\phi =p_J\circ \phi _0$), we will have
As explained in § 6, the Mumford–Tate hypothesis will hold for ![]() $p_I(x_0)$ and for
$p_I(x_0)$ and for ![]() $p_J(x_0)$.
$p_J(x_0)$.
Suppose that ![]() $Z$ factors as a Cartesian product
$Z$ factors as a Cartesian product
in the corresponding factorisation of Shimura varieties. From § 2.2.2, we have
and
Recall that the partition ![]() $\{1;\ldots ;f\}=I\sqcup J$ is not trivial. Arguing by induction on
$\{1;\ldots ;f\}=I\sqcup J$ is not trivial. Arguing by induction on ![]() $f$, we can assume that Theorem 1.2 is proven for
$f$, we can assume that Theorem 1.2 is proven for ![]() $Z_I$ and
$Z_I$ and ![]() $Z_J$. Then
$Z_J$. Then ![]() $Z_I\times Z_J$ is also a weakly special subvariety and we are done.
$Z_I\times Z_J$ is also a weakly special subvariety and we are done.
Henceforth, we assume that for every nontrivial partition ![]() $\{1;\ldots ;f\}=I\sqcup J$, the variety
$\{1;\ldots ;f\}=I\sqcup J$, the variety ![]() $Z$ is not a product of the form (58).
$Z$ is not a product of the form (58).
7.2 Central arguments
Let us recollect some of the notation and notions we will be using.
We have an irreducible subvariety ![]() $Z$ of
$Z$ of ![]() ${\rm Sh}_K(G,X)$ containing a Zariski-dense subset
${\rm Sh}_K(G,X)$ containing a Zariski-dense subset ![]() $\Sigma$ contained in the generalised Hecke orbit
$\Sigma$ contained in the generalised Hecke orbit ![]() $\mathcal {H}([x_0,1])$ of the point
$\mathcal {H}([x_0,1])$ of the point ![]() $[x_0,1]$. Let
$[x_0,1]$. Let ![]() $E$ be a field of finite type over
$E$ be a field of finite type over ![]() ${\mathbb {Q}}$ such that
${\mathbb {Q}}$ such that ![]() $Z$ and
$Z$ and ![]() $[x_0,1]$ are defined over
$[x_0,1]$ are defined over ![]() $E$, and passing to a finite extension we have a Galois representation
$E$, and passing to a finite extension we have a Galois representation ![]() $\rho :{\rm Gal}(\overline {E}/E)\to M({\mathbb {A}}_f)\cap K$ as in Definition 3.1 and our main hypothesis is that its image
$\rho :{\rm Gal}(\overline {E}/E)\to M({\mathbb {A}}_f)\cap K$ as in Definition 3.1 and our main hypothesis is that its image ![]() $U:=\rho ({\rm Gal}(\overline {E}/E))$ satisfies Definition 6.3. Passing to a finite extension we also assume that
$U:=\rho ({\rm Gal}(\overline {E}/E))$ satisfies Definition 6.3. Passing to a finite extension we also assume that ![]() $E$ is a field of definition for every geometric component of
$E$ is a field of definition for every geometric component of ![]() $Sh_K(G,X)$.
$Sh_K(G,X)$.
We reduce Theorem 1.2 to the case where ![]() $\Sigma$ is contained in a single geometric Hecke orbit. According to Theorem 2.4 the generalised Hecke orbit is a finite union of geometric orbit, with
$\Sigma$ is contained in a single geometric Hecke orbit. According to Theorem 2.4 the generalised Hecke orbit is a finite union of geometric orbit, with ![]() $\phi _0:M\to G$ the identity map,
$\phi _0:M\to G$ the identity map,
As ![]() $Z$ is irreducible, at least one of the intersections
$Z$ is irreducible, at least one of the intersections ![]() $Z\cap \mathcal {H}^g([\phi _i\circ x_0,1])$ is Zariski dense in
$Z\cap \mathcal {H}^g([\phi _i\circ x_0,1])$ is Zariski dense in ![]() $Z$. From § 3.2, we obtain
$Z$. From § 3.2, we obtain ![]() $\rho _{\phi _i\circ x_0}=\phi _i\circ \rho _{x_0}$ and the MT hypothesis is still valid for
$\rho _{\phi _i\circ x_0}=\phi _i\circ \rho _{x_0}$ and the MT hypothesis is still valid for ![]() $\phi (U)$ in
$\phi (U)$ in ![]() $\phi (M)=M_{\phi _i\circ x_0}$. Without loss of generality, we may assume
$\phi (M)=M_{\phi _i\circ x_0}$. Without loss of generality, we may assume ![]() $\phi _i=\phi _0$, that is
$\phi _i=\phi _0$, that is ![]() $\phi _i\circ x_0=x_0$.
$\phi _i\circ x_0=x_0$.
We may also assume that ![]() $[x_0,1]\in Z$ and, thus, that
$[x_0,1]\in Z$ and, thus, that ![]() $Z$ is contained in the image of
$Z$ is contained in the image of ![]() $X\times \{1\}$ in
$X\times \{1\}$ in ![]() $Sh_K(G,X)$.
$Sh_K(G,X)$.
7.2.1 Covering by Siegel sets
We choose a minimal ![]() ${\mathbb {Q}}$-parabolic subgroup
${\mathbb {Q}}$-parabolic subgroup ![]() $P$ of
$P$ of ![]() $G$ and a maximal compact subgroup
$G$ and a maximal compact subgroup ![]() $K_\infty$ of
$K_\infty$ of ![]() $G({\mathbb {R}})^+$, for instance
$G({\mathbb {R}})^+$, for instance ![]() $K_{x_0}=Z_{G({\mathbb {R}})}(x_0)$. We define
$K_{x_0}=Z_{G({\mathbb {R}})}(x_0)$. We define
and denote by
the geometric component of ![]() $Sh_K(G,X)$ which is the image of
$Sh_K(G,X)$ which is the image of ![]() $X^+\times \{1\}$.
$X^+\times \{1\}$.
See Definition 5.10 for the definition of a Siegel set associated to ![]() $P$ and
$P$ and ![]() $K_\infty$. It is known that there is a finite set
$K_\infty$. It is known that there is a finite set ![]() $\{g_1;\ldots ;g_c\}\subseteq G({\mathbb {Q}})$ and Siegel sets
$\{g_1;\ldots ;g_c\}\subseteq G({\mathbb {Q}})$ and Siegel sets ![]() $\mathfrak {S}_1,\ldots,\mathfrak {S}_c$ associated to
$\mathfrak {S}_1,\ldots,\mathfrak {S}_c$ associated to ![]() $g_1P{g_1}^{-1},\ldots,g_cP{g_c}^{-1}$ and
$g_1P{g_1}^{-1},\ldots,g_cP{g_c}^{-1}$ and ![]() $K_\infty$ such that
$K_\infty$ such that ![]() $S^+$ is the image of
$S^+$ is the image of ![]() $\mathfrak {S}:=\mathfrak {S}_1\cup \cdots \cup \mathfrak {S}_c$.
$\mathfrak {S}:=\mathfrak {S}_1\cup \cdots \cup \mathfrak {S}_c$.
For each ![]() $\mathfrak {S}_i$, it is assumed that
$\mathfrak {S}_i$, it is assumed that ![]() $\Omega$ from Definition 5.10 is a bounded semialgebraic subset.
$\Omega$ from Definition 5.10 is a bounded semialgebraic subset.
Let ![]() $\mathfrak {S}_W=\mathfrak {S}/Z_{G({\mathbb {R}})}(M)$ be the image of
$\mathfrak {S}_W=\mathfrak {S}/Z_{G({\mathbb {R}})}(M)$ be the image of ![]() $\mathfrak {S}$ in
$\mathfrak {S}$ in ![]() $W^+({\mathbb {R}})$.
$W^+({\mathbb {R}})$.
The maps
are real algebraic and, thus, semialgebraic. It follows that ![]() $\mathfrak {S}_W$ is semialgebraic, that its image
$\mathfrak {S}_W$ is semialgebraic, that its image ![]() $\mathfrak {S}_X$ in
$\mathfrak {S}_X$ in ![]() $X$ is semialgebraic and that the map
$X$ is semialgebraic and that the map
is semialgebraic.
7.2.2 o-minimality
We use the theory of o-minimal structures and recall that the map
is definable in the o-minimal structure ![]() ${\mathbb {R}}_{an,\exp }$ by [Reference Klingler, Ullmo and YafaevKUY16]. As (60) is semialgebraic, it is definable in
${\mathbb {R}}_{an,\exp }$ by [Reference Klingler, Ullmo and YafaevKUY16]. As (60) is semialgebraic, it is definable in ![]() ${\mathbb {R}}_{an,\exp }$, and the following is definable in
${\mathbb {R}}_{an,\exp }$, and the following is definable in ![]() ${\mathbb {R}}_{an,\exp }$ as well
${\mathbb {R}}_{an,\exp }$ as well
The algebraic variety ![]() $Z$ is definable in
$Z$ is definable in ![]() ${\mathbb {R}}_{an,\exp }$ and its inverse image
${\mathbb {R}}_{an,\exp }$ and its inverse image
is definable in ![]() ${\mathbb {R}}_{an,\exp }$ as well.
${\mathbb {R}}_{an,\exp }$ as well.
Because ![]() $E$ is a field of definition for
$E$ is a field of definition for ![]() $Z$, for every
$Z$, for every ![]() $\sigma \in Gal(\overline {E}/E)$ and
$\sigma \in Gal(\overline {E}/E)$ and ![]() $z\in Z(\overline {E})$ we have
$z\in Z(\overline {E})$ we have ![]() $\sigma (z)\in Z$ and, finally,
$\sigma (z)\in Z$ and, finally,
Assume now that ![]() $z$ also belongs to
$z$ also belongs to ![]() $\mathcal {H}^g(x_0)$. For every
$\mathcal {H}^g(x_0)$. For every
we have ![]() $z'\in Z\subset S^+$ and we can find
$z'\in Z\subset S^+$ and we can find ![]() $\phi _{z'}\in W({\mathbb {Q}})$ such that
$\phi _{z'}\in W({\mathbb {Q}})$ such that
Because ![]() $\mathfrak {S}_X$ maps onto
$\mathfrak {S}_X$ maps onto ![]() $S^+$ we may assume that
$S^+$ we may assume that ![]() $\phi _{z'}\circ x_0\in \mathfrak {S}_X$. Equivalently, we have
$\phi _{z'}\circ x_0\in \mathfrak {S}_X$. Equivalently, we have
The set
maps onto ![]() $Gal(\overline {E}/E)\cdot z$ and we deduce
$Gal(\overline {E}/E)\cdot z$ and we deduce
7.2.3 Height bounds
We consider the affine embedding ![]() $\iota :W\to {\mathbb {A}}^{\dim (M)\cdot \dim (G)}$ of § 4.3. Let
$\iota :W\to {\mathbb {A}}^{\dim (M)\cdot \dim (G)}$ of § 4.3. Let ![]() $H_W$ and
$H_W$ and ![]() $H_f$ be as in (18).
$H_f$ be as in (18).
We can, of course, assume that ![]() $Z$ is infinite, and because
$Z$ is infinite, and because
is Zariski dense, it is infinite as well, and we can choose an infinite sequence ![]() $(z_n)_{n\in {\mathbb {Z}}_{\geq ~1}}$ of pairwise distinct
$(z_n)_{n\in {\mathbb {Z}}_{\geq ~1}}$ of pairwise distinct ![]() $z_n\in \Sigma$. We also assume that this sequence is Zariski generic in
$z_n\in \Sigma$. We also assume that this sequence is Zariski generic in ![]() $Z$.
$Z$.
By hypothesis, Definitions 6.1 and 6.3 apply, and thus we invoke Theorem 6.4 and, by Proposition 3.6, use it for Galois orbits. We have
Thanks to the height comparison Theorem 5.16, we have
It follows
More precisely, there are ![]() $a,b\in {\mathbb {R}}_{>0}$ such that
$a,b\in {\mathbb {R}}_{>0}$ such that
Using (61) we deduce
From Proposition 4.3 we have
and because ![]() $H_f(\phi )$ only depends on
$H_f(\phi )$ only depends on ![]() $[\phi \circ x_0,1]$ we have
$[\phi \circ x_0,1]$ we have
We make (62) precise by choosing ![]() $a',b'$ such that
$a',b'$ such that
For ![]() $\phi \in Q(z_n)\subset W({\mathbb {Q}})\cap \mathfrak {S}_W$ we get
$\phi \in Q(z_n)\subset W({\mathbb {Q}})\cap \mathfrak {S}_W$ we get
Writing ![]() $k(n)=H_f(\phi _{z_n})$, we deduce from the above that the subset
$k(n)=H_f(\phi _{z_n})$, we deduce from the above that the subset ![]() $Q(z_n)\subseteq \tilde {Z}\cap W({\mathbb {Q}})$ contains at least
$Q(z_n)\subseteq \tilde {Z}\cap W({\mathbb {Q}})$ contains at least ![]() $a+k(n)^b$ points of
$a+k(n)^b$ points of ![]() $H_W$-height at most
$H_W$-height at most ![]() $a'+k(n)^{b'}$.
$a'+k(n)^{b'}$.
Because the ![]() $z_n$ are distinct, so are the inverse images
$z_n$ are distinct, so are the inverse images ![]() $\phi _{z_n}$, and by the Northcott theorem we deduce that
$\phi _{z_n}$, and by the Northcott theorem we deduce that ![]() $H_W(\phi _{z_n})\to +\infty$ and, thus,
$H_W(\phi _{z_n})\to +\infty$ and, thus, ![]() $k(n)\to +\infty$.
$k(n)\to +\infty$.
We are ready to use the Pila–Wilkie theorem.
7.2.4 Pila–Wilkie theorem
We use the form Theorem 7.1 of the Pila–Wilkie theorem. We denote ![]() $K^{{\mathbb {R}}}_\infty$ the real algebraic group corresponding to
$K^{{\mathbb {R}}}_\infty$ the real algebraic group corresponding to ![]() $K_\infty$, and
$K_\infty$, and ![]() $X_{\mathbb {R}}$ the algebraic variety
$X_{\mathbb {R}}$ the algebraic variety ![]() $G_{\mathbb {R}}/K^{{\mathbb {R}}}_\infty$ over
$G_{\mathbb {R}}/K^{{\mathbb {R}}}_\infty$ over ![]() ${\mathbb {R}}$ (we have
${\mathbb {R}}$ (we have ![]() $X\subset X_{\mathbb {R}}({\mathbb {R}})$). We apply Theorem 7.1 to the morphism
$X\subset X_{\mathbb {R}}({\mathbb {R}})$). We apply Theorem 7.1 to the morphism ![]() $p:W=G_{\mathbb {R}}/Z_{G_{\mathbb {R}}}(M)\to X_{\mathbb {R}}= G_{\mathbb {R}}/K^{{\mathbb {R}}}_\infty$ and the definable subset
$p:W=G_{\mathbb {R}}/Z_{G_{\mathbb {R}}}(M)\to X_{\mathbb {R}}= G_{\mathbb {R}}/K^{{\mathbb {R}}}_\infty$ and the definable subset
We deduce for every ![]() $n$ that
$n$ that
Thus, for ![]() $n\gg 0$, we have
$n\gg 0$, we have
In other terms, for almost every ![]() $n$, there exist
$n$, there exist ![]() $\phi \in Q(z_n)$, and a non-zero-dimensional semialgebraic subset
$\phi \in Q(z_n)$, and a non-zero-dimensional semialgebraic subset ![]() $A_n\subset \tilde {Z}_X$, such that
$A_n\subset \tilde {Z}_X$, such that ![]() $\phi \circ x_0\in A_n$.
$\phi \circ x_0\in A_n$.
We will now use the hyperbolic Ax–Lindemann–Weierstrass theorem.
7.2.5 Functional transcendence
According to Ax–Lindemann–Weierstrass theorem (see [Reference Klingler, Ullmo and YafaevKUY16]), that for ![]() $n\gg 0$, there exists a weakly special subvariety
$n\gg 0$, there exists a weakly special subvariety ![]() $S'_n$ of
$S'_n$ of ![]() $S^+$ such that
$S^+$ such that
One can check that a weakly special subvariety containing a ![]() $\overline {E}$-valued point is defined over
$\overline {E}$-valued point is defined over ![]() $\overline {E}$. It follows that this
$\overline {E}$. It follows that this ![]() $S'_n$ is defined over
$S'_n$ is defined over ![]() $\overline {E}$, and applying
$\overline {E}$, and applying ![]() $\sigma \in Gal(\overline {E}/E)$ such that
$\sigma \in Gal(\overline {E}/E)$ such that ![]() $\sigma (z'_n)=z_n$, the conjugated subvariety
$\sigma (z'_n)=z_n$, the conjugated subvariety ![]() $S_n=\sigma (S'_n)$ will be: weakly special, contained in
$S_n=\sigma (S'_n)$ will be: weakly special, contained in ![]() $Z$ and containing
$Z$ and containing ![]() $z_n$.
$z_n$.
Because the sequence ![]() $z_n$ is generic in
$z_n$ is generic in ![]() $Z$, the family
$Z$, the family ![]() $(S_n)_{n\geq 0}$ is Zariski dense in
$(S_n)_{n\geq 0}$ is Zariski dense in ![]() $Z$.
$Z$.
Because ![]() $A_n$ has non-zero semialgebraic dimension, and
$A_n$ has non-zero semialgebraic dimension, and ![]() $\pi _{\mathfrak {S},X}$ has finite fibers, the image
$\pi _{\mathfrak {S},X}$ has finite fibers, the image ![]() $\pi _{\mathfrak {S},X}(A_n)$ has non-zero semialgebraic dimension, and
$\pi _{\mathfrak {S},X}(A_n)$ has non-zero semialgebraic dimension, and ![]() $S'_n$ has non-zero dimension as a variety, and
$S'_n$ has non-zero dimension as a variety, and ![]() $S_n$ also.
$S_n$ also.
We are ready to use the so-called geometric part of André–Oort conjecture.
7.2.6 Geometric André–Oort
We reuse the notation of § 7.1.3
From the geometric part of the André–Oort conjecture from [Reference UllmoUll14, Reference Richard and UllmoRU24], there exists a partition ![]() $\{1;\ldots ;c\}=I\sqcup J$, with
$\{1;\ldots ;c\}=I\sqcup J$, with ![]() $I\neq \emptyset$, but possibly
$I\neq \emptyset$, but possibly ![]() $J=\emptyset$, such that we have a factorisation
$J=\emptyset$, such that we have a factorisation
where ![]() $S_1$ is a geometric component of
$S_1$ is a geometric component of ![]() $Sh_{K_I}(G_I,X_I)$, and
$Sh_{K_I}(G_I,X_I)$, and ![]() $Z_J$ is a subvariety of
$Z_J$ is a subvariety of ![]() $Sh_{K_J}(G_J,X_J)$.
$Sh_{K_J}(G_J,X_J)$.
Because we assumed that ![]() $Z$ has no nontrivial factorisation, the partition
$Z$ has no nontrivial factorisation, the partition ![]() $\{1;\ldots ;c\}=I\sqcup J$ is trivial. We must have
$\{1;\ldots ;c\}=I\sqcup J$ is trivial. We must have ![]() $J=\emptyset$,
$J=\emptyset$, ![]() $I=\{1;\ldots ;c\}$. Equivalently,
$I=\{1;\ldots ;c\}$. Equivalently, ![]() $Z=S_1$. In other words,
$Z=S_1$. In other words, ![]() $Z$ is special and, in particular, is weakly special.
$Z$ is special and, in particular, is weakly special.
This finishes the proof of Theorem 1.2.
7.3 Refined Pila–Wilkie theorem
The following is a variant of Pila–Wilkie Theorem, which replaces the ‘block version’ of the Pila–Wilkie theorem used by Orr. We believe this variant is easier to understand and use, and will be of independent interest.
We deduce the following from [Reference PilaPil09, Theorem 1.7].
Theorem 7.1 Let ![]() $W$ be an affine algebraic variety defined over
$W$ be an affine algebraic variety defined over ![]() ${\mathbb {Q}}$, let
${\mathbb {Q}}$, let ![]() $X$ be an affine algebraic variety over
$X$ be an affine algebraic variety over ![]() ${\mathbb {R}}$ and let
${\mathbb {R}}$ and let ![]() $p:W_{\mathbb {R}}\to X$ be a morphism of algebraic varieties defined over
$p:W_{\mathbb {R}}\to X$ be a morphism of algebraic varieties defined over ![]() ${\mathbb {R}}$.
${\mathbb {R}}$.
Let ![]() $Z\subset X({\mathbb {R}})$ be a definable subset, and denote
$Z\subset X({\mathbb {R}})$ be a definable subset, and denote ![]() $Z^{\rm alg}$ be the union of the semialgebraic subsets of
$Z^{\rm alg}$ be the union of the semialgebraic subsets of ![]() $X({\mathbb {R}})$ which are contained in
$X({\mathbb {R}})$ which are contained in ![]() $Z$ and of non-zero dimension.
$Z$ and of non-zero dimension.
We consider a height function ![]() $H_W$ on
$H_W$ on ![]() $W({\mathbb {Q}})$ associated to some affine embedding. Then
$W({\mathbb {Q}})$ associated to some affine embedding. Then
Explicitly, for every ![]() $\epsilon \in {\mathbb {R}}_{>0}$, there exists
$\epsilon \in {\mathbb {R}}_{>0}$, there exists ![]() $C(\epsilon,Z)\in {\mathbb {R}}_{>0}$, such that
$C(\epsilon,Z)\in {\mathbb {R}}_{>0}$, such that
Comment
The theorem still holds with a semialgebraic map ![]() $p:W({\mathbb {R}})\to X({\mathbb {R}})$ instead of the real algebraic
$p:W({\mathbb {R}})\to X({\mathbb {R}})$ instead of the real algebraic ![]() $p:W_{\mathbb {R}}\to X$. This slight generalisation will not be needed.
$p:W_{\mathbb {R}}\to X$. This slight generalisation will not be needed.
The height function we use here is denoted by ![]() $H^{\text {proj}}$ by Pila, and is not the height function he uses in his statements. As mentioned in the introduction of [Reference PilaPil09], it is possible to invoke his statements with
$H^{\text {proj}}$ by Pila, and is not the height function he uses in his statements. As mentioned in the introduction of [Reference PilaPil09], it is possible to invoke his statements with ![]() $H^{\text {proj}}$ instead.
$H^{\text {proj}}$ instead.
Proof. We choose affine embeddings
defined over ![]() ${\mathbb {Q}}$ and
${\mathbb {Q}}$ and ![]() ${\mathbb {R}}$. We can then write the morphism
${\mathbb {R}}$. We can then write the morphism
with polynomials ![]() $P_1,\ldots,P_m\in {\mathbb {R}}[T_1,\ldots,T_n]$. Let
$P_1,\ldots,P_m\in {\mathbb {R}}[T_1,\ldots,T_n]$. Let ![]() $E$ be the finite-dimensional
$E$ be the finite-dimensional ![]() ${\mathbb {Q}}$-vector subspace of
${\mathbb {Q}}$-vector subspace of ![]() ${\mathbb {R}}$ generated by the coefficients of these polynomials.
${\mathbb {R}}$ generated by the coefficients of these polynomials.
We have
We choose an isomorphism ![]() $\iota :E\to {\mathbb {Q}}^d$ of
$\iota :E\to {\mathbb {Q}}^d$ of ![]() ${\mathbb {Q}}$ vector spaces. For every
${\mathbb {Q}}$ vector spaces. For every ![]() $P_i$, the map
$P_i$, the map
is polynomial with coefficients in ![]() ${\mathbb {Q}}$. This can be checked for every monomial of
${\mathbb {Q}}$. This can be checked for every monomial of ![]() $P_i$. The height on
$P_i$. The height on ![]() $E^m$ considered in [Reference PilaPil09, Theorem 1.7] can be written, with our notation,
$E^m$ considered in [Reference PilaPil09, Theorem 1.7] can be written, with our notation,
where ![]() $H$ is the usual height on
$H$ is the usual height on ![]() ${\mathbb {Q}}^{d\cdot m}$. It follows from the general ‘functoriality’ properties of heights of § 4.2 that
${\mathbb {Q}}^{d\cdot m}$. It follows from the general ‘functoriality’ properties of heights of § 4.2 that
Explicitly, for some ![]() $a,b\in {\mathbb {R}}_{>0}$ we have
$a,b\in {\mathbb {R}}_{>0}$ we have
We apply [Reference PilaPil09, Theorem 1.7] and obtain
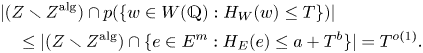 \begin{align*} &\lvert (Z\smallsetminus Z^{\rm alg})\cap p(\{w\in W({\mathbb{Q}}) : H_W(w)\leq T\}) \rvert\\ &\quad \leq \lvert (Z\smallsetminus Z^{\rm alg})\cap \{e\in E^m : H_E(e)\leq a+T^b\} \rvert=T^{o(1)}. \end{align*}
\begin{align*} &\lvert (Z\smallsetminus Z^{\rm alg})\cap p(\{w\in W({\mathbb{Q}}) : H_W(w)\leq T\}) \rvert\\ &\quad \leq \lvert (Z\smallsetminus Z^{\rm alg})\cap \{e\in E^m : H_E(e)\leq a+T^b\} \rvert=T^{o(1)}. \end{align*}
Appendix A. Exponentials of  $p$-adic matrices
$p$-adic matrices
In this appendix we fix a prime ![]() $p$, an integer
$p$, an integer ![]() $d\in {\mathbb {Z}}_{\geq 1}$, and denote by
$d\in {\mathbb {Z}}_{\geq 1}$, and denote by ![]() $M_d({\mathbb {Q}}_p)$ the space of square matrices of size
$M_d({\mathbb {Q}}_p)$ the space of square matrices of size ![]() $d$ with entries in
$d$ with entries in ![]() ${\mathbb {Q}}_p$. For
${\mathbb {Q}}_p$. For ![]() $Z\in M_d({\mathbb {Q}}_p)$ we denote by
$Z\in M_d({\mathbb {Q}}_p)$ we denote by ![]() $\chi _Z(T)=\det (TZ-1)\in {\mathbb {Q}}_p[T]$ its characteristic polynomial. Let
$\chi _Z(T)=\det (TZ-1)\in {\mathbb {Q}}_p[T]$ its characteristic polynomial. Let ![]() $\lvert ~ \rvert$ be the normalised absolute value on
$\lvert ~ \rvert$ be the normalised absolute value on ![]() ${\mathbb {Q}}_p$, extended to
${\mathbb {Q}}_p$, extended to ![]() $\overline {{\mathbb {Q}}_p}$: we have
$\overline {{\mathbb {Q}}_p}$: we have ![]() $\lvert p \rvert =1/p$ and
$\lvert p \rvert =1/p$ and ![]() $\lvert 1/d \rvert \leq d$ for
$\lvert 1/d \rvert \leq d$ for ![]() $d\in {\mathbb {Z}}_{\geq 1}$. We denote the norm of
$d\in {\mathbb {Z}}_{\geq 1}$. We denote the norm of ![]() $Z$, and the local height of
$Z$, and the local height of ![]() $Z$ by
$Z$ by
We define, whenever the corresponding series converges in ![]() $M_d({\mathbb {Q}}_p)$,
$M_d({\mathbb {Q}}_p)$,
 \[ \exp(Z)=\sum_{n\in{\mathbb{Z}}_{\geq0}} \frac{1}{n!}\cdot Z^n\quad \text{and} \quad \log(1+Z)= -\sum_{n\in{\mathbb{Z}}_{\geq 1}}\frac{(-1)^n}{n}\cdot Z^n. \]
\[ \exp(Z)=\sum_{n\in{\mathbb{Z}}_{\geq0}} \frac{1}{n!}\cdot Z^n\quad \text{and} \quad \log(1+Z)= -\sum_{n\in{\mathbb{Z}}_{\geq 1}}\frac{(-1)^n}{n}\cdot Z^n. \]
It is well known (see [Reference RobertRob00, Ch. 5. § 4.1]) that, on ![]() ${\mathbb {C}}_p$, the series
${\mathbb {C}}_p$, the series ![]() $\exp (T)$ has radius of convergence
$\exp (T)$ has radius of convergence ![]() $\lvert p \rvert ^{{1}/({p-1})}$ and the series
$\lvert p \rvert ^{{1}/({p-1})}$ and the series ![]() $\log (1+T)$ has radius of convergence
$\log (1+T)$ has radius of convergence ![]() $1$. It is also true that
$1$. It is also true that ![]() $\exp (Z)$, respectively,
$\exp (Z)$, respectively, ![]() $\log (1+Z)$ converges if and only if the eigenvalues of
$\log (1+Z)$ converges if and only if the eigenvalues of ![]() $Z$ are in the open disc of convergence of
$Z$ are in the open disc of convergence of ![]() $\exp (T)$ respectively,
$\exp (T)$ respectively, ![]() $\log (1+T)$. (For the archimedean case, see [Reference HighamHig08, § 1]. The relevant arguments carry over to ultrametric fields.)
$\log (1+T)$. (For the archimedean case, see [Reference HighamHig08, § 1]. The relevant arguments carry over to ultrametric fields.)
Proposition A.1 Let ![]() $Y\in M_d({\mathbb {Q}}_p)$ be such that
$Y\in M_d({\mathbb {Q}}_p)$ be such that ![]() $\log (1+Y)$ converges. Then
$\log (1+Y)$ converges. Then
Let ![]() $Y\in M_d({\mathbb {Q}}_p)$ be such that
$Y\in M_d({\mathbb {Q}}_p)$ be such that
Then ![]() $\log (1+Y)$ converges and we have:
$\log (1+Y)$ converges and we have:
– in general,
(A.3) \begin{equation} \lVert \log(1+Y) \rVert \leq d\cdot H_p(Y)^{d-1}; \end{equation}
\begin{equation} \lVert \log(1+Y) \rVert \leq d\cdot H_p(Y)^{d-1}; \end{equation}– and for
 $p>d$, the sharper estimate
(A.4)
$p>d$, the sharper estimate
(A.4) \begin{equation} \lVert \log(1+Y) \rVert \leq H_p(Y)^{d-1}. \end{equation}
\begin{equation} \lVert \log(1+Y) \rVert \leq H_p(Y)^{d-1}. \end{equation}
We deal with the first conclusion (A.1).
Proof. Let ![]() $\lambda _1,\ldots,\lambda _d$ be the eigenvalues of
$\lambda _1,\ldots,\lambda _d$ be the eigenvalues of ![]() $Y$, with repetitions. As can be seen on a Jordan form after passing to
$Y$, with repetitions. As can be seen on a Jordan form after passing to ![]() ${\mathbb {C}}_p$, the series
${\mathbb {C}}_p$, the series ![]() $\log (1+Y)$ converges if and only if every
$\log (1+Y)$ converges if and only if every ![]() $\log (\lambda _1),\ldots,\log (\lambda _d)$ converges. As the radius of convergence of
$\log (\lambda _1),\ldots,\log (\lambda _d)$ converges. As the radius of convergence of ![]() $\log (1+T)$ is
$\log (1+T)$ is ![]() $1$, this means
$1$, this means
Let ![]() $K={\mathbb {Q}}_p(\lambda _1,\ldots,\lambda _d)$, let
$K={\mathbb {Q}}_p(\lambda _1,\ldots,\lambda _d)$, let ![]() $O_K$ be its ring of integers, and
$O_K$ be its ring of integers, and ![]() $\mathfrak {m}_K$ be the maximal ideal of
$\mathfrak {m}_K$ be the maximal ideal of ![]() $O_K$. Then (A.5) means
$O_K$. Then (A.5) means
We deduce that the non-leading coefficients of
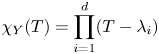 \[ \chi_Y(T)=\prod_{i=1}^d (T-\lambda_i) \]
\[ \chi_Y(T)=\prod_{i=1}^d (T-\lambda_i) \]
are in ![]() $\mathfrak {m}_K$. We recall that
$\mathfrak {m}_K$. We recall that ![]() ${\mathbb {Q}}_p\cap \mathfrak {m}_K=p{\mathbb {Z}}_p$ and
${\mathbb {Q}}_p\cap \mathfrak {m}_K=p{\mathbb {Z}}_p$ and ![]() $\chi _Y(T)\in {\mathbb {Q}}_p[T]$. We conclude that
$\chi _Y(T)\in {\mathbb {Q}}_p[T]$. We conclude that
We have proved (A.1) and before proving the rest of Proposition A.1, we prove an estimate on ![]() $\lVert Y^n \rVert$ for
$\lVert Y^n \rVert$ for ![]() $n\in {\mathbb {Z}}_{\geq 0}$.
$n\in {\mathbb {Z}}_{\geq 0}$.
Proof. We consider
By hypothesis, we have ![]() $\chi _Y(T)=c_0+\cdots +c_{d-1}T^{d-1}+T^d$ with
$\chi _Y(T)=c_0+\cdots +c_{d-1}T^{d-1}+T^d$ with ![]() $c_0,\ldots,c_{d-1}\in p{\mathbb {Z}}_p$. Let us first check that
$c_0,\ldots,c_{d-1}\in p{\mathbb {Z}}_p$. Let us first check that
on a generating family: for ![]() $0\leq i< d-1$ we have
$0\leq i< d-1$ we have ![]() $Y\cdot Y^i\in A$ by construction; for
$Y\cdot Y^i\in A$ by construction; for ![]() $i=d-1$ the identity
$i=d-1$ the identity ![]() $\chi _Y(Y)=0$ can be rearranged into
$\chi _Y(Y)=0$ can be rearranged into
Repeated use of (A.6) implies that, for ![]() $i\in {\mathbb {Z}}_{\geq 0}$, we have
$i\in {\mathbb {Z}}_{\geq 0}$, we have ![]() $Y^i A\subseteq A$. We deduce
$Y^i A\subseteq A$. We deduce ![]() $Y^i pA\subseteq pA$. But
$Y^i pA\subseteq pA$. But ![]() $Y^d\in pA$ by (A.7), hence
$Y^d\in pA$ by (A.7), hence ![]() $Y^d\cdot Y^i= Y^i\cdot Y^d\in pA$. Applied to
$Y^d\cdot Y^i= Y^i\cdot Y^d\in pA$. Applied to ![]() $i=0,\ldots,d-1$ it implies
$i=0,\ldots,d-1$ it implies ![]() $Y^d A\subseteq p A$ and by induction
$Y^d A\subseteq p A$ and by induction ![]() $(Y^d)^k A\subseteq p^k A$. We deduce again that
$(Y^d)^k A\subseteq p^k A$. We deduce again that ![]() $Y^i\cdot (Y^d)^k\in p^k A$. Writing
$Y^i\cdot (Y^d)^k\in p^k A$. Writing ![]() $n=k\cdot d+i$ with
$n=k\cdot d+i$ with ![]() $k=[{n}/{d}]$, we get the formula
$k=[{n}/{d}]$, we get the formula
and the bound
Using the ultrametric inequality ![]() $\lVert X+Z \rVert \leq \max \{\lVert X \rVert ;\lVert Z \rVert \}$ and submultiplicativity
$\lVert X+Z \rVert \leq \max \{\lVert X \rVert ;\lVert Z \rVert \}$ and submultiplicativity ![]() $\lVert X\times Z \rVert \leq \lVert X \rVert \cdot \lVert Z \rVert$ of the norm, we get
$\lVert X\times Z \rVert \leq \lVert X \rVert \cdot \lVert Z \rVert$ of the norm, we get
We apply our estimate to the series ![]() $\log (1+T)$ and finish the proof of Proposition A.1.
$\log (1+T)$ and finish the proof of Proposition A.1.
Proof. For the series ![]() $\log (1+Y)$ the above (A.8) and (A.9) imply the bound
$\log (1+Y)$ the above (A.8) and (A.9) imply the bound
We note that ![]() $\lim _{n\to \infty }\lvert {1}/{n} \rvert \cdot \lvert p \rvert ^{[{n}/{d}]}=0$ which implies that
$\lim _{n\to \infty }\lvert {1}/{n} \rvert \cdot \lvert p \rvert ^{[{n}/{d}]}=0$ which implies that ![]() $\log (1+Y)$ converges, and that
$\log (1+Y)$ converges, and that
By the ultrametric inequality and previous estimates,
As we used the normalised ![]() $p$-adic norm, we have
$p$-adic norm, we have ![]() $\lvert {1}/({d-1}) \rvert \leq d-1\leq d$ in general, and
$\lvert {1}/({d-1}) \rvert \leq d-1\leq d$ in general, and ![]() $\lvert {1}/({d-1}) \rvert =1$ if
$\lvert {1}/({d-1}) \rvert =1$ if ![]() $p\geq d$. This gives (A.3) and (A.4), respectively.
$p\geq d$. This gives (A.3) and (A.4), respectively.
The main statement of this appendix will require the following observation.
Lemma A.2 Let ![]() $Z \in M_d({\mathbb {Q}}_p)$ be such that
$Z \in M_d({\mathbb {Q}}_p)$ be such that ![]() $\exp (Z)$ converges and let us write
$\exp (Z)$ converges and let us write ![]() $\exp (Z)=1+Y$. Then
$\exp (Z)=1+Y$. Then ![]() $\log (1+Y)$ converges and
$\log (1+Y)$ converges and
Proof. For ![]() $d=1$, it is [Reference RobertRob00, § 5, Proposition 3].
$d=1$, it is [Reference RobertRob00, § 5, Proposition 3].
For ![]() $d>1$, it is [Reference RobertRob00, § 6.1.1] applied to
$d>1$, it is [Reference RobertRob00, § 6.1.1] applied to ![]() $(\partial /\partial Y)^i \log (1+Y)\circ \exp$.
$(\partial /\partial Y)^i \log (1+Y)\circ \exp$.
The following statement is one of our main tools for proving lower bounds for Galois orbits.
Theorem A.3 (Lemma of the exponentials)
Let ![]() $X \in M_d({\mathbb {Q}}_p)$ be such that
$X \in M_d({\mathbb {Q}}_p)$ be such that ![]() $\exp (X)$ converges and denote by
$\exp (X)$ converges and denote by ![]() $\exp (X)^{\mathbb {Z}}$ the subgroup generated by
$\exp (X)^{\mathbb {Z}}$ the subgroup generated by ![]() $\exp (X)$ in
$\exp (X)$ in ![]() $GL_d({\mathbb {Q}}_p)$.
$GL_d({\mathbb {Q}}_p)$.
Then:
– in general, we have
(A.11) \begin{equation} [\exp(X)^{\mathbb{Z}}:\exp(X)^{\mathbb{Z}}\cap GL_d({\mathbb{Z}}_p)]\geq H_p(X)/d; \end{equation}
\begin{equation} [\exp(X)^{\mathbb{Z}}:\exp(X)^{\mathbb{Z}}\cap GL_d({\mathbb{Z}}_p)]\geq H_p(X)/d; \end{equation}– if
 $p>d$, we have more sharply
(A.12)
$p>d$, we have more sharply
(A.12) \begin{equation} [\exp(X)^{\mathbb{Z}}:\exp(X)^{\mathbb{Z}}\cap GL_d({\mathbb{Z}}_p)]\geq H_p(X). \end{equation}
\begin{equation} [\exp(X)^{\mathbb{Z}}:\exp(X)^{\mathbb{Z}}\cap GL_d({\mathbb{Z}}_p)]\geq H_p(X). \end{equation}
Proof. For every ![]() $i\in {\mathbb {Z}}$, we know that if
$i\in {\mathbb {Z}}$, we know that if ![]() $\exp (X)$ converge, then
$\exp (X)$ converge, then ![]() $\exp (iX)$ converges as well, and we have
$\exp (iX)$ converges as well, and we have
By Lemma A.2, with ![]() $Y_i=\exp (i\cdot X)-1$, we have convergence and identity
$Y_i=\exp (i\cdot X)-1$, we have convergence and identity
Proposition A.1 gives
and, if ![]() $d\leq p$,
$d\leq p$,
Assume that
Then ![]() $H_p(1+Y_i)=H_p(\exp (X)^i)=1$, and (A.13), respectively, (A.14), specialises to
$H_p(1+Y_i)=H_p(\exp (X)^i)=1$, and (A.13), respectively, (A.14), specialises to
Recall that ![]() $\lvert i \rvert \leq {1}/{i}$ as we use the normalised
$\lvert i \rvert \leq {1}/{i}$ as we use the normalised ![]() $p$-adic absolute value. The conclusions (A.11), respectively, (A.12), follow.
$p$-adic absolute value. The conclusions (A.11), respectively, (A.12), follow.
We finish with a sufficient criterion for ![]() $\exp (X)$ to converge.
$\exp (X)$ to converge.
Theorem A.4 Let ![]() $X$ be a matrix in
$X$ be a matrix in ![]() $M_d({\mathbb {Q}}_p)$ and
$M_d({\mathbb {Q}}_p)$ and ![]() $b\in {\mathbb {Z}}_{\geq 1}$ be such that
$b\in {\mathbb {Z}}_{\geq 1}$ be such that
Then ![]() $\exp (X)$ converges.
$\exp (X)$ converges.
Proof. By the usual criterion, it is sufficient to prove that every eigenvalue ![]() $\lambda$ of
$\lambda$ of ![]() $X$ is in the open disc of convergence for
$X$ is in the open disc of convergence for ![]() $\exp (T)$. This amounts to proving the inequality
$\exp (T)$. This amounts to proving the inequality ![]() $\lvert \lambda \rvert <\lvert p \rvert ^{{1}/({p-1})}$.
$\lvert \lambda \rvert <\lvert p \rvert ^{{1}/({p-1})}$.
For any eigenvalue ![]() $\lambda$ of
$\lambda$ of ![]() $X$, we have
$X$, we have ![]() $\chi _X(\lambda )=0$, hence
$\chi _X(\lambda )=0$, hence ![]() $\lambda ^d \in p^k {\mathbb {Z}}_p[\lambda ]$ by assumption. It follows
$\lambda ^d \in p^k {\mathbb {Z}}_p[\lambda ]$ by assumption. It follows ![]() $|\lambda |^d \leq |p|^k$, that is
$|\lambda |^d \leq |p|^k$, that is ![]() $\lvert \lambda \rvert \leq \lvert p \rvert ^{{k}/{d}}$. Using the inequality
$\lvert \lambda \rvert \leq \lvert p \rvert ^{{k}/{d}}$. Using the inequality ![]() $d < k(p-1)$, it implies
$d < k(p-1)$, it implies ![]() $\lvert \lambda \rvert <\lvert p \rvert ^{{1}/({p-1})}$.
$\lvert \lambda \rvert <\lvert p \rvert ^{{1}/({p-1})}$.
Appendix B. Heights bounds for adelic orbits of linear groups
Our bound on ![]() $p$-adic exponentials is combined with structure theory of linear algebraic groups to obtain the following general lower bound. It is applied to Galois orbits in § 6.
$p$-adic exponentials is combined with structure theory of linear algebraic groups to obtain the following general lower bound. It is applied to Galois orbits in § 6.
Theorem B.1 Let ![]() $M\leq GL(N)$ be a linear algebraic subgroup defined over
$M\leq GL(N)$ be a linear algebraic subgroup defined over ![]() ${\mathbb {Q}}$, denote by
${\mathbb {Q}}$, denote by ![]() $\phi _0: M\to GL(N)$ the identity morphism and
$\phi _0: M\to GL(N)$ the identity morphism and ![]() $W$ the
$W$ the ![]() $GL(N)$-conjugacy class of
$GL(N)$-conjugacy class of ![]() $\phi _0$. We define
$\phi _0$. We define
We consider the standard Weil ![]() ${\mathbb {A}}_f$-height function, see (17),
${\mathbb {A}}_f$-height function, see (17),
given by ![]() $H_f(\Phi )=\min \{n\in {\mathbb {Z}}_{\geq 1} : n\Phi (\mathfrak {m}_{\widehat {{\mathbb {Z}}}})\subset \mathfrak {gl}(N,\widehat {{\mathbb {Z}}})\}.$
$H_f(\Phi )=\min \{n\in {\mathbb {Z}}_{\geq 1} : n\Phi (\mathfrak {m}_{\widehat {{\mathbb {Z}}}})\subset \mathfrak {gl}(N,\widehat {{\mathbb {Z}}})\}.$
There exists ![]() $c=c(\phi _0)\in {\mathbb {R}}_{>0}$ such that, as
$c=c(\phi _0)\in {\mathbb {R}}_{>0}$ such that, as ![]() $\phi$ ranges through
$\phi$ ranges through ![]() $W({\mathbb {A}}_f)$, we have
$W({\mathbb {A}}_f)$, we have
where ![]() $\omega (n)$ counts the number of prime factors of
$\omega (n)$ counts the number of prime factors of ![]() $n$.
$n$.
The proof of Theorem B.1 will start in Appendix B.1. We deduce from Theorem B.1 the following.
Corollary B.2 We have
and, if ![]() $M$ is reductive and connected and
$M$ is reductive and connected and ![]() $\iota :W\to {\mathbb {A}}^d$ is an affine embedding, then, as
$\iota :W\to {\mathbb {A}}^d$ is an affine embedding, then, as ![]() $\phi$ ranges through
$\phi$ ranges through ![]() $W({\mathbb {A}}_f)$,
$W({\mathbb {A}}_f)$,
Furthermore, for every ![]() $\Phi \in \mbox {Hom}(\mathfrak {m}\otimes {\mathbb {A}}_f,\mathfrak {gl}(N)\otimes {\mathbb {A}}_f)$, we have
$\Phi \in \mbox {Hom}(\mathfrak {m}\otimes {\mathbb {A}}_f,\mathfrak {gl}(N)\otimes {\mathbb {A}}_f)$, we have
Proof of Corollary B.2 One passes from (B.1) to (B.2) by recalling the known estimate (see [Reference Hardy and WrightHW79, 22.10])
As for (B.3), we know that ![]() $W$ is affine as
$W$ is affine as ![]() $M$ is reductive, and
$M$ is reductive, and ![]() $\phi \mapsto d\phi$ is an affine embedding because
$\phi \mapsto d\phi$ is an affine embedding because ![]() $M$ is connected. Lastly, two heights functions on
$M$ is connected. Lastly, two heights functions on ![]() $W$ are polynomially equivalent, so we may replace
$W$ are polynomially equivalent, so we may replace ![]() $H_{W,f}(\phi )$ by
$H_{W,f}(\phi )$ by ![]() $H_{f}(d\phi )$ and this follows from (B.2).
$H_{f}(d\phi )$ and this follows from (B.2).
The identity in (B.4) follows from the observations
and the defining property we provided: we have ![]() $n\cdot g\cdot \Phi (m\mathfrak {m}_{\widehat {{\mathbb {Z}}}})\subset \mathfrak {gl}(N,\widehat {{\mathbb {Z}}})$ if and only if
$n\cdot g\cdot \Phi (m\mathfrak {m}_{\widehat {{\mathbb {Z}}}})\subset \mathfrak {gl}(N,\widehat {{\mathbb {Z}}})$ if and only if
The combination of Theorem C.1 (C.1) with (B.3) gives the following.
Theorem B.3 Let ![]() $M\leq GL(N)$ be a connected reductive linear algebraic subgroup defined over
$M\leq GL(N)$ be a connected reductive linear algebraic subgroup defined over ![]() ${\mathbb {Q}}$, denote
${\mathbb {Q}}$, denote ![]() $\phi _0: M\to GL(N)$ the identity morphism and
$\phi _0: M\to GL(N)$ the identity morphism and ![]() $W$ the
$W$ the ![]() $GL(N)$-conjugacy class of
$GL(N)$-conjugacy class of ![]() $\phi _0$, and let
$\phi _0$, and let ![]() $\iota :W\to {\mathbb {A}}^d$ be an affine embedding. Then, as
$\iota :W\to {\mathbb {A}}^d$ be an affine embedding. Then, as ![]() $\phi$ ranges through
$\phi$ ranges through ![]() $W({\mathbb {A}}_f)$,
$W({\mathbb {A}}_f)$,
B.1 Proof of Theorem B.1
The global theorem B.1 will follow directly from (B.6) in the analogous local theorem below.
Theorem B.4 We keep ![]() $M$,
$M$, ![]() $\phi _0$,
$\phi _0$, ![]() $W$, and
$W$, and ![]() $H_f$ as in Theorem B.1.
$H_f$ as in Theorem B.1.
For every prime ![]() $p$, let
$p$, let ![]() $H_p:\mbox {Hom}(\mathfrak {m}\otimes {\mathbb {A}}_f,\mathfrak {gl}(N)\otimes {\mathbb {A}}_f)\to {\mathbb {Z}}_{\geq 1}$ be given by
$H_p:\mbox {Hom}(\mathfrak {m}\otimes {\mathbb {A}}_f,\mathfrak {gl}(N)\otimes {\mathbb {A}}_f)\to {\mathbb {Z}}_{\geq 1}$ be given by ![]() $H_p(\Phi )=\min \{p^k\in p^{{\mathbb {Z}}_{\geq 1}} : p^k\Phi (\mathfrak {m}_{{\mathbb {Z}}_p})\subset \mathfrak {gl}(N,{\mathbb {Z}}_p)\}$.
$H_p(\Phi )=\min \{p^k\in p^{{\mathbb {Z}}_{\geq 1}} : p^k\Phi (\mathfrak {m}_{{\mathbb {Z}}_p})\subset \mathfrak {gl}(N,{\mathbb {Z}}_p)\}$.
There exists ![]() $c=c(\phi _0)\in {\mathbb {R}}_{>0}$ such that, for every prime
$c=c(\phi _0)\in {\mathbb {R}}_{>0}$ such that, for every prime ![]() $p$, and every
$p$, and every ![]() $\phi \in W({\mathbb {Q}}_p)$,
$\phi \in W({\mathbb {Q}}_p)$,
and if ![]() $\mathfrak {m}_{{\mathbb {Z}}_p}$ is generated over
$\mathfrak {m}_{{\mathbb {Z}}_p}$ is generated over ![]() ${\mathbb {Z}}_p$ by nilpotent elements and
${\mathbb {Z}}_p$ by nilpotent elements and ![]() $p> N$,
$p> N$,
Here is how to deduce Theorem B.1 from Theorem B.4.
Proof. Let us multiply the inequalities (B.6) for the ![]() $\omega (H_f(d\phi ))$ primes dividing
$\omega (H_f(d\phi ))$ primes dividing ![]() $H_f(d\phi )$ with the trivial inequalities
$H_f(d\phi )$ with the trivial inequalities
for all the other primes. Then one can identify the product on both sides with the corresponding sides of (B.1).
Theorem B.4 will follow from different cases gathered in Theorem B.5.
Theorem B.5 We keep the notation from Theorem B.4. For every prime ![]() $p$, let
$p$, let ![]() $K_p:=GL(N,{\mathbb {Z}}_p)$ and, for any
$K_p:=GL(N,{\mathbb {Z}}_p)$ and, for any ![]() $U\leq G({\mathbb {Q}}_p)$, let
$U\leq G({\mathbb {Q}}_p)$, let ![]() $[U]_p:=[U:U\cap K_p]$. We write
$[U]_p:=[U:U\cap K_p]$. We write ![]() $N^*=\mathrm {lcm}(1,\ldots,N)$ so that
$N^*=\mathrm {lcm}(1,\ldots,N)$ so that ![]() $\lvert 1/N^* \rvert _p=p^{[\log _p(N)]}$ and
$\lvert 1/N^* \rvert _p=p^{[\log _p(N)]}$ and ![]() $\lvert N^* \rvert _p=1$ if
$\lvert N^* \rvert _p=1$ if ![]() $p>N$.
$p>N$.
(i) For every prime
 $p$ we have
$p$ we have  $\exp (2p\mathfrak {m}_{{\mathbb {Z}}_p})\leq M({\mathbb {Z}}_p)$ and
(B.8)
$\exp (2p\mathfrak {m}_{{\mathbb {Z}}_p})\leq M({\mathbb {Z}}_p)$ and
(B.8) \begin{equation} [\phi(\exp(2p\mathfrak{m}_{{\mathbb{Z}}_p}))]_p\geq \lvert 2pN^* \rvert_p\cdot H_p(d\phi)\geq \frac{1}{2Np}\cdot H_p(d\phi). \end{equation}
\begin{equation} [\phi(\exp(2p\mathfrak{m}_{{\mathbb{Z}}_p}))]_p\geq \lvert 2pN^* \rvert_p\cdot H_p(d\phi)\geq \frac{1}{2Np}\cdot H_p(d\phi). \end{equation}(ii) Assume that
 $M$ is unipotent or more generally that
$M$ is unipotent or more generally that  $\mathfrak {m}_{{\mathbb {Z}}_p}$ is generated over
$\mathfrak {m}_{{\mathbb {Z}}_p}$ is generated over  ${\mathbb {Z}}_p$ by nilpotent elements, then
(B.9)
${\mathbb {Z}}_p$ by nilpotent elements, then
(B.9) \begin{equation} [\phi(M({{\mathbb{Z}}}_p))]_p\geq \lvert N^* \rvert_p\cdot H_p(d\phi). \end{equation}
\begin{equation} [\phi(M({{\mathbb{Z}}}_p))]_p\geq \lvert N^* \rvert_p\cdot H_p(d\phi). \end{equation}(iii) Assume that
 $M$ is an algebraic torus. There is
$M$ is an algebraic torus. There is  $c_2=c_2(\phi _0)\in {\mathbb {R}}_{>0}$ such that for every prime
$c_2=c_2(\phi _0)\in {\mathbb {R}}_{>0}$ such that for every prime  $p$, and every
$p$, and every  $\phi \in W({\mathbb {Q}}_p)$,
(B.10)
$\phi \in W({\mathbb {Q}}_p)$,
(B.10) \begin{equation} \text{if $H_p(d\phi)\neq 1$ then } \left\lvert \frac{\phi(M({\mathbb{Z}}_p))}{\phi(\exp(2p\mathfrak{m}_{{\mathbb{Z}}_p})) \cdot\phi(M({\mathbb{Z}}_p))\cap K_p} \right\rvert \geq \frac{p}{c_2}. \end{equation}
\begin{equation} \text{if $H_p(d\phi)\neq 1$ then } \left\lvert \frac{\phi(M({\mathbb{Z}}_p))}{\phi(\exp(2p\mathfrak{m}_{{\mathbb{Z}}_p})) \cdot\phi(M({\mathbb{Z}}_p))\cap K_p} \right\rvert \geq \frac{p}{c_2}. \end{equation}
We deduce Theorem B.4 from Theorem B.5.
Proof. The bound (B.7) follows from (B.9), and the observation that ![]() $\lvert N^* \rvert _p=p^{[\log _p(N)]}=p^0=1$ for
$\lvert N^* \rvert _p=p^{[\log _p(N)]}=p^0=1$ for ![]() $p>N$.
$p>N$.
Let ![]() $U$ be the unipotent radical of
$U$ be the unipotent radical of ![]() $M^0$ and
$M^0$ and ![]() $L$ be a reductive Levi subgroup of
$L$ be a reductive Levi subgroup of ![]() $M^0$ so that we have the Levi decomposition
$M^0$ so that we have the Levi decomposition ![]() $\mathfrak {m}=\mathfrak {u}+\mathfrak {l}$. By the principle of Appendix B.1.1 we may assume
$\mathfrak {m}=\mathfrak {u}+\mathfrak {l}$. By the principle of Appendix B.1.1 we may assume ![]() $M=U$ or
$M=U$ or ![]() $M=L$.
$M=L$.
In the first case ![]() $M=U$, one deduces (B.6), with
$M=U$, one deduces (B.6), with ![]() $c=N^*\geq \lvert 1/N^* \rvert _p$, from (B.9).
$c=N^*\geq \lvert 1/N^* \rvert _p$, from (B.9).
In the second case, ![]() $M=L$ is reductive, and thus generated by algebraic tori. By the principle of Appendix B.1.1 we may assume that
$M=L$ is reductive, and thus generated by algebraic tori. By the principle of Appendix B.1.1 we may assume that ![]() $M$ is a torus.
$M$ is a torus.
Let us mention a simpler argument giving the following weaker conclusion, which is sufficient for the purpose of this article:
Proof. We know that ![]() $H_p(d\phi )$ is a power
$H_p(d\phi )$ is a power ![]() $p^k$ of
$p^k$ of ![]() $p$. For
$p$. For ![]() $k=0$, we may take
$k=0$, we may take ![]() $c=1$. For
$c=1$. For ![]() $k=1$ we deduce from conclusion (iii) of Theorem B.5 thatFootnote 18
$k=1$ we deduce from conclusion (iii) of Theorem B.5 thatFootnote 18
For ![]() $k\geq 2$, we have
$k\geq 2$, we have ![]() $H_p(d\phi )/p\geq \sqrt {H_p(d\phi )}$ and we take
$H_p(d\phi )/p\geq \sqrt {H_p(d\phi )}$ and we take ![]() $c_2=2N$ and use (B.8).
$c_2=2N$ and use (B.8).
We now explain how to improve upon the exponent ![]() $1/2$.
$1/2$.
We suppose that ![]() $p$ is large enough, that
$p$ is large enough, that ![]() $p\neq 2$, and that the reduction
$p\neq 2$, and that the reduction ![]() $T_{{\mathbb {F}}_p}$ of the torus
$T_{{\mathbb {F}}_p}$ of the torus ![]() $T=M$ is a torus over
$T=M$ is a torus over ![]() ${\mathbb {F}}_p$. Then
${\mathbb {F}}_p$. Then ![]() $T_{{\mathbb {F}}_p}({\mathbb {F}}_p)$ is diagonalisable over
$T_{{\mathbb {F}}_p}({\mathbb {F}}_p)$ is diagonalisable over ![]() $\overline {{\mathbb {F}}_p}$ and its elements have order prime to
$\overline {{\mathbb {F}}_p}$ and its elements have order prime to ![]() $p$ and, thus, the order
$p$ and, thus, the order ![]() $\lvert T_{{\mathbb {F}}_p}({\mathbb {F}}_p) \rvert$ is prime to
$\lvert T_{{\mathbb {F}}_p}({\mathbb {F}}_p) \rvert$ is prime to ![]() $p$.
$p$.
From the exact sequence
we deduce that ![]() $U_p:=\exp (p\mathfrak {t}_{{\mathbb {Z}}_p})\leq T({\mathbb {Z}}_p)$ is a topological
$U_p:=\exp (p\mathfrak {t}_{{\mathbb {Z}}_p})\leq T({\mathbb {Z}}_p)$ is a topological ![]() $p$-group and
$p$-group and ![]() ${T({\mathbb {Z}}_p)}/{U_p}\hookrightarrow T({\mathbb {F}}_p)$ has order prime to
${T({\mathbb {Z}}_p)}/{U_p}\hookrightarrow T({\mathbb {F}}_p)$ has order prime to ![]() $p$.
$p$.
For any open subgroup ![]() $H\leq T({\mathbb {Z}}_p)$, we have
$H\leq T({\mathbb {Z}}_p)$, we have
We now choose ![]() $H$ defined by
$H$ defined by ![]() $\phi (H)=K_p\cap \phi (T({\mathbb {Z}}_p))$. We have
$\phi (H)=K_p\cap \phi (T({\mathbb {Z}}_p))$. We have
and
Substituting (B.14) and (B.15) in (B.13) yields
We now use (B.13) and (B.8) and (B.10) from Theorem B.5 and conclude
We now prove Theorem B.5.
Proof of conclusion (i) Assume for now the claim that ![]() $\exp$ converges on
$\exp$ converges on ![]() $2p\mathfrak {m}_{{\mathbb {Z}}_p}$ and
$2p\mathfrak {m}_{{\mathbb {Z}}_p}$ and ![]() $U:=\exp (2p\mathfrak {m}_{{\mathbb {Z}}_p})\leq M({\mathbb {Z}}_p)$. Let
$U:=\exp (2p\mathfrak {m}_{{\mathbb {Z}}_p})\leq M({\mathbb {Z}}_p)$. Let ![]() $X_1,\ldots,X_k$ be generators of
$X_1,\ldots,X_k$ be generators of ![]() $\mathfrak {m}_{{\mathbb {Z}}_p}$, then
$\mathfrak {m}_{{\mathbb {Z}}_p}$, then
As ![]() $U_i:=\exp (2pX_i)^{\mathbb {Z}}\leq U$ for every
$U_i:=\exp (2pX_i)^{\mathbb {Z}}\leq U$ for every ![]() $i\in \{1;\ldots ;k\}$ we have
$i\in \{1;\ldots ;k\}$ we have
and, thus,
According to Theorem A.3 for ![]() $X=2p\cdot d\phi (X_i)$ we have
$X=2p\cdot d\phi (X_i)$ we have
We remark
Substituting (B.20) into (B.19) and (B.19) into (B.18), we get
We now recall why, for ![]() $2pX\in 2p\mathfrak {m}_{{\mathbb {Z}}_p}$, the series
$2pX\in 2p\mathfrak {m}_{{\mathbb {Z}}_p}$, the series ![]() $\exp (2pX)$ converges and
$\exp (2pX)$ converges and ![]() $\exp (2pX)\in M({\mathbb {Z}}_p)$ for
$\exp (2pX)\in M({\mathbb {Z}}_p)$ for ![]() $2pX\in 2p\mathfrak {m}_{{\mathbb {Z}}_p}$.
$2pX\in 2p\mathfrak {m}_{{\mathbb {Z}}_p}$.
Proof. We remark that ![]() $\exp (2pT)\in {\mathbb {Z}}_{(p)}[[T]]$ and recall that the
$\exp (2pT)\in {\mathbb {Z}}_{(p)}[[T]]$ and recall that the ![]() $p$-adic radius of convergence of
$p$-adic radius of convergence of ![]() $\exp (2pT)$ is
$\exp (2pT)$ is ![]() $2\cdot p/ p^{{1}/({p-1})}>1$. For
$2\cdot p/ p^{{1}/({p-1})}>1$. For ![]() $2pX\in 2p\mathfrak {m}_{{\mathbb {Z}}_p}$, we have
$2pX\in 2p\mathfrak {m}_{{\mathbb {Z}}_p}$, we have ![]() $\lVert X \rVert \leq 1$ and so
$\lVert X \rVert \leq 1$ and so ![]() $\exp (2pX)$ converges. We have
$\exp (2pX)$ converges. We have ![]() $\exp (2pX)\in M(d,{\mathbb {Z}}_p)$ because
$\exp (2pX)\in M(d,{\mathbb {Z}}_p)$ because ![]() $\exp (2pT)\in {\mathbb {Z}}_p[[X]]$ has
$\exp (2pT)\in {\mathbb {Z}}_p[[X]]$ has ![]() ${\mathbb {Z}}_p$ entries. Likewise, and
${\mathbb {Z}}_p$ entries. Likewise, and ![]() $\exp (2pX)^{-1}=\exp (-2pX)\in M(d,{\mathbb {Z}}_p)$ and we conclude
$\exp (2pX)^{-1}=\exp (-2pX)\in M(d,{\mathbb {Z}}_p)$ and we conclude ![]() $\exp (2pX)\in GL(N,{\mathbb {Z}}_p)$.
$\exp (2pX)\in GL(N,{\mathbb {Z}}_p)$.
Conclusion (i) has been proved.
Proof of conclusion (ii) Let ![]() $X_1,\ldots,X_k$ be a nilpotent basis of
$X_1,\ldots,X_k$ be a nilpotent basis of ![]() $\mathfrak {m}_{{\mathbb {Z}}_p}$. Then the
$\mathfrak {m}_{{\mathbb {Z}}_p}$. Then the ![]() $d\phi (X_1),\ldots,d\phi (X_k)$ generate
$d\phi (X_1),\ldots,d\phi (X_k)$ generate ![]() $d\phi (\mathfrak {m}_{{\mathbb {Z}}_p})$ and there exists an
$d\phi (\mathfrak {m}_{{\mathbb {Z}}_p})$ and there exists an ![]() $i\in \{1;\ldots ;k\}$ such that
$i\in \{1;\ldots ;k\}$ such that ![]() $H_p(d\phi )=H_p(d\phi (X_i))$. Because
$H_p(d\phi )=H_p(d\phi (X_i))$. Because ![]() $X_i$ is nilpotent, we have
$X_i$ is nilpotent, we have
and, thus, ![]() $\exp (N^*\cdot X_i)\in M({\mathbb {Z}}_p)$.
$\exp (N^*\cdot X_i)\in M({\mathbb {Z}}_p)$.
Thus,
Finally, by (A.11), we have
Because ![]() $H_p(d\phi (N^*\cdot X_i))$ and
$H_p(d\phi (N^*\cdot X_i))$ and ![]() $[\phi (\exp (N^*\cdot X_i\cdot {\mathbb {Z}}_p))]_p$ are powers of
$[\phi (\exp (N^*\cdot X_i\cdot {\mathbb {Z}}_p))]_p$ are powers of ![]() $p$, we actually have
$p$, we actually have
Conclusion (iii) is due to [Reference Edixhoven and YafaevEY03] and we detail how their formulation [Reference Edixhoven and YafaevEY03, Proposition 4.3.9] relates to ours.
Proof of conclusion (iii) We can discard finitely many primes and assume ![]() $p$ is big enough so that [Reference Edixhoven and YafaevEY03, Proposition 4.3.9] and its proof applies.
$p$ is big enough so that [Reference Edixhoven and YafaevEY03, Proposition 4.3.9] and its proof applies.
We first note that, in the matrix algebra ![]() $M(N,{\mathbb {Q}})$, the subalgebra
$M(N,{\mathbb {Q}})$, the subalgebra ![]() ${\mathbb {Q}}[T({\mathbb {Q}})]$ contains
${\mathbb {Q}}[T({\mathbb {Q}})]$ contains ![]() $\mathfrak {t}$.
$\mathfrak {t}$.
Proof. The inclusion of vector spaces can be checked after passing to ![]() ${\mathbb {R}}/{\mathbb {Q}}$. We know that
${\mathbb {R}}/{\mathbb {Q}}$. We know that
because, by weak approximation, ![]() $T({\mathbb {Q}})$ is dense in
$T({\mathbb {Q}})$ is dense in ![]() $T({\mathbb {R}})$. Let
$T({\mathbb {R}})$. Let ![]() $t$ be a sufficiently small element in
$t$ be a sufficiently small element in ![]() $\mathfrak {t}\otimes {\mathbb {R}}$, so that
$\mathfrak {t}\otimes {\mathbb {R}}$, so that ![]() $\log (\exp (t))$ converges and
$\log (\exp (t))$ converges and ![]() $\log (\exp (t))=t$. Then
$\log (\exp (t))=t$. Then ![]() $t\in {\mathbb {R}}[\exp (t)]$, as is seen using Jordan forms, and
$t\in {\mathbb {R}}[\exp (t)]$, as is seen using Jordan forms, and ![]() $\exp (t)\in T({\mathbb {R}})$. Because
$\exp (t)\in T({\mathbb {R}})$. Because ![]() $\mathfrak {t}\otimes {\mathbb {R}}$ admits a basis of such elements, we can conclude.
$\mathfrak {t}\otimes {\mathbb {R}}$ admits a basis of such elements, we can conclude.
We can choose ![]() $t_1,\ldots,t_k$ in
$t_1,\ldots,t_k$ in ![]() ${\mathbb {Q}}[T({\mathbb {Q}})]$ so that
${\mathbb {Q}}[T({\mathbb {Q}})]$ so that
and, thus, ![]() $t_1\cdot {\mathbb {Z}}+\cdots +t_k\cdot {\mathbb {Z}}$ contains a lattice of
$t_1\cdot {\mathbb {Z}}+\cdots +t_k\cdot {\mathbb {Z}}$ contains a lattice of ![]() $\mathfrak {t}$. It will hence contain
$\mathfrak {t}$. It will hence contain ![]() $n\cdot (\mathfrak {t}\cap \mathfrak {gl}(N,{\mathbb {Z}}))$ for some commensurability index
$n\cdot (\mathfrak {t}\cap \mathfrak {gl}(N,{\mathbb {Z}}))$ for some commensurability index ![]() $n\in {\mathbb {Z}}_{\geq 1}$.
$n\in {\mathbb {Z}}_{\geq 1}$.
As we discard finitely many primes ![]() $p$, we may assume that
$p$, we may assume that ![]() $p$ do not divide the denominators of the
$p$ do not divide the denominators of the ![]() $t_i$ and do not divide
$t_i$ and do not divide ![]() $n$. We will then have
$n$. We will then have
and
and, applying ![]() $\otimes _{{\mathbb {Z}}_{(p)}}{\mathbb {Z}}_p$, we may replace
$\otimes _{{\mathbb {Z}}_{(p)}}{\mathbb {Z}}_p$, we may replace ![]() ${\mathbb {Z}}_{(p)}$ by
${\mathbb {Z}}_{(p)}$ by ![]() ${\mathbb {Z}}_p$.
${\mathbb {Z}}_p$.
Let ![]() $\phi \in W({\mathbb {Q}}_p)$. Using Theorem 2.11, we can write
$\phi \in W({\mathbb {Q}}_p)$. Using Theorem 2.11, we can write
for some ![]() $g\in GL(N,{\mathbb {Q}}_p)$. We assume
$g\in GL(N,{\mathbb {Q}}_p)$. We assume ![]() $H_p(d\phi )\neq 1$, that is
$H_p(d\phi )\neq 1$, that is
and, by (B.21), there is at least one ![]() $i\in \{1;\ldots ;k\}$ such that
$i\in \{1;\ldots ;k\}$ such that
Equivalently, ![]() $gt_ig^{-1}\not \in GL(N,{\mathbb {Z}}_p)$, which also means
$gt_ig^{-1}\not \in GL(N,{\mathbb {Z}}_p)$, which also means
As ![]() $t_i\in T({\mathbb {Z}}_p)$, this implies, in the sense of [Reference Edixhoven and YafaevEY03, Proposition 4.3.9] (for
$t_i\in T({\mathbb {Z}}_p)$, this implies, in the sense of [Reference Edixhoven and YafaevEY03, Proposition 4.3.9] (for ![]() $W_{{\mathbb {Z}}_p}=g{\mathbb {Z}}_p^d$),
$W_{{\mathbb {Z}}_p}=g{\mathbb {Z}}_p^d$),
Looking into the proof of [Reference Edixhoven and YafaevEY03, Proposition 4.3.9] we note that their lower bound is given by a lower bound of some orbit of ![]() $T({\mathbb {F}}_p)$, thus, in (B.12), there exists
$T({\mathbb {F}}_p)$, thus, in (B.12), there exists ![]() $n\in {\mathbb {Z}}_{\geq 1}$ such that
$n\in {\mathbb {Z}}_{\geq 1}$ such that ![]() $n$ divides
$n$ divides ![]() $\lvert T({\mathbb {F}}_p) \rvert$ and
$\lvert T({\mathbb {F}}_p) \rvert$ and
In the factorisation (B.16) the first factor in the right-hand side is a power of ![]() $p$ and prime to
$p$ and prime to ![]() $n$. Thus the inequality
$n$. Thus the inequality ![]() $[\phi (T({\mathbb {Z}}_p))]_p\geq n$ comes from the second factor, i.e. we have inequality of conclusion (iii).
$[\phi (T({\mathbb {Z}}_p))]_p\geq n$ comes from the second factor, i.e. we have inequality of conclusion (iii).
B.1.1 Subgroup principle
The following elementary lemmas were useful in passing to subgroups in the proofs of Theorems B.1, B.4 and B.5. Proofs are left to the reader.
Lemma B.6 (Global subgroup principle)
Let ![]() $M_1,\ldots,M_k\leq M \leq GL(N)$ be algebraic groups over
$M_1,\ldots,M_k\leq M \leq GL(N)$ be algebraic groups over ![]() ${\mathbb {Q}}$ such that
${\mathbb {Q}}$ such that ![]() $\mathfrak {m}_1+\cdots +\mathfrak {m}_k=\mathfrak {m}$.
$\mathfrak {m}_1+\cdots +\mathfrak {m}_k=\mathfrak {m}$.
(i) Then
(B.22a)and the index \begin{equation} \Lambda:=\mathfrak{m}_1\cap \mathfrak{gl}(N,{\mathbb{Z}})+\cdots+\mathfrak{m}_k\cap \mathfrak{gl}(N,{\mathbb{Z}})\leq\mathfrak{m}\cap \mathfrak{gl}(N,{\mathbb{Z}}) \end{equation}(B.22b)is finite. For every prime
\begin{equation} \Lambda:=\mathfrak{m}_1\cap \mathfrak{gl}(N,{\mathbb{Z}})+\cdots+\mathfrak{m}_k\cap \mathfrak{gl}(N,{\mathbb{Z}})\leq\mathfrak{m}\cap \mathfrak{gl}(N,{\mathbb{Z}}) \end{equation}(B.22b)is finite. For every prime \begin{equation} c=[\mathfrak{m}\cap \mathfrak{gl}(N,{\mathbb{Z}}):\Lambda] \end{equation}
\begin{equation} c=[\mathfrak{m}\cap \mathfrak{gl}(N,{\mathbb{Z}}):\Lambda] \end{equation} $p$, we have
(B.22c)and
$p$, we have
(B.22c)and \begin{equation} \Lambda\otimes{\mathbb{Z}}_p=\mathfrak{m}_1\otimes{\mathbb{Q}}_p\cap \mathfrak{gl}(N,{\mathbb{Z}}_p)+\cdots+\mathfrak{m}_k\otimes{\mathbb{Q}}_p\cap \mathfrak{gl}(N,{\mathbb{Z}}_p)\leq\mathfrak{m}\otimes{\mathbb{Q}}_p\cap \mathfrak{gl}(N,{\mathbb{Z}}_p) \end{equation}(B.22d)with
\begin{equation} \Lambda\otimes{\mathbb{Z}}_p=\mathfrak{m}_1\otimes{\mathbb{Q}}_p\cap \mathfrak{gl}(N,{\mathbb{Z}}_p)+\cdots+\mathfrak{m}_k\otimes{\mathbb{Q}}_p\cap \mathfrak{gl}(N,{\mathbb{Z}}_p)\leq\mathfrak{m}\otimes{\mathbb{Q}}_p\cap \mathfrak{gl}(N,{\mathbb{Z}}_p) \end{equation}(B.22d)with \begin{equation} [\mathfrak{m}\otimes{\mathbb{Q}}_p\cap \mathfrak{gl}(N,{\mathbb{Z}}_p):\Lambda\otimes{\mathbb{Z}}_p]=\lvert 1/c \rvert_p \end{equation}
\begin{equation} [\mathfrak{m}\otimes{\mathbb{Q}}_p\cap \mathfrak{gl}(N,{\mathbb{Z}}_p):\Lambda\otimes{\mathbb{Z}}_p]=\lvert 1/c \rvert_p \end{equation} $\lvert 1/c \rvert _p\leq c$ and
$\lvert 1/c \rvert _p\leq c$ and  $\lvert 1/c \rvert _p=1$ if
$\lvert 1/c \rvert _p=1$ if  $gcd(c,p)=1$.
$gcd(c,p)=1$.(ii) Assume, moreover, that for some morphism
 $\phi :M\to GL(d)$ defined over
$\phi :M\to GL(d)$ defined over  ${\mathbb {Q}}$, we have
(B.22e)Then we have, with
${\mathbb {Q}}$, we have
(B.22e)Then we have, with \begin{equation} [\phi(M_i(\widehat{{\mathbb{Z}}})):\phi(M_i(\widehat{{\mathbb{Z}}}))\cap GL(d,\widehat{{\mathbb{Z}}})]\geq\frac{H_f(d\phi)}{c_i}. \end{equation}
\begin{equation} [\phi(M_i(\widehat{{\mathbb{Z}}})):\phi(M_i(\widehat{{\mathbb{Z}}}))\cap GL(d,\widehat{{\mathbb{Z}}})]\geq\frac{H_f(d\phi)}{c_i}. \end{equation} $c=n\cdot \max \{c_1;\ldots ;c_k\}$,
(B.22f)
$c=n\cdot \max \{c_1;\ldots ;c_k\}$,
(B.22f) \begin{equation} [\phi(M(\widehat{{\mathbb{Z}}})):\phi(M(\widehat{{\mathbb{Z}}}))\cap GL(d,\widehat{{\mathbb{Z}}})]\geq\frac{H_f(d\phi)}{c}. \end{equation}
\begin{equation} [\phi(M(\widehat{{\mathbb{Z}}})):\phi(M(\widehat{{\mathbb{Z}}}))\cap GL(d,\widehat{{\mathbb{Z}}})]\geq\frac{H_f(d\phi)}{c}. \end{equation}
Lemma B.7 (Local subgroup principle)
Let ![]() $p$ be a prime and
$p$ be a prime and ![]() $M_1,\ldots,M_k\leq M \leq GL(N)$ be algebraic groups over
$M_1,\ldots,M_k\leq M \leq GL(N)$ be algebraic groups over ![]() ${\mathbb {Q}}_p$.
${\mathbb {Q}}_p$.
(i) Then
(B.23a) \begin{equation} [M({\mathbb{Z}}_p)]_p\geq \max_{i\in\{1;\ldots;k\}}[M_i({\mathbb{Z}}_p)]_p. \end{equation}
\begin{equation} [M({\mathbb{Z}}_p)]_p\geq \max_{i\in\{1;\ldots;k\}}[M_i({\mathbb{Z}}_p)]_p. \end{equation}(ii) Assume that
 $\mathfrak {m}_1+\cdots +\mathfrak {m}_k=\mathfrak {m}$, then the index
(B.23b)is a finite power of
$\mathfrak {m}_1+\cdots +\mathfrak {m}_k=\mathfrak {m}$, then the index
(B.23b)is a finite power of \begin{equation} [\mathfrak{m}_{{\mathbb{Z}}_p}:\Lambda]=n \end{equation}
\begin{equation} [\mathfrak{m}_{{\mathbb{Z}}_p}:\Lambda]=n \end{equation} $p$.
$p$.(iii) With
 $n$ as above, for any
$n$ as above, for any  ${\mathbb {Q}}_p$ linear map
${\mathbb {Q}}_p$ linear map  $\Phi :\mathfrak {m}\to \mathfrak {gl}(d,{\mathbb {Q}}_p)$, we have
(B.23c)
$\Phi :\mathfrak {m}\to \mathfrak {gl}(d,{\mathbb {Q}}_p)$, we have
(B.23c) \begin{equation} \frac{1}{n} H_p(\Phi)\leq \max_{i\in\{1;\ldots;k\}} H_p(\Phi|_{\mathfrak{m}_i})\leq H_p(\Phi). \end{equation}
\begin{equation} \frac{1}{n} H_p(\Phi)\leq \max_{i\in\{1;\ldots;k\}} H_p(\Phi|_{\mathfrak{m}_i})\leq H_p(\Phi). \end{equation}(iv) Assume, moreover, for some morphism
 $\phi :M\to GL(N)$ defined over
$\phi :M\to GL(N)$ defined over  ${\mathbb {Q}}_p$ that we have (B.23c) for
${\mathbb {Q}}_p$ that we have (B.23c) for  $\Phi =d\phi$ and that
(B.23d)Then we have, with
$\Phi =d\phi$ and that
(B.23d)Then we have, with \begin{equation} \forall \, i\in\{1;\ldots;k\},\ [M_i({\mathbb{Z}}_p)]_p\geq \frac{1}{c_i}\cdot H_p(d\phi). \end{equation}
\begin{equation} \forall \, i\in\{1;\ldots;k\},\ [M_i({\mathbb{Z}}_p)]_p\geq \frac{1}{c_i}\cdot H_p(d\phi). \end{equation} $c=n\cdot \max \{c_1;\ldots ;c_k\}$,
(B.23e)
$c=n\cdot \max \{c_1;\ldots ;c_k\}$,
(B.23e) \begin{equation} [M({\mathbb{Z}}_p)_p]\geq \frac{1}{c}\cdot H_p(d\phi). \end{equation}
\begin{equation} [M({\mathbb{Z}}_p)_p]\geq \frac{1}{c}\cdot H_p(d\phi). \end{equation}
Appendix C. Upper bound on Adelic orbits
In this appendix, we prove upper bounds on adelic orbits. Combined with Proposition 3.6 this implies corresponding upper bounds on Galois orbits. This is not used in the proof of our main result but we believe can be useful in other contexts.
Theorem C.1 Let ![]() $M\leq G$ be reductive groups over
$M\leq G$ be reductive groups over ![]() ${\mathbb {Q}}$,
${\mathbb {Q}}$, ![]() $K\leq G({\mathbb {A}}_f)$ be a compact open subgroup, and
$K\leq G({\mathbb {A}}_f)$ be a compact open subgroup, and ![]() $K_M\leq K\cap M({\mathbb {A}}_f)$ be a compact subgroup.
$K_M\leq K\cap M({\mathbb {A}}_f)$ be a compact subgroup.
Let ![]() $\phi _0:M\to G$ be the inclusion monomorphism, and
$\phi _0:M\to G$ be the inclusion monomorphism, and ![]() $W=G\cdot \phi _0$ be the conjugacy class of
$W=G\cdot \phi _0$ be the conjugacy class of ![]() $\phi _0$, as an algebraic variety.
$\phi _0$, as an algebraic variety.
Let ![]() $\iota :W\hookrightarrow {\mathbb {A}}^N$ be an affine embedding, and let
$\iota :W\hookrightarrow {\mathbb {A}}^N$ be an affine embedding, and let ![]() $H_f$ be as defined in (17). Then we have, as
$H_f$ be as defined in (17). Then we have, as ![]() $\phi$ describes
$\phi$ describes ![]() $W({\mathbb {A}}_f)$,
$W({\mathbb {A}}_f)$,
We prove a more precise version. Let ![]() $\rho :G\hookrightarrow GL(d)$ be a faithful representation and let us identify
$\rho :G\hookrightarrow GL(d)$ be a faithful representation and let us identify ![]() $G$ with
$G$ with ![]() $\rho (G)$. In the associative algebra
$\rho (G)$. In the associative algebra ![]() ${\rm End}({\mathbb {Q}}^d)$, we denote the subalgebras linearly generated by
${\rm End}({\mathbb {Q}}^d)$, we denote the subalgebras linearly generated by ![]() $M({\mathbb {Q}})$ and
$M({\mathbb {Q}})$ and ![]() $G({\mathbb {Q}})$ by
$G({\mathbb {Q}})$ by
Let ![]() $\Phi _0:B_M\to B_G$ denote the inclusion. We have
$\Phi _0:B_M\to B_G$ denote the inclusion. We have ![]() $M({\mathbb {Q}})\subseteq B_M$,
$M({\mathbb {Q}})\subseteq B_M$, ![]() $G({\mathbb {Q}})\subseteq B_G$, and
$G({\mathbb {Q}})\subseteq B_G$, and ![]() $\phi _0:M({\mathbb {Q}})\to G({\mathbb {Q}})$ is the restriction of
$\phi _0:M({\mathbb {Q}})\to G({\mathbb {Q}})$ is the restriction of ![]() $\Phi _0$.
$\Phi _0$.
For every field extension ![]() $L/{\mathbb {Q}}$, and
$L/{\mathbb {Q}}$, and ![]() $\phi =g\cdot \phi _0\cdot g^{-1}\in W(L)$, with
$\phi =g\cdot \phi _0\cdot g^{-1}\in W(L)$, with ![]() $g\in G(\overline {L})$, the map
$g\in G(\overline {L})$, the map
is a ![]() $L$-linear extension of
$L$-linear extension of ![]() $\phi$ to
$\phi$ to ![]() $B_M\otimes L$, and is the unique
$B_M\otimes L$, and is the unique ![]() $L$-linear extension.
$L$-linear extension.
We choose linear bases of ![]() $B_M$ and
$B_M$ and ![]() $B_G$ generating
$B_G$ generating ![]() $B_M\cap {\rm End}({\mathbb {Z}}^d)$ and
$B_M\cap {\rm End}({\mathbb {Z}}^d)$ and ![]() $B_G\cap {\rm End}({\mathbb {Z}}^d)$, respectively, and we consider the corresponding isomorphism
$B_G\cap {\rm End}({\mathbb {Z}}^d)$, respectively, and we consider the corresponding isomorphism ![]() $\mbox {Hom}(B_M,B_G)\simeq {\mathbb {Q}}^{\dim (B_M)\cdot \dim (B_G)}$. Then
$\mbox {Hom}(B_M,B_G)\simeq {\mathbb {Q}}^{\dim (B_M)\cdot \dim (B_G)}$. Then ![]() $\phi \mapsto B_\phi$ induces an affine embedding
$\phi \mapsto B_\phi$ induces an affine embedding ![]() $\iota _\rho :W\hookrightarrow \mbox {Hom}(B_M,B_G)\simeq {\mathbb {Q}}^{\dim (B_M)\cdot \dim (B_G)}$.
$\iota _\rho :W\hookrightarrow \mbox {Hom}(B_M,B_G)\simeq {\mathbb {Q}}^{\dim (B_M)\cdot \dim (B_G)}$.
Theorem C.2 Define ![]() $G(\widehat {{\mathbb {Z}}}):=G({\mathbb {A}}_f)\cap GL(d,\widehat {{\mathbb {Z}}})$ and
$G(\widehat {{\mathbb {Z}}}):=G({\mathbb {A}}_f)\cap GL(d,\widehat {{\mathbb {Z}}})$ and ![]() $M(\widehat {{\mathbb {Z}}}):=M({\mathbb {A}}_f)\cap GL(d,\widehat {{\mathbb {Z}}})$. Then, for every
$M(\widehat {{\mathbb {Z}}}):=M({\mathbb {A}}_f)\cap GL(d,\widehat {{\mathbb {Z}}})$. Then, for every ![]() $\phi \in W({\mathbb {A}}_f)$, we have
$\phi \in W({\mathbb {A}}_f)$, we have
We note that if ![]() $G$ is of adjoint type, we can use the adjoint representation and pick
$G$ is of adjoint type, we can use the adjoint representation and pick ![]() $d=\dim (G)$.
$d=\dim (G)$.
Let us prove Theorem C.2.
Proof. We endow ![]() $\mbox {Hom}(B_M\otimes {\mathbb {Q}}_p,B_G\otimes {\mathbb {Q}}_p)$ with the norm
$\mbox {Hom}(B_M\otimes {\mathbb {Q}}_p,B_G\otimes {\mathbb {Q}}_p)$ with the norm
We note that ![]() $H_{\iota _\rho,p}(\phi )=\max \{1;\lVert B_\phi \rVert \}$.
$H_{\iota _\rho,p}(\phi )=\max \{1;\lVert B_\phi \rVert \}$.
It suffices to prove that, for every prime ![]() $p$, and
$p$, and ![]() $\phi \in W({\mathbb {Q}}_p)$, we have
$\phi \in W({\mathbb {Q}}_p)$, we have
Let us write ![]() $\lVert B_\phi \rVert _p=p^k$. Then, in the notation of Lemma C.3, we have
$\lVert B_\phi \rVert _p=p^k$. Then, in the notation of Lemma C.3, we have
We deduce Theorem C.1 from Theorem C.2.
Proof. The assumptions imply the finiteness of
and
We have
By Proposition 4.1, we have ![]() $H_f\approx H_{\iota _\rho,f}$. Using (C.2), we conclude
$H_f\approx H_{\iota _\rho,f}$. Using (C.2), we conclude
Lemma C.3 Let ![]() $p$ be a prime,
$p$ be a prime, ![]() $d$ be in
$d$ be in ![]() ${\mathbb {Z}}_{\geq 0}$, and
${\mathbb {Z}}_{\geq 0}$, and ![]() $k$ be in
$k$ be in ![]() ${\mathbb {Z}}_{\geq 0}$.
${\mathbb {Z}}_{\geq 0}$.
Define ![]() $S(d,p,p^k)=\{b\in {\rm End}({\mathbb {Q}}_p^d):\lVert b \rVert \leq p^k, \det (b)\in {\mathbb {Z}}_p^\times \}$.
$S(d,p,p^k)=\{b\in {\rm End}({\mathbb {Q}}_p^d):\lVert b \rVert \leq p^k, \det (b)\in {\mathbb {Z}}_p^\times \}$.
Then ![]() $S(d,p,p^k)=S(d,p,p^k)\cdot GL(d,{\mathbb {Z}}_p)$ and
$S(d,p,p^k)=S(d,p,p^k)\cdot GL(d,{\mathbb {Z}}_p)$ and
Proof. We endow ![]() ${\rm End}({\mathbb {Q}}_p^d)$ with the additive Haar measure
${\rm End}({\mathbb {Q}}_p^d)$ with the additive Haar measure ![]() $\mu$ normalised by
$\mu$ normalised by ![]() $\mu (B(1))=1$, where
$\mu (B(1))=1$, where ![]() $B(p^k)$, for
$B(p^k)$, for ![]() $k\in {\mathbb {Z}}_{\geq 1}$ is the ball of radius
$k\in {\mathbb {Z}}_{\geq 1}$ is the ball of radius ![]() $p^k$. One knows that the Haar measure satisfies
$p^k$. One knows that the Haar measure satisfies ![]() $\mu (g\cdot A)=\lvert \det (g) \rvert \cdot \mu (A)$.
$\mu (g\cdot A)=\lvert \det (g) \rvert \cdot \mu (A)$.
For ![]() $A=B(1)$ and
$A=B(1)$ and ![]() $g=p^k\cdot \mathrm {Id}$ this yields
$g=p^k\cdot \mathrm {Id}$ this yields
For ![]() $b\in GL(N,{\mathbb {Q}}_p)$ such that
$b\in GL(N,{\mathbb {Q}}_p)$ such that ![]() $\det (b)\in {\mathbb {Z}}_p^\times$ this yields
$\det (b)\in {\mathbb {Z}}_p^\times$ this yields
One can also check
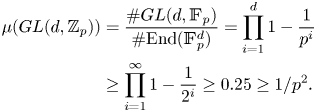 \begin{align} \mu(GL(d,{\mathbb{Z}}_p))&=\frac{\#GL(d,{\mathbb{F}}_p)}{\#{\rm End}({\mathbb{F}}_p^d)}= \prod_{i=1}^d1-\frac{1}{p^i} \nonumber\\ &\geq \prod_{i=1}^\infty 1-\frac{1}{2^i}\geq 0.25\geq 1/p^2. \end{align}
\begin{align} \mu(GL(d,{\mathbb{Z}}_p))&=\frac{\#GL(d,{\mathbb{F}}_p)}{\#{\rm End}({\mathbb{F}}_p^d)}= \prod_{i=1}^d1-\frac{1}{p^i} \nonumber\\ &\geq \prod_{i=1}^\infty 1-\frac{1}{2^i}\geq 0.25\geq 1/p^2. \end{align} The norm multiplicativity ![]() $\lVert b\cdot g \rVert =\lVert b \rVert \cdot \lVert g \rVert$ implies the right invariance
$\lVert b\cdot g \rVert =\lVert b \rVert \cdot \lVert g \rVert$ implies the right invariance
Equivalently, we can write
with ![]() $c=\#S(d,p,p^k)/GL(d,{\mathbb {Z}}_p)$.
$c=\#S(d,p,p^k)/GL(d,{\mathbb {Z}}_p)$.
Using (C.5), we deduce
Assume ![]() $k=0$. Then (C.4) follows from
$k=0$. Then (C.4) follows from
We may now assume ![]() $k\geq 1$. Then (C.4) follows from
$k\geq 1$. Then (C.4) follows from
Acknowledgements
The second named author has been contemplating the André–Pink–Zannier problem and how to use the Mumford–Tate conjecture to approach it for 20 years. He had a number of discussions on the subject with Bas Edixhoven, Richard Pink, Yves André, Emmanuel Ullmo, Bruno Klingler, Martin Orr, Christopher Daw, and more. Both authors would like to thank them all.
Conflicts of interest
None.
Financial support
Both authors were supported by Leverhulme Trust Grant RPG-2019-180. The first author is also supported by the EPSRC grant EP/Y020758/1. The support of the Leverhulme Trust is gratefully acknowledged.
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.


