Article contents
Local cohomology of Du Bois singularities and applications to families
Published online by Cambridge University Press: 27 July 2017
Abstract
In this paper we study the local cohomology modules of Du Bois singularities. Let 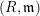 $(R,\mathfrak{m})$ be a local ring; we prove that if
$(R,\mathfrak{m})$ be a local ring; we prove that if 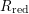 $R_{\text{red}}$ is Du Bois, then
$R_{\text{red}}$ is Du Bois, then 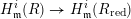 $H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R_{\text{red}})$ is surjective for every
$H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R_{\text{red}})$ is surjective for every 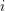 $i$ . We find many applications of this result. For example, we answer a question of Kovács and Schwede [Inversion of adjunction for rational and Du Bois pairs, Algebra Number Theory 10 (2016), 969–1000; MR 3531359] on the Cohen–Macaulay property of Du Bois singularities. We obtain results on the injectivity of
$i$ . We find many applications of this result. For example, we answer a question of Kovács and Schwede [Inversion of adjunction for rational and Du Bois pairs, Algebra Number Theory 10 (2016), 969–1000; MR 3531359] on the Cohen–Macaulay property of Du Bois singularities. We obtain results on the injectivity of 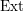 $\operatorname{Ext}$ that provide substantial partial answers to questions in Eisenbud et al. [Cohomology on toric varieties and local cohomology with monomial supports, J. Symbolic Comput. 29 (2000), 583–600] in characteristic
$\operatorname{Ext}$ that provide substantial partial answers to questions in Eisenbud et al. [Cohomology on toric varieties and local cohomology with monomial supports, J. Symbolic Comput. 29 (2000), 583–600] in characteristic 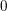 $0$ . These results can also be viewed as generalizations of the Kodaira vanishing theorem for Cohen–Macaulay Du Bois varieties. We prove results on the set-theoretic Cohen–Macaulayness of the defining ideal of Du Bois singularities, which are characteristic-
$0$ . These results can also be viewed as generalizations of the Kodaira vanishing theorem for Cohen–Macaulay Du Bois varieties. We prove results on the set-theoretic Cohen–Macaulayness of the defining ideal of Du Bois singularities, which are characteristic- 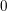 $0$ analogs and generalizations of results of Singh–Walther and answer some of their questions in Singh and Walther [On the arithmetic rank of certain Segre products, in Commutative algebra and algebraic geometry, Contemporary Mathematics, vol. 390 (American Mathematical Society, Providence, RI, 2005), 147–155]. We extend results on the relation between Koszul cohomology and local cohomology for
$0$ analogs and generalizations of results of Singh–Walther and answer some of their questions in Singh and Walther [On the arithmetic rank of certain Segre products, in Commutative algebra and algebraic geometry, Contemporary Mathematics, vol. 390 (American Mathematical Society, Providence, RI, 2005), 147–155]. We extend results on the relation between Koszul cohomology and local cohomology for 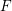 $F$ -injective and Du Bois singularities first shown in Hochster and Roberts [The purity of the Frobenius and local cohomology, Adv. Math. 21 (1976), 117–172; MR 0417172 (54 #5230)]. We also prove that singularities of dense
$F$ -injective and Du Bois singularities first shown in Hochster and Roberts [The purity of the Frobenius and local cohomology, Adv. Math. 21 (1976), 117–172; MR 0417172 (54 #5230)]. We also prove that singularities of dense 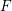 $F$ -injective type deform.
$F$ -injective type deform.
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2017
References
- 13
- Cited by

