No CrossRef data available.
Article contents
Tight bound for the Erdős–Pósa property of tree minors
Part of:
Graph theory
Published online by Cambridge University Press: 11 December 2024
Abstract
Let 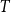 $T$ be a tree on
$T$ be a tree on  $t$ vertices. We prove that for every positive integer
$t$ vertices. We prove that for every positive integer 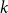 $k$ and every graph
$k$ and every graph 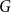 $G$, either
$G$, either 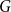 $G$ contains
$G$ contains 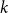 $k$ pairwise vertex-disjoint subgraphs each having a
$k$ pairwise vertex-disjoint subgraphs each having a 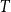 $T$ minor, or there exists a set
$T$ minor, or there exists a set 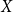 $X$ of at most
$X$ of at most 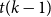 $t(k-1)$ vertices of
$t(k-1)$ vertices of 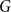 $G$ such that
$G$ such that 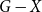 $G-X$ has no
$G-X$ has no 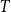 $T$ minor. The bound on the size of
$T$ minor. The bound on the size of 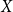 $X$ is best possible and improves on an earlier
$X$ is best possible and improves on an earlier 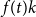 $f(t)k$ bound proved by Fiorini, Joret, and Wood (2013) with some fast-growing function
$f(t)k$ bound proved by Fiorini, Joret, and Wood (2013) with some fast-growing function 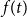 $f(t)$. Moreover, our proof is short and simple.
$f(t)$. Moreover, our proof is short and simple.
MSC classification
Primary:
05C83: Graph minors
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
Bienstock, D., Robertson, N., Seymour, P. and Thomas, R. (1991) Quickly excluding a forest. J. Comb. Theory, Series B 52 274–283.CrossRefGoogle Scholar
Cames van Batenburg, W., Huynh, T., Joret, G. and Raymond, J. F. (2019) A tight Erdős-Pósa function for planar minors. Adv. Comb. 10.Google Scholar
Chekuri, C. and Chuzhoy, J. (2013) Large-treewidth graph decompositions and applications. In Proceedings of the 45th annual ACM Symposium on Theory of Computing, ACM. pp. 291–300.CrossRefGoogle Scholar
Chekuri, C. and Chuzhoy, J. (2016) Polynomial bounds for the grid-minor theorem. J. ACM 63 40:1–40:65.CrossRefGoogle Scholar
Diestel, R. (1995) Graph minors 1: A short proof of the path-width theorem. Comb. Prob. Comp. 4 27–30.CrossRefGoogle Scholar
Erdős, P. and Pósa, L. (1965) On independent circuits contained in a graph. Canadian J. Math. 17 347–352.CrossRefGoogle Scholar
Fiorini, S., Joret, G. and Wood, D. R. (2013) Excluded forest minors and the Erdős-Pósa property. Comb. Prob. Comp. 22 700–721.CrossRefGoogle Scholar
Robertson, N. and Seymour, P. D. (1983) Graph minors. I. excluding a forest. J. Comb. Theory Series B 35 39–61.CrossRefGoogle Scholar
Robertson, N. and Seymour, P. D. (1986) Graph minors. V. Excluding a planar graph. J. Comb. Theory Series B 41 92–114.CrossRefGoogle Scholar


