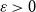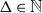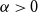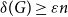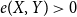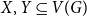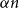1. Introduction
Determining the minimum degree condition for the existence of spanning structures is a central problem in extremal graph theory. The first result of this direction is Dirac’s theorem [Reference Dirac7] in 1952 which states that for
![]() $n\ge 3$
, every
$n\ge 3$
, every
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with
$G$
with
![]() $\delta (G)\ge \frac{n}{2}$
contains a Hamiltonian cycle. Komlós et al. [Reference Komlós, Sárközy and Szemerédi24] proved that an
$\delta (G)\ge \frac{n}{2}$
contains a Hamiltonian cycle. Komlós et al. [Reference Komlós, Sárközy and Szemerédi24] proved that an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with
$G$
with
![]() $\delta (G)\geq (\frac{1}{2}+o(1))n$
contains a copy of every bounded-degree spanning tree, and in [Reference Komlós, Sárközy and Szemerédi25], the result is extended to trees with maximum degree
$\delta (G)\geq (\frac{1}{2}+o(1))n$
contains a copy of every bounded-degree spanning tree, and in [Reference Komlós, Sárközy and Szemerédi25], the result is extended to trees with maximum degree
![]() $O(\frac{n}{\log n})$
. Another notable extension is the bandwidth theorem of Böttcher et al. [Reference Böttcher, Schacht and Taraz4], which finds the (asymptotically) optimal minimum degree condition forcing spanning subgraphs with bounded chromatic number and sublinear bandwidth and resolves a conjecture of Bollobás and Komlós [Reference Komlós23].
$O(\frac{n}{\log n})$
. Another notable extension is the bandwidth theorem of Böttcher et al. [Reference Böttcher, Schacht and Taraz4], which finds the (asymptotically) optimal minimum degree condition forcing spanning subgraphs with bounded chromatic number and sublinear bandwidth and resolves a conjecture of Bollobás and Komlós [Reference Komlós23].
Note that the extremal graphs in the above results usually have large independent sets, which makes them far from being typical. Hence a natural project is to study how the degree conditions drop if we forbid large independent sets from the host graph. Balogh et al. [Reference Balogh, Molla and Sharifzadeh1] initiated this study by proving if
![]() $G$
is an
$G$
is an
![]() $n$
-vertex graph with
$n$
-vertex graph with
![]() $\delta (G)\geq (\frac{1}{2}+o(1))n$
and
$\delta (G)\geq (\frac{1}{2}+o(1))n$
and
![]() $\alpha (G)=o(n)$
, then
$\alpha (G)=o(n)$
, then
![]() $G$
contains a
$G$
contains a
![]() $K_{3}$
-factor. This result is asymptotically optimal and requires a weaker degree bound than
$K_{3}$
-factor. This result is asymptotically optimal and requires a weaker degree bound than
![]() $\delta (G)\geq \frac{2}{3}n$
from the Corrádi–Hajnal theorem [Reference Corrádi and Hajnal6]. Nenadov and Pehova [Reference Nenadov and Pehova35] extended this result to the case of
$\delta (G)\geq \frac{2}{3}n$
from the Corrádi–Hajnal theorem [Reference Corrádi and Hajnal6]. Nenadov and Pehova [Reference Nenadov and Pehova35] extended this result to the case of
![]() $K_r$
-factor and asked for the best possible minimum degree condition on
$K_r$
-factor and asked for the best possible minimum degree condition on
![]() $G$
with
$G$
with
![]() $\alpha (G)=o(n)$
that guarantees a
$\alpha (G)=o(n)$
that guarantees a
![]() $K_r$
-factor. Knierim and Su [Reference Knierim and Su22] resolved this question for
$K_r$
-factor. Knierim and Su [Reference Knierim and Su22] resolved this question for
![]() $r\geq 4$
by showing
$r\geq 4$
by showing
![]() $\delta (G)\geq (\frac{r-2}{r}+o(1))n$
is asymptotically best possible. Nenadov and Pehova [Reference Nenadov and Pehova35] also generalised
$\delta (G)\geq (\frac{r-2}{r}+o(1))n$
is asymptotically best possible. Nenadov and Pehova [Reference Nenadov and Pehova35] also generalised
![]() $\alpha (G)$
into
$\alpha (G)$
into
![]() $\ell$
-independence number and this inspires several recent works [Reference Chang, Han, Kim, Wang and Yang5, Reference Han, Hu, Wang and Yang14, Reference Han, Morris, Wang and Yang15].
$\ell$
-independence number and this inspires several recent works [Reference Chang, Han, Kim, Wang and Yang5, Reference Han, Hu, Wang and Yang14, Reference Han, Morris, Wang and Yang15].
However, just excluding large independent sets is not enough to guarantee the existence of large connected subgraph. The union of two disjoint copies of
![]() $K_{\frac{n}{2}}$
has independence number two, but it does not contain any connected subgraphs with more than
$K_{\frac{n}{2}}$
has independence number two, but it does not contain any connected subgraphs with more than
![]() $\frac{n}{2}$
vertices. Hence it is necessary to impose stronger conditions to overcome this. The following notion of bipartite hole was introduced by McDiarmid and Yolov [Reference Mcdiarmid and Yolov33] in the study of Hamilton cycles. Given two disjoint vertex sets
$\frac{n}{2}$
vertices. Hence it is necessary to impose stronger conditions to overcome this. The following notion of bipartite hole was introduced by McDiarmid and Yolov [Reference Mcdiarmid and Yolov33] in the study of Hamilton cycles. Given two disjoint vertex sets
![]() $A$
and
$A$
and
![]() $B$
in a graph
$B$
in a graph
![]() $G$
, we use
$G$
, we use
![]() $E_{G}(A,B)$
to denote the set of edges joining
$E_{G}(A,B)$
to denote the set of edges joining
![]() $A$
and
$A$
and
![]() $B$
, and let
$B$
, and let
![]() $e_{G}(A,B)=\vert E_{G}(A,B) \vert$
. An
$e_{G}(A,B)=\vert E_{G}(A,B) \vert$
. An
![]() $(s,t)$
-bipartite-hole in
$(s,t)$
-bipartite-hole in
![]() $G$
consists of two disjoint sets
$G$
consists of two disjoint sets
![]() $S,\, T\subseteq V(G)$
with
$S,\, T\subseteq V(G)$
with
![]() $\vert S \vert =s$
and
$\vert S \vert =s$
and
![]() $\vert T \vert =t$
such that
$\vert T \vert =t$
such that
![]() $e_{G}(S,T)=0$
. The bipartite-hole number
$e_{G}(S,T)=0$
. The bipartite-hole number
![]() $\widetilde{\alpha }(G)$
refers to the maximum integer
$\widetilde{\alpha }(G)$
refers to the maximum integer
![]() $r$
such that
$r$
such that
![]() $G$
contains an
$G$
contains an
![]() $(s,t)$
-bipartite-hole for every pair of nonnegative integers
$(s,t)$
-bipartite-hole for every pair of nonnegative integers
![]() $s$
and
$s$
and
![]() $t$
with
$t$
with
![]() $s+t=r$
. In this paper, we adopt a slightly different notion of bipartite-hole number due to Nenadov and Pehova [Reference Nenadov and Pehova35].
$s+t=r$
. In this paper, we adopt a slightly different notion of bipartite-hole number due to Nenadov and Pehova [Reference Nenadov and Pehova35].
Definition 1.1. The bipartite independence number
![]() $\alpha ^*(G)$
is the maximum integer
$\alpha ^*(G)$
is the maximum integer
![]() $t$
such that
$t$
such that
![]() $G$
contains a
$G$
contains a
![]() $(t,t)$
-bipartite-hole.
$(t,t)$
-bipartite-hole.
It is clear from the definition that
![]() $2\alpha ^*(G)+1\geq \widetilde{\alpha }(G)\geq \alpha ^*(G)+1$
. McDiarmid and Yolov [Reference Mcdiarmid and Yolov33] showed that
$2\alpha ^*(G)+1\geq \widetilde{\alpha }(G)\geq \alpha ^*(G)+1$
. McDiarmid and Yolov [Reference Mcdiarmid and Yolov33] showed that
![]() $\delta (G)\ge \widetilde{\alpha }(G)$
is enough to force
$\delta (G)\ge \widetilde{\alpha }(G)$
is enough to force
![]() $G$
to be Hamiltonian and the minimum degree condition is sharp. Moreover, this was recently strengthened by Draganić, Correia, and Sudakov to the pancyclicity result [Reference Draganić, Correia and Sudakov8]. Also, Kim et al. [Reference Kim, Kim and Liu21] studied the decomposition of an almost regular graph
$G$
to be Hamiltonian and the minimum degree condition is sharp. Moreover, this was recently strengthened by Draganić, Correia, and Sudakov to the pancyclicity result [Reference Draganić, Correia and Sudakov8]. Also, Kim et al. [Reference Kim, Kim and Liu21] studied the decomposition of an almost regular graph
![]() $G$
with
$G$
with
![]() $\alpha ^*(G)=o(n)$
into almost spanning trees of bounded maximum degree.
$\alpha ^*(G)=o(n)$
into almost spanning trees of bounded maximum degree.
The main result of this paper is the following. We denote by
![]() $\mathcal{T}(n,\Delta )$
the family of all trees on
$\mathcal{T}(n,\Delta )$
the family of all trees on
![]() $n$
vertices with maximum degree at most
$n$
vertices with maximum degree at most
![]() $\Delta$
.
$\Delta$
.
Theorem 1.2.
For each
![]() $ \varepsilon \gt 0$
and
$ \varepsilon \gt 0$
and
![]() $\Delta \in \mathbb{N}$
, there exists
$\Delta \in \mathbb{N}$
, there exists
![]() $\alpha =\alpha (\varepsilon,\Delta )\gt 0$
such that the following holds for sufficiently large
$\alpha =\alpha (\varepsilon,\Delta )\gt 0$
such that the following holds for sufficiently large
![]() $n \in \mathbb{N}$
. Every
$n \in \mathbb{N}$
. Every
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G$
with
$G$
with
![]() $\delta (G)\ge \varepsilon n$
and
$\delta (G)\ge \varepsilon n$
and
![]() $\alpha ^*(G)\lt \alpha n$
is
$\alpha ^*(G)\lt \alpha n$
is
![]() $\mathcal{T}(n,\Delta )$
-universal, that is,
$\mathcal{T}(n,\Delta )$
-universal, that is,
![]() $G$
contains every
$G$
contains every
![]() $T\in \mathcal{T}(n,\Delta )$
as a subgraph.
$T\in \mathcal{T}(n,\Delta )$
as a subgraph.
That is, for a graph
![]() $G$
with sublinear
$G$
with sublinear
![]() $\alpha ^*(G)$
, the minimum degree condition forcing bounded-degree spanning trees is almost sublinear. We remark that the maximum degree
$\alpha ^*(G)$
, the minimum degree condition forcing bounded-degree spanning trees is almost sublinear. We remark that the maximum degree
![]() $\Delta$
of the tree in Theorem 1.2 cannot be larger than
$\Delta$
of the tree in Theorem 1.2 cannot be larger than
![]() $C\sqrt{n}$
for some constant
$C\sqrt{n}$
for some constant
![]() $C=C_{\alpha }\gt 0$
(in contrast to, for example, the result of [Reference Komlós, Sárközy and Szemerédi25], which holds for trees of maximum degree
$C=C_{\alpha }\gt 0$
(in contrast to, for example, the result of [Reference Komlós, Sárközy and Szemerédi25], which holds for trees of maximum degree
![]() $O(\frac{n}{\log n})$
) by the following construction. Given any
$O(\frac{n}{\log n})$
) by the following construction. Given any
![]() $\alpha \gt 0$
, choose positive integers
$\alpha \gt 0$
, choose positive integers
![]() $n, k, \Delta, d$
such that
$n, k, \Delta, d$
such that
![]() $k,\Delta$
are odd,
$k,\Delta$
are odd,
![]() $n=\Delta k-k+2$
,
$n=\Delta k-k+2$
,
![]() $\Delta \gt (k+2)d$
and
$\Delta \gt (k+2)d$
and
![]() $\frac{1}{d}\ll \alpha$
. It is easy to see that
$\frac{1}{d}\ll \alpha$
. It is easy to see that
![]() $\Delta \gt \sqrt{dn}$
. Let
$\Delta \gt \sqrt{dn}$
. Let
![]() $T$
be a caterpillar which consists of a path
$T$
be a caterpillar which consists of a path
![]() $P=v_1v_2\ldots v_k$
with
$P=v_1v_2\ldots v_k$
with
![]() $\Delta -1$
leaves attached to
$\Delta -1$
leaves attached to
![]() $v_i$
for each
$v_i$
for each
![]() $i\in \{1,k\}$
and
$i\in \{1,k\}$
and
![]() $\Delta -2$
leaves attached to
$\Delta -2$
leaves attached to
![]() $v_j$
for each
$v_j$
for each
![]() $j\in [2,k-1]$
. Now we are going to construct a graph
$j\in [2,k-1]$
. Now we are going to construct a graph
![]() $G$
with
$G$
with
![]() $\delta (G)=\frac{n}{2}+d-1$
and
$\delta (G)=\frac{n}{2}+d-1$
and
![]() $\alpha ^*(G)\le \alpha n$
, but that does not contain
$\alpha ^*(G)\le \alpha n$
, but that does not contain
![]() $T$
as a subgraph. Let
$T$
as a subgraph. Let
![]() $G_0=(V,E)$
be an
$G_0=(V,E)$
be an
![]() $(\frac{n}{2},d,\lambda )$
-regular graph such that
$(\frac{n}{2},d,\lambda )$
-regular graph such that
![]() $\lambda \le \alpha d$
, whose existence is guaranteed by a result of Friedman [Reference Friedman11] on random
$\lambda \le \alpha d$
, whose existence is guaranteed by a result of Friedman [Reference Friedman11] on random
![]() $d$
-regular graphs. Then we take two identical copies
$d$
-regular graphs. Then we take two identical copies
![]() $V_1$
and
$V_1$
and
![]() $V_2$
of
$V_2$
of
![]() $V$
, and join
$V$
, and join
![]() $u\in V_1$
and
$u\in V_1$
and
![]() $v\in V_2$
if
$v\in V_2$
if
![]() $uv\in E(G_0)$
. The resulting bipartite
$uv\in E(G_0)$
. The resulting bipartite
![]() $d$
-regular graph is denoted by
$d$
-regular graph is denoted by
![]() $G^*$
. Note that by the well-known Expander Mixing Lemma (applied to
$G^*$
. Note that by the well-known Expander Mixing Lemma (applied to
![]() $G_0$
), we have that for any
$G_0$
), we have that for any
![]() $A\subseteq V_1,B\subseteq V_2$
each of size
$A\subseteq V_1,B\subseteq V_2$
each of size
![]() $\alpha n$
,
$\alpha n$
,
We further add two disjoint copies of
![]() $K_{n/2}$
on
$K_{n/2}$
on
![]() $V_1$
,
$V_1$
,
![]() $V_2$
and call the resulting graph
$V_2$
and call the resulting graph
![]() $G$
. Thus we have
$G$
. Thus we have
![]() $\alpha ^*(G)\le \alpha n$
. Suppose
$\alpha ^*(G)\le \alpha n$
. Suppose
![]() $G$
contains a copy of
$G$
contains a copy of
![]() $T$
and
$T$
and
![]() $V_1$
has at least
$V_1$
has at least
![]() $\frac{k+1}{2}$
vertices of
$\frac{k+1}{2}$
vertices of
![]() $P$
since
$P$
since
![]() $k$
is odd. Indeed, whenever we embed a branch vertex
$k$
is odd. Indeed, whenever we embed a branch vertex
![]() $v_i\in V(P)$
into
$v_i\in V(P)$
into
![]() $V_1$
, we have to embed at least
$V_1$
, we have to embed at least
![]() $\Delta -2-d$
leaves, which are attached to
$\Delta -2-d$
leaves, which are attached to
![]() $v_i$
, into
$v_i$
, into
![]() $V_1$
as well. Thus the order of
$V_1$
as well. Thus the order of
![]() $V_1$
is at least
$V_1$
is at least
as
![]() $\Delta \gt (k+2)d$
, a contradiction.
$\Delta \gt (k+2)d$
, a contradiction.
Another motivation of our result is its connection to the randomly perturbed graphs introduced by Bohman et al. [Reference Bohman, Frieze and Martin2], where the host graph is obtained by adding random edges to a deterministic graph with minimum degree conditions. Krivelevich et al. [Reference Krivelevich, Kwan and Sudakov28] showed that for any
![]() $\varepsilon \gt 0$
,
$\varepsilon \gt 0$
,
![]() $\Delta \in \mathbb{N}$
and
$\Delta \in \mathbb{N}$
and
![]() $T\in \mathcal{T}(n,\Delta )$
, if
$T\in \mathcal{T}(n,\Delta )$
, if
![]() $G$
is an
$G$
is an
![]() $n$
-vertex graph with
$n$
-vertex graph with
![]() $\delta (G)\geq \varepsilon n$
, then the randomly perturbed graph
$\delta (G)\geq \varepsilon n$
, then the randomly perturbed graph
![]() $G\cup G(n,\frac{C}{n})$
a.a.s. contains
$G\cup G(n,\frac{C}{n})$
a.a.s. contains
![]() $T$
as a subgraph, where
$T$
as a subgraph, where
![]() $C$
depends only on
$C$
depends only on
![]() $\varepsilon$
and
$\varepsilon$
and
![]() $\Delta$
. They suggested that such a result can be improved to a universality result, that is,
$\Delta$
. They suggested that such a result can be improved to a universality result, that is,
![]() $G\cup G(n,\frac{C}{n})$
a.a.s. contains all members of
$G\cup G(n,\frac{C}{n})$
a.a.s. contains all members of
![]() $\mathcal{T}(n,\Delta )$
simultaneously. This is confirmed by Böttcher et al. [Reference Böttcher, Han, Kohayakawa, Montgomery, Parczyk and Person3]. Indeed, in their technical result which we state below, they replaced
$\mathcal{T}(n,\Delta )$
simultaneously. This is confirmed by Böttcher et al. [Reference Böttcher, Han, Kohayakawa, Montgomery, Parczyk and Person3]. Indeed, in their technical result which we state below, they replaced
![]() $G(n,\frac{C}{n})$
by a deterministic sparse expander graph, and thus get the universality part for free.
$G(n,\frac{C}{n})$
by a deterministic sparse expander graph, and thus get the universality part for free.
Theorem 1.3 ([Reference Böttcher, Han, Kohayakawa, Montgomery, Parczyk and Person3], Theorem 2). For any
![]() $\varepsilon \gt 0$
and integers
$\varepsilon \gt 0$
and integers
![]() $C\ge 2$
and
$C\ge 2$
and
![]() $\Delta \gt 1$
, there exist
$\Delta \gt 1$
, there exist
![]() $\alpha \gt 0$
,
$\alpha \gt 0$
,
![]() $D_0$
and
$D_0$
and
![]() $n_0$
such that the following holds for any
$n_0$
such that the following holds for any
![]() $D\ge D_0$
and
$D\ge D_0$
and
![]() $n\ge n_0$
. Let
$n\ge n_0$
. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph satisfying the following two conditions:
$n$
-vertex graph satisfying the following two conditions:
-
1.
 $\Delta (G)\leq CD$
,
$\Delta (G)\leq CD$
, -
2.
 $e(U, W)\ge \frac{D}{Cn}|U||W|$
for all sets
$e(U, W)\ge \frac{D}{Cn}|U||W|$
for all sets
 $U, W\subseteq V(G)$
with
$U, W\subseteq V(G)$
with
 $|U|,|W|\ge \alpha n$
.
$|U|,|W|\ge \alpha n$
.
Suppose
![]() $G_\varepsilon$
is an
$G_\varepsilon$
is an
![]() $n$
-vertex graph on the same vertex set and
$n$
-vertex graph on the same vertex set and
![]() $\delta (G_\varepsilon )\ge \varepsilon n$
. Then
$\delta (G_\varepsilon )\ge \varepsilon n$
. Then
![]() $H\;:\!=\;G_\varepsilon \cup G$
is
$H\;:\!=\;G_\varepsilon \cup G$
is
![]() $\mathcal{T}(n,\Delta )$
-universal.
$\mathcal{T}(n,\Delta )$
-universal.
Note that the graph
![]() $H$
in Theorem 1.3 satisfies
$H$
in Theorem 1.3 satisfies
![]() $\alpha ^*(H)\leq \alpha ^*(G)\lt \alpha n$
and
$\alpha ^*(H)\leq \alpha ^*(G)\lt \alpha n$
and
![]() $\delta (H)\ge \delta (G_\varepsilon )\ge \varepsilon n$
, so
$\delta (H)\ge \delta (G_\varepsilon )\ge \varepsilon n$
, so
![]() $H$
is
$H$
is
![]() $\mathcal{T}(n,\Delta )$
-universal by Theorem 1.2. Hence Theorem 1.2 slightly improves upon Theorem 1.3, where we do not need to distinguish two graphs (or equivalently the maximum degree condition on the sparse graph
$\mathcal{T}(n,\Delta )$
-universal by Theorem 1.2. Hence Theorem 1.2 slightly improves upon Theorem 1.3, where we do not need to distinguish two graphs (or equivalently the maximum degree condition on the sparse graph
![]() $G$
is no longer needed).
$G$
is no longer needed).
2. Proof strategy and preliminaries
2.1. Notation
For a graph
![]() $G=(V,E)$
, let
$G=(V,E)$
, let
![]() $v(G)=\vert V\vert$
and
$v(G)=\vert V\vert$
and
![]() $e(G)=\vert E\vert$
. Given a collection of subgraphs
$e(G)=\vert E\vert$
. Given a collection of subgraphs
![]() $\mathcal{F}=\left \{ F_{i}\;:\; i\in I\right \}$
, let
$\mathcal{F}=\left \{ F_{i}\;:\; i\in I\right \}$
, let
![]() $V(\mathcal{F})=\cup _{i\in I}V(F_{i})$
. Given two vertex-disjoint graphs
$V(\mathcal{F})=\cup _{i\in I}V(F_{i})$
. Given two vertex-disjoint graphs
![]() $G_1, G_2$
, let
$G_1, G_2$
, let
![]() $G_1\cup G_2$
be the union of
$G_1\cup G_2$
be the union of
![]() $G_1$
and
$G_1$
and
![]() $G_2$
. For
$G_2$
. For
![]() $U \subseteq V(G)$
, let
$U \subseteq V(G)$
, let
![]() $G[U]$
be the induced subgraph of
$G[U]$
be the induced subgraph of
![]() $G$
on
$G$
on
![]() $U$
and let
$U$
and let
![]() $G-U$
be the induced graph after removing
$G-U$
be the induced graph after removing
![]() $U$
, that is
$U$
, that is
![]() $G-U\;:\!=\;G[V\backslash U]$
. Given a vertex
$G-U\;:\!=\;G[V\backslash U]$
. Given a vertex
![]() $v\in V(G)$
and
$v\in V(G)$
and
![]() $X,Y\subseteq V(G)$
, denoted by
$X,Y\subseteq V(G)$
, denoted by
![]() $N_{X}(v)$
the set of neighbours of
$N_{X}(v)$
the set of neighbours of
![]() $v$
in
$v$
in
![]() $X$
and let
$X$
and let
![]() $d_{X}(v)\;:\!=\;\vert N_{X}(v)\vert$
. The neighbourhood of
$d_{X}(v)\;:\!=\;\vert N_{X}(v)\vert$
. The neighbourhood of
![]() $X$
in
$X$
in
![]() $G$
is denoted by
$G$
is denoted by
![]() $N_{G}(X)=(\cup _{v\in X}N(v))\backslash X$
and let
$N_{G}(X)=(\cup _{v\in X}N(v))\backslash X$
and let
![]() $N_{Y}(X)=N_{G}(X)\cap Y$
. We omit the index
$N_{Y}(X)=N_{G}(X)\cap Y$
. We omit the index
![]() $G$
if the graph is clear from the context.
$G$
if the graph is clear from the context.
For a graph
![]() $F$
on
$F$
on
![]() $[k]\;:\!=\;\left \{ 1,\ldots,k\right \}$
, we say that
$[k]\;:\!=\;\left \{ 1,\ldots,k\right \}$
, we say that
![]() $B$
is the
$B$
is the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $F$
if there exists a partition
$F$
if there exists a partition
![]() $V_{1},\ldots,V_{k}$
of
$V_{1},\ldots,V_{k}$
of
![]() $V(B)$
such that
$V(B)$
such that
![]() $\vert V_{1}\vert =\cdots =\vert V_{k} \vert =n$
and we have that
$\vert V_{1}\vert =\cdots =\vert V_{k} \vert =n$
and we have that
![]() $\{u,v\}\in E(B)$
if and only if
$\{u,v\}\in E(B)$
if and only if
![]() $u\in V_{i}$
and
$u\in V_{i}$
and
![]() $v\in V_{j}$
for some
$v\in V_{j}$
for some
![]() $\{i,j\}\in E(F)$
. Given a spanning subgraph
$\{i,j\}\in E(F)$
. Given a spanning subgraph
![]() $G$
of
$G$
of
![]() $B$
, we call the sequence
$B$
, we call the sequence
![]() $V_1,\dots, V_k$
the parts of
$V_1,\dots, V_k$
the parts of
![]() $G$
and we define
$G$
and we define
![]() $\bar{\delta }(G)\;:\!=\;\min _{\{i,j\}\in E(F)}\delta (G[V_i,V_{j}])$
where
$\bar{\delta }(G)\;:\!=\;\min _{\{i,j\}\in E(F)}\delta (G[V_i,V_{j}])$
where
![]() $G[V_i,V_{j}]$
is the bipartite subgraph of
$G[V_i,V_{j}]$
is the bipartite subgraph of
![]() $G$
induced by the parts
$G$
induced by the parts
![]() $V_i$
and
$V_i$
and
![]() $V_{j}$
. A subset
$V_{j}$
. A subset
![]() $R$
of
$R$
of
![]() $V(G)$
is balanced if
$V(G)$
is balanced if
![]() $\vert R\cap V_1\vert =\cdots =\vert R\cap V_k\vert$
. In particular, we say a subset of
$\vert R\cap V_1\vert =\cdots =\vert R\cap V_k\vert$
. In particular, we say a subset of
![]() $V(G)$
or a subgraph of
$V(G)$
or a subgraph of
![]() $G$
transversal if it intersects each part in exactly one vertex.
$G$
transversal if it intersects each part in exactly one vertex.
For a path
![]() $P$
, the length of
$P$
, the length of
![]() $P$
is the number of edges in
$P$
is the number of edges in
![]() $P$
. Given two vertices
$P$
. Given two vertices
![]() $x,y$
, an
$x,y$
, an
![]() $x,y$
-path is a path with ends
$x,y$
-path is a path with ends
![]() $x$
and
$x$
and
![]() $y$
. Let
$y$
. Let
![]() $T$
be a tree and
$T$
be a tree and
![]() $T^{\prime }$
be obtained from
$T^{\prime }$
be obtained from
![]() $T$
by removing all leaves. A pendant star is a maximal star centred at a leaf of
$T$
by removing all leaves. A pendant star is a maximal star centred at a leaf of
![]() $T^{\prime }$
, where the unique neighbour of the centre inside
$T^{\prime }$
, where the unique neighbour of the centre inside
![]() $T^{\prime }$
is called the root of the pendant star. A bare path in
$T^{\prime }$
is called the root of the pendant star. A bare path in
![]() $T$
is a path whose internal vertices have degree exactly two in
$T$
is a path whose internal vertices have degree exactly two in
![]() $T$
. A caterpillar in
$T$
. A caterpillar in
![]() $T$
consists of a bare path in
$T$
consists of a bare path in
![]() $T^{\prime }$
as the central path with some (possibly empty) leaves attached to the internal vertices of the central path, where branch vertices are the internal vertices attached with at least one leaf. The length and ends of the caterpillar refer to the length and ends of its central path.
$T^{\prime }$
as the central path with some (possibly empty) leaves attached to the internal vertices of the central path, where branch vertices are the internal vertices attached with at least one leaf. The length and ends of the caterpillar refer to the length and ends of its central path.
For two graphs
![]() $H$
and
$H$
and
![]() $G$
, an embedding
$G$
, an embedding
![]() $\varphi$
of
$\varphi$
of
![]() $H$
in
$H$
in
![]() $G$
is an injective map
$G$
is an injective map
![]() $\varphi \;:\; V(H) \rightarrow V(G)$
such that
$\varphi \;:\; V(H) \rightarrow V(G)$
such that
![]() $\left \{ v,w \right \}\in E(H)$
implies
$\left \{ v,w \right \}\in E(H)$
implies
![]() $\left \{ \varphi (v),\varphi (w) \right \} \in E(G)$
. For all integers
$\left \{ \varphi (v),\varphi (w) \right \} \in E(G)$
. For all integers
![]() $a, b$
with
$a, b$
with
![]() $a\leq b$
, let
$a\leq b$
, let
![]() $[a,b]\;:\!=\; \left \{ i\in \mathbb{Z}\;:\;a\leq i \leq b \right \}$
and
$[a,b]\;:\!=\; \left \{ i\in \mathbb{Z}\;:\;a\leq i \leq b \right \}$
and
![]() $[a]\;:\!=\;\left \{ 1, 2,\dots, a \right \}$
. When we write
$[a]\;:\!=\;\left \{ 1, 2,\dots, a \right \}$
. When we write
![]() $\alpha \ll \beta \ll \gamma$
, we always mean that
$\alpha \ll \beta \ll \gamma$
, we always mean that
![]() $\alpha, \beta, \gamma$
are constants in
$\alpha, \beta, \gamma$
are constants in
![]() $(0, 1)$
, and
$(0, 1)$
, and
![]() $\beta \ll \gamma$
means that there exists
$\beta \ll \gamma$
means that there exists
![]() $\beta _{0}=\beta _{0}(\gamma )$
such that the subsequent arguments hold for all
$\beta _{0}=\beta _{0}(\gamma )$
such that the subsequent arguments hold for all
![]() $0\lt \beta \leq \beta _{0}$
. Hierarchies of other lengths are defined analogously. For the sake of clarity of presentation, we will sometimes omit floor and ceiling signs when they are not crucial.
$0\lt \beta \leq \beta _{0}$
. Hierarchies of other lengths are defined analogously. For the sake of clarity of presentation, we will sometimes omit floor and ceiling signs when they are not crucial.
2.2. Graph expansion and trees
We will introduce some graph expansion properties to embed the trees.
Definition 2.1 ([Reference Johannsen, Krivelevich and Samotij18]). Let
![]() $n \in \mathbb{N}$
and
$n \in \mathbb{N}$
and
![]() $d\gt 0$
. A graph
$d\gt 0$
. A graph
![]() $G$
is an
$G$
is an
![]() $(n,d)$
-expander if
$(n,d)$
-expander if
![]() $\vert G \vert =n$
and
$\vert G \vert =n$
and
![]() $G$
satisfies the following two conditions.
$G$
satisfies the following two conditions.
-
1.
 $\vert N_{G} (X)\vert \geq d\vert X \vert$
for all sets
$\vert N_{G} (X)\vert \geq d\vert X \vert$
for all sets
 $X \subseteq V(G)$
with
$X \subseteq V(G)$
with
 $1\leq \vert X \vert \lt \lceil \frac{n}{2d} \rceil$
.
$1\leq \vert X \vert \lt \lceil \frac{n}{2d} \rceil$
. -
2.
 $e_{G}(X,Y)\gt 0$
for all disjoint
$e_{G}(X,Y)\gt 0$
for all disjoint
 $X,Y \subseteq V(G)$
with
$X,Y \subseteq V(G)$
with
 $\vert X \vert =\vert Y \vert =\lceil \frac{n}{2d} \rceil$
.
$\vert X \vert =\vert Y \vert =\lceil \frac{n}{2d} \rceil$
.
In [Reference Krivelevich27], Krivelevich considered trees differently according to whether they contain many leaves or many disjoint bare paths.
Lemma 2.2 ([Reference Krivelevich27]). For any integers
![]() $n,k\gt 2$
, a tree on
$n,k\gt 2$
, a tree on
![]() $n$
vertices either has at least
$n$
vertices either has at least
![]() $\frac{n}{4k}$
leaves or a collection of at least
$\frac{n}{4k}$
leaves or a collection of at least
![]() $\frac{n}{4k}$
vertex-disjoint bare paths of length
$\frac{n}{4k}$
vertex-disjoint bare paths of length
![]() $k$
.
$k$
.
We will use the following corollary to divide
![]() $\mathcal{T}(n,\Delta )$
into trees with many pendant stars and trees with many vertex-disjoint caterpillars.
$\mathcal{T}(n,\Delta )$
into trees with many pendant stars and trees with many vertex-disjoint caterpillars.
Corollary 2.3.
For any integer
![]() $n,k\gt 2$
, a tree on
$n,k\gt 2$
, a tree on
![]() $n$
vertices with maximum degree
$n$
vertices with maximum degree
![]() $\Delta$
either has at least
$\Delta$
either has at least
![]() $\frac{n}{4k\Delta }$
pendant stars or a collection of at least
$\frac{n}{4k\Delta }$
pendant stars or a collection of at least
![]() $\frac{n}{4k\Delta }$
vertex-disjoint caterpillars each of length
$\frac{n}{4k\Delta }$
vertex-disjoint caterpillars each of length
![]() $k$
.
$k$
.
Suppose
![]() $T$
is an
$T$
is an
![]() $n$
-vertex tree with maximum degree at most
$n$
-vertex tree with maximum degree at most
![]() $\Delta$
and
$\Delta$
and
![]() $T^{\prime }$
is the subtree obtained by removing all leaves. Then it holds that
$T^{\prime }$
is the subtree obtained by removing all leaves. Then it holds that
![]() $\vert T^{\prime } \vert +\vert T^{\prime } \vert (\Delta -1)\geq n$
. We can apply Lemma 2.2 on
$\vert T^{\prime } \vert +\vert T^{\prime } \vert (\Delta -1)\geq n$
. We can apply Lemma 2.2 on
![]() $T^{\prime }$
to obtain at least
$T^{\prime }$
to obtain at least
![]() $\frac{|T^\prime |}{4k}\ge \frac{n}{4k\Delta }$
pendant stars or a collection of at least
$\frac{|T^\prime |}{4k}\ge \frac{n}{4k\Delta }$
pendant stars or a collection of at least
![]() $\frac{n}{4k\Delta }$
vertex-disjoint caterpillars of length
$\frac{n}{4k\Delta }$
vertex-disjoint caterpillars of length
![]() $k$
in
$k$
in
![]() $T$
.
$T$
.
In [Reference Haxell16], Haxell extended a result of Friedman and Pippenger [Reference Friedman and Pippenger12] and showed that one can embed every almost spanning tree with bounded maximum degree in a graph with strong expansion property. We will use the following result by Johannsen et al. [Reference Johannsen, Krivelevich and Samotij18].
Theorem 2.4 ([Reference Johannsen, Krivelevich and Samotij18]). Let
![]() $n,\Delta \in \mathbb{N}$
,
$n,\Delta \in \mathbb{N}$
,
![]() $d \in \mathbb{R}^+$
with
$d \in \mathbb{R}^+$
with
![]() $d \geq 2\Delta$
and
$d \geq 2\Delta$
and
![]() $G$
be an
$G$
be an
![]() $(n,d)$
-expander. Given any
$(n,d)$
-expander. Given any
![]() $T \in \mathcal{T}(n-4\Delta \lceil \frac{n}{2d} \rceil, \Delta )$
, we can find a copy of
$T \in \mathcal{T}(n-4\Delta \lceil \frac{n}{2d} \rceil, \Delta )$
, we can find a copy of
![]() $T$
in
$T$
in
![]() $G$
.
$G$
.
As shown by Johannsen et al. [Reference Johannsen, Krivelevich and Samotij18], the following lemma is useful for attaching leaves onto certain vertices.
Definition 2.5 ([Reference Johannsen, Krivelevich and Samotij18]). Given a bipartite graph
![]() $G=(A,B,E)$
with
$G=(A,B,E)$
with
![]() $\vert A\vert \leq \vert B\vert$
and a function
$\vert A\vert \leq \vert B\vert$
and a function
![]() $f\;:\; A\rightarrow \mathbb{N}$
with
$f\;:\; A\rightarrow \mathbb{N}$
with
![]() $\sum _{u\in A}f(u) = |B|$
, an
$\sum _{u\in A}f(u) = |B|$
, an
![]() $f$
-matching from
$f$
-matching from
![]() $A$
into
$A$
into
![]() $B$
is a collection of vertex-disjoint stars
$B$
is a collection of vertex-disjoint stars
![]() $\{S_u\;:\;u\in A\}$
in
$\{S_u\;:\;u\in A\}$
in
![]() $G$
such that
$G$
such that
![]() $S_u$
has
$S_u$
has
![]() $u$
as the centre and exactly
$u$
as the centre and exactly
![]() $f(u)$
leaves inside
$f(u)$
leaves inside
![]() $B$
.
$B$
.
Lemma 2.6 ([Reference Johannsen, Krivelevich and Samotij18]). Let
![]() $d,m\in \mathbb{N}$
and let
$d,m\in \mathbb{N}$
and let
![]() $G$
be a graph. Suppose that two disjoint sets
$G$
be a graph. Suppose that two disjoint sets
![]() $U,W \subseteq V(G)$
satisfy the following three conditions:
$U,W \subseteq V(G)$
satisfy the following three conditions:
-
1.
 $\vert N_{G} (X) \cap W\vert \geq d\vert X \vert$
for all sets
$\vert N_{G} (X) \cap W\vert \geq d\vert X \vert$
for all sets
 $X \subseteq U$
with
$X \subseteq U$
with
 $1\leq \vert X \vert \leq m$
,
$1\leq \vert X \vert \leq m$
, -
2.
 $e_{G}(X,Y)\gt 0$
for all
$e_{G}(X,Y)\gt 0$
for all
 $X \subseteq U$
and
$X \subseteq U$
and
 $Y\subseteq W$
with
$Y\subseteq W$
with
 $\vert X \vert =\vert Y \vert \geq m$
,
$\vert X \vert =\vert Y \vert \geq m$
, -
3.
 $d_U(w) \geq m$
for all
$d_U(w) \geq m$
for all
 $w \in W$
.
$w \in W$
.
Then for every
![]() $f\;:\; U\to \{1,\dots,d\}$
with
$f\;:\; U\to \{1,\dots,d\}$
with
![]() $\sum _{u\in U}f(u)=\vert W\vert$
, there exists an
$\sum _{u\in U}f(u)=\vert W\vert$
, there exists an
![]() $f$
-matching from
$f$
-matching from
![]() $U$
into
$U$
into
![]() $W$
.
$W$
.
2.3. Proof overview
We give a brief outline of our proof here. Similar to previous works [Reference Krivelevich27, Reference Krivelevich, Kwan and Sudakov28, Reference Montgomery34], we classify the trees and deal with them separately. Our classification is given in Corollary 2.3, which refines Lemma 2.2. First, for the pendant star case, let
![]() $T_1$
be a subtree obtained by deleting the centres and leaves of pendant stars in
$T_1$
be a subtree obtained by deleting the centres and leaves of pendant stars in
![]() $T$
(but not the roots). We randomly partition
$T$
(but not the roots). We randomly partition
![]() $V(G)$
into
$V(G)$
into
![]() $V_{1}, V_{2}$
and
$V_{1}, V_{2}$
and
![]() $V_{3}$
and embed
$V_{3}$
and embed
![]() $T_1$
into
$T_1$
into
![]() $G[V_{1}]$
by Theorem 2.4. Then we greedily embed most of the centres into
$G[V_{1}]$
by Theorem 2.4. Then we greedily embed most of the centres into
![]() $V_{2}$
. The
$V_{2}$
. The
![]() $\alpha ^*$
property guarantees that we are left with a small portion of centres and we shall embed them by the degree condition into
$\alpha ^*$
property guarantees that we are left with a small portion of centres and we shall embed them by the degree condition into
![]() $V_{3}$
. Finally we use Lemma 2.6 to find a desired star-matching and complete the embedding.
$V_{3}$
. Finally we use Lemma 2.6 to find a desired star-matching and complete the embedding.
For the caterpillar case, we shall embed a suitable subset of branch vertices into a random set with “good” expansion properties. In this way, we can greedily finish the last step of embedding leaves of caterpillars by a star-matching. To embed this suitable branch vertex set, we control the length of the caterpillars and let
![]() $T_2$
be the subforest obtained by deleting these caterpillars except the ends. First, we randomly partition
$T_2$
be the subforest obtained by deleting these caterpillars except the ends. First, we randomly partition
![]() $V(G)$
into
$V(G)$
into
![]() $V_1,V_2$
, and
$V_1,V_2$
, and
![]() $V_3$
, and embed
$V_3$
, and embed
![]() $T_2$
into
$T_2$
into
![]() $V_1$
as the above case. To embed central paths of these caterpillars, we randomly partition
$V_1$
as the above case. To embed central paths of these caterpillars, we randomly partition
![]() $V_2$
set into
$V_2$
set into
![]() $k-1$
equal parts
$k-1$
equal parts
![]() $X_1,\dots,X_{k-1}$
, where
$X_1,\dots,X_{k-1}$
, where
![]() $k$
is the length of the caterpillars. Then we define an auxiliary graph
$k$
is the length of the caterpillars. Then we define an auxiliary graph
![]() $H$
with
$H$
with
![]() $V(H)=X'_{1}\cup X'_2\cup \cdots \cup X'_{k-2}$
which is a spanning subgraph of the blow-up of
$V(H)=X'_{1}\cup X'_2\cup \cdots \cup X'_{k-2}$
which is a spanning subgraph of the blow-up of
![]() $C_{k-2}$
and
$C_{k-2}$
and
![]() $X'_i$
is roughly the same as
$X'_i$
is roughly the same as
![]() $X_i$
. In this way, we transform the problem of embedding vertex-disjoint central paths into finding a transversal cycle-factor in
$X_i$
. In this way, we transform the problem of embedding vertex-disjoint central paths into finding a transversal cycle-factor in
![]() $H$
, as Lemma 2.7 below. Once central paths have been embedded, we can greedily embed leaves of caterpillars by a star-matching as mentioned above and complete the embedding. Now we state Lemma 2.7. Let
$H$
, as Lemma 2.7 below. Once central paths have been embedded, we can greedily embed leaves of caterpillars by a star-matching as mentioned above and complete the embedding. Now we state Lemma 2.7. Let
![]() $G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
$G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_k$
and let
$C_k$
and let
![]() $\alpha ^*_{\textrm{b}}(G)$
be the largest integer
$\alpha ^*_{\textrm{b}}(G)$
be the largest integer
![]() $s$
such that
$s$
such that
![]() $G=(V_{1},\ldots,V_{k},E)$
contains an
$G=(V_{1},\ldots,V_{k},E)$
contains an
![]() $(s,s)$
-bipartite-hole
$(s,s)$
-bipartite-hole
![]() $(S,T)$
where
$(S,T)$
where
![]() $S\subseteq V_i, T\subseteq V_{i+1}$
for some
$S\subseteq V_i, T\subseteq V_{i+1}$
for some
![]() $i\in [k]$
.
$i\in [k]$
.
Lemma 2.7.
Given a positive integer
![]() $k \in 4\mathbb{N}$
and a constant
$k \in 4\mathbb{N}$
and a constant
![]() $\delta$
with
$\delta$
with
![]() $\delta \gt \frac{2}{k}$
, there exists
$\delta \gt \frac{2}{k}$
, there exists
![]() $\alpha \gt 0$
such that the following holds for sufficiently large
$\alpha \gt 0$
such that the following holds for sufficiently large
![]() $n \in \mathbb{N}$
. Let
$n \in \mathbb{N}$
. Let
![]() $G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the n-blow-up of
$G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the n-blow-up of
![]() $C_{k}$
with
$C_{k}$
with
![]() $\bar{\delta }(G)\geq \delta n$
and
$\bar{\delta }(G)\geq \delta n$
and
![]() $\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
. Then
$\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
. Then
![]() $G$
has a transversal
$G$
has a transversal
![]() $C_{k}$
-factor.
$C_{k}$
-factor.
Although the minimum degree bound in Lemma 2.7 is not best possible and it only works for
![]() $k \in 4\mathbb{N}$
, but it is enough for our purpose (indeed, we only need it work for large
$k \in 4\mathbb{N}$
, but it is enough for our purpose (indeed, we only need it work for large
![]() $k$
). We suspect that the (asymptotic) tight condition should be
$k$
). We suspect that the (asymptotic) tight condition should be
![]() $(1+o(1))\frac nk$
, given by the so-called space barrier. Indeed, let
$(1+o(1))\frac nk$
, given by the so-called space barrier. Indeed, let
![]() $G$
be a (complete)
$G$
be a (complete)
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_k$
with parts labelled as
$C_k$
with parts labelled as
![]() $V_{1},\ldots,V_{k}$
. One can specify a set
$V_{1},\ldots,V_{k}$
. One can specify a set
![]() $U_i$
of size
$U_i$
of size
![]() $n/k-1$
in each cluster
$n/k-1$
in each cluster
![]() $V_i$
,
$V_i$
,
![]() $i\in [k]$
and remove all edges not touching
$i\in [k]$
and remove all edges not touching
![]() $U\;:\!=\;\bigcup _{i\in [k]} U_i$
from
$U\;:\!=\;\bigcup _{i\in [k]} U_i$
from
![]() $G$
. Then we add a
$G$
. Then we add a
![]() $k$
-partite Erdős graph (obtained from random graph) to
$k$
-partite Erdős graph (obtained from random graph) to
![]() $V(G)\setminus U$
so that the resulting graph
$V(G)\setminus U$
so that the resulting graph
![]() $G'$
satisfy
$G'$
satisfy
![]() $\alpha ^*_{\textrm{b}}(G')=o( n)$
but
$\alpha ^*_{\textrm{b}}(G')=o( n)$
but
![]() $G^\prime -U$
is
$G^\prime -U$
is
![]() $C_k$
-free. Now every transversal copy of
$C_k$
-free. Now every transversal copy of
![]() $C_k$
in
$C_k$
in
![]() $G'$
must contain a vertex in
$G'$
must contain a vertex in
![]() $U$
and
$U$
and
![]() $\bar{\delta }(G')\geq n/k-1$
. Since
$\bar{\delta }(G')\geq n/k-1$
. Since
![]() $|U|\lt n$
,
$|U|\lt n$
,
![]() $G'$
does not have a transversal
$G'$
does not have a transversal
![]() $C_{k}$
-factor.
$C_{k}$
-factor.
If we remove the
![]() $\alpha ^*_{\textrm{b}}$
condition in Lemma 2.7, then the minimum degree threshold for transversal
$\alpha ^*_{\textrm{b}}$
condition in Lemma 2.7, then the minimum degree threshold for transversal
![]() $C_{k}$
-factor is asymptotically
$C_{k}$
-factor is asymptotically
![]() $\bar{\delta }(G)\geq (1+\frac 1k)\frac n2+o(n)$
, as determined recently by Ergemlidze and Molla in [Reference Ergemlidze and Molla9].
$\bar{\delta }(G)\geq (1+\frac 1k)\frac n2+o(n)$
, as determined recently by Ergemlidze and Molla in [Reference Ergemlidze and Molla9].
Our proof of Lemma 2.7 is based on the absorption method, which will be given in Section 4.4. Finally, there are some other minimum degree-type results in blown-up graphs [Reference Ergemlidze and Molla9, Reference Johansson19] and in multi-partite graphs [Reference Fischer10, Reference Keevash and Mycroft20, Reference Lo and Markström29, Reference Magyar and Martin31, Reference Martin and Szemerédi32], but not with any randomness condition.
3. Proof of the main theorem
Proof of Theorem
1.2. Given a positive integer
![]() $\Delta$
and a constant
$\Delta$
and a constant
![]() $\varepsilon \gt 0$
, we set
$\varepsilon \gt 0$
, we set
![]() $k=48\lceil \frac{1}{\varepsilon } \rceil$
,
$k=48\lceil \frac{1}{\varepsilon } \rceil$
,
![]() $\gamma =\frac{1}{4k\Delta ^2}$
and
$\gamma =\frac{1}{4k\Delta ^2}$
and
![]() $\eta =\frac{1}{4k\Delta }$
. Choose
$\eta =\frac{1}{4k\Delta }$
. Choose
and let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph with
$n$
-vertex graph with
![]() $\delta (G)\ge \varepsilon n$
and
$\delta (G)\ge \varepsilon n$
and
![]() $\alpha ^*(G)\lt \alpha n$
. Given any tree
$\alpha ^*(G)\lt \alpha n$
. Given any tree
![]() $T\in \mathcal{T}(n,\Delta )$
, by Corollary 2.3, we proceed the proof by considering the following two cases.
$T\in \mathcal{T}(n,\Delta )$
, by Corollary 2.3, we proceed the proof by considering the following two cases.
Case 1.
![]() $T$
has at least
$T$
has at least
![]() $\eta n$
pendant stars.
$\eta n$
pendant stars.
We can easily pick a collection of
![]() $\gamma n$
vertex-disjoint pendant stars in
$\gamma n$
vertex-disjoint pendant stars in
![]() $T$
and label it as
$T$
and label it as
![]() $\mathcal{D}=\{D_1,\dots,D_{\gamma n}\}$
for convenience. Write
$\mathcal{D}=\{D_1,\dots,D_{\gamma n}\}$
for convenience. Write
![]() $A\;:\!=\;\left \{ a_{1},\dots,a_{\gamma n} \right \}$
and
$A\;:\!=\;\left \{ a_{1},\dots,a_{\gamma n} \right \}$
and
![]() $B\;:\!=\;\left \{ b_{1},\dots,b_{\gamma n} \right \}$
where
$B\;:\!=\;\left \{ b_{1},\dots,b_{\gamma n} \right \}$
where
![]() $a_{i}$
and
$a_{i}$
and
![]() $b_{i}$
are the root and centre of
$b_{i}$
are the root and centre of
![]() $D_i$
, respectively. Let
$D_i$
, respectively. Let
![]() $\mathcal{S}=\left \{ S_{1},\dots,S_{\gamma n} \right \}$
where each
$\mathcal{S}=\left \{ S_{1},\dots,S_{\gamma n} \right \}$
where each
![]() $S_{i}$
is obtained from
$S_{i}$
is obtained from
![]() $D_i$
by removing the root. Let
$D_i$
by removing the root. Let
![]() $T_{1}$
be a subtree of
$T_{1}$
be a subtree of
![]() $T$
obtained by deleting vertices of
$T$
obtained by deleting vertices of
![]() $\mathcal{S}$
. Note that
$\mathcal{S}$
. Note that
![]() $\vert T_{1}\vert \leq n-2\gamma n$
. Moreover we claim that
$\vert T_{1}\vert \leq n-2\gamma n$
. Moreover we claim that
![]() $V(G)$
can be partitioned into
$V(G)$
can be partitioned into
![]() $V_{1},V_{2},V_{3}$
of sizes
$V_{1},V_{2},V_{3}$
of sizes
![]() $n_{1},n_{2},n_{3}$
, respectively, such that
$n_{1},n_{2},n_{3}$
, respectively, such that
where
Choose a partition
![]() $\left \{ V_{1},V_{2},V_{3} \right \}$
of
$\left \{ V_{1},V_{2},V_{3} \right \}$
of
![]() $V(G)$
uniformly at random where
$V(G)$
uniformly at random where
![]() $\vert V_{i} \vert =n_{i}$
. For every
$\vert V_{i} \vert =n_{i}$
. For every
![]() $v\in V(G)$
, let
$v\in V(G)$
, let
![]() $f^{i}_{v}=d_{V_i}(v)$
and note that
$f^{i}_{v}=d_{V_i}(v)$
and note that
![]() $\mu _{v}^{i}\;:\!=\;\mathbb{E}[f_{v}^{i}]\geq \varepsilon n_{i}$
. Let
$\mu _{v}^{i}\;:\!=\;\mathbb{E}[f_{v}^{i}]\geq \varepsilon n_{i}$
. Let
![]() $q$
be the probability that there exist
$q$
be the probability that there exist
![]() $v\in V(G)$
and
$v\in V(G)$
and
![]() $i\in [3]$
which violates property (1). Then by the union bound and Chernoff’s inequality (see e.g. [Reference Janson, Łuczak and Ruciński17], Theorem 2.1),
$i\in [3]$
which violates property (1). Then by the union bound and Chernoff’s inequality (see e.g. [Reference Janson, Łuczak and Ruciński17], Theorem 2.1),
for sufficiently large
![]() $n$
. Therefore, with positive probability the randomly chosen partition
$n$
. Therefore, with positive probability the randomly chosen partition
![]() $\left \{ V_{1},V_{2},V_{3} \right \}$
satisfies property (1). Then we have
$\left \{ V_{1},V_{2},V_{3} \right \}$
satisfies property (1). Then we have
 \begin{align} n_{3}&\geq n-\gamma n-\frac{d(n-2\gamma n)+4\Delta d}{d-2\Delta }=\frac{(d+2\Delta )\gamma n-2\Delta n-4\Delta d}{d-2\Delta } \nonumber \\ &\geq \frac{d\gamma n-2\Delta n}{2d}\geq \frac{\gamma n}{4} \geq \frac{6\Delta \alpha n}{\varepsilon }, \end{align}
\begin{align} n_{3}&\geq n-\gamma n-\frac{d(n-2\gamma n)+4\Delta d}{d-2\Delta }=\frac{(d+2\Delta )\gamma n-2\Delta n-4\Delta d}{d-2\Delta } \nonumber \\ &\geq \frac{d\gamma n-2\Delta n}{2d}\geq \frac{\gamma n}{4} \geq \frac{6\Delta \alpha n}{\varepsilon }, \end{align}
where in the penultimate inequality we use
![]() $d\gamma n-2\Delta n\geq \frac{d\gamma n}{2}$
because
$d\gamma n-2\Delta n\geq \frac{d\gamma n}{2}$
because
![]() $\frac{1}{d}\ll \varepsilon,\frac{1}{\Delta }$
and the last inequality follows since
$\frac{1}{d}\ll \varepsilon,\frac{1}{\Delta }$
and the last inequality follows since
![]() $\alpha \ll \varepsilon,\frac{1}{\Delta }$
.
$\alpha \ll \varepsilon,\frac{1}{\Delta }$
.
Claim 3.1.
![]() $G[V_{1}]$
is an
$G[V_{1}]$
is an
![]() $(n_1,d)$
-expander.
$(n_1,d)$
-expander.
Proof. Let
![]() $m_{1}=\lceil \frac{\vert V_{1}\vert }{2d}\rceil$
and
$m_{1}=\lceil \frac{\vert V_{1}\vert }{2d}\rceil$
and
![]() $m_{2}=\lceil \frac{\varepsilon \vert V_{1}\vert }{2d+2} \rceil$
. Since
$m_{2}=\lceil \frac{\varepsilon \vert V_{1}\vert }{2d+2} \rceil$
. Since
![]() $\alpha ^*(G)\lt \alpha n \leq m_{1}$
, there is at least one edge between any two vertex-disjoint sets of size
$\alpha ^*(G)\lt \alpha n \leq m_{1}$
, there is at least one edge between any two vertex-disjoint sets of size
![]() $m_1$
in
$m_1$
in
![]() $G[V_{1}]$
. For
$G[V_{1}]$
. For
![]() $X \subseteq V_{1}$
with
$X \subseteq V_{1}$
with
![]() $1\le \vert X\vert \le m_{2}$
, by (1), we have
$1\le \vert X\vert \le m_{2}$
, by (1), we have
For
![]() $X\subseteq V_{1}$
with
$X\subseteq V_{1}$
with
![]() $m_{2}\lt \vert X\vert \lt m_{1}$
, since
$m_{2}\lt \vert X\vert \lt m_{1}$
, since
![]() $\alpha \ll \frac{1}{d}$
,
$\alpha \ll \frac{1}{d}$
,
![]() $ \varepsilon$
, we can arbitrarily pick
$ \varepsilon$
, we can arbitrarily pick
![]() $Z\subseteq X$
with
$Z\subseteq X$
with
![]() $\vert Z\vert =\alpha n$
. As there is no edge between
$\vert Z\vert =\alpha n$
. As there is no edge between
![]() $Z$
and
$Z$
and
![]() $V_{1}\backslash (Z\cup N_{V_{1}}(Z))$
, we have
$V_{1}\backslash (Z\cup N_{V_{1}}(Z))$
, we have
![]() $\vert V_{1}\backslash (Z\cup N_{V_{1}}(Z))\vert \lt \alpha n$
, then
$\vert V_{1}\backslash (Z\cup N_{V_{1}}(Z))\vert \lt \alpha n$
, then
![]() $\vert N_{V_{1}}(Z)\vert \gt \vert V_{1}\vert -2\alpha n$
. Thus
$\vert N_{V_{1}}(Z)\vert \gt \vert V_{1}\vert -2\alpha n$
. Thus
Together with (4),
![]() $G[V_{1}]$
is an
$G[V_{1}]$
is an
![]() $(n_1,d)$
-expander.
$(n_1,d)$
-expander.
Note that
![]() $\vert T_{1}\vert = n_{1}-4\Delta (\frac{n_{1}}{2d}+1) \leq n_{1}-4\Delta \lceil \frac{n_{1}}{2d} \rceil$
, where the first equality follows since
$\vert T_{1}\vert = n_{1}-4\Delta (\frac{n_{1}}{2d}+1) \leq n_{1}-4\Delta \lceil \frac{n_{1}}{2d} \rceil$
, where the first equality follows since
![]() $n_{1}= \frac{d\vert T_{1}\vert +4\Delta d}{d-2\Delta }$
. Then by Theorem 2.4, there exists an embedding
$n_{1}= \frac{d\vert T_{1}\vert +4\Delta d}{d-2\Delta }$
. Then by Theorem 2.4, there exists an embedding
![]() $f_{1}\;:\;V(T_1)\to V_1$
. Let
$f_{1}\;:\;V(T_1)\to V_1$
. Let
![]() $L_{0}=V_{1}\backslash f_{1}(T_{1})$
and
$L_{0}=V_{1}\backslash f_{1}(T_{1})$
and
![]() $L_{1}= f_{1}(A)$
. Next, we will embed the centres of pendant stars into
$L_{1}= f_{1}(A)$
. Next, we will embed the centres of pendant stars into
![]() $V_{2} \cup V_{3}$
and we do it in two steps.
$V_{2} \cup V_{3}$
and we do it in two steps.
In the first step, we embed most of the vertices of
![]() $B$
into
$B$
into
![]() $V_{2}$
. Consider the bipartite graph
$V_{2}$
. Consider the bipartite graph
![]() $H$
on vertex sets
$H$
on vertex sets
![]() $L_{1}$
and
$L_{1}$
and
![]() $V_{2}$
, where
$V_{2}$
, where
![]() $\vert L_{1} \vert =\vert V_{2}\vert =\gamma n$
. Let
$\vert L_{1} \vert =\vert V_{2}\vert =\gamma n$
. Let
![]() $M$
be a maximum matching in
$M$
be a maximum matching in
![]() $H$
and we claim that
$H$
and we claim that
![]() $\vert E(M)\vert \geq \gamma n-\alpha n$
. Otherwise, since
$\vert E(M)\vert \geq \gamma n-\alpha n$
. Otherwise, since
![]() $\alpha ^*(G)\lt \alpha n$
, there is at least one edge in
$\alpha ^*(G)\lt \alpha n$
, there is at least one edge in
![]() $H-V(M)$
, contrary to the maximality of
$H-V(M)$
, contrary to the maximality of
![]() $M$
. Let
$M$
. Let
![]() $L_2=V(M)\cap V_2$
and
$L_2=V(M)\cap V_2$
and
![]() $L_{3}=V_{2}\setminus L_{2}$
. Without loss of generality, suppose we have embedded
$L_{3}=V_{2}\setminus L_{2}$
. Without loss of generality, suppose we have embedded
![]() $B_{1}=\left \{ b_{1},\dots,b_{t}\right \}$
into
$B_{1}=\left \{ b_{1},\dots,b_{t}\right \}$
into
![]() $L_2$
, where
$L_2$
, where
![]() $t\geq \gamma n-\alpha n$
.
$t\geq \gamma n-\alpha n$
.
In the second step, we shall embed the vertices of
![]() $B\setminus B_{1}$
into
$B\setminus B_{1}$
into
![]() $V_{3}$
. For every
$V_{3}$
. For every
![]() $u\in V(G)$
, by (1) and (3), we have
$u\in V(G)$
, by (1) and (3), we have
![]() $d_{V_{3}}(u)\geq \frac{\varepsilon }{2}\vert V_{3} \vert \geq \Delta \alpha n$
. Hence we can greedily embed
$d_{V_{3}}(u)\geq \frac{\varepsilon }{2}\vert V_{3} \vert \geq \Delta \alpha n$
. Hence we can greedily embed
![]() $S_{t+1},\dots,S_{ \gamma n}$
into
$S_{t+1},\dots,S_{ \gamma n}$
into
![]() $G[V_{3}]$
. Let
$G[V_{3}]$
. Let
![]() $\mathcal{S}_1=\{S_1,\dots,S_t\}$
. It follows that there exists an embedding
$\mathcal{S}_1=\{S_1,\dots,S_t\}$
. It follows that there exists an embedding
![]() $f_{2}\;:\; V(B_{1})\cup V(\mathcal{S}\setminus \mathcal{S}_{1})\rightarrow V_{2}\cup V_{3}$
such that
$f_{2}\;:\; V(B_{1})\cup V(\mathcal{S}\setminus \mathcal{S}_{1})\rightarrow V_{2}\cup V_{3}$
such that
![]() $f_{2}(B_{1})=L_{2}$
and
$f_{2}(B_{1})=L_{2}$
and
![]() $f_{2}(\mathcal{S}\setminus \mathcal{S}_{1})\subseteq V_{3}$
. Let
$f_{2}(\mathcal{S}\setminus \mathcal{S}_{1})\subseteq V_{3}$
. Let
![]() $L_{4}=V_{3}\setminus f_{2}(\mathcal{S}\setminus \mathcal{S}_{1})$
and we have
$L_{4}=V_{3}\setminus f_{2}(\mathcal{S}\setminus \mathcal{S}_{1})$
and we have
![]() $\vert L_{4} \vert \geq \vert V_{3}\vert -\Delta \alpha n$
.
$\vert L_{4} \vert \geq \vert V_{3}\vert -\Delta \alpha n$
.
Now it remains to embed the leaves attached to the vertices of
![]() $ B_{1}$
. Consider the bipartite graph
$ B_{1}$
. Consider the bipartite graph
![]() $Q$
on vertex sets
$Q$
on vertex sets
![]() $L_{2}$
and
$L_{2}$
and
![]() $L$
, where
$L$
, where
![]() $L=L_{0}\cup L_{3}\cup L_{4}$
. Let
$L=L_{0}\cup L_{3}\cup L_{4}$
. Let
![]() $m\;:\!=\;2\alpha n$
and
$m\;:\!=\;2\alpha n$
and
![]() $d\;:\!=\;\Delta -1$
. Since
$d\;:\!=\;\Delta -1$
. Since
![]() $\alpha ^*(G)\lt \alpha n\lt m$
, there is at least one edge between any two disjoint vertex set of size
$\alpha ^*(G)\lt \alpha n\lt m$
, there is at least one edge between any two disjoint vertex set of size
![]() $m$
in
$m$
in
![]() $Q$
. For all
$Q$
. For all
![]() $X\subseteq L_{2}$
with
$X\subseteq L_{2}$
with
![]() $1\leq \vert X\vert \leq m$
, by (1) and (3), we have
$1\leq \vert X\vert \leq m$
, by (1) and (3), we have
![]() $\vert N_{Q}(X)\cap L\vert \geq \vert N_{Q}(X)\cap L_{4}\vert \geq \frac{\varepsilon }{2}\vert V_{3} \vert -\Delta \alpha n\geq d\vert X \vert$
. Moreover for each
$\vert N_{Q}(X)\cap L\vert \geq \vert N_{Q}(X)\cap L_{4}\vert \geq \frac{\varepsilon }{2}\vert V_{3} \vert -\Delta \alpha n\geq d\vert X \vert$
. Moreover for each
![]() $u \in L$
, we have
$u \in L$
, we have
![]() $d_{ L_{2}}(u)\geq \frac{\varepsilon }{2}\vert V_{2} \vert -\alpha n\geq m$
due to
$d_{ L_{2}}(u)\geq \frac{\varepsilon }{2}\vert V_{2} \vert -\alpha n\geq m$
due to
![]() $\alpha \ll \varepsilon,\frac{1}{\Delta }$
. Therefore by applying Lemma 2.6 on
$\alpha \ll \varepsilon,\frac{1}{\Delta }$
. Therefore by applying Lemma 2.6 on
![]() $Q$
, we obtain an embedding
$Q$
, we obtain an embedding
![]() $f_{3}$
of
$f_{3}$
of
![]() $\mathcal{S}_{1}$
in
$\mathcal{S}_{1}$
in
![]() $Q$
such that
$Q$
such that
![]() $f_{3}(u)=f_{2}(u)$
for every
$f_{3}(u)=f_{2}(u)$
for every
![]() $u\in B_{1}$
. In conclusion, it is clear that the map
$u\in B_{1}$
. In conclusion, it is clear that the map
![]() $f\;:\; V(T)\rightarrow V(G)$
defined by
$f\;:\; V(T)\rightarrow V(G)$
defined by
 \begin{equation*} f(u)\;:\!=\;\left \{ \begin{array}{l@{\quad}l} f_{1}(u)& \textrm{if}\; u\in V(T_{1}) \\ f_{2}(u) &\textrm{if}\; u\in V(\mathcal{S})\setminus V(\mathcal{S}_{1}) \\ f_{3}(u) &\textrm{if}\; u\in V(\mathcal{S}_{1}) \\ \end{array} \right . \end{equation*}
\begin{equation*} f(u)\;:\!=\;\left \{ \begin{array}{l@{\quad}l} f_{1}(u)& \textrm{if}\; u\in V(T_{1}) \\ f_{2}(u) &\textrm{if}\; u\in V(\mathcal{S})\setminus V(\mathcal{S}_{1}) \\ f_{3}(u) &\textrm{if}\; u\in V(\mathcal{S}_{1}) \\ \end{array} \right . \end{equation*}
is an embedding of
![]() $T$
in
$T$
in
![]() $G$
. The proof of Case 1 is complete.
$G$
. The proof of Case 1 is complete.
Case 2.
![]() $T$
has at least
$T$
has at least
![]() $\eta n$
vertex-disjoint caterpillars of length
$\eta n$
vertex-disjoint caterpillars of length
![]() $k$
.
$k$
.
A caterpillar in
![]() $T$
consists of a bare path in
$T$
consists of a bare path in
![]() $T^{\prime }$
as the central path with some (possibly empty) leaves attached to the internal vertices of the central path, where
$T^{\prime }$
as the central path with some (possibly empty) leaves attached to the internal vertices of the central path, where
![]() $T^\prime$
is the subtree obtained by deleting the leaves of
$T^\prime$
is the subtree obtained by deleting the leaves of
![]() $T$
and we say that the internal vertices attached with leaves are branch vertices. Observe that
$T$
and we say that the internal vertices attached with leaves are branch vertices. Observe that
![]() $T$
either has a family of at least
$T$
either has a family of at least
![]() $\frac{\eta n}{2}$
caterpillars of length
$\frac{\eta n}{2}$
caterpillars of length
![]() $k$
that have at least one leaf or a family of at least
$k$
that have at least one leaf or a family of at least
![]() $\frac{\eta n}{2}$
bare paths of length
$\frac{\eta n}{2}$
bare paths of length
![]() $k$
. Here, we will give a detailed proof for the first subcase and the second subcase can be derived by the same argument.
$k$
. Here, we will give a detailed proof for the first subcase and the second subcase can be derived by the same argument.
Let
![]() $n^{\prime }=\frac{\eta n}{2}$
and
$n^{\prime }=\frac{\eta n}{2}$
and
![]() $k^{\prime }$
be an integer from
$k^{\prime }$
be an integer from
![]() $\{ \frac{k}{2}, \frac{k}{2}-1, \frac{k}{2}-2, \frac{k}{2}-3\}$
such that
$\{ \frac{k}{2}, \frac{k}{2}-1, \frac{k}{2}-2, \frac{k}{2}-3\}$
such that
![]() $k^{\prime }=2$
(mod 4). It is easy to pick a collection of
$k^{\prime }=2$
(mod 4). It is easy to pick a collection of
![]() $n^{\prime }$
vertex-disjoint caterpillars of length
$n^{\prime }$
vertex-disjoint caterpillars of length
![]() $k^{\prime }$
in
$k^{\prime }$
in
![]() $T$
such that one end of each caterpillar is adjacent to a branch vertex in
$T$
such that one end of each caterpillar is adjacent to a branch vertex in
![]() $T$
. Let
$T$
. Let
![]() $\mathcal{F}=\left \{ F_{1},\dots,F_{n^{\prime }} \right \}$
be such a collection and
$\mathcal{F}=\left \{ F_{1},\dots,F_{n^{\prime }} \right \}$
be such a collection and
![]() $\mathcal{P}=\left \{ P_{1},\dots,P_{n^{\prime }} \right \}$
, where each
$\mathcal{P}=\left \{ P_{1},\dots,P_{n^{\prime }} \right \}$
, where each
![]() $P_{i}$
is the central path of
$P_{i}$
is the central path of
![]() $F_{i}$
. Write
$F_{i}$
. Write
![]() $S\;:\!=\;\left \{ s_{1},\dots,s_{n^{\prime }}\right \}$
and
$S\;:\!=\;\left \{ s_{1},\dots,s_{n^{\prime }}\right \}$
and
![]() $W\;:\!=\;\left \{ w_{1},\dots,w_{n^{\prime }}\right \}$
where
$W\;:\!=\;\left \{ w_{1},\dots,w_{n^{\prime }}\right \}$
where
![]() $s_{i}$
and
$s_{i}$
and
![]() $w_{i}$
are the ends of
$w_{i}$
are the ends of
![]() $F_{i}$
and assume that the neighbour of
$F_{i}$
and assume that the neighbour of
![]() $s_i$
in
$s_i$
in
![]() $P_i$
is a branch vertex,
$P_i$
is a branch vertex,
![]() $i\in [n^{\prime }]$
.
$i\in [n^{\prime }]$
.
Let
![]() $T_{2}$
be a subforest of
$T_{2}$
be a subforest of
![]() $T$
obtained by deleting the vertices of
$T$
obtained by deleting the vertices of
![]() $\mathcal{F}$
except the ends of every caterpillar and note that
$\mathcal{F}$
except the ends of every caterpillar and note that
![]() $ \vert T_2\vert \leq n-n^\prime k^\prime$
. In a similar way as Case 1, there exists a partition
$ \vert T_2\vert \leq n-n^\prime k^\prime$
. In a similar way as Case 1, there exists a partition
![]() $\left \{ V_{1},V_{2},V_{3} \right \}$
of
$\left \{ V_{1},V_{2},V_{3} \right \}$
of
![]() $V(G)$
such that
$V(G)$
such that
where
Then we have
where the first inequality follows since
![]() $\vert T_2\vert \leq n-n^\prime k^\prime$
and the last inequality follows since
$\vert T_2\vert \leq n-n^\prime k^\prime$
and the last inequality follows since
![]() $\alpha \ll \varepsilon,\frac{1}{\Delta }$
.
$\alpha \ll \varepsilon,\frac{1}{\Delta }$
.
Note that
![]() $\vert T_{2} \vert = \vert V_{1}\vert -4\Delta (\frac{\vert V_{1}\vert }{2d}+1)\leq \vert V_{1}\vert -4\Delta \lceil \frac{\vert V_{1}\vert }{2d}\rceil$
, where the first equality follows since
$\vert T_{2} \vert = \vert V_{1}\vert -4\Delta (\frac{\vert V_{1}\vert }{2d}+1)\leq \vert V_{1}\vert -4\Delta \lceil \frac{\vert V_{1}\vert }{2d}\rceil$
, where the first equality follows since
![]() $\vert V_{1}\vert =\vert T_{2} \vert + \frac{2\Delta \vert T_{2}\vert +4\Delta d}{d-2\Delta }$
. Then Theorem 2.4 implies that there exists an embedding
$\vert V_{1}\vert =\vert T_{2} \vert + \frac{2\Delta \vert T_{2}\vert +4\Delta d}{d-2\Delta }$
. Then Theorem 2.4 implies that there exists an embedding
![]() $g_1$
of
$g_1$
of
![]() $T_{2}$
in
$T_{2}$
in
![]() $G[V_{1}]$
. Let
$G[V_{1}]$
. Let
![]() $L_{1}=V_{1}\backslash g_{1}(T_{2})$
and
$L_{1}=V_{1}\backslash g_{1}(T_{2})$
and
![]() $V_{2}^{\prime }=V_2\cup L_1$
. It now remains to embed
$V_{2}^{\prime }=V_2\cup L_1$
. It now remains to embed
![]() $n^{\prime }$
caterpillars in
$n^{\prime }$
caterpillars in
![]() $\mathcal{F}$
.
$\mathcal{F}$
.
First, we shall embed the internal vertices of
![]() $\mathcal{P}$
into
$\mathcal{P}$
into
![]() $V_{2}^{\prime }$
. Randomly partition
$V_{2}^{\prime }$
. Randomly partition
![]() $V_2^{\prime }$
into
$V_2^{\prime }$
into
![]() $X_1,\dots,X_{k^{\prime }-1}$
each of size
$X_1,\dots,X_{k^{\prime }-1}$
each of size
![]() $n^{\prime }$
. The union bound and Chernoff’s inequality imply that, if
$n^{\prime }$
. The union bound and Chernoff’s inequality imply that, if
![]() $n$
is sufficiently large, then there exists a partition such that for every
$n$
is sufficiently large, then there exists a partition such that for every
![]() $u\in V(G)$
and
$u\in V(G)$
and
![]() $i\in [k^\prime -1]$
, we have
$i\in [k^\prime -1]$
, we have
![]() $d_{X_i}(u)\ge \frac{\varepsilon n^{\prime }}{4}$
. Since
$d_{X_i}(u)\ge \frac{\varepsilon n^{\prime }}{4}$
. Since
![]() $\alpha ^*(G)\lt \alpha n\leq n^{\prime }$
, there exists a matching
$\alpha ^*(G)\lt \alpha n\leq n^{\prime }$
, there exists a matching
![]() $M_{1}$
between
$M_{1}$
between
![]() $g_{1}(S)$
and
$g_{1}(S)$
and
![]() $X_{1}$
such that
$X_{1}$
such that
![]() $t_1\;:\!=\;\vert E(M_{1})\vert \gt n^{\prime }-\alpha n$
. Similarly, there exists a matching
$t_1\;:\!=\;\vert E(M_{1})\vert \gt n^{\prime }-\alpha n$
. Similarly, there exists a matching
![]() $M_{2}$
between
$M_{2}$
between
![]() $g_1(W)$
and
$g_1(W)$
and
![]() $X_{k^{\prime }-1}$
such that
$X_{k^{\prime }-1}$
such that
![]() $t_2\;:\!=\;\vert E(M_{2})\vert \gt n^{\prime }-\alpha n$
. Let
$t_2\;:\!=\;\vert E(M_{2})\vert \gt n^{\prime }-\alpha n$
. Let
![]() $S_1=\{s_1,\dots,s_{t_1}\}\subseteq S$
and
$S_1=\{s_1,\dots,s_{t_1}\}\subseteq S$
and
![]() $W_1=\{w_1,\dots,w_{t_2}\}\subseteq W$
. Without loss of generality, we assume that
$W_1=\{w_1,\dots,w_{t_2}\}\subseteq W$
. Without loss of generality, we assume that
![]() $g_1(S_1)\subseteq V(M_{1})$
and
$g_1(S_1)\subseteq V(M_{1})$
and
![]() $g_1(W_1)\subseteq V(M_{2})$
. By the choice of
$g_1(W_1)\subseteq V(M_{2})$
. By the choice of
![]() $X_1,\dots, X_{k^\prime -1}$
, for each
$X_1,\dots, X_{k^\prime -1}$
, for each
![]() $u\in g_1((S\cup W)G^\prime -Us (S_{1}\cup W_1))\subseteq V(G)$
, we have
$u\in g_1((S\cup W)G^\prime -Us (S_{1}\cup W_1))\subseteq V(G)$
, we have
Therefore we can greedily find a matching
![]() $M_3$
between
$M_3$
between
![]() $g_1(S\setminus S_{1})$
and
$g_1(S\setminus S_{1})$
and
![]() $X_2$
covering
$X_2$
covering
![]() $g_1(S\setminus S_{1})$
, and a matching
$g_1(S\setminus S_{1})$
, and a matching
![]() $M_4$
between
$M_4$
between
![]() $g_1(W\setminus W_{1})$
and
$g_1(W\setminus W_{1})$
and
![]() $X_2$
covering
$X_2$
covering
![]() $g_1(W\setminus W_{1})$
, where
$g_1(W\setminus W_{1})$
, where
![]() $V(M_3)\cap V(M_4)=\emptyset$
. Let
$V(M_3)\cap V(M_4)=\emptyset$
. Let
![]() $X_1^\prime \;:\!=\;(V(M_1)\cap X_1)\cup (V(M_3)\cap X_2)$
,
$X_1^\prime \;:\!=\;(V(M_1)\cap X_1)\cup (V(M_3)\cap X_2)$
,
![]() $X_{k^\prime -1}^\prime \;:\!=\;(V(M_2)\cap X_{k^\prime -1})\cup (V(M_4)\cap X_2)$
,
$X_{k^\prime -1}^\prime \;:\!=\;(V(M_2)\cap X_{k^\prime -1})\cup (V(M_4)\cap X_2)$
,
![]() $X_2^\prime \;:\!=\;(X_2 \setminus (V(M_3)\cup V(M_4))) \cup (X_1\setminus V(M_1))\cup (X_{k^\prime -1}\setminus V(M_2))$
and let
$X_2^\prime \;:\!=\;(X_2 \setminus (V(M_3)\cup V(M_4))) \cup (X_1\setminus V(M_1))\cup (X_{k^\prime -1}\setminus V(M_2))$
and let
![]() $X_i^\prime \;:\!=\;X_i$
for
$X_i^\prime \;:\!=\;X_i$
for
![]() $i\in [3,k^\prime -2]$
. In this way, we obtain a new partition
$i\in [3,k^\prime -2]$
. In this way, we obtain a new partition
![]() $\left \{ X_{1}^\prime,\dots,X^\prime _{k^\prime -1} \right \}$
of
$\left \{ X_{1}^\prime,\dots,X^\prime _{k^\prime -1} \right \}$
of
![]() $V_{2}^{\prime }$
such that there exist perfect matchings between
$V_{2}^{\prime }$
such that there exist perfect matchings between
![]() $X_1^\prime$
and
$X_1^\prime$
and
![]() $g_1(S)$
and between
$g_1(S)$
and between
![]() $X^\prime _{k^{\prime }-1}$
and
$X^\prime _{k^{\prime }-1}$
and
![]() $g_1(W)$
. Let
$g_1(W)$
. Let
![]() $X_{1}^\prime =\left \{ x_{1},\dots,x_{n^{\prime }}\right \}$
and
$X_{1}^\prime =\left \{ x_{1},\dots,x_{n^{\prime }}\right \}$
and
![]() $X^\prime _{k^{\prime }-1}=\left \{ y_{1},\dots,y_{n^{\prime }}\right \}$
where for each
$X^\prime _{k^{\prime }-1}=\left \{ y_{1},\dots,y_{n^{\prime }}\right \}$
where for each
![]() $i\in [n^{\prime }]$
,
$i\in [n^{\prime }]$
,
![]() $\{x_{i},g_1(s_{i})\}$
and
$\{x_{i},g_1(s_{i})\}$
and
![]() $\{y_{i},g_1(w_{i})\}$
are edges of the above perfect matchings.
$\{y_{i},g_1(w_{i})\}$
are edges of the above perfect matchings.
Let
![]() $X^\prime _{0}=\left \{ z_{1},\dots,z_{n^{\prime }}\right \}$
be a new set of vertices disjoint from
$X^\prime _{0}=\left \{ z_{1},\dots,z_{n^{\prime }}\right \}$
be a new set of vertices disjoint from
![]() $V(G)$
. Define an auxiliary graph
$V(G)$
. Define an auxiliary graph
![]() $H$
with vertex set
$H$
with vertex set
![]() $V(H)=X^\prime _{0}\cup X^\prime _{2}\cup \cdots \cup X^\prime _{k^{\prime }-2}$
. For
$V(H)=X^\prime _{0}\cup X^\prime _{2}\cup \cdots \cup X^\prime _{k^{\prime }-2}$
. For
![]() $2\leq i\leq k^{\prime }-3$
, the edges of
$2\leq i\leq k^{\prime }-3$
, the edges of
![]() $H$
between
$H$
between
![]() $X^\prime _{i}$
and
$X^\prime _{i}$
and
![]() $X^\prime _{i+1}$
are identical to those of
$X^\prime _{i+1}$
are identical to those of
![]() $G$
. For
$G$
. For
![]() $v\in X^\prime _{2}$
and
$v\in X^\prime _{2}$
and
![]() $z_{j}\in X^\prime _{0}$
,
$z_{j}\in X^\prime _{0}$
,
![]() $\left \{ v,z_{j}\right \}$
is an edge of
$\left \{ v,z_{j}\right \}$
is an edge of
![]() $H$
if and only if
$H$
if and only if
![]() $\left \{v,x_{j}\right \}$
is an edge of
$\left \{v,x_{j}\right \}$
is an edge of
![]() $G$
. Similarly, for
$G$
. Similarly, for
![]() $u\in X^\prime _{k^{\prime }-2}$
and
$u\in X^\prime _{k^{\prime }-2}$
and
![]() $z_{j}\in X^\prime _{0}$
,
$z_{j}\in X^\prime _{0}$
,
![]() $\left \{ u,z_{j}\right \}$
is an edge of
$\left \{ u,z_{j}\right \}$
is an edge of
![]() $H$
if and only if
$H$
if and only if
![]() $\left \{ u,y_{j}\right \}$
is an edge of
$\left \{ u,y_{j}\right \}$
is an edge of
![]() $G$
. Observe that if
$G$
. Observe that if
![]() $H$
has a transversal
$H$
has a transversal
![]() $C_{k^{\prime }-2}$
-factor, then
$C_{k^{\prime }-2}$
-factor, then
![]() $G$
has
$G$
has
![]() $n^{\prime }$
vertex-disjoint paths of length
$n^{\prime }$
vertex-disjoint paths of length
![]() $k^{\prime }-2$
that connect
$k^{\prime }-2$
that connect
![]() $x_{i}$
and
$x_{i}$
and
![]() $y_{i}$
. Since we moved at most
$y_{i}$
. Since we moved at most
![]() $2\alpha n$
vertices when we constructed the new partition, now we have that
$2\alpha n$
vertices when we constructed the new partition, now we have that
Then Lemma 2.7 implies that
![]() $H$
contains a transversal
$H$
contains a transversal
![]() $C_{k^{\prime }-2}$
-factor. Together with the perfect matchings, we find an embedding
$C_{k^{\prime }-2}$
-factor. Together with the perfect matchings, we find an embedding
![]() $g_2$
of
$g_2$
of
![]() $V(\mathcal{P})$
to
$V(\mathcal{P})$
to
![]() $V_2^{\prime }$
that connects
$V_2^{\prime }$
that connects
![]() $g_1(s_{i})$
and
$g_1(s_{i})$
and
![]() $g_1(w_{i})$
for each
$g_1(w_{i})$
for each
![]() $i\in [n^{\prime }]$
. Now it suffices to embed the leaves of caterpillars into
$i\in [n^{\prime }]$
. Now it suffices to embed the leaves of caterpillars into
![]() $V_{3}$
.
$V_{3}$
.
Let
![]() $I\subseteq V_2^{\prime }$
be the set of images of branch vertices in
$I\subseteq V_2^{\prime }$
be the set of images of branch vertices in
![]() $V(\mathcal{F})$
. Since every vertex in
$V(\mathcal{F})$
. Since every vertex in
![]() $S$
is adjacent to a branch vertex in
$S$
is adjacent to a branch vertex in
![]() $F_i$
, we have
$F_i$
, we have
![]() $X_{1}^\prime \subseteq I$
. Let
$X_{1}^\prime \subseteq I$
. Let
![]() $m\;:\!=\;\alpha n$
and
$m\;:\!=\;\alpha n$
and
![]() $d\;:\!=\;\Delta$
. For all
$d\;:\!=\;\Delta$
. For all
![]() $X\subseteq I$
with
$X\subseteq I$
with
![]() $1\leq \vert X\vert \leq m$
, by (6) and (8), we have
$1\leq \vert X\vert \leq m$
, by (6) and (8), we have
![]() $\vert N_{G}(X)\cap V_{3}\vert \geq \frac{\varepsilon }{2}\vert V_{3} \vert \geq d\vert X\vert$
. Moreover for each
$\vert N_{G}(X)\cap V_{3}\vert \geq \frac{\varepsilon }{2}\vert V_{3} \vert \geq d\vert X\vert$
. Moreover for each
![]() $u \in V_{3}$
, by (9), we have
$u \in V_{3}$
, by (9), we have
![]() $d_{I}(u) \geq d_{X^\prime _{1}}(u)\geq \frac{\varepsilon n^{\prime } }{8} \geq m$
. Together with the assumption that
$d_{I}(u) \geq d_{X^\prime _{1}}(u)\geq \frac{\varepsilon n^{\prime } }{8} \geq m$
. Together with the assumption that
![]() $\alpha ^*(G)\lt m$
, Lemma 2.6 implies that there exists an embedding
$\alpha ^*(G)\lt m$
, Lemma 2.6 implies that there exists an embedding
![]() $g_{3}$
of
$g_{3}$
of
![]() $V(\mathcal{F})\backslash V(\mathcal{P})$
to
$V(\mathcal{F})\backslash V(\mathcal{P})$
to
![]() $V_{3}$
that respects the edges between the branch vertices and the leaves of caterpillars. It follows that the map
$V_{3}$
that respects the edges between the branch vertices and the leaves of caterpillars. It follows that the map
![]() $g\;:\; V(T)\rightarrow V(G)$
defined by
$g\;:\; V(T)\rightarrow V(G)$
defined by
 \begin{equation*} g(u)\;:\!=\;\left \{ \begin{array}{l@{\quad}l} g_{1}(u)& \textrm{if}\; u\in V(T_{2}) \\ g_{2}(u) &\textrm{if}\; u\in V(\mathcal{P}) \\ g_{3}(u) &\textrm{if}\; u\in V(\mathcal{F})\backslash V(\mathcal{P}) \\ \end{array} \right . \end{equation*}
\begin{equation*} g(u)\;:\!=\;\left \{ \begin{array}{l@{\quad}l} g_{1}(u)& \textrm{if}\; u\in V(T_{2}) \\ g_{2}(u) &\textrm{if}\; u\in V(\mathcal{P}) \\ g_{3}(u) &\textrm{if}\; u\in V(\mathcal{F})\backslash V(\mathcal{P}) \\ \end{array} \right . \end{equation*}
is an embedding of
![]() $T$
in
$T$
in
![]() $G$
. This concludes the proof of the first subcase.
$G$
. This concludes the proof of the first subcase.
As for the second subcase, we adopt a similar argument and the main difference is that we split
![]() $V(G)$
into two parts because the caterpillars have no leaves and it suffices to find
$V(G)$
into two parts because the caterpillars have no leaves and it suffices to find
![]() $g_1$
and
$g_1$
and
![]() $g_2$
.
$g_2$
.
4. Transversal
 $C_{k}$
-factor
$C_{k}$
-factor
4.1. Proof of Lemma 2.7
Following the typical absorption method, the main tasks are to (
![]() $i$
) establish an absorbing set
$i$
) establish an absorbing set
![]() $R$
and (
$R$
and (
![]() $ii$
) find an almost perfect transversal
$ii$
) find an almost perfect transversal
![]() $C_{k}$
-tiling in
$C_{k}$
-tiling in
![]() $G-R$
. For (
$G-R$
. For (
![]() $i$
), we will introduce some related definitions.
$i$
), we will introduce some related definitions.
Definition 4.1. Let
![]() $G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
$G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_{k}$
and
$C_{k}$
and
![]() $F$
be a
$F$
be a
![]() $k$
-vertex graph.
$k$
-vertex graph.
-
1. We say that a balanced subset
 $R\subseteq V(G)$
is a
$R\subseteq V(G)$
is a
 $\xi$
-absorbing set for some
$\xi$
-absorbing set for some
 $\xi \gt 0$
if for every balanced subset
$\xi \gt 0$
if for every balanced subset
 $U\subseteq V(G)\backslash R$
with
$U\subseteq V(G)\backslash R$
with
 $\vert U\vert \leq \xi n$
,
$\vert U\vert \leq \xi n$
,
 $G[R\cup U]$
contains an
$G[R\cup U]$
contains an
 $F$
-factor which consists of transversal copies.
$F$
-factor which consists of transversal copies. -
2. Given a subset
 $S\subseteq V(G)$
of size
$S\subseteq V(G)$
of size
 $k$
and an integer
$k$
and an integer
 $t$
, we say that a subset
$t$
, we say that a subset
 $A_{S}\subseteq V(G) \backslash S$
is an
$A_{S}\subseteq V(G) \backslash S$
is an
 $(F,t)$
-absorber of
$(F,t)$
-absorber of
 $S$
if
$S$
if
 $\vert A_{S}\vert \leq kt$
and both
$\vert A_{S}\vert \leq kt$
and both
 $G[A_{S}]$
and
$G[A_{S}]$
and
 $G[A_{S}\cup S]$
contain an
$G[A_{S}\cup S]$
contain an
 $F$
-factor.
$F$
-factor.
Now we state the first crucial lemma, whose proof can be found in Section 4.4.2.
Lemma 4.2. (Absorbing Lemma). Given
![]() $k \in \mathbb{N}$
with
$k \in \mathbb{N}$
with
![]() $k\geq 4$
and positive constants
$k\geq 4$
and positive constants
![]() $\delta,\gamma$
with
$\delta,\gamma$
with
![]() $\delta \gt \frac{2}{k}$
and
$\delta \gt \frac{2}{k}$
and
![]() $\gamma \leq \frac{\delta }{2}$
, there exist
$\gamma \leq \frac{\delta }{2}$
, there exist
![]() $\alpha, \xi \gt 0$
such that the following holds for sufficiently large
$\alpha, \xi \gt 0$
such that the following holds for sufficiently large
![]() $n \in \mathbb{N}$
. Let
$n \in \mathbb{N}$
. Let
![]() $G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
$G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_{k}$
with
$C_{k}$
with
![]() $\bar{\delta }(G)\geq \delta n$
and
$\bar{\delta }(G)\geq \delta n$
and
![]() $\alpha ^*_{\mathrm{b}}(G)\lt \alpha n$
. Then there exists a
$\alpha ^*_{\mathrm{b}}(G)\lt \alpha n$
. Then there exists a
![]() $\xi$
-absorbing set
$\xi$
-absorbing set
![]() $R\subseteq V(G)$
of size at most
$R\subseteq V(G)$
of size at most
![]() $\gamma n$
.
$\gamma n$
.
For (
![]() $ii$
), Lemma 4.3 provides an almost transversal
$ii$
), Lemma 4.3 provides an almost transversal
![]() $C_{k}$
-tiling, whose proof will be given in Section 4.3.
$C_{k}$
-tiling, whose proof will be given in Section 4.3.
Lemma 4.3. (Almost perfect tiling). Given a positive integer
![]() $k\in 4\mathbb{N}$
and constants
$k\in 4\mathbb{N}$
and constants
![]() $\delta,\zeta$
with
$\delta,\zeta$
with
![]() $\delta \gt \frac{2}{k}$
, there exists
$\delta \gt \frac{2}{k}$
, there exists
![]() $\alpha \gt 0$
such that the following holds for sufficiently large
$\alpha \gt 0$
such that the following holds for sufficiently large
![]() $n \in \mathbb{N}$
. Let
$n \in \mathbb{N}$
. Let
![]() $G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the n-blow-up of
$G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the n-blow-up of
![]() $C_{k}$
with
$C_{k}$
with
![]() $\bar{\delta }(G)\geq \delta n$
and
$\bar{\delta }(G)\geq \delta n$
and
![]() $\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
. Then
$\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
. Then
![]() $G$
contains a transversal
$G$
contains a transversal
![]() $C_{k}$
-tiling covering all but at most
$C_{k}$
-tiling covering all but at most
![]() $\zeta n$
vertices.
$\zeta n$
vertices.
Now we are ready to prove Lemma 2.7 using Lemmas 4.2 and 4.3.
Proof of Lemma
2.7. Given
![]() $k \in 4\mathbb{N}$
and a constant
$k \in 4\mathbb{N}$
and a constant
![]() $\delta$
with
$\delta$
with
![]() $\delta \gt \frac{2}{k}$
, we set
$\delta \gt \frac{2}{k}$
, we set
![]() $\eta \;:\!=\;\delta -\frac{2}{k}$
and choose
$\eta \;:\!=\;\delta -\frac{2}{k}$
and choose
![]() $\frac{1}{n}\ll \alpha \ll \zeta \ll \xi \ll \gamma \ll \eta,\delta$
. Let
$\frac{1}{n}\ll \alpha \ll \zeta \ll \xi \ll \gamma \ll \eta,\delta$
. Let
![]() $G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
$G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_{k}$
with
$C_{k}$
with
![]() $\bar{\delta }(G)\geq (\frac{2}{k}+\eta ) n$
and
$\bar{\delta }(G)\geq (\frac{2}{k}+\eta ) n$
and
![]() $\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
.
$\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
.
By Lemma 4.2 and the choice that
![]() $\gamma \ll \eta,\delta$
, there exists a
$\gamma \ll \eta,\delta$
, there exists a
![]() $\xi$
-absorbing set
$\xi$
-absorbing set
![]() $R\subseteq V(G)$
of size at most
$R\subseteq V(G)$
of size at most
![]() $\gamma n$
for some
$\gamma n$
for some
![]() $\xi \gt 0$
. Let
$\xi \gt 0$
. Let
![]() $G^{\prime }\;:\!=\;G-R$
and note that
$G^{\prime }\;:\!=\;G-R$
and note that
![]() $G^\prime$
is an
$G^\prime$
is an
![]() $(n-\frac{\vert R\vert }{k})$
-blow-up of
$(n-\frac{\vert R\vert }{k})$
-blow-up of
![]() $C_k$
. Then we have
$C_k$
. Then we have
Therefore by applying Lemma 4.3 on
![]() $G^{\prime }$
, we obtain a transversal
$G^{\prime }$
, we obtain a transversal
![]() $C_{k}$
-tiling
$C_{k}$
-tiling
![]() $\mathcal{M}$
that covers all but a set
$\mathcal{M}$
that covers all but a set
![]() $U$
of at most
$U$
of at most
![]() $\zeta n$
vertices in
$\zeta n$
vertices in
![]() $G^{\prime }$
. Since
$G^{\prime }$
. Since
![]() $\zeta \ll \xi$
, the absorbing property of
$\zeta \ll \xi$
, the absorbing property of
![]() $R$
implies that
$R$
implies that
![]() $G[R\cup U]$
contains a transversal
$G[R\cup U]$
contains a transversal
![]() $C_{k}$
-factor, which together with
$C_{k}$
-factor, which together with
![]() $\mathcal{M}$
forms a transversal
$\mathcal{M}$
forms a transversal
![]() $C_{k}$
-factor in
$C_{k}$
-factor in
![]() $G$
.
$G$
.
4.2. Regularity
The proof of Lemma 4.3 is based on a standard application of the regularity method. We will introduce some basic definitions and properties. Given a graph
![]() $G$
and a pair
$G$
and a pair
![]() $(X,Y)$
of vertex-disjoint subsets in
$(X,Y)$
of vertex-disjoint subsets in
![]() $V(G)$
, the density of
$V(G)$
, the density of
![]() $(X,Y)$
is defined as
$(X,Y)$
is defined as
Given constants
![]() $\varepsilon,d\gt 0$
, we say that
$\varepsilon,d\gt 0$
, we say that
![]() $(X,Y)$
is
$(X,Y)$
is
![]() $(\varepsilon,d)$
-regular if
$(\varepsilon,d)$
-regular if
![]() $d(X,Y)\geq d$
and for all
$d(X,Y)\geq d$
and for all
![]() $X^{\prime } \subseteq X$
,
$X^{\prime } \subseteq X$
,
![]() $Y^{\prime } \subseteq Y$
with
$Y^{\prime } \subseteq Y$
with
![]() $\vert X^{\prime } \vert \geq \varepsilon \vert X \vert$
and
$\vert X^{\prime } \vert \geq \varepsilon \vert X \vert$
and
![]() $\vert Y^{\prime } \vert \geq \varepsilon \vert Y \vert$
, we have
$\vert Y^{\prime } \vert \geq \varepsilon \vert Y \vert$
, we have
The following fact results from the definition.
Fact 4.4. Let
![]() $(X,Y)$
be an
$(X,Y)$
be an
![]() $(\varepsilon,d)$
-regular pair and
$(\varepsilon,d)$
-regular pair and
![]() $B \subseteq Y$
with
$B \subseteq Y$
with
![]() $\vert B\vert \ge \varepsilon \vert Y\vert .$
Then all but at most
$\vert B\vert \ge \varepsilon \vert Y\vert .$
Then all but at most
![]() $\varepsilon \vert X\vert$
vertices in
$\varepsilon \vert X\vert$
vertices in
![]() $X$
have at least
$X$
have at least
![]() $(d-\varepsilon )\vert B\vert$
neighbours in
$(d-\varepsilon )\vert B\vert$
neighbours in
![]() $B$
.
$B$
.
We now state a degree form of the regularity lemma (see [Reference Komlós and Simonovits26], Theorem 1.10).
Lemma 4.5. (Degree form of Regularity Lemma [Reference Komlós and Simonovits26]). For every
![]() $\varepsilon \gt 0$
there is an
$\varepsilon \gt 0$
there is an
![]() $N = N(\varepsilon )$
such that the following holds for any real number
$N = N(\varepsilon )$
such that the following holds for any real number
![]() $d\in (0,1]$
and
$d\in (0,1]$
and
![]() $n\in \mathbb{N}$
. Let
$n\in \mathbb{N}$
. Let
![]() $G=(V, E)$
be an
$G=(V, E)$
be an
![]() $n$
-vertex graph. Then there exists a partition
$n$
-vertex graph. Then there exists a partition
![]() $\mathcal{P}=V_{0}\cup V_{1}\cup \dots \cup V_{k}$
and a spanning subgraph
$\mathcal{P}=V_{0}\cup V_{1}\cup \dots \cup V_{k}$
and a spanning subgraph
![]() $G^{\prime } \subseteq G$
with the following properties:
$G^{\prime } \subseteq G$
with the following properties:
-
(a)
 $\frac{1}{\varepsilon } \leq k \leq N$
;
$\frac{1}{\varepsilon } \leq k \leq N$
; -
(b)
 $\vert V_{0} \vert \leq \varepsilon n$
and
$\vert V_{0} \vert \leq \varepsilon n$
and
 $\vert V_{1} \vert =\dots =\vert V_{k} \vert =m\leq \varepsilon n$
;
$\vert V_{1} \vert =\dots =\vert V_{k} \vert =m\leq \varepsilon n$
; -
(c)
 $d_{G^{\prime }}(v)\geq d_{G}(v)-(d+\varepsilon )n$
for all
$d_{G^{\prime }}(v)\geq d_{G}(v)-(d+\varepsilon )n$
for all
 $v \in V(G)$
;
$v \in V(G)$
; -
(d) every
 $V_{i}$
is an independent set in
$V_{i}$
is an independent set in
 $G^{\prime }$
for
$G^{\prime }$
for
 $i\in [k]$
;
$i\in [k]$
; -
(e) every pair
 $(V_{i}, V_{j})$
,
$(V_{i}, V_{j})$
,
 $1 \leq i\lt j \leq k$
is
$1 \leq i\lt j \leq k$
is
 $\varepsilon$
-regular in
$\varepsilon$
-regular in
 $G^{\prime }$
with density
$G^{\prime }$
with density
 $0$
or at least
$0$
or at least
 $d$
.
$d$
.
A widely used auxiliary graph accompanied with the regular partition is the reduced graph. The reduced graph
![]() $R_{d}$
of
$R_{d}$
of
![]() $\mathcal{P}$
is a graph defined on the vertex set
$\mathcal{P}$
is a graph defined on the vertex set
![]() $\left \{ V_{1},\ldots,V_{k} \right \}$
such that
$\left \{ V_{1},\ldots,V_{k} \right \}$
such that
![]() $V_{i}$
is adjacent to
$V_{i}$
is adjacent to
![]() $V_{j}$
in
$V_{j}$
in
![]() $R_{d}$
if
$R_{d}$
if
![]() $(V_{i},V_{j})$
has density at least
$(V_{i},V_{j})$
has density at least
![]() $d$
in
$d$
in
![]() $G^{\prime }$
. We use
$G^{\prime }$
. We use
![]() $d_{R}(V_{i})$
to denote the degree of
$d_{R}(V_{i})$
to denote the degree of
![]() $V_{i}$
in
$V_{i}$
in
![]() $R_{d}$
for each
$R_{d}$
for each
![]() $i\in [k]$
.
$i\in [k]$
.
Fact 4.6. Given positive constants
![]() $d,\varepsilon$
and
$d,\varepsilon$
and
![]() $\delta$
, fix an
$\delta$
, fix an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G=(V,E)$
with
$G=(V,E)$
with
![]() $\delta (G)\geq \delta n$
and let
$\delta (G)\geq \delta n$
and let
![]() $G^{\prime }$
and
$G^{\prime }$
and
![]() $\mathcal{P}$
be obtained by Lemma 4.5, and
$\mathcal{P}$
be obtained by Lemma 4.5, and
![]() $R_{d}$
be given as above. Then for every
$R_{d}$
be given as above. Then for every
![]() $V_{i}\in V(R_{d})$
, we have
$V_{i}\in V(R_{d})$
, we have
![]() $d_{R_d}(V_{i})\geq (\delta -2\varepsilon -d)k$
.
$d_{R_d}(V_{i})\geq (\delta -2\varepsilon -d)k$
.
4.3. Almost perfect tilings
Here we shall make use of the following result which provides a sufficient condition for a transversal path among given sets.
Proposition 4.7.
Given an integer
![]() $k\ge 2$
and a positive constant
$k\ge 2$
and a positive constant
![]() $\alpha \leq \frac{1}{2}$
, let
$\alpha \leq \frac{1}{2}$
, let
![]() $G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
$G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_k$
with
$C_k$
with
![]() $\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
. For any integers
$\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
. For any integers
![]() $i,j$
with
$i,j$
with
![]() $1\leq i\lt j\leq k$
and a collection of subsets
$1\leq i\lt j\leq k$
and a collection of subsets
![]() $X_{s}\subseteq V_s$
with
$X_{s}\subseteq V_s$
with
![]() $s\in [i,j]$
, if
$s\in [i,j]$
, if
![]() $\vert X_{i}\vert$
,
$\vert X_{i}\vert$
,
![]() $\vert X_{j}\vert \geq \alpha n$
and
$\vert X_{j}\vert \geq \alpha n$
and
![]() $\vert X_{\ell }\vert \geq 2\alpha n$
for
$\vert X_{\ell }\vert \geq 2\alpha n$
for
![]() $\ell \in [i+1,j-1]$
(possibly empty), then there exists a transversal path
$\ell \in [i+1,j-1]$
(possibly empty), then there exists a transversal path
![]() $x_{i}x_{i+1}\dots x_{j-1}x_{j}$
where
$x_{i}x_{i+1}\dots x_{j-1}x_{j}$
where
![]() $x_{s}\in X_{s}$
for
$x_{s}\in X_{s}$
for
![]() $s\in [i,j]$
.
$s\in [i,j]$
.
Proof of Proposition
4.7. Without loss of generality, we may take
![]() $i=1$
,
$i=1$
,
![]() $j=k$
for instance. Let
$j=k$
for instance. Let
![]() $Z_{1}\;:\!=\;X_{1}$
and
$Z_{1}\;:\!=\;X_{1}$
and
![]() $Z_{2}\;:\!=\;N(Z_{1})\cap X_{2}$
. By the fact that
$Z_{2}\;:\!=\;N(Z_{1})\cap X_{2}$
. By the fact that
![]() $\alpha ^*_{\textrm{b}}(G)\lt \alpha n\leq \vert Z_{1} \vert, \vert X_{2} \vert$
, it holds that
$\alpha ^*_{\textrm{b}}(G)\lt \alpha n\leq \vert Z_{1} \vert, \vert X_{2} \vert$
, it holds that
![]() $\vert Z_{2}\vert \gt \vert X_{2}\vert -\alpha n\geq \alpha n$
. If
$\vert Z_{2}\vert \gt \vert X_{2}\vert -\alpha n\geq \alpha n$
. If
![]() $k=2$
, then there exists an edge
$k=2$
, then there exists an edge
![]() $\left \{ x_{1},x_{2} \right \}$
between
$\left \{ x_{1},x_{2} \right \}$
between
![]() $Z_1$
and
$Z_1$
and
![]() $Z_2$
and we are done. If
$Z_2$
and we are done. If
![]() $k\gt 2$
, then for each
$k\gt 2$
, then for each
![]() $s\in [k-1]$
, there exist
$s\in [k-1]$
, there exist
![]() $Z_{s}\subseteq X_{s}$
of size larger than
$Z_{s}\subseteq X_{s}$
of size larger than
![]() $\alpha n$
such that
$\alpha n$
such that
![]() $Z_{s}$
is the set of neighbours of
$Z_{s}$
is the set of neighbours of
![]() $Z_{s-1}$
. Since
$Z_{s-1}$
. Since
![]() $\vert Z_{k-1}\vert$
,
$\vert Z_{k-1}\vert$
,
![]() $\vert X_{k} \vert \geq \alpha n$
, there exists an edge
$\vert X_{k} \vert \geq \alpha n$
, there exists an edge
![]() $\left \{ x_{k-1},x_{k} \right \}$
between
$\left \{ x_{k-1},x_{k} \right \}$
between
![]() $Z_{k-1}$
and
$Z_{k-1}$
and
![]() $ X_{k}$
. Therefore, we can find a transversal path
$ X_{k}$
. Therefore, we can find a transversal path
![]() $x_{1}x_{2}\dots x_{k-1}x_{k}$
, where
$x_{1}x_{2}\dots x_{k-1}x_{k}$
, where
![]() $x_{s}\in X_{s}$
for
$x_{s}\in X_{s}$
for
![]() $s\in [k]$
.
$s\in [k]$
.
Now we are ready to prove Lemma 4.3.
Proof of Lemma
4.3. Given
![]() $k\in 4\mathbb{N}$
and
$k\in 4\mathbb{N}$
and
![]() $\delta,\zeta$
with
$\delta,\zeta$
with
![]() $\delta \gt \frac{2}{k}$
, we set
$\delta \gt \frac{2}{k}$
, we set
![]() $\eta \;:\!=\;\delta -\frac{2}{k}$
and choose
$\eta \;:\!=\;\delta -\frac{2}{k}$
and choose
![]() $\frac{1}{n}\ll \alpha \ll \frac{1}{N_{0}}\ll \varepsilon \ll \zeta, \delta,\eta$
. Let
$\frac{1}{n}\ll \alpha \ll \frac{1}{N_{0}}\ll \varepsilon \ll \zeta, \delta,\eta$
. Let
![]() $G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
$G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_{k}$
with
$C_{k}$
with
![]() $\bar{\delta }(G)\geq \delta n$
and
$\bar{\delta }(G)\geq \delta n$
and
![]() $\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
. By applying Lemma 4.5 on
$\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
. By applying Lemma 4.5 on
![]() $G$
with
$G$
with
![]() $d\;:\!=\;\frac{\eta }{4}$
, we obtain a partition
$d\;:\!=\;\frac{\eta }{4}$
, we obtain a partition
![]() $\mathcal{P}=\left \{ U_{0} \right \}\cup \left \{ U_{i,j}\subseteq V_{i}\;:\; i\in [k], j\in [N_{0}] \right \}$
that refines the partition
$\mathcal{P}=\left \{ U_{0} \right \}\cup \left \{ U_{i,j}\subseteq V_{i}\;:\; i\in [k], j\in [N_{0}] \right \}$
that refines the partition
![]() $\{V_1,V_2,\dots,V_k\}$
of
$\{V_1,V_2,\dots,V_k\}$
of
![]() $G$
and a spanning subgraph
$G$
and a spanning subgraph
![]() $G^{\prime }$
of
$G^{\prime }$
of
![]() $G$
with properties
$G$
with properties
![]() $(a)-(e)$
, where we write
$(a)-(e)$
, where we write
![]() $m\;:\!=\;\vert U_{i,j} \vert$
for all
$m\;:\!=\;\vert U_{i,j} \vert$
for all
![]() $i\in [k]$
,
$i\in [k]$
,
![]() $j\in [N_{0}]$
. Let
$j\in [N_{0}]$
. Let
![]() $R_{d}$
be the reduced graph defined on the vertex set
$R_{d}$
be the reduced graph defined on the vertex set
![]() $\left \{ U_{i,j}\;:\; i\in [k], j\in [N_{0}] \right \}$
. For each
$\left \{ U_{i,j}\;:\; i\in [k], j\in [N_{0}] \right \}$
. For each
![]() $i\in [k]$
, let
$i\in [k]$
, let
![]() $\mathcal{V}_{i}=\left \{ U_{i,j}\;:\; j\in [N_{0}] \right \}$
and note that
$\mathcal{V}_{i}=\left \{ U_{i,j}\;:\; j\in [N_{0}] \right \}$
and note that
![]() $\{\mathcal{V}_i\;:\;i\in [k]\}$
is a partition of
$\{\mathcal{V}_i\;:\;i\in [k]\}$
is a partition of
![]() $R_d$
. Then Fact 4.6 implies that
$R_d$
. Then Fact 4.6 implies that
![]() $\bar{\delta }(R_{d})\geq (\delta -\frac{\eta }{2})N_{0}=(\frac{2}{k}+\frac{\eta }{2})N_{0}$
.
$\bar{\delta }(R_{d})\geq (\delta -\frac{\eta }{2})N_{0}=(\frac{2}{k}+\frac{\eta }{2})N_{0}$
.
To obtain an almost perfect transversal
![]() $C_{k}$
-tiling in
$C_{k}$
-tiling in
![]() $G$
, we define an auxiliary graph
$G$
, we define an auxiliary graph
![]() $H$
with
$H$
with
![]() $k$
vertices and two disjoint edges and then use it for embedding copies of transversal
$k$
vertices and two disjoint edges and then use it for embedding copies of transversal
![]() $C_k$
(see Claim 4.9). Now we will show that there exist
$C_k$
(see Claim 4.9). Now we will show that there exist
![]() $N_{0}$
vertex-disjoint copies of specific
$N_{0}$
vertex-disjoint copies of specific
![]() $H$
in
$H$
in
![]() $R_{d}$
.
$R_{d}$
.
Claim 4.8.
For every
![]() $i\in [k-1]$
,
$i\in [k-1]$
,
![]() $R_{d}[\mathcal{V}_{i},\mathcal{V}_{i+1}]$
has a matching of size
$R_{d}[\mathcal{V}_{i},\mathcal{V}_{i+1}]$
has a matching of size
![]() $\min \{N_0, 2\bar \delta (R_{d})\}$
.
$\min \{N_0, 2\bar \delta (R_{d})\}$
.
Proof. Let
![]() $m=\min \{N_0, 2\bar \delta (R_{d})\}$
and without loss of generality, we may take
$m=\min \{N_0, 2\bar \delta (R_{d})\}$
and without loss of generality, we may take
![]() $i=1$
for instance. Let
$i=1$
for instance. Let
![]() $M$
be a maximum matching in
$M$
be a maximum matching in
![]() $R_{d}[\mathcal{V}_{1},\mathcal{V}_{2}]$
and assume for the contrary that
$R_{d}[\mathcal{V}_{1},\mathcal{V}_{2}]$
and assume for the contrary that
![]() $\vert E(M)\vert \leq m-1$
. Let
$\vert E(M)\vert \leq m-1$
. Let
![]() $U$
be the minimum vertex cover of
$U$
be the minimum vertex cover of
![]() $R_{d}[\mathcal{V}_{1},\mathcal{V}_{2}]$
. Then by König’s theorem ([Reference Lovász and Plummer30]), it holds that
$R_{d}[\mathcal{V}_{1},\mathcal{V}_{2}]$
. Then by König’s theorem ([Reference Lovász and Plummer30]), it holds that
![]() $\vert U \vert =\vert E(M) \vert$
. We write
$\vert U \vert =\vert E(M) \vert$
. We write
![]() $A=U\cap \mathcal{V}_{1}$
and
$A=U\cap \mathcal{V}_{1}$
and
![]() $B=U\cap \mathcal{V}_{2}$
. By the pigeonhole principle, we get
$B=U\cap \mathcal{V}_{2}$
. By the pigeonhole principle, we get
![]() $\vert A\vert \leq \lfloor \frac{m-1}{2}\rfloor$
or
$\vert A\vert \leq \lfloor \frac{m-1}{2}\rfloor$
or
![]() $\vert B\vert \leq \lfloor \frac{m-1}{2}\rfloor$
. Suppose
$\vert B\vert \leq \lfloor \frac{m-1}{2}\rfloor$
. Suppose
![]() $\vert A\vert \leq \lfloor \frac{m-1}{2}\rfloor$
. Since
$\vert A\vert \leq \lfloor \frac{m-1}{2}\rfloor$
. Since
![]() $m\leq N_0$
, we have
$m\leq N_0$
, we have
![]() $\vert \mathcal{V}_{2}\backslash B \vert \neq 0$
. Arbitrarily choose
$\vert \mathcal{V}_{2}\backslash B \vert \neq 0$
. Arbitrarily choose
![]() $u\in \mathcal{V}_{2}\backslash B$
, then
$u\in \mathcal{V}_{2}\backslash B$
, then
![]() $u$
has no neighbour in
$u$
has no neighbour in
![]() $\mathcal{V}_{1}\backslash A$
. Thus we have
$\mathcal{V}_{1}\backslash A$
. Thus we have
![]() $d_{\mathcal{V}_{1}}(u)=d_{A}(u)\leq \lfloor \frac{m-1}{2}\rfloor \leq \lfloor \frac{2\bar \delta (R_{d})-1}{2}\rfloor = \bar{\delta }(R_{d})-1$
, a contradiction.
$d_{\mathcal{V}_{1}}(u)=d_{A}(u)\leq \lfloor \frac{m-1}{2}\rfloor \leq \lfloor \frac{2\bar \delta (R_{d})-1}{2}\rfloor = \bar{\delta }(R_{d})-1$
, a contradiction.
By Claim 4.8, for each
![]() $i\in [\frac{k}{2}]$
, there exists a matching
$i\in [\frac{k}{2}]$
, there exists a matching
![]() $M_{i}$
of size
$M_{i}$
of size
![]() $\min \{N_0, 2\bar \delta (R_{d})\}$
between
$\min \{N_0, 2\bar \delta (R_{d})\}$
between
![]() $\mathcal{V}_{2i-1}$
and
$\mathcal{V}_{2i-1}$
and
![]() $\mathcal{V}_{2i}$
. Let
$\mathcal{V}_{2i}$
. Let
![]() $A_{j}\subseteq \mathcal{V}_{j}$
be the vertices uncovered by matchings for
$A_{j}\subseteq \mathcal{V}_{j}$
be the vertices uncovered by matchings for
![]() $j\in [k]$
. We pick a family
$j\in [k]$
. We pick a family
![]() $\mathcal{H}$
of
$\mathcal{H}$
of
![]() $N_{0}$
vertex-disjoint copies of
$N_{0}$
vertex-disjoint copies of
![]() $H$
such that each copy contains two disjoint edges
$H$
such that each copy contains two disjoint edges
![]() $e_{1}$
and
$e_{1}$
and
![]() $e_{2}$
where
$e_{2}$
where
![]() $e_{1}\in M_{2i-1}$
and
$e_{1}\in M_{2i-1}$
and
![]() $e_{2}\in M_{2i}$
for some
$e_{2}\in M_{2i}$
for some
![]() $i\in [\frac{k}{4}]$
and exactly one vertex inside each
$i\in [\frac{k}{4}]$
and exactly one vertex inside each
![]() $A_{j}$
for
$A_{j}$
for
![]() $j\in [k]\backslash \left \{4i-3,4i-2, 4i-1,4i\right \}$
. Since
$j\in [k]\backslash \left \{4i-3,4i-2, 4i-1,4i\right \}$
. Since
 \begin{equation*} \sum _{i=1}^{\frac{k}{4}}\vert M_{2i-1} \vert = \frac{k}{4}\cdot \min \{N_0, 2\bar \delta (R_{d})\} \geq N_{0}, \end{equation*}
\begin{equation*} \sum _{i=1}^{\frac{k}{4}}\vert M_{2i-1} \vert = \frac{k}{4}\cdot \min \{N_0, 2\bar \delta (R_{d})\} \geq N_{0}, \end{equation*}
and similarly
![]() $\sum _{i=1}^{k/4} \vert M_{2i}\vert \ge N_0$
, we can greedily find
$\sum _{i=1}^{k/4} \vert M_{2i}\vert \ge N_0$
, we can greedily find
![]() $N_{0}$
vertex-disjoint copies of
$N_{0}$
vertex-disjoint copies of
![]() $H$
that together cover all vertices in
$H$
that together cover all vertices in
![]() $R_{d}$
.
$R_{d}$
.
Claim 4.9.
For each copy of
![]() $H$
in
$H$
in
![]() $\mathcal{H}$
, we can find a transversal
$\mathcal{H}$
, we can find a transversal
![]() $C_{k}$
-tiling covering all but at most
$C_{k}$
-tiling covering all but at most
![]() $\frac{\zeta m}{2}$
vertices in the union of its clusters in
$\frac{\zeta m}{2}$
vertices in the union of its clusters in
![]() $G$
.
$G$
.
Proof of Claim
4.9. Given a copy of
![]() $H$
, without loss of generality, we may assume that
$H$
, without loss of generality, we may assume that
![]() $V(H)=\left \{U_{1,1}, U_{2,2},\ldots,U_{k,k}\right \}$
and
$V(H)=\left \{U_{1,1}, U_{2,2},\ldots,U_{k,k}\right \}$
and
![]() $\left \{U_{1,1}, U_{2,2}\right \}$
,
$\left \{U_{1,1}, U_{2,2}\right \}$
,
![]() $\left \{U_{3,3}, U_{4,4}\right \} \in E(H)$
. Therefore
$\left \{U_{3,3}, U_{4,4}\right \} \in E(H)$
. Therefore
![]() $(U_{1,1},U_{2,2})$
and
$(U_{1,1},U_{2,2})$
and
![]() $(U_{3,3},U_{4,4})$
are
$(U_{3,3},U_{4,4})$
are
![]() $(\varepsilon,d)$
-regular in
$(\varepsilon,d)$
-regular in
![]() $G^\prime$
. Now it suffices to show that for any
$G^\prime$
. Now it suffices to show that for any
![]() $Z_{i}\subseteq U_{i,i}$
with
$Z_{i}\subseteq U_{i,i}$
with
![]() $i\in [k]$
each of size at least
$i\in [k]$
each of size at least
![]() $\frac{\zeta m}{2k}$
, there exists a copy of
$\frac{\zeta m}{2k}$
, there exists a copy of
![]() $C_{k}$
with exactly one vertex inside each
$C_{k}$
with exactly one vertex inside each
![]() $Z_{i}$
.
$Z_{i}$
.
Since
![]() $\vert Z_{i} \vert \geq \frac{\zeta m}{2k} \ge \varepsilon m$
for
$\vert Z_{i} \vert \geq \frac{\zeta m}{2k} \ge \varepsilon m$
for
![]() $i\in [4]$
, Fact 4.4 implies that there exists a subset
$i\in [4]$
, Fact 4.4 implies that there exists a subset
![]() $Z_{2}^{\prime }\subseteq Z_{2}$
of size at least
$Z_{2}^{\prime }\subseteq Z_{2}$
of size at least
![]() $\vert Z_{2} \vert -\varepsilon m$
such that every vertex in
$\vert Z_{2} \vert -\varepsilon m$
such that every vertex in
![]() $Z_{2}^{\prime }$
has at least
$Z_{2}^{\prime }$
has at least
![]() $(d-\varepsilon )\vert Z_{1} \vert$
neighbours inside
$(d-\varepsilon )\vert Z_{1} \vert$
neighbours inside
![]() $Z_{1}$
and a subset
$Z_{1}$
and a subset
![]() $Z_{3}^{\prime }\subseteq Z_{3}$
of size at least
$Z_{3}^{\prime }\subseteq Z_{3}$
of size at least
![]() $\vert Z_{3} \vert -\varepsilon m$
such that every vertex in
$\vert Z_{3} \vert -\varepsilon m$
such that every vertex in
![]() $Z_{3}^{\prime }$
has at least
$Z_{3}^{\prime }$
has at least
![]() $(d-\varepsilon )\vert Z_{4} \vert$
neighbours inside
$(d-\varepsilon )\vert Z_{4} \vert$
neighbours inside
![]() $Z_{4}$
respectively.
$Z_{4}$
respectively.
By the assumption
![]() $\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
and the fact that
$\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
and the fact that
![]() $\vert Z_2^\prime \vert, \vert Z_3^\prime \vert \ge \frac{\zeta m}{2k}-\varepsilon m \ge \alpha n$
, there is at least one edge between
$\vert Z_2^\prime \vert, \vert Z_3^\prime \vert \ge \frac{\zeta m}{2k}-\varepsilon m \ge \alpha n$
, there is at least one edge between
![]() $Z_{2}^{\prime }$
and
$Z_{2}^{\prime }$
and
![]() $Z_{3}^{\prime }$
. Arbitrarily choose one edge
$Z_{3}^{\prime }$
. Arbitrarily choose one edge
![]() $\left \{u,v\right \}$
with
$\left \{u,v\right \}$
with
![]() $u\in Z_2'$
and
$u\in Z_2'$
and
![]() $v\in Z_3'$
, and let
$v\in Z_3'$
, and let
![]() $Q_{1}=N(u)\cap Z_{1}$
and
$Q_{1}=N(u)\cap Z_{1}$
and
![]() $Q_{2}=N(v)\cap Z_{4}$
, respectively. Then we have
$Q_{2}=N(v)\cap Z_{4}$
, respectively. Then we have
![]() $\vert Q_{1} \vert,\vert Q_{2} \vert \geq (d-\varepsilon )\cdot \frac{\zeta m}{2k}\geq \alpha n$
and note that
$\vert Q_{1} \vert,\vert Q_{2} \vert \geq (d-\varepsilon )\cdot \frac{\zeta m}{2k}\geq \alpha n$
and note that
![]() $\vert Z_i\vert \ge \frac{\zeta m}{2k}\ge 2\alpha n$
for every
$\vert Z_i\vert \ge \frac{\zeta m}{2k}\ge 2\alpha n$
for every
![]() $i\in [k]$
. By applying Proposition 4.7 with
$i\in [k]$
. By applying Proposition 4.7 with
![]() $X_{i}\;:\!=\;Q_{1}$
and
$X_{i}\;:\!=\;Q_{1}$
and
![]() $X_{j}\;:\!=\;Q_{2}$
, we can obtain a transversal path of length
$X_{j}\;:\!=\;Q_{2}$
, we can obtain a transversal path of length
![]() $k-3$
, where the ends in
$k-3$
, where the ends in
![]() $Q_{1}$
and
$Q_{1}$
and
![]() $Q_{2}$
are denoted by
$Q_{2}$
are denoted by
![]() $u^{\prime }$
and
$u^{\prime }$
and
![]() $v^{\prime }$
, respectively. Together with three edges
$v^{\prime }$
, respectively. Together with three edges
![]() $\left \{u^{\prime },u\right \}$
,
$\left \{u^{\prime },u\right \}$
,
![]() $\left \{u,v\right \}$
,
$\left \{u,v\right \}$
,
![]() $\left \{v,v^{\prime }\right \}$
, we can construct a copy of transversal
$\left \{v,v^{\prime }\right \}$
, we can construct a copy of transversal
![]() $C_{k}$
in
$C_{k}$
in
![]() $\cup _{i=1}^{k}Z_{i}$
. Thus we can obtain a transversal
$\cup _{i=1}^{k}Z_{i}$
. Thus we can obtain a transversal
![]() $C_{k}$
-tiling covering all but at most
$C_{k}$
-tiling covering all but at most
![]() $\frac{\zeta m}{2}$
vertices in
$\frac{\zeta m}{2}$
vertices in
![]() $\cup _{i=1}^{k} U_{i,i}$
in
$\cup _{i=1}^{k} U_{i,i}$
in
![]() $G$
.
$G$
.
This would finish the proof as the union of these
![]() $C_{k}$
-tilings taken over all copies of
$C_{k}$
-tilings taken over all copies of
![]() $H$
in
$H$
in
![]() $\mathcal{H}$
would leave at most
$\mathcal{H}$
would leave at most
vertices uncovered.
4.4. Building an absorbing set
A typical step in the absorption method for
![]() $F$
-factor is to show that every
$F$
-factor is to show that every
![]() $k\;:\!=\;\vert V(F) \vert$
-set has polynomially many absorbers (see [Reference Han, Hu, Wang and Yang14]). However, it remains unclear whether this property holds in our setting. Instead, a new approach due to Nenadov and Pehova [Reference Nenadov and Pehova35] guarantees an absorbing set provided that every
$k\;:\!=\;\vert V(F) \vert$
-set has polynomially many absorbers (see [Reference Han, Hu, Wang and Yang14]). However, it remains unclear whether this property holds in our setting. Instead, a new approach due to Nenadov and Pehova [Reference Nenadov and Pehova35] guarantees an absorbing set provided that every
![]() $k$
-set has linearly many vertex-disjoint absorbers. Since the host graph in Lemma 4.2 is
$k$
-set has linearly many vertex-disjoint absorbers. Since the host graph in Lemma 4.2 is
![]() $k$
-partite, we aim to show that every transversal
$k$
-partite, we aim to show that every transversal
![]() $k$
-set has linearly many vertex-disjoint absorbers. For this, we shall make use of the lattice-based absorbing method developed by Han [Reference Han13].
$k$
-set has linearly many vertex-disjoint absorbers. For this, we shall make use of the lattice-based absorbing method developed by Han [Reference Han13].
4.4.1. Finding absorbers
To illustrate the lattice-based absorbing method, we introduce some definitions. Let
![]() $G, F$
be given as aforementioned and
$G, F$
be given as aforementioned and
![]() $m, t$
be positive integers. Then we say that two vertices
$m, t$
be positive integers. Then we say that two vertices
![]() $u,v\in V(G)$
are
$u,v\in V(G)$
are
![]() $(F, m, t)$
-reachable (in
$(F, m, t)$
-reachable (in
![]() $G$
) if for any set
$G$
) if for any set
![]() $W$
of
$W$
of
![]() $m$
vertices, there is a set
$m$
vertices, there is a set
![]() $S\subseteq V(G)\backslash W$
of size at most
$S\subseteq V(G)\backslash W$
of size at most
![]() $kt-1$
such that both
$kt-1$
such that both
![]() $G[\!\left \{u \right \}\cup S]$
and
$G[\!\left \{u \right \}\cup S]$
and
![]() $G[\!\left \{v \right \}\cup S]$
have
$G[\!\left \{v \right \}\cup S]$
have
![]() $F$
-factors, where we call such
$F$
-factors, where we call such
![]() $S$
an
$S$
an
![]() $F$
-
$F$
-
![]() $\textit{connector}$
for
$\textit{connector}$
for
![]() $u, v$
. Moreover, a set
$u, v$
. Moreover, a set
![]() $U\subseteq V(G)$
is
$U\subseteq V(G)$
is
![]() $(F, m, t)$
-
$(F, m, t)$
-
![]() $\textit{closed}$
if every two vertices
$\textit{closed}$
if every two vertices
![]() $u, v$
in
$u, v$
in
![]() $U$
are
$U$
are
![]() $(F, m, t)$
-reachable, where the corresponding
$(F, m, t)$
-reachable, where the corresponding
![]() $F$
-connector for
$F$
-connector for
![]() $u, v$
may not be included in
$u, v$
may not be included in
![]() $U$
.
$U$
.
The following result builds a sufficient condition to ensure that every transversal
![]() $k$
-set has linearly many vertex-disjoint absorbers.
$k$
-set has linearly many vertex-disjoint absorbers.
Lemma 4.10.
Given
![]() $k \in \mathbb{N}$
with
$k \in \mathbb{N}$
with
![]() $k\geq 4$
and a constant
$k\geq 4$
and a constant
![]() $\delta \gt \frac{2}{k}$
, there exist
$\delta \gt \frac{2}{k}$
, there exist
![]() $\alpha,\beta \gt 0$
such that the following holds for sufficiently large
$\alpha,\beta \gt 0$
such that the following holds for sufficiently large
![]() $n \in \mathbb{N}$
. Let
$n \in \mathbb{N}$
. Let
![]() $G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the n-blow-up of
$G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the n-blow-up of
![]() $C_{k}$
with
$C_{k}$
with
![]() $\bar{\delta }(G)\geq \delta n$
and
$\bar{\delta }(G)\geq \delta n$
and
![]() $\alpha ^*_{\mathrm{b}}(G)\lt \alpha n$
. Then every transversal
$\alpha ^*_{\mathrm{b}}(G)\lt \alpha n$
. Then every transversal
![]() $k$
-set in
$k$
-set in
![]() $G$
has at least
$G$
has at least
![]() $ \frac{\beta n-k}{4k^2}$
vertex-disjoint
$ \frac{\beta n-k}{4k^2}$
vertex-disjoint
![]() $(C_{k},2k)$
-absorbers.
$(C_{k},2k)$
-absorbers.
4.4.2. Proof of Lemma 4.2
In order to prove the existence of an absorbing set, we introduce a notion of
![]() $F$
-fan.
$F$
-fan.
Definition 4.11. ([Reference Han, Morris, Wang and Yang15]) For a vertex
![]() $v\in V(G)$
and a
$v\in V(G)$
and a
![]() $k$
-vertex graph
$k$
-vertex graph
![]() $F$
, an
$F$
, an
![]() $F$
-fan
$F$
-fan
![]() $\mathcal{F}_{v}$
at
$\mathcal{F}_{v}$
at
![]() $v$
in
$v$
in
![]() $V(G)$
is a collection of pairwise disjoint sets
$V(G)$
is a collection of pairwise disjoint sets
![]() $S\subseteq V(G)\backslash \left \{v \right \}$
such that for each
$S\subseteq V(G)\backslash \left \{v \right \}$
such that for each
![]() $S\in \mathcal{F}_{v}$
we have that
$S\in \mathcal{F}_{v}$
we have that
![]() $\vert S\vert =k-1$
and
$\vert S\vert =k-1$
and
![]() $\left \{v \right \}\cup S$
spans a copy of
$\left \{v \right \}\cup S$
spans a copy of
![]() $F$
.
$F$
.
To build an absorbing structure, we shall make use of bipartite templates as follows, which was introduced by Montgomery [Reference Montgomery34].
Lemma 4.12.
Let
![]() $\beta \gt 0$
. There exists
$\beta \gt 0$
. There exists
![]() $m_{0}$
such that the following holds for every
$m_{0}$
such that the following holds for every
![]() $m\geq m_{0}$
. There exists a bipartite graph
$m\geq m_{0}$
. There exists a bipartite graph
![]() $B_{m}$
with vertex classes
$B_{m}$
with vertex classes
![]() $X_{m}\cup Y_{m}$
and
$X_{m}\cup Y_{m}$
and
![]() $Z_{m}$
and maximum degree 40, such that
$Z_{m}$
and maximum degree 40, such that
![]() $\vert X_{m}\vert =m+\beta m$
,
$\vert X_{m}\vert =m+\beta m$
,
![]() $\vert Y_{m}\vert =2m$
and
$\vert Y_{m}\vert =2m$
and
![]() $\vert Z_{m}\vert =3m$
, and for every subset
$\vert Z_{m}\vert =3m$
, and for every subset
![]() $X^{\prime }_{m}\subseteq X_{m}$
of size
$X^{\prime }_{m}\subseteq X_{m}$
of size
![]() $\vert X^{\prime }_{m}\vert =m$
, the induced graph
$\vert X^{\prime }_{m}\vert =m$
, the induced graph
![]() $B[X^{\prime }_{m}\cup Y_{m},Z_{m}]$
contains a perfect matching.
$B[X^{\prime }_{m}\cup Y_{m},Z_{m}]$
contains a perfect matching.
Proof of Lemma
4.2. Given
![]() $k \in \mathbb{N}$
with
$k \in \mathbb{N}$
with
![]() $k\geq 4$
and positive constants
$k\geq 4$
and positive constants
![]() $\delta \gt \frac{2}{k}$
and
$\delta \gt \frac{2}{k}$
and
![]() $\gamma \leq \frac{\delta }{2}$
, we choose
$\gamma \leq \frac{\delta }{2}$
, we choose
![]() $\frac{1}{n}\ll \alpha \ll \xi \ll \beta \ll \delta,\gamma, \frac{1}{k}$
. Let
$\frac{1}{n}\ll \alpha \ll \xi \ll \beta \ll \delta,\gamma, \frac{1}{k}$
. Let
![]() $G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
$G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_{k}$
with
$C_{k}$
with
![]() $\bar{\delta }(G)\geq \delta n$
and
$\bar{\delta }(G)\geq \delta n$
and
![]() $\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
. Lemma 4.10 implies that every transversal
$\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
. Lemma 4.10 implies that every transversal
![]() $k$
-set in
$k$
-set in
![]() $G$
has at least
$G$
has at least
![]() $\frac{\beta n-k}{4k^2}$
vertex-disjoint
$\frac{\beta n-k}{4k^2}$
vertex-disjoint
![]() $(C_{k},2k)$
-absorbers. Let
$(C_{k},2k)$
-absorbers. Let
![]() $\tau \;:\!=\;\frac{\beta }{8k^2}$
. Then for every
$\tau \;:\!=\;\frac{\beta }{8k^2}$
. Then for every
![]() $v\in V(G)$
, there is a
$v\in V(G)$
, there is a
![]() $C_k$
-fan
$C_k$
-fan
![]() $\mathcal{F}_{v}$
in
$\mathcal{F}_{v}$
in
![]() $V(G)$
of size at least
$V(G)$
of size at least
![]() $ \frac{\beta n-k}{4k^2}\ge \tau n$
. Now it suffices to find a
$ \frac{\beta n-k}{4k^2}\ge \tau n$
. Now it suffices to find a
![]() $\xi$
-absorbing set
$\xi$
-absorbing set
![]() $R$
for some
$R$
for some
![]() $\xi \gt 0$
such that
$\xi \gt 0$
such that
![]() $\vert R \vert \leq \tau n\leq \gamma n$
.
$\vert R \vert \leq \tau n\leq \gamma n$
.
Let
![]() $q=\frac{\tau }{1000k^3}$
and
$q=\frac{\tau }{1000k^3}$
and
![]() $\beta ^{\prime }=\frac{q^{k-1}\tau }{2k}$
. For
$\beta ^{\prime }=\frac{q^{k-1}\tau }{2k}$
. For
![]() $i\in [k]$
, let
$i\in [k]$
, let
![]() $X_{i}\subseteq V_{i}$
be a set of size
$X_{i}\subseteq V_{i}$
be a set of size
![]() $qn$
chosen uniformly at random. For every
$qn$
chosen uniformly at random. For every
![]() $v\in V(G)$
, let
$v\in V(G)$
, let
![]() $f_{v}$
denote the number of the sets from
$f_{v}$
denote the number of the sets from
![]() $\mathcal{F}_{v}$
that lie inside
$\mathcal{F}_{v}$
that lie inside
![]() $\cup _{i=1}^{k} X_{i}$
. Note that
$\cup _{i=1}^{k} X_{i}$
. Note that
![]() $\mu \;:\!=\;\mathbb{E}[f_{v}]= q^{k-1}\vert \mathcal{F}_{v} \vert \geq q^{k-1}\tau n$
. By the union bound and Chernoff’s inequality, we have
$\mu \;:\!=\;\mathbb{E}[f_{v}]= q^{k-1}\vert \mathcal{F}_{v} \vert \geq q^{k-1}\tau n$
. By the union bound and Chernoff’s inequality, we have
 \begin{equation*} \mathbb{P}\left [\,\textrm{there}\ \textrm{is}\ v\in V(G)\ \textrm{with}\ f_{v}\lt \frac{\mu }{2}\,\right ]\leq kn\, \textrm{exp}\left (\frac{-(\mu/2)^2}{2\mu }\right )\leq kn\, \textrm{exp}\left (-\frac{q^{k-1}\tau }{8}n\right )=o(1). \end{equation*}
\begin{equation*} \mathbb{P}\left [\,\textrm{there}\ \textrm{is}\ v\in V(G)\ \textrm{with}\ f_{v}\lt \frac{\mu }{2}\,\right ]\leq kn\, \textrm{exp}\left (\frac{-(\mu/2)^2}{2\mu }\right )\leq kn\, \textrm{exp}\left (-\frac{q^{k-1}\tau }{8}n\right )=o(1). \end{equation*}
Therefore, as
![]() $n$
is sufficiently large, there exist
$n$
is sufficiently large, there exist
![]() $X_{i}\subseteq V_{i}$
with
$X_{i}\subseteq V_{i}$
with
![]() $\vert X_{i} \vert = qn$
such that for each
$\vert X_{i} \vert = qn$
such that for each
![]() $v\in V(G)$
, there is a subfamily
$v\in V(G)$
, there is a subfamily
![]() $\mathcal{F}_{v}^{\prime }$
of at least
$\mathcal{F}_{v}^{\prime }$
of at least
![]() $\frac{q^{k-1}\tau n}{2}= k\beta ^{\prime }n$
sets from
$\frac{q^{k-1}\tau n}{2}= k\beta ^{\prime }n$
sets from
![]() $\mathcal{F}_{v}$
contained in
$\mathcal{F}_{v}$
contained in
![]() $\cup _{i=1}^{k} X_{i}$
.
$\cup _{i=1}^{k} X_{i}$
.
Let
![]() $m=\vert X_{i} \vert/(1+\beta ^{\prime })$
and note that
$m=\vert X_{i} \vert/(1+\beta ^{\prime })$
and note that
![]() $m$
is linear in
$m$
is linear in
![]() $n$
. Let
$n$
. Let
![]() $\left \{ I_{i} \right \}_{i\in [k]}$
be a partition of
$\left \{ I_{i} \right \}_{i\in [k]}$
be a partition of
![]() [$3\textit{km}$]
with each
[$3\textit{km}$]
with each
![]() $\vert I_{i} \vert =3{m}$
. For
$\vert I_{i} \vert =3{m}$
. For
![]() $i\in [k]$
, arbitrarily choose
$i\in [k]$
, arbitrarily choose
![]() $k$
vertex-disjoint subsets
$k$
vertex-disjoint subsets
![]() $Y_{i}$
,
$Y_{i}$
,
![]() $ Z_{i,j}$
for
$ Z_{i,j}$
for
![]() $j\in [k]\backslash \left \{ i\right \}$
in
$j\in [k]\backslash \left \{ i\right \}$
in
![]() $V_{i}\backslash X_{i}$
with
$V_{i}\backslash X_{i}$
with
![]() $\vert Y_{i}\vert =2{m}$
and
$\vert Y_{i}\vert =2{m}$
and
![]() $\vert Z_{i,j}\vert =3{m}$
. Let
$\vert Z_{i,j}\vert =3{m}$
. Let
![]() $X=\cup _{i=1}^{k} X_{i}$
,
$X=\cup _{i=1}^{k} X_{i}$
,
![]() $Y=\cup _{i=1}^{k} Y_{i}$
and
$Y=\cup _{i=1}^{k} Y_{i}$
and
![]() $ Z=\cup Z_{i,j}$
. Then we have
$ Z=\cup Z_{i,j}$
. Then we have
![]() $\vert X\vert =(1+\beta ^{\prime }){km}$
,
$\vert X\vert =(1+\beta ^{\prime }){km}$
,
![]() $\vert Y\vert = 2{km}$
and
$\vert Y\vert = 2{km}$
and
![]() $\vert Z \vert =3k(k-1)m$
. For each
$\vert Z \vert =3k(k-1)m$
. For each
![]() $j\in [k]$
, we partition
$j\in [k]$
, we partition
![]() $\cup _{i\in [k]\backslash \left \{ j \right \}}Z_{i,j}$
into a family
$\cup _{i\in [k]\backslash \left \{ j \right \}}Z_{i,j}$
into a family
![]() $\mathcal{Z}_j$
of
$\mathcal{Z}_j$
of
![]() $3m$
transversal
$3m$
transversal
![]() $(k-1)$
-sets and take an arbitrary bijection
$(k-1)$
-sets and take an arbitrary bijection
![]() $\phi _{j}\;:\;\mathcal{Z}_j\rightarrow I_{j}$
. Moreover, we define a function
$\phi _{j}\;:\;\mathcal{Z}_j\rightarrow I_{j}$
. Moreover, we define a function
![]() $\varphi$
on
$\varphi$
on
![]() $[3km]$
such that
$[3km]$
such that
![]() $\varphi (x)\;:\!=\;\phi ^{-1}_{j}(x)$
if
$\varphi (x)\;:\!=\;\phi ^{-1}_{j}(x)$
if
![]() $x\in I_{j}$
. Let
$x\in I_{j}$
. Let
![]() $ T_{i}$
be the bipartite graph obtained by Lemma 4.12 with vertex classes
$ T_{i}$
be the bipartite graph obtained by Lemma 4.12 with vertex classes
![]() $X_{i}\cup Y_{i}$
and
$X_{i}\cup Y_{i}$
and
![]() $I_{i}$
, and let
$I_{i}$
, and let
![]() $T=\cup _{i=1}^{k} T_{i}$
. Then
$T=\cup _{i=1}^{k} T_{i}$
. Then
![]() $T$
is a bipartite graph between
$T$
is a bipartite graph between
![]() $X\cup Y$
and
$X\cup Y$
and
![]() $[3km]$
with
$[3km]$
with
![]() $\Delta (T)\leq 40$
.
$\Delta (T)\leq 40$
.
We claim that there exists a family
![]() $\left \{ A_{e} \right \}_{e\in E(T)}$
of pairwise vertex-disjoint subsets in
$\left \{ A_{e} \right \}_{e\in E(T)}$
of pairwise vertex-disjoint subsets in
![]() $V(G)\backslash (X\cup Y\cup Z)$
such that for every
$V(G)\backslash (X\cup Y\cup Z)$
such that for every
![]() $e=\left \{ w_{1},w_{2} \right \}\in E(T)$
with
$e=\left \{ w_{1},w_{2} \right \}\in E(T)$
with
![]() $w_{1}\in X\cup Y$
and
$w_{1}\in X\cup Y$
and
![]() $w_{2}\in [3km]$
, the set
$w_{2}\in [3km]$
, the set
![]() $A_{e}$
is a
$A_{e}$
is a
![]() $(C_{k}, 2k)$
-absorber for the transversal
$(C_{k}, 2k)$
-absorber for the transversal
![]() $k$
-set
$k$
-set
![]() $\left \{ w_{1} \right \}\cup \varphi (w_{2})$
. Indeed otherwise, there exists an edge
$\left \{ w_{1} \right \}\cup \varphi (w_{2})$
. Indeed otherwise, there exists an edge
![]() $e^{\prime }\in E(T)$
without such a subset. Recall that
$e^{\prime }\in E(T)$
without such a subset. Recall that
![]() $m=\frac{qn}{1+\beta ^{\prime }}$
and
$m=\frac{qn}{1+\beta ^{\prime }}$
and
![]() $\Delta (T)\leq 40$
, then we have
$\Delta (T)\leq 40$
, then we have
 \begin{equation*} \vert X\vert +\vert Y\vert +\vert Z\vert +\left \vert \bigcup _{e\in E(T)\backslash \left \{ e^{\prime }\right \}} A_{e} \right \vert \leq 4km+3km(k-1)+2k^2\vert E(T) \vert \leq 4k^2m+80k^2\cdot 3km\leq \frac{\tau n}{2}. \end{equation*}
\begin{equation*} \vert X\vert +\vert Y\vert +\vert Z\vert +\left \vert \bigcup _{e\in E(T)\backslash \left \{ e^{\prime }\right \}} A_{e} \right \vert \leq 4km+3km(k-1)+2k^2\vert E(T) \vert \leq 4k^2m+80k^2\cdot 3km\leq \frac{\tau n}{2}. \end{equation*}
Since every transversal
![]() $k$
-set has at least
$k$
-set has at least
![]() $\tau n$
vertex-disjoint
$\tau n$
vertex-disjoint
![]() $(C_{k}, 2k)$
-absorbers in
$(C_{k}, 2k)$
-absorbers in
![]() $G$
, we can choose one in
$G$
, we can choose one in
![]() $V(G)\backslash (X \cup Y \cup Z\cup \bigcup _{e\in E(T)\backslash \left \{ e^{\prime }\right \}}A_{e})$
as the subset
$V(G)\backslash (X \cup Y \cup Z\cup \bigcup _{e\in E(T)\backslash \left \{ e^{\prime }\right \}}A_{e})$
as the subset
![]() $A_{e^{\prime }}$
, a contradiction.
$A_{e^{\prime }}$
, a contradiction.
Let
![]() $R=X \cup Y \cup Z\cup \bigcup _{e\in E(T)}A_{e}$
. Then
$R=X \cup Y \cup Z\cup \bigcup _{e\in E(T)}A_{e}$
. Then
![]() $\vert R \vert \leq \tau n$
and we claim that
$\vert R \vert \leq \tau n$
and we claim that
![]() $R$
is a
$R$
is a
![]() $\xi$
-absorbing set in
$\xi$
-absorbing set in
![]() $G$
. Indeed, for an arbitrary balanced subset
$G$
. Indeed, for an arbitrary balanced subset
![]() $U\subseteq V(G)\backslash R$
with
$U\subseteq V(G)\backslash R$
with
![]() $\vert U\vert \leq \xi n$
, we shall verify that
$\vert U\vert \leq \xi n$
, we shall verify that
![]() $G[R\cup U]$
admits a
$G[R\cup U]$
admits a
![]() $C_k$
-factor. Note that if there exist
$C_k$
-factor. Note that if there exist
![]() $Q_{i}\subseteq X_{i}$
with
$Q_{i}\subseteq X_{i}$
with
![]() $\vert Q_{i} \vert =\beta ^{\prime }m$
for
$\vert Q_{i} \vert =\beta ^{\prime }m$
for
![]() $i\in [k]$
and a transversal
$i\in [k]$
and a transversal
![]() $C_{k}$
-factor in
$C_{k}$
-factor in
![]() $G[\bigcup _{i=1}^{k} Q_{i}\cup U]$
, then
$G[\bigcup _{i=1}^{k} Q_{i}\cup U]$
, then
![]() $G[R\cup U]$
contains a transversal
$G[R\cup U]$
contains a transversal
![]() $C_{k}$
-factor. In fact by setting
$C_{k}$
-factor. In fact by setting
![]() $X_{i}^{\prime }=X_{i}\backslash Q_{i}$
, Lemma 4.12 implies that there is a perfect matching
$X_{i}^{\prime }=X_{i}\backslash Q_{i}$
, Lemma 4.12 implies that there is a perfect matching
![]() $M$
in
$M$
in
![]() $T$
between
$T$
between
![]() $ \bigcup _{i=1}^{k} X_{i}^{\prime }\cup Y$
and
$ \bigcup _{i=1}^{k} X_{i}^{\prime }\cup Y$
and
![]() $[3km]$
. For each edge
$[3km]$
. For each edge
![]() $e=\left \{ w_{1},w_{2} \right \}\in M$
take a transversal
$e=\left \{ w_{1},w_{2} \right \}\in M$
take a transversal
![]() $C_{k}$
-factor in
$C_{k}$
-factor in
![]() $G[\!\left \{ w_{1} \right \}\cup \varphi (w_{2})\cup A_{e}]$
and for each
$G[\!\left \{ w_{1} \right \}\cup \varphi (w_{2})\cup A_{e}]$
and for each
![]() $e^\prime \in E(T)\backslash M$
take a transversal
$e^\prime \in E(T)\backslash M$
take a transversal
![]() $C_{k}$
-factor in
$C_{k}$
-factor in
![]() $G[A_{e^\prime }]$
, which forms a transversal
$G[A_{e^\prime }]$
, which forms a transversal
![]() $C_{k}$
-factor of
$C_{k}$
-factor of
![]() $G[R\backslash \cup _{i=1}^{k} Q_{i}]$
. Thus together with the above assumption, we can obtain a transversal
$G[R\backslash \cup _{i=1}^{k} Q_{i}]$
. Thus together with the above assumption, we can obtain a transversal
![]() $C_{k}$
-factor in
$C_{k}$
-factor in
![]() $G[R\cup U]$
.
$G[R\cup U]$
.
Hence, it suffices to find the desired
![]() $Q_{i}$
as above. Recall that every
$Q_{i}$
as above. Recall that every
![]() $v\in V(G)$
has a subfamily
$v\in V(G)$
has a subfamily
![]() $\mathcal{F}_{v}^{\prime }$
of at least
$\mathcal{F}_{v}^{\prime }$
of at least
![]() $k\beta ^{\prime }n$
sets in
$k\beta ^{\prime }n$
sets in
![]() $\cup _{i=1}^{k} X_{i}$
. By the choice that
$\cup _{i=1}^{k} X_{i}$
. By the choice that
![]() $\xi \ll \beta,\frac{1}{k}$
and thus
$\xi \ll \beta,\frac{1}{k}$
and thus
![]() $\vert U\vert \leq \xi n\leq \beta ^{\prime }n$
, one can greedily find a family
$\vert U\vert \leq \xi n\leq \beta ^{\prime }n$
, one can greedily find a family
![]() $\mathcal{C}_{1}$
of vertex-disjoint copies of transversal
$\mathcal{C}_{1}$
of vertex-disjoint copies of transversal
![]() $C_{k}$
covering
$C_{k}$
covering
![]() $U$
with vertices in
$U$
with vertices in
![]() $\cup _{i=1}^{k}X_{i}$
. Let
$\cup _{i=1}^{k}X_{i}$
. Let
![]() $Q_{i1}\;:\!=\;X_{i}\cap V(\mathcal{C}_{1})$
. Then we have
$Q_{i1}\;:\!=\;X_{i}\cap V(\mathcal{C}_{1})$
. Then we have
![]() $\vert Q_{i1}\vert =\frac{k-1}{k}\vert U \vert$
and
$\vert Q_{i1}\vert =\frac{k-1}{k}\vert U \vert$
and
![]() $\mathcal{C}_1$
is a transversal
$\mathcal{C}_1$
is a transversal
![]() $C_{k}$
-factor in
$C_{k}$
-factor in
![]() $G[\bigcup _{i=1}^{k} Q_{i1}\cup U]$
. Moreover, one can greedily pick a family
$G[\bigcup _{i=1}^{k} Q_{i1}\cup U]$
. Moreover, one can greedily pick a family
![]() $\mathcal{C}_{2}$
of
$\mathcal{C}_{2}$
of
![]() $\beta ^{\prime }m-\frac{k-1}{k}\vert U \vert$
vertex-disjoint copies of transversal
$\beta ^{\prime }m-\frac{k-1}{k}\vert U \vert$
vertex-disjoint copies of transversal
![]() $C_{k}$
in
$C_{k}$
in
![]() $G[X\backslash V(\mathcal{C}_{1})]$
. This is possible since every vertex
$G[X\backslash V(\mathcal{C}_{1})]$
. This is possible since every vertex
![]() $v$
has at least
$v$
has at least
![]() $k\beta ^{\prime }n-(k-1)\vert U\vert \geq k(\beta ^{\prime }m-\frac{(k-1)}{k}\vert U \vert )$
sets from
$k\beta ^{\prime }n-(k-1)\vert U\vert \geq k(\beta ^{\prime }m-\frac{(k-1)}{k}\vert U \vert )$
sets from
![]() $\mathcal{F}_v$
that are disjoint from
$\mathcal{F}_v$
that are disjoint from
![]() $V(\mathcal{C}_{1})$
. Let
$V(\mathcal{C}_{1})$
. Let
![]() $Q_{i2}\;:\!=\;X_{i}\cap V(\mathcal{C}_{2})$
and
$Q_{i2}\;:\!=\;X_{i}\cap V(\mathcal{C}_{2})$
and
![]() $Q_{i}\;:\!=\;Q_{i1}\cup Q_{i2}$
. Then
$Q_{i}\;:\!=\;Q_{i1}\cup Q_{i2}$
. Then
![]() $Q_i$
is desired because
$Q_i$
is desired because
![]() $\mathcal{C}_{1}\cup \mathcal{C}_{2}$
is indeed a transversal
$\mathcal{C}_{1}\cup \mathcal{C}_{2}$
is indeed a transversal
![]() $C_k$
-factor of
$C_k$
-factor of
![]() $G[\!\bigcup _{i=1}^k Q_i\cup U]$
. This completes the entire proof.
$G[\!\bigcup _{i=1}^k Q_i\cup U]$
. This completes the entire proof.
4.4.3. Proof of Lemma 4.10
Proof of Lemma
4.10. Given
![]() $k \in \mathbb{N}$
with
$k \in \mathbb{N}$
with
![]() $k\geq 4$
and
$k\geq 4$
and
![]() $\delta \gt \frac{2}{k}$
, we set
$\delta \gt \frac{2}{k}$
, we set
![]() $\eta \;:\!=\;\delta -\frac{2}{k}$
and choose
$\eta \;:\!=\;\delta -\frac{2}{k}$
and choose
![]() $\frac{1}{n}\ll \alpha \ll \beta \ll \delta,\eta$
. Let
$\frac{1}{n}\ll \alpha \ll \beta \ll \delta,\eta$
. Let
![]() $G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
$G=(V_{1},\ldots,V_{k},E)$
be a spanning subgraph of the
![]() $n$
-blow-up of
$n$
-blow-up of
![]() $C_{k}$
with
$C_{k}$
with
![]() $\bar{\delta }(G)\geq \delta n$
and
$\bar{\delta }(G)\geq \delta n$
and
![]() $\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
.
$\alpha ^*_{\textrm{b}}(G)\lt \alpha n$
.
Claim 4.13.
For each
![]() $i\in [k]$
,
$i\in [k]$
,
![]() $V_{i}$
is
$V_{i}$
is
![]() $(C_{k},\beta n,2)$
-closed.
$(C_{k},\beta n,2)$
-closed.
Proof of Claim
4.13. Without loss of generality, we may assume that
![]() $i=1$
. For any two vertices
$i=1$
. For any two vertices
![]() $u,v\in V_{1}$
, since
$u,v\in V_{1}$
, since
![]() $\bar{\delta }(G)\geq \delta n$
, we can choose four vertex-disjoint sets
$\bar{\delta }(G)\geq \delta n$
, we can choose four vertex-disjoint sets
![]() $D_{1}$
,
$D_{1}$
,
![]() $D_{2}\subseteq V_{2}$
and
$D_{2}\subseteq V_{2}$
and
![]() $D_{3}, D_{4}\subseteq V_{k}$
each of size at least
$D_{3}, D_{4}\subseteq V_{k}$
each of size at least
![]() $\frac{\delta n}{2}$
such that
$\frac{\delta n}{2}$
such that
![]() $D_{1}\subseteq N_{V_{2}}(u)$
,
$D_{1}\subseteq N_{V_{2}}(u)$
,
![]() $D_{2}\subseteq N_{V_{2}}(v)$
,
$D_{2}\subseteq N_{V_{2}}(v)$
,
![]() $D_{3}\subseteq N_{V_{k}}(u)$
, and
$D_{3}\subseteq N_{V_{k}}(u)$
, and
![]() $D_{4}\subseteq N_{V_{k}}(v)$
, respectively. Given any vertex set
$D_{4}\subseteq N_{V_{k}}(v)$
, respectively. Given any vertex set
![]() $W\subseteq V(G)\backslash \left \{u,v \right \}$
of size at most
$W\subseteq V(G)\backslash \left \{u,v \right \}$
of size at most
![]() $\beta n$
, let
$\beta n$
, let
![]() $V^{\prime }_{i}=V_{i}\backslash W$
and
$V^{\prime }_{i}=V_{i}\backslash W$
and
![]() $D^{\prime }_{j}=D_{j}\backslash W$
for
$D^{\prime }_{j}=D_{j}\backslash W$
for
![]() $i\in [k]$
and
$i\in [k]$
and
![]() $j\in [4]$
. Note that
$j\in [4]$
. Note that
![]() $\vert V^{\prime }_{i}\vert \geq n-\beta n\geq 10\alpha n$
and
$\vert V^{\prime }_{i}\vert \geq n-\beta n\geq 10\alpha n$
and
![]() $\vert D^{\prime }_{j}\vert \geq \frac{\delta n}{2}-\beta n\geq \alpha n$
.
$\vert D^{\prime }_{j}\vert \geq \frac{\delta n}{2}-\beta n\geq \alpha n$
.
Since
![]() $\alpha ^*_{\textrm{b}}(G)\lt \alpha n\leq \vert D_{j}^{\prime }\vert, \vert V^{\prime }_{1}\vert$
, there exist subsets
$\alpha ^*_{\textrm{b}}(G)\lt \alpha n\leq \vert D_{j}^{\prime }\vert, \vert V^{\prime }_{1}\vert$
, there exist subsets
![]() $S_{j}\subseteq V^{\prime }_{1}$
of size at least
$S_{j}\subseteq V^{\prime }_{1}$
of size at least
![]() $\vert V^{\prime }_{1}\vert -\alpha n$
such that every vertex in
$\vert V^{\prime }_{1}\vert -\alpha n$
such that every vertex in
![]() $S_{j}$
has at least one neighbour inside
$S_{j}$
has at least one neighbour inside
![]() $D_{j}^{\prime }$
. By the fact that
$D_{j}^{\prime }$
. By the fact that
![]() $\vert S_{j}\vert \geq \vert V^{\prime }_{1}\vert -\alpha n\gt \frac{3}{4}\vert V^{\prime }_{1}\vert$
, we have that
$\vert S_{j}\vert \geq \vert V^{\prime }_{1}\vert -\alpha n\gt \frac{3}{4}\vert V^{\prime }_{1}\vert$
, we have that
![]() $S\;:\!=\;\bigcap _{j=1}^{4}S_{j}\neq \emptyset$
. Arbitrarily choose
$S\;:\!=\;\bigcap _{j=1}^{4}S_{j}\neq \emptyset$
. Arbitrarily choose
![]() $x\in S$
, and therefore there exist vertices
$x\in S$
, and therefore there exist vertices
![]() $y_{1}$
,
$y_{1}$
,
![]() $y_{2}$
,
$y_{2}$
,
![]() $y_{3}$
,
$y_{3}$
,
![]() $y_{4}$
satisfying
$y_{4}$
satisfying
![]() $y_{i}\in N_{D_{i}^{\prime }}(x)$
for
$y_{i}\in N_{D_{i}^{\prime }}(x)$
for
![]() $i\in [k]$
. Note that
$i\in [k]$
. Note that
![]() $\vert N_{V^{\prime }_{3}}(y_{1})\vert$
,
$\vert N_{V^{\prime }_{3}}(y_{1})\vert$
,
![]() $\vert N_{V^{\prime }_{k-1}}(y_{3})\vert \geq \delta n-\beta n\geq \alpha n$
and
$\vert N_{V^{\prime }_{k-1}}(y_{3})\vert \geq \delta n-\beta n\geq \alpha n$
and
![]() $\vert V^{\prime }_{i}\vert \geq 10\alpha n$
for
$\vert V^{\prime }_{i}\vert \geq 10\alpha n$
for
![]() $i\in [k]$
. When
$i\in [k]$
. When
![]() $k\gt 4$
, by applying Proposition 4.7 with
$k\gt 4$
, by applying Proposition 4.7 with
![]() $X_{i}\;:\!=\;N_{V^{\prime }_{3}}(y_{1})$
and
$X_{i}\;:\!=\;N_{V^{\prime }_{3}}(y_{1})$
and
![]() $X_{j}\;:\!=\;N_{V^{\prime }_{k-1}}(y_{3})$
, we can obtain a transversal cycle
$X_{j}\;:\!=\;N_{V^{\prime }_{k-1}}(y_{3})$
, we can obtain a transversal cycle
![]() $C_{1}$
passing through
$C_{1}$
passing through
![]() $u, y_{1}, y_{3}$
. When
$u, y_{1}, y_{3}$
. When
![]() $k=4$
, since
$k=4$
, since
![]() $\vert N_{V^{\prime }_{3}}(y_{1})\vert$
,
$\vert N_{V^{\prime }_{3}}(y_{1})\vert$
,
![]() $\vert N_{V^{\prime }_{3}}(y_{3})\vert \geq \delta n-\beta n\geq (\frac{1}{2}+\eta -\beta ) n\gt \frac{n}{2}$
, we can easily find a common neighbour of
$\vert N_{V^{\prime }_{3}}(y_{3})\vert \geq \delta n-\beta n\geq (\frac{1}{2}+\eta -\beta ) n\gt \frac{n}{2}$
, we can easily find a common neighbour of
![]() $y_{1}, y_{3}$
and thus obtain a transversal cycle
$y_{1}, y_{3}$
and thus obtain a transversal cycle
![]() $C_{1}$
passing through
$C_{1}$
passing through
![]() $u, y_{1}, y_{3}$
. Similarly, we can obtain a transversal cycle
$u, y_{1}, y_{3}$
. Similarly, we can obtain a transversal cycle
![]() $C_{2}$
in
$C_{2}$
in
![]() $V(G)\backslash (W\cup V(C_{1}))$
that passes through
$V(G)\backslash (W\cup V(C_{1}))$
that passes through
![]() $v, y_{2}, y_{4}$
. In fact, the set
$v, y_{2}, y_{4}$
. In fact, the set
![]() $\left \{ x \right \}\cup \left (V(C_{1})\backslash \left \{ u \right \}\right )\cup \left (V(C_{2})\backslash \left \{ v \right \}\right )$
is a
$\left \{ x \right \}\cup \left (V(C_{1})\backslash \left \{ u \right \}\right )\cup \left (V(C_{2})\backslash \left \{ v \right \}\right )$
is a
![]() $C_{k}$
-connector for
$C_{k}$
-connector for
![]() $u$
,
$u$
,
![]() $v$
. Therefore by definition,
$v$
. Therefore by definition,
![]() $u$
is
$u$
is
![]() $(C_{k},\beta n,2)$
-reachable to
$(C_{k},\beta n,2)$
-reachable to
![]() $v$
.
$v$
.
For every transversal
![]() $k$
-subset
$k$
-subset
![]() $S\subseteq V(G)$
, we greedily find as many pairwise disjoint
$S\subseteq V(G)$
, we greedily find as many pairwise disjoint
![]() $(C_{k},2k)$
-absorbers for
$(C_{k},2k)$
-absorbers for
![]() $S$
as possible. For convenience, we write
$S$
as possible. For convenience, we write
![]() $S=\left \{ s_{1}, s_{2},\ldots,s_{k} \right \}$
where
$S=\left \{ s_{1}, s_{2},\ldots,s_{k} \right \}$
where
![]() $s_{i}\in V_{i}$
for
$s_{i}\in V_{i}$
for
![]() $i\in [k]$
. Let
$i\in [k]$
. Let
![]() $\mathcal{A}=\left \{ A_{1}, A_{2},\ldots,A_{\ell } \right \}$
be a maximal family of such absorbers. Suppose to the contrary that
$\mathcal{A}=\left \{ A_{1}, A_{2},\ldots,A_{\ell } \right \}$
be a maximal family of such absorbers. Suppose to the contrary that
![]() $\ell \lt \frac{\beta n-k}{4k^2}$
. Since each
$\ell \lt \frac{\beta n-k}{4k^2}$
. Since each
![]() $A_{j}$
has size at most
$A_{j}$
has size at most
![]() $2k^2$
, we have
$2k^2$
, we have
![]() $\left \vert \bigcup _{j=1}^{\ell }A_{j}\right \vert \lt \frac{\beta n-k}{2}$
.
$\left \vert \bigcup _{j=1}^{\ell }A_{j}\right \vert \lt \frac{\beta n-k}{2}$
.
Since
![]() $\alpha \ll \beta \ll \delta$
, we can easily find a copy
$\alpha \ll \beta \ll \delta$
, we can easily find a copy
![]() $T$
of transversal
$T$
of transversal
![]() $C_{k}$
in
$C_{k}$
in
![]() $V(G)\backslash (\bigcup _{j=1}^{\ell }A_{j}\cup S)$
and write
$V(G)\backslash (\bigcup _{j=1}^{\ell }A_{j}\cup S)$
and write
![]() $T=\left \{ t_{1}, t_{2},\ldots,t_{k} \right \}$
where
$T=\left \{ t_{1}, t_{2},\ldots,t_{k} \right \}$
where
![]() $t_{i}\in V_{i}$
for
$t_{i}\in V_{i}$
for
![]() $i\in [k]$
. By the closedness of
$i\in [k]$
. By the closedness of
![]() $V_{i}$
, we can pick a collection
$V_{i}$
, we can pick a collection
![]() $\left \{ I_{1}, I_{2},\ldots,I_{k} \right \}$
of vertex-disjoint subsets in
$\left \{ I_{1}, I_{2},\ldots,I_{k} \right \}$
of vertex-disjoint subsets in
![]() $V(G)\backslash (\bigcup _{j=1}^{\ell }A_{j}\cup S\cup T)$
such that each
$V(G)\backslash (\bigcup _{j=1}^{\ell }A_{j}\cup S\cup T)$
such that each
![]() $I_{i}$
is a
$I_{i}$
is a
![]() $C_{k}$
-connector for
$C_{k}$
-connector for
![]() $s_{i}$
,
$s_{i}$
,
![]() $t_{i}$
with
$t_{i}$
with
![]() $\vert I_{i} \vert \leq 2k-1$
. In fact, for any
$\vert I_{i} \vert \leq 2k-1$
. In fact, for any
![]() $1\leq k^{\prime }\leq k$
, we have
$1\leq k^{\prime }\leq k$
, we have
 \begin{equation*} \left \vert \bigcup _{j=1}^{\ell }A_{j}\cup \left (\bigcup _{i=1}^{k^{\prime }}I_{i}\right )\cup S\cup T\right \vert \leq \frac{\beta n-k}{2}+k(2k-1)+2k\lt \beta n. \end{equation*}
\begin{equation*} \left \vert \bigcup _{j=1}^{\ell }A_{j}\cup \left (\bigcup _{i=1}^{k^{\prime }}I_{i}\right )\cup S\cup T\right \vert \leq \frac{\beta n-k}{2}+k(2k-1)+2k\lt \beta n. \end{equation*}
Therefore, we can choose such
![]() $I_{i}$
one by one because
$I_{i}$
one by one because
![]() $s_{i}$
and
$s_{i}$
and
![]() $t_{i}$
are
$t_{i}$
are
![]() $(C_{k},\beta n,2)$
-reachable. At this point, it is easy to verify that
$(C_{k},\beta n,2)$
-reachable. At this point, it is easy to verify that
![]() $\bigcup _{i=1}^{k} I_{i}\cup T$
is actually a
$\bigcup _{i=1}^{k} I_{i}\cup T$
is actually a
![]() $(C_{k},2k)$
-absorber for
$(C_{k},2k)$
-absorber for
![]() $S$
, contrary to the maximality of
$S$
, contrary to the maximality of
![]() $\ell$
.
$\ell$
.
Acknowledgements
We would like to thank the anonymous referees for their thorough reading of the manuscript and many helpful suggestions.