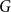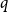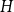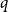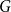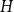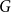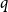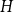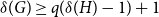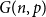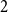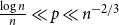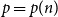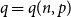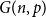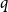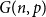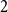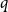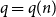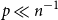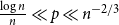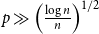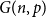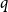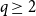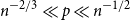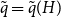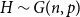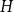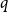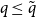1. Introduction
1.1. Minimum degrees of minimal Ramsey graphs
We say that a graph
![]() $G$
is
$G$
is
![]() $q$
-Ramsey for another graph
$q$
-Ramsey for another graph
![]() $H$
, and write
$H$
, and write
![]() $G\to _q H$
, if, for any
$G\to _q H$
, if, for any
![]() $q$
-colouring of the edges of
$q$
-colouring of the edges of
![]() $G$
, there exists a monochromatic copy of
$G$
, there exists a monochromatic copy of
![]() $H$
, that is, a copy of
$H$
, that is, a copy of
![]() $H$
whose edges all have the same colour. The fundamental theorem of Ramsey [Reference Ramsey1] asserts that
$H$
whose edges all have the same colour. The fundamental theorem of Ramsey [Reference Ramsey1] asserts that
![]() $K_n \rightarrow _q H$
for sufficiently large
$K_n \rightarrow _q H$
for sufficiently large
![]() $n$
, and hence at least one such graph
$n$
, and hence at least one such graph
![]() $G$
exists for any choice of
$G$
exists for any choice of
![]() $H$
and
$H$
and
![]() $q$
. It is then natural to investigate the nature of graphs
$q$
. It is then natural to investigate the nature of graphs
![]() $G$
that are
$G$
that are
![]() $q$
-Ramsey for a given graph
$q$
-Ramsey for a given graph
![]() $H$
. As a first step in this direction, we can ask how large such a graph
$H$
. As a first step in this direction, we can ask how large such a graph
![]() $G$
needs to be, leading us to the definition of the most well-studied concept related to Ramsey graphs, the Ramsey number. In this language, the
$G$
needs to be, leading us to the definition of the most well-studied concept related to Ramsey graphs, the Ramsey number. In this language, the
![]() $q$
-colour Ramsey number of a graph
$q$
-colour Ramsey number of a graph
![]() $H$
, denoted
$H$
, denoted
![]() $r_q(H)$
, is defined as the minimum number of vertices in a graph that is
$r_q(H)$
, is defined as the minimum number of vertices in a graph that is
![]() $q$
-Ramsey for
$q$
-Ramsey for
![]() $H$
. Over the past few decades, this parameter has been studied extensively for various choices of the graph
$H$
. Over the past few decades, this parameter has been studied extensively for various choices of the graph
![]() $H$
. Arguably the most important case is when
$H$
. Arguably the most important case is when
![]() $H$
is a complete graph. It was shown by Erdős [Reference Erdős2] and Erdős and Szekeres [Reference Erdős and Szekeres3] that
$H$
is a complete graph. It was shown by Erdős [Reference Erdős2] and Erdős and Szekeres [Reference Erdős and Szekeres3] that
![]() $r_2(K_t)$
is exponential in
$r_2(K_t)$
is exponential in
![]() $t$
; more precisely, they proved that
$t$
; more precisely, they proved that
![]() $2^{t/2}\leq r_2(K_t) \leq 2^{2t}$
. Despite decades of continuous effort, the first improvement in the bases of these exponential bounds came only in 2023, when Campos, Griffiths, Morris, and Sahasrabudhe [Reference Campos4] announced an upper bound of
$2^{t/2}\leq r_2(K_t) \leq 2^{2t}$
. Despite decades of continuous effort, the first improvement in the bases of these exponential bounds came only in 2023, when Campos, Griffiths, Morris, and Sahasrabudhe [Reference Campos4] announced an upper bound of
![]() $({4 - \varepsilon })^t$
(subsequently optimised by Gupta, Ndiaye, Norin, and Wei [Reference Gupta, Ndiaye, Norin and Wei5]). Prior to this breakthrough, all improvements had been in the lower-order terms, with Sah [Reference Sah6] building on previous work of Conlon [Reference Conlon7] to reduce the upper bound by a superpolynomial factor; from below, Spencer [Reference Spencer8] proved the best known lower bound, a mere factor of two larger than the original bound of Erdős.
$({4 - \varepsilon })^t$
(subsequently optimised by Gupta, Ndiaye, Norin, and Wei [Reference Gupta, Ndiaye, Norin and Wei5]). Prior to this breakthrough, all improvements had been in the lower-order terms, with Sah [Reference Sah6] building on previous work of Conlon [Reference Conlon7] to reduce the upper bound by a superpolynomial factor; from below, Spencer [Reference Spencer8] proved the best known lower bound, a mere factor of two larger than the original bound of Erdős.
In a bid to better understand the Ramsey property, researchers began exploring other parameters of Ramsey graphs in the 1970s, and we shall be interested in the minimum degree, the study of which began with the paper of Burr, Erdős, and Lovász [Reference Burr, Erdős and Lovász9]. Of course, since any supergraph of a
![]() $q$
-Ramsey graph for
$q$
-Ramsey graph for
![]() $H$
is itself
$H$
is itself
![]() $q$
-Ramsey for
$q$
-Ramsey for
![]() $H$
, the question of determining the smallest possible minimum degree among all
$H$
, the question of determining the smallest possible minimum degree among all
![]() $q$
-Ramsey graphs for
$q$
-Ramsey graphs for
![]() $H$
is rather uninteresting: we can always add an isolated vertex and make the minimum degree zero. To avoid such trivialities, we restrict our attention to the subcollection
$H$
is rather uninteresting: we can always add an isolated vertex and make the minimum degree zero. To avoid such trivialities, we restrict our attention to the subcollection
![]() $\mathcal{M}_q(H)$
of minimal Ramsey graphs. We say that
$\mathcal{M}_q(H)$
of minimal Ramsey graphs. We say that
![]() $G$
is a minimal
$G$
is a minimal
![]() $q$
-Ramsey graph for
$q$
-Ramsey graph for
![]() $H$
if
$H$
if
![]() $G$
is
$G$
is
![]() $q$
-Ramsey for
$q$
-Ramsey for
![]() $H$
and contains no proper subgraph with this property. In other words, removing any edge or vertex destroys the Ramsey property of the graph. We can then define the parameter
$H$
and contains no proper subgraph with this property. In other words, removing any edge or vertex destroys the Ramsey property of the graph. We can then define the parameter
![]() $s_q(H)$
, introduced in [Reference Burr, Erdős and Lovász9] for
$s_q(H)$
, introduced in [Reference Burr, Erdős and Lovász9] for
![]() $q=2$
, as the smallest minimum degree among all minimal
$q=2$
, as the smallest minimum degree among all minimal
![]() $q$
-Ramsey graphs for
$q$
-Ramsey graphs for
![]() $H$
, that is,
$H$
, that is,
where as usual
![]() $\delta (G)$
denotes the minimum degree of
$\delta (G)$
denotes the minimum degree of
![]() $G$
.
$G$
.
When studying this parameter, there are a couple of easy general bounds one can give. For an upper bound, observe that since, by definition,
![]() $K_{r_q(H)} \rightarrow _q H$
, any minimal
$K_{r_q(H)} \rightarrow _q H$
, any minimal
![]() $q$
-Ramsey subgraph of this complete graph bears witness to the fact that
$q$
-Ramsey subgraph of this complete graph bears witness to the fact that
![]() $s_q(H) \le r_q(H) - 1$
. From below, as observed by Fox and Lin [Reference Fox and Lin10], a simple argument using the pigeonhole principle shows that
$s_q(H) \le r_q(H) - 1$
. From below, as observed by Fox and Lin [Reference Fox and Lin10], a simple argument using the pigeonhole principle shows that
![]() $s_q(H) \ge q(\delta (H) - 1) + 1$
. Note that these bounds are typically very far apart: when
$s_q(H) \ge q(\delta (H) - 1) + 1$
. Note that these bounds are typically very far apart: when
![]() $H = K_t$
, for instance, the lower bound is linear in
$H = K_t$
, for instance, the lower bound is linear in
![]() $t$
while the upper bound is exponential.
$t$
while the upper bound is exponential.
In their original paper, Burr, Erdős, and Lovász [Reference Burr, Erdős and Lovász9] showed that
![]() $s_2(K_t) = (t-1)^2$
, a surprising result for two reasons. First, while the two-colour Ramsey number of
$s_2(K_t) = (t-1)^2$
, a surprising result for two reasons. First, while the two-colour Ramsey number of
![]() $K_t$
is still unknown for any
$K_t$
is still unknown for any
![]() $t \ge 5$
, we can determine
$t \ge 5$
, we can determine
![]() $s_2(K_t)$
precisely for every
$s_2(K_t)$
precisely for every
![]() $t$
. Second,
$t$
. Second,
![]() $s_2(K_t)$
is significantly smaller than
$s_2(K_t)$
is significantly smaller than
![]() $r_2(K_t)$
. Informally, this means that a large Ramsey graph for
$r_2(K_t)$
. Informally, this means that a large Ramsey graph for
![]() $K_t$
can have a vertex of very low degree whose removal destroys the Ramsey property.
$K_t$
can have a vertex of very low degree whose removal destroys the Ramsey property.
Since its introduction in [Reference Burr, Erdős and Lovász9], the parameter
![]() $s_q(H)$
has been studied for a number of different choices of
$s_q(H)$
has been studied for a number of different choices of
![]() $H$
and for larger
$H$
and for larger
![]() $q$
; see, for example, [Reference Fox and Lin10–Reference Szabó, Zumstein and Zürcher20]. To the best of our knowledge, in all cases studied the value of
$q$
; see, for example, [Reference Fox and Lin10–Reference Szabó, Zumstein and Zürcher20]. To the best of our knowledge, in all cases studied the value of
![]() $s_q(H)$
is far away from the trivial upper bound. On the other hand, the lower bound of Fox and Lin [Reference Fox and Lin10] has been shown to be tight for many graphs. Following Grinshpun [Reference Grinshpun17], we call such graphs
$s_q(H)$
is far away from the trivial upper bound. On the other hand, the lower bound of Fox and Lin [Reference Fox and Lin10] has been shown to be tight for many graphs. Following Grinshpun [Reference Grinshpun17], we call such graphs
![]() $q$
-Ramsey simple.
$q$
-Ramsey simple.
Definition 1.1.
A graph
![]() $H$
without isolated vertices is said to be
$H$
without isolated vertices is said to be
![]() $q$
-Ramsey simple if
$q$
-Ramsey simple if
If
![]() $H$
has isolated vertices, then we say that
$H$
has isolated vertices, then we say that
![]() $H$
is
$H$
is
![]() $q$
-Ramsey simple if the graph obtained from
$q$
-Ramsey simple if the graph obtained from
![]() $H$
by removing all isolated vertices is
$H$
by removing all isolated vertices is
![]() $q$
-Ramsey simple.
$q$
-Ramsey simple.
Observe that adding isolated vertices to a graph does not affect the structure of the corresponding Ramsey graphs significantly. Indeed, if
![]() $H$
is a graph without isolated vertices and
$H$
is a graph without isolated vertices and
![]() $H + tK_1$
is the graph obtained from
$H + tK_1$
is the graph obtained from
![]() $H$
by adding
$H$
by adding
![]() $t \ge 0$
isolated vertices, it is not difficult to check that
$t \ge 0$
isolated vertices, it is not difficult to check that
![]() $G \in \mathcal{M}_q(H)$
if and only if
$G \in \mathcal{M}_q(H)$
if and only if
![]() $G + sK_1 \in \mathcal{M}_q(H + tK_1)$
, where
$G + sK_1 \in \mathcal{M}_q(H + tK_1)$
, where
![]() $s = \max \{0, t- (v(G) - v(H))\}$
.
$s = \max \{0, t- (v(G) - v(H))\}$
.
Previous work by Fox and Lin [Reference Fox and Lin10], Szabó, Zumstein, and Zürcher [Reference Szabó, Zumstein and Zürcher20], and Grinshpun [Reference Grinshpun17] has established the
![]() $2$
-Ramsey simplicity of a wide range of bipartite graphs. Further results were proven in [Reference Boyadzhiyska, Clemens and Gupta13], including the
$2$
-Ramsey simplicity of a wide range of bipartite graphs. Further results were proven in [Reference Boyadzhiyska, Clemens and Gupta13], including the
![]() $q$
-Ramsey simplicity of all cycles of length at least four, for any number of colours
$q$
-Ramsey simplicity of all cycles of length at least four, for any number of colours
![]() $q \ge 2$
. Based on these results, it is believed that simplicity is a more widespread phenomenon.
$q \ge 2$
. Based on these results, it is believed that simplicity is a more widespread phenomenon.
Conjecture 1.2 (Szabó, Zumstein, and Zürcher [Reference Szabó, Zumstein and Zürcher20]). Every bipartite graph is
![]() $2$
-Ramsey simple.
$2$
-Ramsey simple.
The conjecture suggests that Ramsey simplicity is quite common, but it is natural to wonder whether this extends beyond the bipartite setting. We know that cliques are not simple, but are they an exceptional case, or is
![]() $q$
-Ramsey simplicity atypical for non-bipartite graphs? For a more concrete question, when can we expect the
$q$
-Ramsey simplicity atypical for non-bipartite graphs? For a more concrete question, when can we expect the
![]() $n$
-vertex binomial random graph
$n$
-vertex binomial random graph
![]() $G(n,p)$
, where every edge appears independently with probability
$G(n,p)$
, where every edge appears independently with probability
![]() $p$
, to be
$p$
, to be
![]() $q$
-Ramsey simple?
$q$
-Ramsey simple?
1.2. Random graphs
Random graphs have long played an important role in Ramsey Theory: Erdős’s famous exponential lower bound on the Ramsey numbers of complete graphs in [Reference Erdős2] came from analysing the clique and independence numbers of random graphs, while a key ingredient in the best modern upper bounds is showing that graphs without large cliques or independent sets must be random-like. When it comes to more general Ramsey problems, the work of Rödl and Ruciński [Reference Rödl and Ruciński21, Reference Rödl and Ruciński22] establishes, for a given graph
![]() $H$
and number of colours
$H$
and number of colours
![]() $q$
, the range of values of
$q$
, the range of values of
![]() $p$
for which we have
$p$
for which we have
![]() $G(n,p) \rightarrow _q H$
with high probability.
$G(n,p) \rightarrow _q H$
with high probability.
In these seminal papers, which have inspired a great deal of subsequent research, the random graph plays the role of the host graph
![]() $G$
, while the target graph
$G$
, while the target graph
![]() $H$
is fixed in advance. Surprisingly, there has been considerably less work in the setting where the target graph
$H$
is fixed in advance. Surprisingly, there has been considerably less work in the setting where the target graph
![]() $H$
is itself random. When
$H$
is itself random. When
![]() $H \sim G(n,p)$
, Fox and Sudakov [Reference Fox and Sudakov23] and Conlon [Reference Conlon24] provided some lower and upper bounds on
$H \sim G(n,p)$
, Fox and Sudakov [Reference Fox and Sudakov23] and Conlon [Reference Conlon24] provided some lower and upper bounds on
![]() $r_2(H)$
for different ranges of
$r_2(H)$
for different ranges of
![]() $p$
, while Conlon, Fox, and Sudakov [Reference Conlon, Fox and Sudakov25] showed that
$p$
, while Conlon, Fox, and Sudakov [Reference Conlon, Fox and Sudakov25] showed that
![]() $\log r_2(H)$
is well concentrated.
$\log r_2(H)$
is well concentrated.
In this paper we shall focus on the minimum degree of Ramsey graphs for the random graph
![]() $G(n,p)$
, with the goal of determining when it is
$G(n,p)$
, with the goal of determining when it is
![]() $q$
-Ramsey simple. This line of research was initiated by Grinshpun [Reference Grinshpun17], who proved that sparse random graphs are 2-Ramsey simple with high probability.
$q$
-Ramsey simple. This line of research was initiated by Grinshpun [Reference Grinshpun17], who proved that sparse random graphs are 2-Ramsey simple with high probability.
Theorem 1.3 (Corollary 2.1.4 in [Reference Grinshpun17]). Let
![]() $p=p(n)\in (0,1)$
and
$p=p(n)\in (0,1)$
and
![]() $H\sim G(n,p)$
. If
$H\sim G(n,p)$
. If
![]() $\frac{\log n}{n}\ll p \ll n^{-2/3}$
, then a.a.s.
$\frac{\log n}{n}\ll p \ll n^{-2/3}$
, then a.a.s.
![]() $H$
is
$H$
is
![]() $2$
-Ramsey simple.
$2$
-Ramsey simple.
In this range of edge probabilities the random graph is almost surely not bipartite (in fact, its chromatic number is unbounded), showing that Conjecture 1.2 does not tell the full story. Moreover, the argument in [Reference Grinshpun17] can easily be extended to prove, for any fixed
![]() $q \in \mathbb{N}$
,
$q \in \mathbb{N}$
,
![]() $q$
-Ramsey simplicity for
$q$
-Ramsey simplicity for
![]() $G(n,p)$
in the above range of
$G(n,p)$
in the above range of
![]() $p$
. This begs two natural questions: what happens when the number of colours
$p$
. This begs two natural questions: what happens when the number of colours
![]() $q$
grows with
$q$
grows with
![]() $n$
, and what happens in other ranges of the edge probability
$n$
, and what happens in other ranges of the edge probability
![]() $p$
?
$p$
?
1.3. Results
In this paper, we settle this question for a wide range of parameters, uncovering some unexpected behaviour in the process. Our main result qualitatively describes the Ramsey simplicity of the random graph
![]() $G(n,p)$
as the edge probability
$G(n,p)$
as the edge probability
![]() $p$
grows.
$p$
grows.
Theorem 1.4.
Let
![]() $p = p(n) \in (0,1)$
and
$p = p(n) \in (0,1)$
and
![]() $H \sim G(n,p)$
. Then the following statements hold asymptotically almost surely.
$H \sim G(n,p)$
. Then the following statements hold asymptotically almost surely.
-
(a) If
 $0 \lt p \ll n^{-1}$
or
$0 \lt p \ll n^{-1}$
or
 $\frac{\log n}{n} \ll p \ll n^{-\frac 23}$
, then
$\frac{\log n}{n} \ll p \ll n^{-\frac 23}$
, then
 $H$
is
$H$
is
 $q$
-Ramsey simple for all
$q$
-Ramsey simple for all
 $q = q(n)$
.
$q = q(n)$
. -
(b) If
 $n^{-\frac 23} \ll p \ll n^{-\frac 12}$
, there is some finite
$n^{-\frac 23} \ll p \ll n^{-\frac 12}$
, there is some finite
 $\tilde{q}(H)$
such that
$\tilde{q}(H)$
such that
 $H$
is
$H$
is
 $q$
-Ramsey simple if and only if
$q$
-Ramsey simple if and only if
 $q \le \tilde{q}(H)$
.
$q \le \tilde{q}(H)$
. -
(c) If
 $\left ( \frac{\log n}{n} \right )^{\frac 12} \ll p \lt 1$
, then
$\left ( \frac{\log n}{n} \right )^{\frac 12} \ll p \lt 1$
, then
 $H$
is not
$H$
is not
 $q$
-Ramsey simple for any
$q$
-Ramsey simple for any
 $q \ge 2$
.
$q \ge 2$
.
There are a few comments to be made at this point. First, observe that these results suggest some monotonicity in
![]() $q$
– in parts (a), (b), and (c), we have that, if
$q$
– in parts (a), (b), and (c), we have that, if
![]() $H$
is
$H$
is
![]() $q$
-Ramsey simple, then it is also
$q$
-Ramsey simple, then it is also
![]() $(q-1)$
-Ramsey simple. This is in fact a general phenomenon, true for all graphs
$(q-1)$
-Ramsey simple. This is in fact a general phenomenon, true for all graphs
![]() $H$
and all numbers of colours
$H$
and all numbers of colours
![]() $q$
, and we shall show this in Section 2. Given this monotone behaviour, we define the Ramsey simplicity threshold
$q$
, and we shall show this in Section 2. Given this monotone behaviour, we define the Ramsey simplicity threshold
for every graph
![]() $H$
. Note that every graph is, by definition,
$H$
. Note that every graph is, by definition,
![]() $1$
-Ramsey simple, since the only minimal
$1$
-Ramsey simple, since the only minimal
![]() $1$
-Ramsey graph for
$1$
-Ramsey graph for
![]() $H$
is
$H$
is
![]() $H$
itself, and so
$H$
itself, and so
![]() $s_1(H) = \delta (H)$
. Thus, when a graph
$s_1(H) = \delta (H)$
. Thus, when a graph
![]() $H$
is not
$H$
is not
![]() $q$
-Ramsey simple for any number of colours
$q$
-Ramsey simple for any number of colours
![]() $q \ge 2$
, we have
$q \ge 2$
, we have
![]() $\tilde{q}(H) = 1$
. At the other extreme, if
$\tilde{q}(H) = 1$
. At the other extreme, if
![]() $H$
is
$H$
is
![]() $q$
-Ramsey simple for any number of colours
$q$
-Ramsey simple for any number of colours
![]() $q$
, we have
$q$
, we have
![]() $\tilde{q}(H) = \infty$
.
$\tilde{q}(H) = \infty$
.
On the other hand, as we shall also remark in Section 2, we do not have monotonicity in
![]() $H$
. Indeed, a Ramsey simple graph can have subgraphs and supergraphs that are not Ramsey simple, and vice versa. However, Theorem1.4 shows that in the random graph, there is some large-scale negative correlation between the density of the graph and its Ramsey simplicity. That is, part (a) shows that very sparse random graphs are always Ramsey simple, while (c) asserts that somewhat denser random graphs are never Ramsey simple.
$H$
. Indeed, a Ramsey simple graph can have subgraphs and supergraphs that are not Ramsey simple, and vice versa. However, Theorem1.4 shows that in the random graph, there is some large-scale negative correlation between the density of the graph and its Ramsey simplicity. That is, part (a) shows that very sparse random graphs are always Ramsey simple, while (c) asserts that somewhat denser random graphs are never Ramsey simple.
Meanwhile, part (b) shows that random graphs of intermediate density lie somewhere between these two extremes, as they are simple when we have few colours and not simple when we have many. We shall in fact prove a more precise version of this theorem (see Theorem5.1), which shows that the Ramsey simplicity of
![]() $H$
is essentially determined by the subgraph
$H$
is essentially determined by the subgraph
![]() $F$
induced by the neighbourhood of the vertex of minimum degree, and will give lower and upper bounds on
$F$
induced by the neighbourhood of the vertex of minimum degree, and will give lower and upper bounds on
![]() $\tilde{q}(H)$
in terms of
$\tilde{q}(H)$
in terms of
![]() $F$
. By analysing the random graph, we can then give quantitative bounds on
$F$
. By analysing the random graph, we can then give quantitative bounds on
![]() $\tilde{q}(H)$
in this middle range.
$\tilde{q}(H)$
in this middle range.
Corollary 1.5.
Let
![]() $k \ge 2$
be a fixed integer, let
$k \ge 2$
be a fixed integer, let
![]() $n^{-\frac{k}{2k-1}} \ll p \ll n^{-\frac{k+1}{2k+1}}$
, and let
$n^{-\frac{k}{2k-1}} \ll p \ll n^{-\frac{k+1}{2k+1}}$
, and let
![]() $H \sim G(n,p)$
. Then, asymptotically almost surely, we have
$H \sim G(n,p)$
. Then, asymptotically almost surely, we have
This corollary determines the threshold
![]() $\tilde{q}(H)$
– the largest number of colours for which
$\tilde{q}(H)$
– the largest number of colours for which
![]() $H$
is
$H$
is
![]() $q$
-Ramsey simple – up to a constant factor, and shows that its small-scale behaviour is quite different from its large-scale behaviour. Indeed, while Theorem1.4 shows
$q$
-Ramsey simple – up to a constant factor, and shows that its small-scale behaviour is quite different from its large-scale behaviour. Indeed, while Theorem1.4 shows
![]() $\tilde{q}(H)$
decreases from infinity to
$\tilde{q}(H)$
decreases from infinity to
![]() $1$
as
$1$
as
![]() $p$
increases from
$p$
increases from
![]() $\frac{\log n}{n}$
to
$\frac{\log n}{n}$
to
![]() $\left ( \frac{\log n }{ n } \right )^{\frac 12}$
, Corollary 1.5 shows that
$\left ( \frac{\log n }{ n } \right )^{\frac 12}$
, Corollary 1.5 shows that
![]() $\tilde{q}(H)$
grows as
$\tilde{q}(H)$
grows as
![]() $p$
goes from
$p$
goes from
![]() $n^{-\frac{k}{2k-1}}$
to
$n^{-\frac{k}{2k-1}}$
to
![]() $n^{-\frac{k+1}{2k+1}}$
, for each fixed
$n^{-\frac{k+1}{2k+1}}$
, for each fixed
![]() $k \ge 2$
. Thus, the overall decrease of
$k \ge 2$
. Thus, the overall decrease of
![]() $\tilde{q}(H)$
cannot be monotone in
$\tilde{q}(H)$
cannot be monotone in
![]() $p$
, as illustrated in Figure 1. Note that a more precise version of the above statement can be found in Corollary 5.2.
$p$
, as illustrated in Figure 1. Note that a more precise version of the above statement can be found in Corollary 5.2.

Figure 1. Bounds on the simplicity threshold
![]() $\tilde{q}(G(n,p))$
.
$\tilde{q}(G(n,p))$
.
Our proofs shed some light on why this phenomenon occurs. We show in Section 3 that if we write
![]() $F$
for the subgraph of
$F$
for the subgraph of
![]() $H$
induced by the neighbourhood of its minimum degree vertex, then
$H$
induced by the neighbourhood of its minimum degree vertex, then
![]() $H$
being
$H$
being
![]() $q$
-Ramsey simple is essentially equivalent to being able to pack
$q$
-Ramsey simple is essentially equivalent to being able to pack
![]() $q$
edge-disjoint copies of
$q$
edge-disjoint copies of
![]() $F$
on a set of
$F$
on a set of
![]() $q(\delta (H) - 1) + 1$
vertices. For fixed
$q(\delta (H) - 1) + 1$
vertices. For fixed
![]() $k$
, as
$k$
, as
![]() $p$
increases from
$p$
increases from
![]() $n^{-\frac{k}{2k-1}}$
to
$n^{-\frac{k}{2k-1}}$
to
![]() $n^{-\frac{k+1}{2k+1}}$
, the minimum degree of
$n^{-\frac{k+1}{2k+1}}$
, the minimum degree of
![]() $H$
grows, and so the order of
$H$
grows, and so the order of
![]() $F$
increases. However, the complexity of
$F$
increases. However, the complexity of
![]() $F$
does not – the order of its largest component remains
$F$
does not – the order of its largest component remains
![]() $k$
. Thus, we have more space to work with, while the packing does not become much harder, which affords us the flexibility to pack more copies of
$k$
. Thus, we have more space to work with, while the packing does not become much harder, which affords us the flexibility to pack more copies of
![]() $F$
.
$F$
.
1.4. Organisation and notation
In Section 2, we discuss the monotonicity of Ramsey simplicity and shall in particular justify the existence of the Ramsey simplicity threshold
![]() $\tilde{q}(H)$
. We then discuss general necessary and sufficient conditions for Ramsey simplicity in Section 3, relating the Ramsey simplicity problem for a particular class of graphs to a packing problem. Next, we turn to random graphs, collecting some useful properties in Section 4. In Section 5 we prove Theorem1.4. The constructions of Ramsey graphs that establish
$\tilde{q}(H)$
. We then discuss general necessary and sufficient conditions for Ramsey simplicity in Section 3, relating the Ramsey simplicity problem for a particular class of graphs to a packing problem. Next, we turn to random graphs, collecting some useful properties in Section 4. In Section 5 we prove Theorem1.4. The constructions of Ramsey graphs that establish
![]() $q$
-Ramsey simplicity of
$q$
-Ramsey simplicity of
![]() $H$
are provided in Section 5.1, while the results on non-
$H$
are provided in Section 5.1, while the results on non-
![]() $q$
-Ramsey simplicity are proven in Section 5.2. The final section, Section 6, is devoted to concluding remarks and open problems.
$q$
-Ramsey simplicity are proven in Section 5.2. The final section, Section 6, is devoted to concluding remarks and open problems.
The notation used in this paper is mostly standard, except that for a graph
![]() $G$
, we write
$G$
, we write
![]() $\lambda (G)$
for the order of the largest connected component in
$\lambda (G)$
for the order of the largest connected component in
![]() $G$
. Throughout the paper, a
$G$
. Throughout the paper, a
![]() $q$
-colouring is an edge-colouring of a given graph with
$q$
-colouring is an edge-colouring of a given graph with
![]() $q$
colours and, unless otherwise specified, we will take
$q$
colours and, unless otherwise specified, we will take
![]() $[q]$
to be our colour palette. A
$[q]$
to be our colour palette. A
![]() $q$
-edge-coloured graph
$q$
-edge-coloured graph
![]() $\Gamma$
is simply a graph
$\Gamma$
is simply a graph
![]() $\Gamma$
equipped with an edge-colouring
$\Gamma$
equipped with an edge-colouring
![]() $f\,:\, E(\Gamma ) \rightarrow [q]$
. Given a graph
$f\,:\, E(\Gamma ) \rightarrow [q]$
. Given a graph
![]() $\Gamma$
with a
$\Gamma$
with a
![]() $q$
-colouring
$q$
-colouring
![]() $f$
and any colour
$f$
and any colour
![]() $i\in [q]$
, the colour-
$i\in [q]$
, the colour-
![]() $i$
subgraph
$i$
subgraph
![]() $\Gamma _i$
of
$\Gamma _i$
of
![]() $\Gamma$
is the graph
$\Gamma$
is the graph
![]() $\Gamma _i = (V(\Gamma ), f^{-1}(i))$
consisting of all edges of
$\Gamma _i = (V(\Gamma ), f^{-1}(i))$
consisting of all edges of
![]() $\Gamma$
with the colour
$\Gamma$
with the colour
![]() $i$
.
$i$
.
2. Monotonicity in
 $q$
$q$
In this section we will prove that the property of being
![]() $q$
-Ramsey simple is monotone decreasing in the number of colours; that is, we will show that if a graph is not
$q$
-Ramsey simple is monotone decreasing in the number of colours; that is, we will show that if a graph is not
![]() $q$
-Ramsey simple for some
$q$
-Ramsey simple for some
![]() $q$
, then it cannot be
$q$
, then it cannot be
![]() $q^{\prime}$
-Ramsey simple for any
$q^{\prime}$
-Ramsey simple for any
![]() $q^{\prime}\geq q$
.
$q^{\prime}\geq q$
.
Lemma 2.1.
If
![]() $H$
is not
$H$
is not
![]() $q$
-Ramsey simple, then
$q$
-Ramsey simple, then
![]() $H$
is not
$H$
is not
![]() $(q+1)$
-Ramsey simple.
$(q+1)$
-Ramsey simple.
Note that
![]() $q$
-Ramsey simplicity does not observe any monotonicity with respect to the graph
$q$
-Ramsey simplicity does not observe any monotonicity with respect to the graph
![]() $H$
. Indeed, we know that any tree on
$H$
. Indeed, we know that any tree on
![]() $t$
vertices is
$t$
vertices is
![]() $2$
-Ramsey simple [Reference Szabó, Zumstein and Zürcher20], whereas the clique
$2$
-Ramsey simple [Reference Szabó, Zumstein and Zürcher20], whereas the clique
![]() $K_t$
is not [Reference Burr, Erdős and Lovász9]. Similarly, there exist graphs that are
$K_t$
is not [Reference Burr, Erdős and Lovász9]. Similarly, there exist graphs that are
![]() $q$
-Ramsey simple but contain subgraphs that are not. For instance, Theorem 2.1.3 in [Reference Grinshpun17] shows that any 3-connected graph
$q$
-Ramsey simple but contain subgraphs that are not. For instance, Theorem 2.1.3 in [Reference Grinshpun17] shows that any 3-connected graph
![]() $H$
containing a vertex
$H$
containing a vertex
![]() $v$
of minimum degree such that
$v$
of minimum degree such that
![]() $N(v)$
is contained in an independent set of size
$N(v)$
is contained in an independent set of size
![]() $2\delta (H)-1$
is 2-Ramsey simple. Hence, while
$2\delta (H)-1$
is 2-Ramsey simple. Hence, while
![]() $K_{\delta }$
for
$K_{\delta }$
for
![]() $\delta \geq 3$
is not
$\delta \geq 3$
is not
![]() $2$
-Ramsey simple, the following supergraph of it is: add
$2$
-Ramsey simple, the following supergraph of it is: add
![]() $2\delta -1$
new vertices to
$2\delta -1$
new vertices to
![]() $K_\delta$
with a complete bipartite graph connecting them to the clique, and then add another vertex
$K_\delta$
with a complete bipartite graph connecting them to the clique, and then add another vertex
![]() $v$
connected to exactly
$v$
connected to exactly
![]() $\delta$
of the
$\delta$
of the
![]() $2\delta -1$
new vertices.
$2\delta -1$
new vertices.
Proof of Lemma
2.1. Assume
![]() $H$
is not
$H$
is not
![]() $q$
-Ramsey simple, that is,
$q$
-Ramsey simple, that is,
![]() $s_q(H) \gt q(\delta (H)-1)+1$
. Suppose for a contradiction that there exists a graph
$s_q(H) \gt q(\delta (H)-1)+1$
. Suppose for a contradiction that there exists a graph
![]() $G\in \mathcal{M}_{q+1}(H)$
such that
$G\in \mathcal{M}_{q+1}(H)$
such that
![]() $G$
contains a vertex
$G$
contains a vertex
![]() $v$
of degree
$v$
of degree
![]() $(q+1)(\delta (H)-1)+1$
. Let
$(q+1)(\delta (H)-1)+1$
. Let
![]() $e$
be an arbitrary edge incident to
$e$
be an arbitrary edge incident to
![]() $v$
.
$v$
.
By the minimality of
![]() $G$
, we know that the graph
$G$
, we know that the graph
![]() $G-e$
has an
$G-e$
has an
![]() $H$
-free
$H$
-free
![]() $(q+1)$
-colouring
$(q+1)$
-colouring
![]() $c$
. Now, if there are at most
$c$
. Now, if there are at most
![]() $\delta (H)-2$
edges that are incident to
$\delta (H)-2$
edges that are incident to
![]() $v$
and have colour
$v$
and have colour
![]() $q+1$
under
$q+1$
under
![]() $c$
, then we can give
$c$
, then we can give
![]() $e$
colour
$e$
colour
![]() $q+1$
to obtain an
$q+1$
to obtain an
![]() $H$
-free
$H$
-free
![]() $(q+1)$
-colouring of
$(q+1)$
-colouring of
![]() $G$
, contradicting
$G$
, contradicting
![]() $G \in \mathcal{M}_{q+1}(H)$
. Hence we may assume that there are at least
$G \in \mathcal{M}_{q+1}(H)$
. Hence we may assume that there are at least
![]() $\delta (H)-1$
edges incident to
$\delta (H)-1$
edges incident to
![]() $v$
that have colour
$v$
that have colour
![]() $q+1$
. Let
$q+1$
. Let
![]() $G_0$
be the subgraph of
$G_0$
be the subgraph of
![]() $G$
containing all edges that have colours in
$G$
containing all edges that have colours in
![]() $[q]$
under
$[q]$
under
![]() $c$
together with the edge
$c$
together with the edge
![]() $e$
, i.e.,
$e$
, i.e.,
![]() $G_0 = G - c^{-1}(q+1)$
. We then know that
$G_0 = G - c^{-1}(q+1)$
. We then know that
![]() $d_{G_0}(v) \leq (q+1)(\delta (H)-1)+1 - (\delta (H)-1) = q(\delta (H)-1)+1 \lt s_q(H)$
. If
$d_{G_0}(v) \leq (q+1)(\delta (H)-1)+1 - (\delta (H)-1) = q(\delta (H)-1)+1 \lt s_q(H)$
. If
![]() $G_0$
is not
$G_0$
is not
![]() $q$
-Ramsey for
$q$
-Ramsey for
![]() $H$
, then
$H$
, then
![]() $G_0$
has an
$G_0$
has an
![]() $H$
-free
$H$
-free
![]() $q$
-colouring
$q$
-colouring
![]() $c^{\prime}$
, and extending
$c^{\prime}$
, and extending
![]() $c^{\prime}$
to the graph
$c^{\prime}$
to the graph
![]() $G$
by colouring the edges in
$G$
by colouring the edges in
![]() $E(G)\setminus E(G_0)$
with colour
$E(G)\setminus E(G_0)$
with colour
![]() $q+1$
gives an
$q+1$
gives an
![]() $H$
-free
$H$
-free
![]() $(q+1)$
-colouring of
$(q+1)$
-colouring of
![]() $G$
, a contradiction. Therefore,
$G$
, a contradiction. Therefore,
![]() $G_0\rightarrow _q H$
.
$G_0\rightarrow _q H$
.
But
![]() $d_{G_0}(v) \lt s_q(H)$
, so
$d_{G_0}(v) \lt s_q(H)$
, so
![]() $G_0$
cannot be minimal
$G_0$
cannot be minimal
![]() $q$
-Ramsey for
$q$
-Ramsey for
![]() $H$
, and in particular, the vertex
$H$
, and in particular, the vertex
![]() $v$
cannot be part of a minimal
$v$
cannot be part of a minimal
![]() $q$
-Ramsey subgraph of
$q$
-Ramsey subgraph of
![]() $G_0$
. Thus
$G_0$
. Thus
![]() $G_0-v\rightarrow _q H$
. But the restriction of
$G_0-v\rightarrow _q H$
. But the restriction of
![]() $c$
to
$c$
to
![]() $G_0-v$
is
$G_0-v$
is
![]() $H$
-free by our choice of
$H$
-free by our choice of
![]() $c$
, which again leads to a contradiction.
$c$
, which again leads to a contradiction.
Hence,
![]() $H$
cannot be
$H$
cannot be
![]() $(q+1)$
-Ramsey simple.
$(q+1)$
-Ramsey simple.
3. Conditions for Ramsey simplicity
The goal of this section is to establish necessary and sufficient conditions for Ramsey simplicity, which we will later apply to the random graph to prove several parts of Theorem1.4 (and Theorem5.1). More specifically, we will relate the problem of determining whether a graph is
![]() $q$
-Ramsey simple to a certain packing problem.
$q$
-Ramsey simple to a certain packing problem.
Throughout this section we will assume that
![]() $H$
is a connected graph with a unique vertex of minimum degree, denoted by
$H$
is a connected graph with a unique vertex of minimum degree, denoted by
![]() $u$
. Further, we will write
$u$
. Further, we will write
![]() $F$
for the subgraph induced by the neighbourhood of
$F$
for the subgraph induced by the neighbourhood of
![]() $u$
in
$u$
in
![]() $H$
, that is,
$H$
, that is,
![]() $F = H[N(u)]$
. As suggested by the statement of Theorem5.1, the structure of this graph
$F = H[N(u)]$
. As suggested by the statement of Theorem5.1, the structure of this graph
![]() $F$
will play a key role in determining whether
$F$
will play a key role in determining whether
![]() $H$
is
$H$
is
![]() $q$
-Ramsey simple.
$q$
-Ramsey simple.
We begin with the necessary condition.
Proposition 3.1.
Let
![]() $q \ge 2$
, let
$q \ge 2$
, let
![]() $H$
be a connected graph containing a unique vertex
$H$
be a connected graph containing a unique vertex
![]() $u$
of minimum degree, and let
$u$
of minimum degree, and let
![]() $F = H[N(u)]$
. Suppose
$F = H[N(u)]$
. Suppose
![]() $H$
is
$H$
is
![]() $q$
-Ramsey simple. Then there exists a
$q$
-Ramsey simple. Then there exists a
![]() $q$
-edge-coloured graph
$q$
-edge-coloured graph
![]() $\Gamma$
on
$\Gamma$
on
![]() $q(\delta (H) - 1) + 1$
vertices such that for every set
$q(\delta (H) - 1) + 1$
vertices such that for every set
![]() $U \subseteq V(\Gamma )$
of
$U \subseteq V(\Gamma )$
of
![]() $\delta (H)$
vertices and for every colour
$\delta (H)$
vertices and for every colour
![]() $i \in [q]$
, there exists a copy
$i \in [q]$
, there exists a copy
![]() $F_{U,i}$
of
$F_{U,i}$
of
![]() $F$
in
$F$
in
![]() $\Gamma [U]$
whose edges are all of colour
$\Gamma [U]$
whose edges are all of colour
![]() $i$
.
$i$
.
Proof. Let
![]() $G$
be a minimal
$G$
be a minimal
![]() $q$
-Ramsey graph for
$q$
-Ramsey graph for
![]() $H$
with a vertex
$H$
with a vertex
![]() $w$
of degree
$w$
of degree
![]() $q(\delta (H) - 1) + 1$
. Let
$q(\delta (H) - 1) + 1$
. Let
![]() $\Gamma = G[N(w)]$
be the subgraph of
$\Gamma = G[N(w)]$
be the subgraph of
![]() $G$
induced by the neighbourhood of
$G$
induced by the neighbourhood of
![]() $w$
. By minimality, there is a
$w$
. By minimality, there is a
![]() $q$
-colouring
$q$
-colouring
![]() $c$
of
$c$
of
![]() $G - w$
, and in particular of
$G - w$
, and in particular of
![]() $\Gamma$
, without any monochromatic copies of
$\Gamma$
, without any monochromatic copies of
![]() $H$
.
$H$
.
Since
![]() $G$
itself is
$G$
itself is
![]() $q$
-Ramsey for
$q$
-Ramsey for
![]() $H$
, no matter how we extend the colouring
$H$
, no matter how we extend the colouring
![]() $c$
to the edges incident to
$c$
to the edges incident to
![]() $w$
, we must create a monochromatic copy of
$w$
, we must create a monochromatic copy of
![]() $H$
. Given any subset
$H$
. Given any subset
![]() $U$
of
$U$
of
![]() $\delta (H)$
vertices in
$\delta (H)$
vertices in
![]() $\Gamma$
and any colour
$\Gamma$
and any colour
![]() $i \in [q]$
, colour the edges from
$i \in [q]$
, colour the edges from
![]() $w$
to
$w$
to
![]() $U$
with colour
$U$
with colour
![]() $i$
, and colour the remaining edges incident to
$i$
, and colour the remaining edges incident to
![]() $w$
evenly with the other colours, so that each is used
$w$
evenly with the other colours, so that each is used
![]() $\delta (H) - 1$
times. Any monochromatic copy of
$\delta (H) - 1$
times. Any monochromatic copy of
![]() $H$
must involve at least
$H$
must involve at least
![]() $\delta (H)$
edges incident to
$\delta (H)$
edges incident to
![]() $w$
, and hence must be of colour
$w$
, and hence must be of colour
![]() $i$
and contain all the vertices in
$i$
and contain all the vertices in
![]() $U$
. As
$U$
. As
![]() $w$
has degree
$w$
has degree
![]() $\delta (H)$
in this monochromatic subgraph, it must play the role of
$\delta (H)$
in this monochromatic subgraph, it must play the role of
![]() $u$
in
$u$
in
![]() $H$
, and therefore we must find a colour-
$H$
, and therefore we must find a colour-
![]() $i$
copy of
$i$
copy of
![]() $F$
in
$F$
in
![]() $\Gamma [U]$
.
$\Gamma [U]$
.
As it turns out, under some additional constraints, the above necessary condition becomes sufficient. Since our aim will be to apply these conditions to a random graph, we describe several pseudorandom properties concerning the degrees, connectivity, and expansion of the target graph
![]() $H$
that will help us in the construction of minimal Ramsey graphs with vertices of low degree. These properties are collected in the definition below. As might be expected, for a large range of values of
$H$
that will help us in the construction of minimal Ramsey graphs with vertices of low degree. These properties are collected in the definition below. As might be expected, for a large range of values of
![]() $p$
, the random graph
$p$
, the random graph
![]() $G(n,p)$
is very likely to satisfy these properties.
$G(n,p)$
is very likely to satisfy these properties.
Definition 3.2 (Well-behaved). We say an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $H$
is well-behaved if it satisfies the following properties:
$H$
is well-behaved if it satisfies the following properties:
-
(W1)
 $H$
has a unique vertex
$H$
has a unique vertex
 $u$
of minimum degree
$u$
of minimum degree
 $\delta (H)$
,
$\delta (H)$
, -
(W2) every pair of vertices in
 $H$
has codegree at most
$H$
has codegree at most
 $\tfrac 12 \delta (H)$
,
$\tfrac 12 \delta (H)$
, -
(W3)
 $H$
is
$H$
is
 $3$
-connected, and
$3$
-connected, and
-
(W4) removing at most
 $\delta (H)$
vertices from
$\delta (H)$
vertices from
 $H$
cannot create a component of size
$H$
cannot create a component of size
 $k \in \left[{\tfrac 12 \delta (H), \tfrac 12 n}\right]$
.
$k \in \left[{\tfrac 12 \delta (H), \tfrac 12 n}\right]$
.
We now show that a well-behaved graph
![]() $H$
is guaranteed to be
$H$
is guaranteed to be
![]() $q$
-Ramsey simple if it admits the existence of a colour pattern as in Proposition 3.1 in which the maximum degree of each
$q$
-Ramsey simple if it admits the existence of a colour pattern as in Proposition 3.1 in which the maximum degree of each
![]() $\Gamma _i$
is not too large.
$\Gamma _i$
is not too large.
Proposition 3.3.
Let
![]() $q \ge 2$
, let
$q \ge 2$
, let
![]() $H$
be an
$H$
be an
![]() $n$
-vertex well-behaved graph, and let
$n$
-vertex well-behaved graph, and let
![]() $F = H[N(u)]$
be the subgraph induced by the neighbourhood of the unique minimum degree vertex
$F = H[N(u)]$
be the subgraph induced by the neighbourhood of the unique minimum degree vertex
![]() $u$
. Suppose there exists a
$u$
. Suppose there exists a
![]() $q$
-edge-coloured graph
$q$
-edge-coloured graph
![]() $\Gamma$
on
$\Gamma$
on
![]() $q(\delta (H) - 1) + 1$
vertices such that:
$q(\delta (H) - 1) + 1$
vertices such that:
-
(i) for every set
 $U \subseteq V(\Gamma )$
of
$U \subseteq V(\Gamma )$
of
 $\delta (H)$
vertices and for every colour
$\delta (H)$
vertices and for every colour
 $i \in [q]$
, there exists a copy
$i \in [q]$
, there exists a copy
 $F_{U,i}$
of
$F_{U,i}$
of
 $F$
in
$F$
in
 $\Gamma [U]$
whose edges are all of colour
$\Gamma [U]$
whose edges are all of colour
 $i$
, and
$i$
, and
-
(ii) for each
 $i \in [q]$
, the colour-
$i \in [q]$
, the colour-
 $i$
subgraph
$i$
subgraph
 $\Gamma _i$
of
$\Gamma _i$
of
 $\Gamma$
has maximum degree at most
$\Gamma$
has maximum degree at most
 $\delta (H) - 1$
.
$\delta (H) - 1$
.
Then
![]() $H$
is
$H$
is
![]() $q$
-Ramsey simple.
$q$
-Ramsey simple.
Propositions 3.1 and 3.3 imply that, when establishing the
![]() $q$
-Ramsey simplicity of a well-behaved graph
$q$
-Ramsey simplicity of a well-behaved graph
![]() $H$
, we can focus our attention on the neighbourhood of the minimum degree vertex. We remark that the extra conditions required in Proposition 3.3, the well-behavedness of
$H$
, we can focus our attention on the neighbourhood of the minimum degree vertex. We remark that the extra conditions required in Proposition 3.3, the well-behavedness of
![]() $H$
and property (ii), may not be necessary but they enable us to more easily maintain control over potential copies of
$H$
and property (ii), may not be necessary but they enable us to more easily maintain control over potential copies of
![]() $H$
when constructing the minimal
$H$
when constructing the minimal
![]() $q$
-Ramsey graph
$q$
-Ramsey graph
![]() $G$
.
$G$
.
Given the graph
![]() $\Gamma$
, when we build from it a
$\Gamma$
, when we build from it a
![]() $q$
-Ramsey graph
$q$
-Ramsey graph
![]() $G$
we shall, as is common practice in the field, make extensive use of signal senders, which are gadgets that allow us to prescribe colour patterns on the edges of a graph.
$G$
we shall, as is common practice in the field, make extensive use of signal senders, which are gadgets that allow us to prescribe colour patterns on the edges of a graph.
Definition 3.4 (Signal senders). Given a graph
![]() $H$
, a number of colours
$H$
, a number of colours
![]() $q \ge 2$
, a distance
$q \ge 2$
, a distance
![]() $d \ge 1$
, and two edges
$d \ge 1$
, and two edges
![]() $e$
and
$e$
and
![]() $f$
, a positive (or negative) signal sender
$f$
, a positive (or negative) signal sender
![]() $S^+(H,q,d,e,f)$
(or
$S^+(H,q,d,e,f)$
(or
![]() $S^-(H,q,d,e,f)$
) is a graph
$S^-(H,q,d,e,f)$
) is a graph
![]() $S$
that contains
$S$
that contains
![]() $e$
and
$e$
and
![]() $f$
and satisfies:
$f$
and satisfies:
-
(i)
 $S$
can be
$S$
can be
 $q$
-coloured without monochromatic copies of
$q$
-coloured without monochromatic copies of
 $H$
,
$H$
, -
(ii) in any such colouring,
 $e$
and
$e$
and
 $f$
have the same (or different) colour(s), and
$f$
have the same (or different) colour(s), and
-
(iii) the edges
 $e$
and
$e$
and
 $f$
are at distance at least
$f$
are at distance at least
 $d$
in
$d$
in
 $S$
.
$S$
.
The edges
![]() $e$
and
$e$
and
![]() $f$
are called the signal edges of
$f$
are called the signal edges of
![]() $S$
.
$S$
.
Fortunately for us, signal senders exist for all
![]() $3$
-connected graphs, as shown by Rödl and Siggers [Reference Rödl and Siggers26], building on earlier work of Burr, Erdős, and Lovász [Reference Burr, Erdős and Lovász9] and Burr, Nešetřil, and Rödl [Reference Burr, Nešetřil and Rödl27].
$3$
-connected graphs, as shown by Rödl and Siggers [Reference Rödl and Siggers26], building on earlier work of Burr, Erdős, and Lovász [Reference Burr, Erdős and Lovász9] and Burr, Nešetřil, and Rödl [Reference Burr, Nešetřil and Rödl27].
Theorem 3.5 ([Reference Rödl and Siggers26]). If
![]() $H$
is
$H$
is
![]() $3$
-connected, then for any
$3$
-connected, then for any
![]() $q \ge 2$
and
$q \ge 2$
and
![]() $d \ge 1$
, there are positive and negative signal senders
$d \ge 1$
, there are positive and negative signal senders
![]() $S^+(H,q,d,e,f)$
and
$S^+(H,q,d,e,f)$
and
![]() $S^-(H,q,d,e,f)$
.
$S^-(H,q,d,e,f)$
.
The utility of signal senders lies in the ability to force pairs of edges in an
![]() $H$
-free colouring of a graph
$H$
-free colouring of a graph
![]() $G$
to have the same (or different, in the negative case) colours. This is achieved through the process of attachment; given a graph
$G$
to have the same (or different, in the negative case) colours. This is achieved through the process of attachment; given a graph
![]() $G$
and a pair of distinct edges
$G$
and a pair of distinct edges
![]() $h_1, h_2 \in E(G)$
, we attach to
$h_1, h_2 \in E(G)$
, we attach to
![]() $G$
a signal sender
$G$
a signal sender
![]() $S^+(H,q,d,e,f)$
(or
$S^+(H,q,d,e,f)$
(or
![]() $S^-(H,q,d,e,f)$
), defined on a disjoint set of vertices, between
$S^-(H,q,d,e,f)$
), defined on a disjoint set of vertices, between
![]() $h_1$
and
$h_1$
and
![]() $h_2$
by identifying the signal edges
$h_2$
by identifying the signal edges
![]() $e$
and
$e$
and
![]() $f$
of
$f$
of
![]() $S$
with the edges
$S$
with the edges
![]() $h_1$
and
$h_1$
and
![]() $h_2$
of
$h_2$
of
![]() $G$
. In this next result, we show that attachment cannot create unexpected copies of our target graph
$G$
. In this next result, we show that attachment cannot create unexpected copies of our target graph
![]() $H$
, provided that the signal edges are sufficiently far apart.
$H$
, provided that the signal edges are sufficiently far apart.
Lemma 3.6.
Let
![]() $q\geq 2$
, let
$q\geq 2$
, let
![]() $H$
be any 3-connected graph, and let
$H$
be any 3-connected graph, and let
![]() $d \ge v(H)$
. Let
$d \ge v(H)$
. Let
![]() $S = S^+(H,q,d,e,f)$
or
$S = S^+(H,q,d,e,f)$
or
![]() $S = S^-(H,q,d,e,f)$
be a signal sender, let
$S = S^-(H,q,d,e,f)$
be a signal sender, let
![]() $G$
be any graph on a disjoint set of vertices, and let
$G$
be any graph on a disjoint set of vertices, and let
![]() $g,h \in E(G)$
induce a matching in
$g,h \in E(G)$
induce a matching in
![]() $G$
. If the graph
$G$
. If the graph
![]() $G^{\prime}$
is formed by attaching
$G^{\prime}$
is formed by attaching
![]() $S$
to
$S$
to
![]() $g$
and
$g$
and
![]() $h$
, then, for any copy
$h$
, then, for any copy
![]() $H_0$
of
$H_0$
of
![]() $H$
in
$H$
in
![]() $G^{\prime}$
, we have either
$G^{\prime}$
, we have either
![]() $H_0 \subseteq G$
or
$H_0 \subseteq G$
or
![]() $H_0 \subseteq S$
.
$H_0 \subseteq S$
.
Proof. Let
![]() $H_0$
be a copy of
$H_0$
be a copy of
![]() $H$
in
$H$
in
![]() $G'$
and suppose for the sake of contradiction that
$G'$
and suppose for the sake of contradiction that
![]() $H_0$
is neither fully contained in
$H_0$
is neither fully contained in
![]() $G$
nor in
$G$
nor in
![]() $S$
. We can then find edges
$S$
. We can then find edges
![]() $h_1 \in E(H_0) \cap \left ( E(S) \setminus E(G) \right )$
and
$h_1 \in E(H_0) \cap \left ( E(S) \setminus E(G) \right )$
and
![]() $h_2 \in E(H_0) \cap \left ( E(G) \setminus E(S) \right )$
. Since the only edges of
$h_2 \in E(H_0) \cap \left ( E(G) \setminus E(S) \right )$
. Since the only edges of
![]() $S$
spanned by
$S$
spanned by
![]() $V(G)$
are
$V(G)$
are
![]() $e$
and
$e$
and
![]() $f$
, which are identified with
$f$
, which are identified with
![]() $g,h \in E(G)$
, it follows that
$g,h \in E(G)$
, it follows that
![]() $h_1$
must contain a vertex
$h_1$
must contain a vertex
![]() $x \in V(S) \setminus V(G)$
. Similarly, since
$x \in V(S) \setminus V(G)$
. Similarly, since
![]() $g$
and
$g$
and
![]() $h$
induce a matching in
$h$
induce a matching in
![]() $G$
, they are the only edges of
$G$
, they are the only edges of
![]() $G$
spanned by
$G$
spanned by
![]() $V(S)$
, and hence
$V(S)$
, and hence
![]() $h_2$
must contain a vertex
$h_2$
must contain a vertex
![]() $y \in V(G) \setminus V(S)$
.
$y \in V(G) \setminus V(S)$
.
Now, by
![]() $3$
-connectivity,
$3$
-connectivity,
![]() $H_0$
contains three internally-vertex-disjoint paths between
$H_0$
contains three internally-vertex-disjoint paths between
![]() $x$
and
$x$
and
![]() $y$
. Since
$y$
. Since
![]() $V(S) \cap V(G) = e \cup f$
, each of these paths must pass through a distinct endpoint of one of the signal edges
$V(S) \cap V(G) = e \cup f$
, each of these paths must pass through a distinct endpoint of one of the signal edges
![]() $e$
and
$e$
and
![]() $f$
. There must be one path meeting
$f$
. There must be one path meeting
![]() $e$
and another meeting
$e$
and another meeting
![]() $f$
, and the portions of these paths that lie within the signal sender contain a path from
$f$
, and the portions of these paths that lie within the signal sender contain a path from
![]() $e$
to
$e$
to
![]() $f$
within
$f$
within
![]() $V(H_0) \cap V(S)$
. However, this contradicts
$V(H_0) \cap V(S)$
. However, this contradicts
![]() $e$
and
$e$
and
![]() $f$
being at distance
$f$
being at distance
![]() $d \ge v(H)$
.
$d \ge v(H)$
.
Armed with these preliminaries, we can now prove Proposition 3.3.
Proof of Proposition
3.3. We shall take a slightly indirect route to certifying the
![]() $q$
-Ramsey simplicity of
$q$
-Ramsey simplicity of
![]() $H$
. Rather than constructing a minimal
$H$
. Rather than constructing a minimal
![]() $q$
-Ramsey graph with minimum degree
$q$
-Ramsey graph with minimum degree
![]() $q(\delta (H) - 1)+1$
, we will instead build a graph
$q(\delta (H) - 1)+1$
, we will instead build a graph
![]() $G$
such that:
$G$
such that:
-
(a)
 $G \rightarrow _q H$
,
$G \rightarrow _q H$
, -
(b)
 $G$
has a vertex
$G$
has a vertex
 $w$
of degree
$w$
of degree
 $q(\delta (H) - 1) + 1$
, and
$q(\delta (H) - 1) + 1$
, and -
(c)
 $G - w \not \rightarrow _q H$
.
$G - w \not \rightarrow _q H$
.
Since
![]() $G$
is
$G$
is
![]() $q$
-Ramsey for
$q$
-Ramsey for
![]() $H$
, it must contain a minimal
$H$
, it must contain a minimal
![]() $q$
-Ramsey subgraph
$q$
-Ramsey subgraph
![]() $G^{\prime} \subseteq G$
. By virtue of (c), we have
$G^{\prime} \subseteq G$
. By virtue of (c), we have
![]() $w \in V(G^{\prime})$
, and hence
$w \in V(G^{\prime})$
, and hence
![]() $\delta (G^{\prime}) \le d_{G^{\prime}}(w) \le d_G(w) = q(\delta (H) - 1)+1$
. In light of the general lower bound, we must in fact have equality, and hence
$\delta (G^{\prime}) \le d_{G^{\prime}}(w) \le d_G(w) = q(\delta (H) - 1)+1$
. In light of the general lower bound, we must in fact have equality, and hence
![]() $G^{\prime}$
bears witness to the
$G^{\prime}$
bears witness to the
![]() $q$
-Ramsey simplicity of
$q$
-Ramsey simplicity of
![]() $H$
.
$H$
.

Figure 2. Construction of
![]() $G$
.
$G$
.
To construct this
![]() $q$
-Ramsey graph
$q$
-Ramsey graph
![]() $G$
, we start with the graph
$G$
, we start with the graph
![]() $\Gamma$
. Recall that, for each set
$\Gamma$
. Recall that, for each set
![]() $U$
of
$U$
of
![]() $\delta (H)$
vertices of
$\delta (H)$
vertices of
![]() $\Gamma$
and for each colour
$\Gamma$
and for each colour
![]() $i \in [q]$
, there is a colour-
$i \in [q]$
, there is a colour-
![]() $i$
copy
$i$
copy
![]() $F_{U,i}$
of
$F_{U,i}$
of
![]() $F$
in
$F$
in
![]() $\Gamma [U]$
. We will wish to complete these to potential monochromatic copies of
$\Gamma [U]$
. We will wish to complete these to potential monochromatic copies of
![]() $H$
. To this end, let
$H$
. To this end, let
![]() $R = H - \left (\{u\} \cup N(u) \right )$
be the remainder of
$R = H - \left (\{u\} \cup N(u) \right )$
be the remainder of
![]() $H$
after we remove the minimum degree vertex
$H$
after we remove the minimum degree vertex
![]() $u$
and its neighbourhood. Then, for every
$u$
and its neighbourhood. Then, for every
![]() $U$
and
$U$
and
![]() $i$
, we include a copy
$i$
, we include a copy
![]() $R_{U,i}$
of
$R_{U,i}$
of
![]() $R$
on a disjoint set of vertices, adding the necessary edges so that
$R$
on a disjoint set of vertices, adding the necessary edges so that
![]() $R_{U,i} \cup F_{U,i}$
forms a copy of
$R_{U,i} \cup F_{U,i}$
forms a copy of
![]() $H - u$
. We call the resulting graph
$H - u$
. We call the resulting graph
![]() $\Gamma ^+$
.
$\Gamma ^+$
.
Now recall that the graph
![]() $\Gamma$
comes with an edge-colouring, which we extend by colouring the edges in
$\Gamma$
comes with an edge-colouring, which we extend by colouring the edges in
![]() $R_{U,i}$
and between
$R_{U,i}$
and between
![]() $R_{U,i}$
and
$R_{U,i}$
and
![]() $F_{U,i}$
with the colour
$F_{U,i}$
with the colour
![]() $i$
. Denote by
$i$
. Denote by
![]() $c$
the resulting colouring of
$c$
the resulting colouring of
![]() $\Gamma ^+$
. To force the correct colouring, we shall use signal senders. Note that, since
$\Gamma ^+$
. To force the correct colouring, we shall use signal senders. Note that, since
![]() $H$
is well-behaved, property (W3) ensures
$H$
is well-behaved, property (W3) ensures
![]() $H$
is
$H$
is
![]() $3$
-connected, and hence by Theorem3.5 positive and negative signal senders exist.
$3$
-connected, and hence by Theorem3.5 positive and negative signal senders exist.
We introduce a matching
![]() $e_1, e_2, \ldots, e_q$
of
$e_1, e_2, \ldots, e_q$
of
![]() $q$
edges, again on a set of new vertices. For every pair
$q$
edges, again on a set of new vertices. For every pair
![]() $i \lt j$
, we attach a negative signal sender
$i \lt j$
, we attach a negative signal sender
![]() $S_{i,j} = S^-(H,q,v(H),e_i,e_j)$
between
$S_{i,j} = S^-(H,q,v(H),e_i,e_j)$
between
![]() $e_i$
and
$e_i$
and
![]() $e_j$
. As we shall see later, this will ensure that these edges all receive distinct colours in an
$e_j$
. As we shall see later, this will ensure that these edges all receive distinct colours in an
![]() $H$
-free colouring. Now, for every edge
$H$
-free colouring. Now, for every edge
![]() $f$
in
$f$
in
![]() $\Gamma ^+$
, we attach a positive signal sender
$\Gamma ^+$
, we attach a positive signal sender
![]() $S_f = S^+(H,q,v(H),e_{c(f)},f)$
between
$S_f = S^+(H,q,v(H),e_{c(f)},f)$
between
![]() $e_{c(f)}$
and
$e_{c(f)}$
and
![]() $f$
. Finally, we introduce a new vertex
$f$
. Finally, we introduce a new vertex
![]() $w$
and make it adjacent to every vertex in
$w$
and make it adjacent to every vertex in
![]() $\Gamma$
. This completes our construction of the graph
$\Gamma$
. This completes our construction of the graph
![]() $G$
, which is depicted in Figure 2.
$G$
, which is depicted in Figure 2.
Observe that
![]() $d_G(w) = v(\Gamma ) = q(\delta (H) - 1) + 1$
, and so condition (b) is already satisfied. We shall now verify conditions (a) and (c) in the following claims.
$d_G(w) = v(\Gamma ) = q(\delta (H) - 1) + 1$
, and so condition (b) is already satisfied. We shall now verify conditions (a) and (c) in the following claims.
Claim 3.7.
The graph
![]() $G$
is
$G$
is
![]() $q$
-Ramsey for
$q$
-Ramsey for
![]() $H$
.
$H$
.
Proof. Suppose for a contradiction that we have an
![]() $H$
-free
$H$
-free
![]() $q$
-colouring of
$q$
-colouring of
![]() $G$
. First observe that, by Definition 3.4(ii), if the signal sender
$G$
. First observe that, by Definition 3.4(ii), if the signal sender
![]() $S_{i,j}$
is
$S_{i,j}$
is
![]() $H$
-free, then the edges
$H$
-free, then the edges
![]() $e_i$
and
$e_i$
and
![]() $e_j$
must receive different colours. As this is true for each pair
$e_j$
must receive different colours. As this is true for each pair
![]() $i \lt j$
, we may, relabelling colours if necessary, assume that each edge
$i \lt j$
, we may, relabelling colours if necessary, assume that each edge
![]() $e_i$
receives colour
$e_i$
receives colour
![]() $i$
.
$i$
.
Next, for each edge
![]() $f$
in
$f$
in
![]() $\Gamma ^+$
, consider the signal sender
$\Gamma ^+$
, consider the signal sender
![]() $S_f$
. If this does not contain a monochromatic copy of
$S_f$
. If this does not contain a monochromatic copy of
![]() $H$
, then
$H$
, then
![]() $e_{c(f)}$
and
$e_{c(f)}$
and
![]() $f$
must have the same colour, and thus
$f$
must have the same colour, and thus
![]() $f$
receives the colour
$f$
receives the colour
![]() $c(f)$
. Hence we have forced the desired colouring on
$c(f)$
. Hence we have forced the desired colouring on
![]() $\Gamma ^+$
.
$\Gamma ^+$
.
This brings us to the vertex
![]() $w$
. Since it has degree
$w$
. Since it has degree
![]() $q(\delta (H) - 1) + 1$
, there must be some colour
$q(\delta (H) - 1) + 1$
, there must be some colour
![]() $i$
and a set
$i$
and a set
![]() $U \subseteq V(\Gamma )$
of size
$U \subseteq V(\Gamma )$
of size
![]() $\delta (H)$
such that the edges between
$\delta (H)$
such that the edges between
![]() $w$
and
$w$
and
![]() $U$
are all of colour
$U$
are all of colour
![]() $i$
. However, appealing to condition (i) of Proposition 3.3, we find a colour-
$i$
. However, appealing to condition (i) of Proposition 3.3, we find a colour-
![]() $i$
copy
$i$
copy
![]() $F_{U,i}$
of
$F_{U,i}$
of
![]() $F$
in
$F$
in
![]() $\Gamma [U]$
, which we can complete to a monochromatic copy of
$\Gamma [U]$
, which we can complete to a monochromatic copy of
![]() $H$
by attaching
$H$
by attaching
![]() $w$
and
$w$
and
![]() $R_{U,i}$
, contradicting our supposition.
$R_{U,i}$
, contradicting our supposition.
Claim 3.8.
The graph
![]() $G - w$
is not
$G - w$
is not
![]() $q$
-Ramsey for
$q$
-Ramsey for
![]() $H$
.
$H$
.
Proof. We provide an
![]() $H$
-free
$H$
-free
![]() $q$
-colouring of
$q$
-colouring of
![]() $G - w$
. To start, we give
$G - w$
. To start, we give
![]() $\Gamma ^+$
the colouring
$\Gamma ^+$
the colouring
![]() $c$
, and, for each
$c$
, and, for each
![]() $i \in [q]$
, colour the edge
$i \in [q]$
, colour the edge
![]() $e_i$
of the matching with the colour
$e_i$
of the matching with the colour
![]() $i$
. Observe that, under this colouring, the signal edges of each positive signal sender
$i$
. Observe that, under this colouring, the signal edges of each positive signal sender
![]() $S_f$
in
$S_f$
in
![]() $G$
have the same colour, while those of negative signal senders
$G$
have the same colour, while those of negative signal senders
![]() $S_{i,j}$
receive different colours. By Definition 3.4, we can find an
$S_{i,j}$
receive different colours. By Definition 3.4, we can find an
![]() $H$
-free colouring of each signal sender that agrees with the colouring of the signal edges. We use these to extend our colouring to the signal senders as well, thereby obtaining a
$H$
-free colouring of each signal sender that agrees with the colouring of the signal edges. We use these to extend our colouring to the signal senders as well, thereby obtaining a
![]() $q$
-colouring of
$q$
-colouring of
![]() $G - w$
.
$G - w$
.
Now suppose for a contradiction that this colouring gives rise to a colour-
![]() $i$
copy
$i$
copy
![]() $H_0$
of
$H_0$
of
![]() $H$
for some
$H$
for some
![]() $i \in [q]$
. First, observe that it follows from Lemma 3.6 that
$i \in [q]$
. First, observe that it follows from Lemma 3.6 that
![]() $H_0$
is fully contained either in a signal sender or in
$H_0$
is fully contained either in a signal sender or in
![]() $\Gamma ^+ \cup \{ e_i\, :\, i \in [q] \}$
. Since the signal senders were coloured without monochromatic copies of
$\Gamma ^+ \cup \{ e_i\, :\, i \in [q] \}$
. Since the signal senders were coloured without monochromatic copies of
![]() $H$
, and the edges
$H$
, and the edges
![]() $\{e_i\,:\, i \in [q]\}$
are isolated in the latter graph, we need only show that we cannot have
$\{e_i\,:\, i \in [q]\}$
are isolated in the latter graph, we need only show that we cannot have
![]() $H_0 \subseteq \Gamma ^+$
.
$H_0 \subseteq \Gamma ^+$
.
We next claim that
![]() $H_0$
can only meet at most one subgraph
$H_0$
can only meet at most one subgraph
![]() $R_{U,j}$
, for some subset
$R_{U,j}$
, for some subset
![]() $U$
and colour
$U$
and colour
![]() $j$
. First, note that since all edges incident to the vertices in
$j$
. First, note that since all edges incident to the vertices in
![]() $R_{U,j}$
are of colour
$R_{U,j}$
are of colour
![]() $j$
, and
$j$
, and
![]() $H_0$
is of colour
$H_0$
is of colour
![]() $i$
, we must have
$i$
, we must have
![]() $j = i$
. Now, suppose instead that there are two sets
$j = i$
. Now, suppose instead that there are two sets
![]() $U$
and
$U$
and
![]() $U^{\prime}$
such that
$U^{\prime}$
such that
![]() $V(H_0) \cap V(R_{U,i})$
and
$V(H_0) \cap V(R_{U,i})$
and
![]() $V(H_0) \cap V(R_{U^{\prime},i})$
are both nonempty. As the sets
$V(H_0) \cap V(R_{U^{\prime},i})$
are both nonempty. As the sets
![]() $V(R_{U,i})$
and
$V(R_{U,i})$
and
![]() $V(R_{U^{\prime},i})$
are disjoint, we may assume without loss of generality that
$V(R_{U^{\prime},i})$
are disjoint, we may assume without loss of generality that
![]() $|{V(H_0) \cap V(R_{U,i})}| \le \tfrac 12 n$
.
$|{V(H_0) \cap V(R_{U,i})}| \le \tfrac 12 n$
.
Since
![]() $R_{U,i}$
is only attached to
$R_{U,i}$
is only attached to
![]() $\Gamma$
through the vertices in
$\Gamma$
through the vertices in
![]() $U$
, the set
$U$
, the set
![]() $U$
must be a cut-set for the subgraph
$U$
must be a cut-set for the subgraph
![]() $H_0$
. Let
$H_0$
. Let
![]() $x \in V(H_0) \cap V(R_{U,i})$
be an arbitrary vertex, and let
$x \in V(H_0) \cap V(R_{U,i})$
be an arbitrary vertex, and let
![]() $K$
be the component of
$K$
be the component of
![]() $x$
in
$x$
in
![]() $H_0 - U$
. We clearly have
$H_0 - U$
. We clearly have
![]() $|{K}| \le |{V(H_0) \cap V(R_{U,i})}| \le \tfrac 12 n$
.
$|{K}| \le |{V(H_0) \cap V(R_{U,i})}| \le \tfrac 12 n$
.
On the other hand, observe that
![]() $x$
is also in the copy
$x$
is also in the copy
![]() $H_{U,i}$
of
$H_{U,i}$
of
![]() $H$
supported on
$H$
supported on
![]() $\{w\} \cup V(F_{U,i}) \cup V(R_{U,i})$
. In
$\{w\} \cup V(F_{U,i}) \cup V(R_{U,i})$
. In
![]() $H_{U,i}$
, the set
$H_{U,i}$
, the set
![]() $U$
is the neighbourhood of
$U$
is the neighbourhood of
![]() $w$
, and, since
$w$
, and, since
![]() $H$
is well-behaved, condition (W2) implies
$H$
is well-behaved, condition (W2) implies
![]() $x$
has at most
$x$
has at most
![]() $\tfrac 12 \delta (H)$
neighbours in
$\tfrac 12 \delta (H)$
neighbours in
![]() $U$
. As
$U$
. As
![]() $d_{H_0}(x) \ge \delta (H)$
, this means
$d_{H_0}(x) \ge \delta (H)$
, this means
![]() $x$
must have at least
$x$
must have at least
![]() $\tfrac 12 \delta (H)$
neighbours in
$\tfrac 12 \delta (H)$
neighbours in
![]() $H_0 - U$
. Hence, we also have
$H_0 - U$
. Hence, we also have
![]() $|{K}| \ge \tfrac 12 \delta (H)$
. However, this contradicts condition (W4), as the removal of the vertices in
$|{K}| \ge \tfrac 12 \delta (H)$
. However, this contradicts condition (W4), as the removal of the vertices in
![]() $U\cap V(H_0)$
cannot create a component in
$U\cap V(H_0)$
cannot create a component in
![]() $H_0$
of size between
$H_0$
of size between
![]() $\tfrac 12 \delta (H)$
and
$\tfrac 12 \delta (H)$
and
![]() $\tfrac 12 n$
.
$\tfrac 12 n$
.
Thus,
![]() $H_0$
meets at most one subgraph
$H_0$
meets at most one subgraph
![]() $R_{U,i}$
. Now, by property (ii) of the colouring
$R_{U,i}$
. Now, by property (ii) of the colouring
![]() $c$
of
$c$
of
![]() $\Gamma$
, we have that any vertex is incident to fewer than
$\Gamma$
, we have that any vertex is incident to fewer than
![]() $\delta (H)$
edges of colour
$\delta (H)$
edges of colour
![]() $i$
in
$i$
in
![]() $\Gamma$
. Thus, in order to be part of
$\Gamma$
. Thus, in order to be part of
![]() $H_0$
, a vertex from
$H_0$
, a vertex from
![]() $\Gamma$
must have neighbours in
$\Gamma$
must have neighbours in
![]() $R_{U,i}$
as well. However, the only such vertices are those in
$R_{U,i}$
as well. However, the only such vertices are those in
![]() $U$
, and since
$U$
, and since
![]() $|{U \cup V(R_{U,i})}| = n-1$
, this does not leave us with enough vertices for a copy of
$|{U \cup V(R_{U,i})}| = n-1$
, this does not leave us with enough vertices for a copy of
![]() $H$
.
$H$
.
Our colouring is therefore indeed
![]() $H$
-free, proving the claim.
$H$
-free, proving the claim.
This shows that the graph
![]() $G$
satisfies conditions (a), (b), and (c), completing the proof of Proposition 3.3.
$G$
satisfies conditions (a), (b), and (c), completing the proof of Proposition 3.3.
4. Properties of
 $G(n,p)$
$G(n,p)$
In this section we shall establish various properties of the random graph
![]() $G(n,p)$
needed for the proof of Theorem1.4 (and Theorem5.1) and the deduction of Corollary 1.5 (and Corollary 5.2).
$G(n,p)$
needed for the proof of Theorem1.4 (and Theorem5.1) and the deduction of Corollary 1.5 (and Corollary 5.2).
4.1.
Facts about
 $G(n,p)$
$G(n,p)$
We start by describing some properties of
![]() $G(n,p)$
for different values of
$G(n,p)$
for different values of
![]() $p$
. As most of the results presented in this section are well known, we will be very brief in the proofs. We start with some bounds on the degrees and edge distribution in the random graph, for which we require the following well-known concentration bounds due to Chernoff (see [Reference McDiarmid28, Theorem 2.3] and [Reference Frieze and Karoński29, Theorem 23.6]).
$p$
. As most of the results presented in this section are well known, we will be very brief in the proofs. We start with some bounds on the degrees and edge distribution in the random graph, for which we require the following well-known concentration bounds due to Chernoff (see [Reference McDiarmid28, Theorem 2.3] and [Reference Frieze and Karoński29, Theorem 23.6]).
Lemma 4.1.
Let
![]() $X \sim Bin(n,p)$
and
$X \sim Bin(n,p)$
and
![]() $\mu = \mathbb{E}[X]$
.
$\mu = \mathbb{E}[X]$
.
-
(a) If
 $0\lt \varepsilon \lt 1$
, then
$0\lt \varepsilon \lt 1$
, then
 $\mathbb{P}(X\geq (1+\varepsilon )\mu )\leq \exp\!{\left(\frac{-\mu \varepsilon ^2}{3}\right)}$
and
$\mathbb{P}(X\geq (1+\varepsilon )\mu )\leq \exp\!{\left(\frac{-\mu \varepsilon ^2}{3}\right)}$
and
 $\mathbb{P}(X\leq (1-\varepsilon )\mu )\leq \exp\!{\left(\frac{-\mu \varepsilon ^2}{2}\right)}$
.
$\mathbb{P}(X\leq (1-\varepsilon )\mu )\leq \exp\!{\left(\frac{-\mu \varepsilon ^2}{2}\right)}$
. -
(b) For all
 $t \geq 7\mu$
, we have
$t \geq 7\mu$
, we have
 $\mathbb{P}(X \geq t) \leq \exp\!({-}t)$
.
$\mathbb{P}(X \geq t) \leq \exp\!({-}t)$
.
The following two lemmas collect some folklore bounds on the degrees and number of edges in
![]() $G(n,p)$
. We start by controlling the degrees.
$G(n,p)$
. We start by controlling the degrees.
Lemma 4.2 (Degrees in
![]() $G(n,p)$
). Let
$G(n,p)$
). Let
![]() $p=p(n)\in (0,1)$
, and let
$p=p(n)\in (0,1)$
, and let
![]() $H\sim G(n,p)$
. Then a.a.s. the following bounds on the maximum degree hold:
$H\sim G(n,p)$
. Then a.a.s. the following bounds on the maximum degree hold:
-
(a) for any fixed integer
 $k \ge 2$
, we have
$k \ge 2$
, we have
 $\Delta (H)\geq k-1$
when
$\Delta (H)\geq k-1$
when
 $p\gg n^{-\frac{k}{k-1}}$
, and
$p\gg n^{-\frac{k}{k-1}}$
, and
-
(b) for any
 $f = f(n)$
satisfying
$f = f(n)$
satisfying
 $1 \ll f = n^{o(1)}$
, we have
$1 \ll f = n^{o(1)}$
, we have
 $\Delta (H) \geq \frac{\log n}{\log\!(f \log n)}$
when
$\Delta (H) \geq \frac{\log n}{\log\!(f \log n)}$
when
 $p = \frac{1}{nf}$
.
$p = \frac{1}{nf}$
.
Moreover, if
![]() $p\gg \frac{\log n}{n}$
, then with probability at least
$p\gg \frac{\log n}{n}$
, then with probability at least
![]() $1-n^{-2}$
we have
$1-n^{-2}$
we have
-
(c)
 $d_H(v)=(1\pm o(1))np$
for every
$d_H(v)=(1\pm o(1))np$
for every
 $v\in V(H)$
.
$v\in V(H)$
.
Proof. If
![]() $p\gg n^{-\frac{k}{k-1}}$
for any integer
$p\gg n^{-\frac{k}{k-1}}$
for any integer
![]() $k\geq 2$
, then
$k\geq 2$
, then
![]() $H$
a.a.s. contains a star with
$H$
a.a.s. contains a star with
![]() $k-1$
edges, and hence
$k-1$
edges, and hence
![]() $\Delta (H) \ge k-1$
; see Theorem5.3 in [Reference Frieze and Karoński29] for more details. If
$\Delta (H) \ge k-1$
; see Theorem5.3 in [Reference Frieze and Karoński29] for more details. If
![]() $p = \frac{1}{nf}$
, a straightforward calculation shows that the expected number of vertices of degree at least
$p = \frac{1}{nf}$
, a straightforward calculation shows that the expected number of vertices of degree at least
![]() $\frac{\log n}{\log\!(f \log n)}$
tends to infinity, which combined with an application of the second moment method (or of Theorem 3.1(ii) in [Reference Bollobás30]) establishes the desired result. Part (c) follows by applying Lemma 4.1(a) to the degree of each vertex, and then taking a union bound over all
$\frac{\log n}{\log\!(f \log n)}$
tends to infinity, which combined with an application of the second moment method (or of Theorem 3.1(ii) in [Reference Bollobás30]) establishes the desired result. Part (c) follows by applying Lemma 4.1(a) to the degree of each vertex, and then taking a union bound over all
![]() $n$
vertices.
$n$
vertices.
We can also bound the number of edges, both globally and, provided the edge probability is not too low, in all large induced subgraphs. Both parts follow from simple applications of Lemma 4.1(a), in the second case in combination with a union bound, so we omit the proof.
Lemma 4.3 (Edge counts in
![]() $G(n,p)$
). Let
$G(n,p)$
). Let
![]() $p=p(n)\in (0,1)$
with
$p=p(n)\in (0,1)$
with
![]() $p\gg n^{-2}$
, and let
$p\gg n^{-2}$
, and let
![]() $H\sim G(n,p)$
. Then a.a.s. the following statements hold:
$H\sim G(n,p)$
. Then a.a.s. the following statements hold:
-
(a)
 $e(H)=(1\pm o(1))\frac{n^2p}{2}$
, and
$e(H)=(1\pm o(1))\frac{n^2p}{2}$
, and
-
(b) if
 $p \gg \frac{\log n}{n}$
, then with probability at least
$p \gg \frac{\log n}{n}$
, then with probability at least
 $1 - n^{-2}$
, every set
$1 - n^{-2}$
, every set
 $S \subseteq V(H)$
of size
$S \subseteq V(H)$
of size
 $s \ge \frac{20 \log n}{p}$
satisfies
$s \ge \frac{20 \log n}{p}$
satisfies
 $e_H(S)\geq \frac{1}{4}s^2p$
.
$e_H(S)\geq \frac{1}{4}s^2p$
.
Aside from knowing how many edges the random graph contains, we shall also need some knowledge about how they are distributed. The following result describes the structure of sparse random graphs.
Lemma 4.4.
Let
![]() $p=p(n)\in (0,1)$
with
$p=p(n)\in (0,1)$
with
![]() $p\ll n^{-1}$
, and let
$p\ll n^{-1}$
, and let
![]() $H\sim G(n,p)$
. Then a.a.s.
$H\sim G(n,p)$
. Then a.a.s.
![]() $H$
is a forest, and moreover the order
$H$
is a forest, and moreover the order
![]() $\lambda (H)$
of its largest component satisfies the following bounds:
$\lambda (H)$
of its largest component satisfies the following bounds:
-
(a)
 $\lambda (H) \le \log n$
,
$\lambda (H) \le \log n$
, -
(b) if
 $p\ll n^{-\frac{k+1}{k}}$
for some constant
$p\ll n^{-\frac{k+1}{k}}$
for some constant
 $k \in \mathbb{N}$
, then
$k \in \mathbb{N}$
, then
 $\lambda (H) \le k$
, and
$\lambda (H) \le k$
, and
-
(c) if
 $p = \frac{1}{nf}$
for some
$p = \frac{1}{nf}$
for some
 $f = f(n)$
satisfying
$f = f(n)$
satisfying
 $1 \ll f = n^{o(1)}$
, then
$1 \ll f = n^{o(1)}$
, then
 $\lambda (H) \le (1 + o(1)) \frac{\log n}{\log f}$
.
$\lambda (H) \le (1 + o(1)) \frac{\log n}{\log f}$
.
Proof. That
![]() $H$
contains no cycles, and hence is a forest, can be shown by taking a union bound over all possible cycles; see Theorem 2.1 in [Reference Frieze and Karoński29] for the details. Now suppose
$H$
contains no cycles, and hence is a forest, can be shown by taking a union bound over all possible cycles; see Theorem 2.1 in [Reference Frieze and Karoński29] for the details. Now suppose
![]() $H$
were to contain a tree on
$H$
were to contain a tree on
![]() $t$
vertices. There are
$t$
vertices. There are
![]() $\binom{n}{t}$
choices for the vertex set of the tree and
$\binom{n}{t}$
choices for the vertex set of the tree and
![]() $t^{t-2}$
possible labelled trees on that set, each of which appears with probability
$t^{t-2}$
possible labelled trees on that set, each of which appears with probability
![]() $p^{t-1}$
. Thus, the probability that
$p^{t-1}$
. Thus, the probability that
![]() $H$
contains any
$H$
contains any
![]() $t$
-vertex tree is at most
$t$
-vertex tree is at most
![]() $\binom{n}{t}t^{t-2}p^{t-1}$
. It is then straightforward to verify that, in each of the above cases, plugging in the claimed bound on
$\binom{n}{t}t^{t-2}p^{t-1}$
. It is then straightforward to verify that, in each of the above cases, plugging in the claimed bound on
![]() $\lambda (H)$
for
$\lambda (H)$
for
![]() $t$
makes the corresponding probability
$t$
makes the corresponding probability
![]() $o(1)$
.
$o(1)$
.
Switching to a much denser range, we find that when the edge probability is sufficiently large, not only does
![]() $G(n,p)$
contain cycles, but every edge is contained in a triangle. The proof is an easy application of the union bound and is thus omitted.
$G(n,p)$
contain cycles, but every edge is contained in a triangle. The proof is an easy application of the union bound and is thus omitted.
Lemma 4.5.
Let
![]() $p = p(n)\in (0,1)$
be such that
$p = p(n)\in (0,1)$
be such that
![]() $p \gg \sqrt{\frac{\log n}{n} }$
, and let
$p \gg \sqrt{\frac{\log n}{n} }$
, and let
![]() $H\sim G(n,p)$
. Then a.a.s. every edge of
$H\sim G(n,p)$
. Then a.a.s. every edge of
![]() $H$
is contained in a triangle.
$H$
is contained in a triangle.
Finally, as might be expected, random graphs are highly likely to be well-behaved (recall Definition 3.2). This intuition is confirmed by the following lemma; we include a brief sketch of the proof.
Lemma 4.6.
If
![]() $\frac{\log n}{n} \ll p \ll 1$
, then a.a.s.
$\frac{\log n}{n} \ll p \ll 1$
, then a.a.s.
![]() $H \sim G(n,p)$
is well-behaved.
$H \sim G(n,p)$
is well-behaved.
Proof. Properties (W1) and (W3) are established in Theorem 3.9(i) of [Reference Bollobás30] and Theorem 4.3 in [Reference Frieze and Karoński29], respectively. Moreover, by Lemma 4.2(c) we may condition on
![]() $\delta (H)=(1\pm o(1))np$
. For property 2, observe that the distribution of the codegree of a given pair of vertices is
$\delta (H)=(1\pm o(1))np$
. For property 2, observe that the distribution of the codegree of a given pair of vertices is
![]() $\mathrm{Bin}(n-2,p^2)$
. Now, considering the two cases
$\mathrm{Bin}(n-2,p^2)$
. Now, considering the two cases
![]() $p^2 \geq \frac{10 \log n}{n}$
and
$p^2 \geq \frac{10 \log n}{n}$
and
![]() $p^2 \leq \frac{10 \log n}{n}$
separately and applying parts (a) and (b) of Lemma 4.1 respectively yields the required result. Finally, for property (W4), note that for any fixed integers
$p^2 \leq \frac{10 \log n}{n}$
separately and applying parts (a) and (b) of Lemma 4.1 respectively yields the required result. Finally, for property (W4), note that for any fixed integers
![]() $1\leq s\leq \delta (H)$
and
$1\leq s\leq \delta (H)$
and
![]() $k \in \left[{\tfrac 12 \delta (H), \tfrac 12 n}\right]$
and sets
$k \in \left[{\tfrac 12 \delta (H), \tfrac 12 n}\right]$
and sets
![]() $U\in \binom{V(H)}{s}$
and
$U\in \binom{V(H)}{s}$
and
![]() $K\in \binom{V(H)-U}{k}$
, the probability that removing
$K\in \binom{V(H)-U}{k}$
, the probability that removing
![]() $U$
from
$U$
from
![]() $H$
leaves
$H$
leaves
![]() $K$
isolated is precisely
$K$
isolated is precisely
![]() $(1-p)^{k(n-k-s)}$
. Now taking a union bound over all choices of
$(1-p)^{k(n-k-s)}$
. Now taking a union bound over all choices of
![]() $s,k,U,$
and
$s,k,U,$
and
![]() $K$
shows that the probability that property (W4) fails is
$K$
shows that the probability that property (W4) fails is
![]() $o(1)$
.
$o(1)$
.
4.2. Transference lemma
As we will we see in the statement of Theorem5.1, our bounds on the simplicity threshold of
![]() $H \sim G(n,p)$
depend on the subgraph induced by the neighbourhood of the minimum degree vertex (which, by virtue of Lemma 4.6 and property (W1), we may assume to be unique for
$H \sim G(n,p)$
depend on the subgraph induced by the neighbourhood of the minimum degree vertex (which, by virtue of Lemma 4.6 and property (W1), we may assume to be unique for
![]() $p \gg \frac{\log n}{n}$
). Our next lemma allows us to transfer what we know about the random graph
$p \gg \frac{\log n}{n}$
). Our next lemma allows us to transfer what we know about the random graph
![]() $G(\delta (H), p)$
to this subgraph.
$G(\delta (H), p)$
to this subgraph.
Lemma 4.7.
Let
![]() $p=p(n)\in (0,1)$
be such that
$p=p(n)\in (0,1)$
be such that
![]() $\frac{\log n}{n} \ll p \ll 1$
. For every
$\frac{\log n}{n} \ll p \ll 1$
. For every
![]() $s\in [0.5np,2np]$
, let
$s\in [0.5np,2np]$
, let
![]() $\mathcal{P}_s$
be a graph property, and assume that a random graph
$\mathcal{P}_s$
be a graph property, and assume that a random graph
![]() $G_s\sim G(s,p)$
satisfies
$G_s\sim G(s,p)$
satisfies
Then
![]() $H\sim G(n,p)$
a.a.s. has a unique minimum degree vertex
$H\sim G(n,p)$
a.a.s. has a unique minimum degree vertex
![]() $u$
and
$u$
and
![]() $H[N(u)]\in \mathcal{P}_{d_H(u)}$
.
$H[N(u)]\in \mathcal{P}_{d_H(u)}$
.
Proof. We will follow an approach similar to that used in the proof of Corollary 2.1.4 in [Reference Grinshpun17]. Before we proceed with the proof, we introduce some notation and facts that we will need later on. Let us first fix some
![]() $\beta _n=o(1)$
such that
$\beta _n=o(1)$
such that
for every
![]() $s\in [0.5np,2np]$
. Moreover, let
$s\in [0.5np,2np]$
. Moreover, let
![]() $X_\delta$
denote the event that
$X_\delta$
denote the event that
![]() $H$
has a unique vertex of minimum degree and
$H$
has a unique vertex of minimum degree and
![]() $0.5np\leq \delta (H) \leq 2np$
. By Lemma 4.6, specifically property (W1), and Lemma 4.2 we know that
$0.5np\leq \delta (H) \leq 2np$
. By Lemma 4.6, specifically property (W1), and Lemma 4.2 we know that
![]() $X_\delta$
holds with high probability. In particular, we can find
$X_\delta$
holds with high probability. In particular, we can find
![]() $\delta _n=o(1)$
such that
$\delta _n=o(1)$
such that
We will also use the following two facts:
-
(1) There exists
 $\gamma _n= o(1)$
such that, for any
$\gamma _n= o(1)$
such that, for any
 $d\geq 0$
, we have
$d\geq 0$
, we have
 ${\mathbb{P}}[\delta (H) = d] \leq \gamma _n$
.
${\mathbb{P}}[\delta (H) = d] \leq \gamma _n$
. -
(2) For any
 $d\geq 0$
, if
$d\geq 0$
, if
 $H^{\prime}\sim G(n-1,p)$
, we have
$H^{\prime}\sim G(n-1,p)$
, we have
 ${\mathbb{P}}[\delta (H^{\prime}) \geq d-1] \geq{\mathbb{P}}[\delta (H) \geq d]$
.
${\mathbb{P}}[\delta (H^{\prime}) \geq d-1] \geq{\mathbb{P}}[\delta (H) \geq d]$
.
Part (1) follows from the proof of Theorem 3.9(i) in [Reference Bollobás30]. Part (2) follows from the fact that removing a vertex from a graph can reduce the minimum degree by at most one and that we can sample a graph
![]() $H\sim G(n,p)$
by first sampling
$H\sim G(n,p)$
by first sampling
![]() $H^{\prime}\sim G(n-1,p)$
and then adding each potential edge containing the last vertex with probability
$H^{\prime}\sim G(n-1,p)$
and then adding each potential edge containing the last vertex with probability
![]() $p$
, independently of all previous choices.
$p$
, independently of all previous choices.
Next, let
![]() $\varepsilon _n=o(1)$
be chosen such that
$\varepsilon _n=o(1)$
be chosen such that
![]() $\varepsilon _n=\omega (\!\max \{\beta _n,\gamma _n,\delta _n\}).$
We further let
$\varepsilon _n=\omega (\!\max \{\beta _n,\gamma _n,\delta _n\}).$
We further let
![]() $t_n$
be the smallest integer such that
$t_n$
be the smallest integer such that
![]() ${\mathbb{P}} (\delta (H) \leq t_n) \geq 1-\varepsilon _n$
. Note that, by the minimality of
${\mathbb{P}} (\delta (H) \leq t_n) \geq 1-\varepsilon _n$
. Note that, by the minimality of
![]() $t_n$
, we then have
$t_n$
, we then have
![]() ${\mathbb{P}} (\delta (H) \leq t_n-1) \lt 1-\varepsilon _n$
. Using (1) for
${\mathbb{P}} (\delta (H) \leq t_n-1) \lt 1-\varepsilon _n$
. Using (1) for
![]() $d = t_n$
, we conclude
$d = t_n$
, we conclude
Moreover, since
![]() $\varepsilon _n\gt \gamma _n + \delta _n$
, we obtain
$\varepsilon _n\gt \gamma _n + \delta _n$
, we obtain
![]() ${\mathbb{P}} (\delta (H) \leq t_n) \lt 1-\delta _n \lt{\mathbb{P}} (\delta (H) \leq 2np)$
and thus
${\mathbb{P}} (\delta (H) \leq t_n) \lt 1-\delta _n \lt{\mathbb{P}} (\delta (H) \leq 2np)$
and thus
![]() $t_n\leq 2np$
.
$t_n\leq 2np$
.
Since
![]() $H \sim G(n,p)$
, the subgraph
$H \sim G(n,p)$
, the subgraph
![]() $H - v$
, for any fixed vertex
$H - v$
, for any fixed vertex
![]() $v$
, has the distribution
$v$
, has the distribution
![]() $G\left(n-1,p\right)$
. In the following we will condition on the event
$G\left(n-1,p\right)$
. In the following we will condition on the event
![]() $X_\delta$
, and whenever we do so, we will always let
$X_\delta$
, and whenever we do so, we will always let
![]() $u$
denote the unique minimum degree vertex in
$u$
denote the unique minimum degree vertex in
![]() $H$
and write
$H$
and write
![]() $d = d_H(u)$
. We will be interested in the subgraph
$d = d_H(u)$
. We will be interested in the subgraph
![]() $H^{\prime} = H - u$
, and first need to determine how conditioning on
$H^{\prime} = H - u$
, and first need to determine how conditioning on
![]() $X_{\delta }$
affects its distribution.
$X_{\delta }$
affects its distribution.
Suppose
![]() $S \subseteq V(H^{\prime})$
is the neighbourhood of
$S \subseteq V(H^{\prime})$
is the neighbourhood of
![]() $u$
. As
$u$
. As
![]() $u$
is the only vertex of degree at most
$u$
is the only vertex of degree at most
![]() $d$
in
$d$
in
![]() $H$
, we must have
$H$
, we must have
![]() $d_{H^{\prime}}(v) \ge d+1$
for all
$d_{H^{\prime}}(v) \ge d+1$
for all
![]() $v \in V(H^{\prime}) \setminus S$
, and
$v \in V(H^{\prime}) \setminus S$
, and
![]() $d_{H^{\prime}}(v) \ge d$
for all
$d_{H^{\prime}}(v) \ge d$
for all
![]() $v \in S$
; let
$v \in S$
; let
![]() $C_S$
be the event that these lower bounds on the degrees in
$C_S$
be the event that these lower bounds on the degrees in
![]() $H^{\prime}$
hold. Aside from
$H^{\prime}$
hold. Aside from
![]() $C_S$
, however,
$C_S$
, however,
![]() $X_{\delta }$
yields no further information about the graph
$X_{\delta }$
yields no further information about the graph
![]() $H^{\prime}$
, as the edges in
$H^{\prime}$
, as the edges in
![]() $G(n,p)$
are independent. Thus, we have
$G(n,p)$
are independent. Thus, we have
Now, by the Law of Total Probability,
 \begin{align} &{\mathbb{P}}_{G(n,p)}(H[N(u)]\in \mathcal{P}_{d_H(u)} |X_{\delta }) \nonumber \\ &= \sum _{0 \le d \le n-1} \sum _{S \in \left({V\left(H^{\prime}\right) \atop d}\right)} {\mathbb{P}}_{G(n,p)} ({H[S] \in \mathcal{P}_d | X_{\delta } \land \{N(u) = S\} }) \cdot{\mathbb{P}}_{G(n,p)} ({N(u) = S | X_{\delta } }) \nonumber \\ & \geq \sum _{0.5np \le d \le t_n} \sum _{S \in \left({V\left(H^{\prime}\right) \atop d}\right)}{\mathbb{P}}_{G(n-1,p)}(H^{\prime}[S]\in \mathcal{P}_d| C_S) \cdot{\mathbb{P}}_{G(n,p)}(N(u) = S | X_{\delta }). \end{align}
\begin{align} &{\mathbb{P}}_{G(n,p)}(H[N(u)]\in \mathcal{P}_{d_H(u)} |X_{\delta }) \nonumber \\ &= \sum _{0 \le d \le n-1} \sum _{S \in \left({V\left(H^{\prime}\right) \atop d}\right)} {\mathbb{P}}_{G(n,p)} ({H[S] \in \mathcal{P}_d | X_{\delta } \land \{N(u) = S\} }) \cdot{\mathbb{P}}_{G(n,p)} ({N(u) = S | X_{\delta } }) \nonumber \\ & \geq \sum _{0.5np \le d \le t_n} \sum _{S \in \left({V\left(H^{\prime}\right) \atop d}\right)}{\mathbb{P}}_{G(n-1,p)}(H^{\prime}[S]\in \mathcal{P}_d| C_S) \cdot{\mathbb{P}}_{G(n,p)}(N(u) = S | X_{\delta }). \end{align}
Now let
![]() $d\in [0.5np, t_n]$
and
$d\in [0.5np, t_n]$
and
![]() $S\in \binom{V(H^{\prime})}{d}$
be fixed. To estimate the first factor, we observe that
$S\in \binom{V(H^{\prime})}{d}$
be fixed. To estimate the first factor, we observe that
where the second inequality follows from (2), for the third inequality we use
![]() $d\leq t_n$
, the fourth inequality follows from (1), and the last inequality comes from (4.2) and since
$d\leq t_n$
, the fourth inequality follows from (1), and the last inequality comes from (4.2) and since
![]() $\varepsilon _n=\omega (\gamma _n)$
. Hence we have
$\varepsilon _n=\omega (\gamma _n)$
. Hence we have
 \begin{align*}{\mathbb{P}}_{G(n-1,p)}({ H^{\prime}[S] \in \mathcal{P}_d | C_S }) & = 1 -{\mathbb{P}}_{G(n-1,p)}\left (H^{\prime}[S]\notin \mathcal{P}_d|C_S \right ) \\ &= 1 - \frac{{\mathbb{P}}_{G(n-1,p)}\left ( \{H^{\prime}[S]\notin \mathcal{P}_d\} \wedge C_S\right )}{{\mathbb{P}}_{G(n-1,p)}(C_S)} \\ & \geq 1 - \frac{{\mathbb{P}}_{G(n-1,p)}\left (H^{\prime}[S]\notin \mathcal{P}_d\right )}{{\mathbb{P}}_{G(n-1,p)}(C_S)} \\ & \geq 1 - \frac{{\mathbb{P}}_{G(d,p)} \left (G_d\notin \mathcal{P}_d\right )}{\varepsilon _n/2} = 1 - o(1), \end{align*}
\begin{align*}{\mathbb{P}}_{G(n-1,p)}({ H^{\prime}[S] \in \mathcal{P}_d | C_S }) & = 1 -{\mathbb{P}}_{G(n-1,p)}\left (H^{\prime}[S]\notin \mathcal{P}_d|C_S \right ) \\ &= 1 - \frac{{\mathbb{P}}_{G(n-1,p)}\left ( \{H^{\prime}[S]\notin \mathcal{P}_d\} \wedge C_S\right )}{{\mathbb{P}}_{G(n-1,p)}(C_S)} \\ & \geq 1 - \frac{{\mathbb{P}}_{G(n-1,p)}\left (H^{\prime}[S]\notin \mathcal{P}_d\right )}{{\mathbb{P}}_{G(n-1,p)}(C_S)} \\ & \geq 1 - \frac{{\mathbb{P}}_{G(d,p)} \left (G_d\notin \mathcal{P}_d\right )}{\varepsilon _n/2} = 1 - o(1), \end{align*}
where for the second inequality we use (4.5) and that
![]() $H^{\prime}[S]\sim G(d,p)$
and the final estimate uses (4.1) and
$H^{\prime}[S]\sim G(d,p)$
and the final estimate uses (4.1) and
![]() $\beta _n=o(\varepsilon _n)$
. Putting this into (4.4), we conclude that
$\beta _n=o(\varepsilon _n)$
. Putting this into (4.4), we conclude that
 \begin{align*}{\mathbb{P}}_{G(n,p)}(H[N(u)]\in \mathcal{P}_{d_H(u)} |X_{\delta }) & \geq \sum _{0.5np \le d \le t_n} \sum _{S \in \left({V(H^{\prime}) \atop d}\right)} (1-o(1)){\mathbb{P}}_{G(n,p)}(N(u) = S | X_{\delta }) \\ & = (1-o(1)){\mathbb{P}}_{G(n,p)}\left (0.5np\leq \delta (H) \leq t_n | X_{\delta } \right ) \\ & = (1-o(1)) \frac{{\mathbb{P}}_{G(n,p)}(\{\delta (H) \leq t_n\} \land X_{\delta })}{{\mathbb{P}}(X_\delta )} \\ & \geq (1-o(1)) \frac{1 -{\mathbb{P}}_{G(n,p)}(\delta (H) \gt t_n) -{\mathbb{P}}_{G(n,p)}(\overline{X_{\delta }})}{{\mathbb{P}}(X_\delta )} \\ & \geq (1-o(1)) \frac{1-\varepsilon _n-\delta _n}{1-\delta _n} = 1-o(1). \end{align*}
\begin{align*}{\mathbb{P}}_{G(n,p)}(H[N(u)]\in \mathcal{P}_{d_H(u)} |X_{\delta }) & \geq \sum _{0.5np \le d \le t_n} \sum _{S \in \left({V(H^{\prime}) \atop d}\right)} (1-o(1)){\mathbb{P}}_{G(n,p)}(N(u) = S | X_{\delta }) \\ & = (1-o(1)){\mathbb{P}}_{G(n,p)}\left (0.5np\leq \delta (H) \leq t_n | X_{\delta } \right ) \\ & = (1-o(1)) \frac{{\mathbb{P}}_{G(n,p)}(\{\delta (H) \leq t_n\} \land X_{\delta })}{{\mathbb{P}}(X_\delta )} \\ & \geq (1-o(1)) \frac{1 -{\mathbb{P}}_{G(n,p)}(\delta (H) \gt t_n) -{\mathbb{P}}_{G(n,p)}(\overline{X_{\delta }})}{{\mathbb{P}}(X_\delta )} \\ & \geq (1-o(1)) \frac{1-\varepsilon _n-\delta _n}{1-\delta _n} = 1-o(1). \end{align*}
This proves the lemma.
4.3. The smallest neighbourhood
We can now combine the results from Section 4.1 with Lemma 4.7 to obtain a sequence of corollaries describing the subgraph
![]() $F$
induced by the neighbourhood of the minimum degree vertex, which we shall later apply when proving Theorem1.4 (and Theorem5.1). As the proofs of the results in this section follow from simple applications of Lemma 4.7 combined with the corresponding results from Section 4.1, we choose to omit them.
$F$
induced by the neighbourhood of the minimum degree vertex, which we shall later apply when proving Theorem1.4 (and Theorem5.1). As the proofs of the results in this section follow from simple applications of Lemma 4.7 combined with the corresponding results from Section 4.1, we choose to omit them.
To start with, for the proof of the Ramsey simplicity of
![]() $H$
in case (a) of Theorem1.4, when
$H$
in case (a) of Theorem1.4, when
![]() $\frac{\log n}{n} \ll p\ll n^{-\frac{2}{3}}$
, it will be important that
$\frac{\log n}{n} \ll p\ll n^{-\frac{2}{3}}$
, it will be important that
![]() $F$
is an empty graph. This is guaranteed by the following corollary.
$F$
is an empty graph. This is guaranteed by the following corollary.
Corollary 4.8.
Let
![]() $p=p(n)\in (0,1)$
be such that
$p=p(n)\in (0,1)$
be such that
![]() $\frac{\log n}{n} \ll p\ll n^{-\frac{2}{3}}$
, and let
$\frac{\log n}{n} \ll p\ll n^{-\frac{2}{3}}$
, and let
![]() $H\sim G(n,p)$
. Then a.a.s.
$H\sim G(n,p)$
. Then a.a.s.
![]() $H$
has a unique minimum degree vertex
$H$
has a unique minimum degree vertex
![]() $u$
, and
$u$
, and
![]() $e(N(u))=0$
.
$e(N(u))=0$
.
For larger values of
![]() $p$
, we can control the number of edges appearing in
$p$
, we can control the number of edges appearing in
![]() $F$
, which we will require for the proofs of both simplicity and non-simplicity.
$F$
, which we will require for the proofs of both simplicity and non-simplicity.
Corollary 4.9.
Let
![]() $p=p(n)\in (0,1)$
be such that
$p=p(n)\in (0,1)$
be such that
![]() $n^{-\frac{2}{3}} \ll p\ll 1$
, and let
$n^{-\frac{2}{3}} \ll p\ll 1$
, and let
![]() $H\sim G(n,p)$
. Then a.a.s.
$H\sim G(n,p)$
. Then a.a.s.
![]() $H$
has a unique minimum degree vertex
$H$
has a unique minimum degree vertex
![]() $u$
, and the graph
$u$
, and the graph
![]() $F=H[N(u)]$
satisfies
$F=H[N(u)]$
satisfies
![]() $\frac{1}{16}n^2p^3 \leq e(F)\leq 4n^2p^3$
.
$\frac{1}{16}n^2p^3 \leq e(F)\leq 4n^2p^3$
.
Finally, in the range
![]() $n^{-\frac 23} \ll p \ll n^{-\frac 12}$
, when determining the
$n^{-\frac 23} \ll p \ll n^{-\frac 12}$
, when determining the
![]() $q$
-Ramsey simplicity of
$q$
-Ramsey simplicity of
![]() $H$
, we will make use of the fact that
$H$
, we will make use of the fact that
![]() $F$
is typically a forest with small components, while also appealing to the fact that its maximum degree cannot be too small.
$F$
is typically a forest with small components, while also appealing to the fact that its maximum degree cannot be too small.
Corollary 4.10.
Let
![]() $p=p(n)\in (0,1)$
be such that
$p=p(n)\in (0,1)$
be such that
![]() $n^{-\frac{2}{3}} \ll p\ll n^{-\frac{1}{2}}$
, and let
$n^{-\frac{2}{3}} \ll p\ll n^{-\frac{1}{2}}$
, and let
![]() $H\sim G(n,p)$
. Then a.a.s.
$H\sim G(n,p)$
. Then a.a.s.
![]() $H$
has a unique minimum degree vertex
$H$
has a unique minimum degree vertex
![]() $u$
, the graph
$u$
, the graph
![]() $F=H[N(u)]$
induces a forest, and the order
$F=H[N(u)]$
induces a forest, and the order
![]() $\lambda (F)$
of the largest component in
$\lambda (F)$
of the largest component in
![]() $F$
satisfies the following bounds:
$F$
satisfies the following bounds:
-
(a)
 $\lambda (F) \le \frac 12 \log n$
,
$\lambda (F) \le \frac 12 \log n$
, -
(b) if
 $p\ll n^{-\frac{k+1}{2k+1}}$
for some fixed integer
$p\ll n^{-\frac{k+1}{2k+1}}$
for some fixed integer
 $k \ge 2$
, then
$k \ge 2$
, then
 $\lambda (F) \le k$
, and
$\lambda (F) \le k$
, and
-
(c) if
 $p = n^{-\frac 12}f^{-1}$
for some
$p = n^{-\frac 12}f^{-1}$
for some
 $f = f(n)$
satisfying
$f = f(n)$
satisfying
 $1 \ll f = n^{o(1)}$
, then
$1 \ll f = n^{o(1)}$
, then
 $\lambda (F) \le \left (\frac 14 + o(1) \right ) \frac{\log n}{\log f}$
.
$\lambda (F) \le \left (\frac 14 + o(1) \right ) \frac{\log n}{\log f}$
.
Moreover, the maximum degree
![]() $\Delta (F)$
of
$\Delta (F)$
of
![]() $F$
a.a.s. satisfies the following:
$F$
a.a.s. satisfies the following:
-
(d) if
 $p \gg n^{-\frac{k}{2k-1}}$
for some fixed integer
$p \gg n^{-\frac{k}{2k-1}}$
for some fixed integer
 $k \ge 2$
, then
$k \ge 2$
, then
 $\Delta (F) \ge k-1$
, and
$\Delta (F) \ge k-1$
, and
-
(e) if
 $p = n^{-1/2}f^{-1}$
for some
$p = n^{-1/2}f^{-1}$
for some
 $1 \ll f = f(n) = n^{o(1)}$
, then
$1 \ll f = f(n) = n^{o(1)}$
, then
 $\Delta (F) \ge \left({\frac 12 - o(1)}\right) \frac{\log n}{\log\!( f^2 \log n )}$
.
$\Delta (F) \ge \left({\frac 12 - o(1)}\right) \frac{\log n}{\log\!( f^2 \log n )}$
.
5. Proof of Theorem1.4 and Corollary 1.5
In this section we prove Theorem1.4 and Corollary 1.5 by showing the following more precise result.
Theorem 5.1.
Let
![]() $p = p(n) \in (0,1)$
and
$p = p(n) \in (0,1)$
and
![]() $H\sim G(n,p)$
. If
$H\sim G(n,p)$
. If
![]() $\frac{\log n}{n} \ll p \ll 1$
, then
$\frac{\log n}{n} \ll p \ll 1$
, then
![]() $H$
almost surely contains a unique vertex
$H$
almost surely contains a unique vertex
![]() $u$
of minimum degree; in this case, we define
$u$
of minimum degree; in this case, we define
![]() $F = H[N(u)]$
to be the subgraph of
$F = H[N(u)]$
to be the subgraph of
![]() $H$
induced by the neighbourhood of
$H$
induced by the neighbourhood of
![]() $u$
, and denote by
$u$
, and denote by
![]() $\lambda (F)$
the order of the largest connected component in
$\lambda (F)$
the order of the largest connected component in
![]() $F$
. Then a.a.s. the following bounds hold:
$F$
. Then a.a.s. the following bounds hold:
-
(a)
 $\tilde{q}(H)=\infty$
if
$\tilde{q}(H)=\infty$
if
 $0\lt p\ll n^{-1}$
.
$0\lt p\ll n^{-1}$
. -
(b)
 $\tilde{q}(H)=\infty$
if
$\tilde{q}(H)=\infty$
if
 $\frac{\log n}{n}\ll p \ll n^{-\frac{2}{3}}$
.
$\frac{\log n}{n}\ll p \ll n^{-\frac{2}{3}}$
. -
(c)
 $\tilde{q}(H) \ge (1 + o(1)) \max \left \{ \frac{\delta (H)}{\lambda (F)^2}, \frac{\delta (H)}{80 \log n} \right \}$
if
$\tilde{q}(H) \ge (1 + o(1)) \max \left \{ \frac{\delta (H)}{\lambda (F)^2}, \frac{\delta (H)}{80 \log n} \right \}$
if
 $n^{-\frac 23} \ll p \ll n^{-\frac 12}$
.
$n^{-\frac 23} \ll p \ll n^{-\frac 12}$
. -
(d)
 $\tilde{q}(H) \leq \min \left \{\frac{\delta (H)}{\Delta (F)} + 1, \frac{\delta (H)^2}{2 e(F)} \right\}$
if
$\tilde{q}(H) \leq \min \left \{\frac{\delta (H)}{\Delta (F)} + 1, \frac{\delta (H)^2}{2 e(F)} \right\}$
if
 $n^{-\frac 23} \ll p \ll 1$
.
$n^{-\frac 23} \ll p \ll 1$
. -
(e)
 $\tilde{q}(H)=1$
if
$\tilde{q}(H)=1$
if
 $\left (\frac{\log n}{n}\right )^{1/2}\ll p \lt 1$
.
$\left (\frac{\log n}{n}\right )^{1/2}\ll p \lt 1$
.
Note that parts (a) and (b) of this theorem yield Theorem1.4(a), and together with part (c) they are proven in Section 5.1. Part (e) of this theorem is the same as Theorem1.4(c), and together with part 4 it is proven in Section 5.2. Lastly, Theorem1.4(b) follows from Lemma 2.1 and the bounds in parts (c) and (d) of the above theorem.
Additionally, by taking parts (c) and (d) of Theorem5.1 and plugging in the bounds on
![]() $\delta (H)$
,
$\delta (H)$
,
![]() $e(F)$
,
$e(F)$
,
![]() $\lambda (F)$
and
$\lambda (F)$
and
![]() $\Delta (F)$
obtained in Lemma 4.2 and Section 4.3, we can easily deduce the following quantitative result, which includes the statement of Corollary 1.5. We omit the details of these calculations.
$\Delta (F)$
obtained in Lemma 4.2 and Section 4.3, we can easily deduce the following quantitative result, which includes the statement of Corollary 1.5. We omit the details of these calculations.
Corollary 5.2.
Let
![]() $k \ge 2$
be a fixed integer and let
$k \ge 2$
be a fixed integer and let
![]() $f = f(n)$
satisfy
$f = f(n)$
satisfy
![]() $1 \ll f = n^{o(1)}$
. Let
$1 \ll f = n^{o(1)}$
. Let
![]() $p = p(n)$
satisfy
$p = p(n)$
satisfy
![]() $n^{-\frac 23} \ll p \ll \left ( \frac{\log n}{n} \right )^{\frac 12}$
and let
$n^{-\frac 23} \ll p \ll \left ( \frac{\log n}{n} \right )^{\frac 12}$
and let
![]() $H \sim G(n,p)$
. Then a.a.s. the following bounds hold:
$H \sim G(n,p)$
. Then a.a.s. the following bounds hold:
-
(a) if
 $n^{-\frac{k}{2k-1}}\ll p \ll n^{-\frac{k+1}{2k+1}}$
, then
$n^{-\frac{k}{2k-1}}\ll p \ll n^{-\frac{k+1}{2k+1}}$
, then
 $(1+o(1)) \frac{np}{k^2} \le \tilde{q}(H) \le (1+o(1))\frac{np}{k-1}$
.
$(1+o(1)) \frac{np}{k^2} \le \tilde{q}(H) \le (1+o(1))\frac{np}{k-1}$
. -
(b) if
 $p = \Theta \left({ n^{-\frac{k+1}{2k+1}} }\right)$
, then
$p = \Theta \left({ n^{-\frac{k+1}{2k+1}} }\right)$
, then
 $(1 + o(1)) \frac{np}{(k+1)^2} \le \tilde{q}(H) \le (1 + o(1))\frac{np}{k-1}.$
$(1 + o(1)) \frac{np}{(k+1)^2} \le \tilde{q}(H) \le (1 + o(1))\frac{np}{k-1}.$
-
(c) if
 $p = n^{-\frac 12} f^{-1}$
, then
$p = n^{-\frac 12} f^{-1}$
, then
 $(1+ o(1))\frac{np}{\log n} \max \left \{\frac{16 \log ^2 f}{\log n}, \frac{1}{80} \right\} \le \tilde{q}(H) \le (2+ o(1)) \frac{np \log\!( f^2 \log n)}{\log n}$
.
$(1+ o(1))\frac{np}{\log n} \max \left \{\frac{16 \log ^2 f}{\log n}, \frac{1}{80} \right\} \le \tilde{q}(H) \le (2+ o(1)) \frac{np \log\!( f^2 \log n)}{\log n}$
. -
(d) if
 $n^{-\frac 12} \ll p \ll \left ( \frac{\log n}{n} \right )^{\frac 12}$
, then
$n^{-\frac 12} \ll p \ll \left ( \frac{\log n}{n} \right )^{\frac 12}$
, then
 $1 \le \tilde{q}(H) \le \frac{8}{p}$
.
$1 \le \tilde{q}(H) \le \frac{8}{p}$
.
5.1.
Simplicity for
 $G(n,p)$
$G(n,p)$
In this section we prove the lower bounds on
![]() $\tilde{q}(G(n,p))$
from Theorem5.1. These are the positive results, showing that with high probability
$\tilde{q}(G(n,p))$
from Theorem5.1. These are the positive results, showing that with high probability
![]() $H \sim G(n,p)$
is
$H \sim G(n,p)$
is
![]() $q$
-Ramsey simple for the appropriate values of
$q$
-Ramsey simple for the appropriate values of
![]() $q$
.
$q$
.
To begin, we observe that we have nothing new to prove in case (a). By Lemma 4.4 we know
![]() $H$
is a forest with high probability when
$H$
is a forest with high probability when
![]() $p \ll n^{-1}$
. Szabó, Zumstein, and Zürcher [Reference Szabó, Zumstein and Zürcher20] proved that all forests are
$p \ll n^{-1}$
. Szabó, Zumstein, and Zürcher [Reference Szabó, Zumstein and Zürcher20] proved that all forests are
![]() $2$
-Ramsey simple, and their proof extends directly to show
$2$
-Ramsey simple, and their proof extends directly to show
![]() $q$
-Ramsey simplicity for all
$q$
-Ramsey simplicity for all
![]() $q \ge 3$
as well. For completeness, we provide the argument in Appendix A.
$q \ge 3$
as well. For completeness, we provide the argument in Appendix A.
For the remaining cases, we will show that
![]() $H$
is typically such that one can construct a minimal
$H$
is typically such that one can construct a minimal
![]() $q$
-Ramsey graph
$q$
-Ramsey graph
![]() $G$
for
$G$
for
![]() $H$
with
$H$
with
![]() $\delta (G) = q(\delta (H) - 1) + 1$
, provided, in case (c), that
$\delta (G) = q(\delta (H) - 1) + 1$
, provided, in case (c), that
![]() $q$
is not too large. By Lemma 4.6, we know that when
$q$
is not too large. By Lemma 4.6, we know that when
![]() $\frac{\log n}{n} \ll p \ll 1$
, the random graph
$\frac{\log n}{n} \ll p \ll 1$
, the random graph
![]() $H \sim G(n,p)$
is well-behaved with high probability, and hence we are in a position to apply Proposition 3.3. Thus, to prove the required results it is sufficient to show that a coloured graph
$H \sim G(n,p)$
is well-behaved with high probability, and hence we are in a position to apply Proposition 3.3. Thus, to prove the required results it is sufficient to show that a coloured graph
![]() $\Gamma$
satisfying conditions (i) and (ii) almost surely exists. We shall therefore use the results of Section 4 to describe the subgraph
$\Gamma$
satisfying conditions (i) and (ii) almost surely exists. We shall therefore use the results of Section 4 to describe the subgraph
![]() $F$
induced by the minimum degree vertex in
$F$
induced by the minimum degree vertex in
![]() $H$
. This subgraph evolves as the edge probability
$H$
. This subgraph evolves as the edge probability
![]() $p$
increases, and in each range we will construct an appropriate coloured graph
$p$
increases, and in each range we will construct an appropriate coloured graph
![]() $\Gamma$
that satisfies the conditions of the proposition.
$\Gamma$
that satisfies the conditions of the proposition.
We start with the sparse range, where
![]() $p \ll n^{-\frac 23}$
.
$p \ll n^{-\frac 23}$
.
Proof of Theorem
5.1(b). Let
![]() $q \ge 2$
, let
$q \ge 2$
, let
![]() $p$
satisfy
$p$
satisfy
![]() $\frac{\log n}{n} \ll p \ll n^{-\frac 23}$
, and let
$\frac{\log n}{n} \ll p \ll n^{-\frac 23}$
, and let
![]() $H \sim G(n,p)$
. By Lemma 4.6 and Corollary 4.8, we have with high probability that
$H \sim G(n,p)$
. By Lemma 4.6 and Corollary 4.8, we have with high probability that
![]() $H$
is well-behaved and the subgraph
$H$
is well-behaved and the subgraph
![]() $F = H[N(u)]$
induced by the neighbourhood of the minimum degree vertex
$F = H[N(u)]$
induced by the neighbourhood of the minimum degree vertex
![]() $u$
is empty. In this case, we can simply take
$u$
is empty. In this case, we can simply take
![]() $\Gamma$
to be an empty graph on
$\Gamma$
to be an empty graph on
![]() $q(\delta (H) - 1) + 1$
vertices. Properties (i) and (ii) of Proposition 3.3 are then trivially satisfied, and so it follows that
$q(\delta (H) - 1) + 1$
vertices. Properties (i) and (ii) of Proposition 3.3 are then trivially satisfied, and so it follows that
![]() $H$
is
$H$
is
![]() $q$
-Ramsey simple.
$q$
-Ramsey simple.
When
![]() $p \gg n^{-\frac 23}$
, we will begin to see edges in the neighbourhood of the minimum degree vertex. Provided
$p \gg n^{-\frac 23}$
, we will begin to see edges in the neighbourhood of the minimum degree vertex. Provided
![]() $p \ll n^{-\frac 12}$
, though, the neighbourhood remains simple in structure, and we can get reasonably sharp bounds on the number of colours for which the random graph is Ramsey simple.
$p \ll n^{-\frac 12}$
, though, the neighbourhood remains simple in structure, and we can get reasonably sharp bounds on the number of colours for which the random graph is Ramsey simple.
Proof of Theorem
5.1(c), first bound. Let
![]() $n^{-2/3}\ll p\ll n^{-1/2}$
and
$n^{-2/3}\ll p\ll n^{-1/2}$
and
![]() $H \sim G(n,p)$
. By Lemma 4.6, we know that with high probability
$H \sim G(n,p)$
. By Lemma 4.6, we know that with high probability
![]() $H$
is well-behaved. Given any
$H$
is well-behaved. Given any
![]() $\varepsilon \gt 0$
, we shall show that, as
$\varepsilon \gt 0$
, we shall show that, as
![]() $n$
tends to infinity,
$n$
tends to infinity,
![]() $H$
is with high probability
$H$
is with high probability
![]() $q$
-Ramsey simple for every
$q$
-Ramsey simple for every
![]() $q \le ({1 - 5 \varepsilon }) \frac{\delta (H)}{\lambda (F)^2}$
.
$q \le ({1 - 5 \varepsilon }) \frac{\delta (H)}{\lambda (F)^2}$
.
Corollaries 4.9 and 4.10 show that
![]() $F = H[N(u)]$
, the subgraph induced by the neighbourhood of the minimum degree vertex
$F = H[N(u)]$
, the subgraph induced by the neighbourhood of the minimum degree vertex
![]() $u$
, is with high probability a very sparse forest. More precisely, if we denote by
$u$
, is with high probability a very sparse forest. More precisely, if we denote by
![]() $T_1, T_2, \ldots, T_t$
the components of
$T_1, T_2, \ldots, T_t$
the components of
![]() $F$
that contain at least one edge, then each
$F$
that contain at least one edge, then each
![]() $T_j$
is a tree spanning at most
$T_j$
is a tree spanning at most
![]() $\lambda (F)$
vertices, and
$\lambda (F)$
vertices, and
![]() $\sum _j v(T_j) \le \varepsilon \delta (H)$
.
$\sum _j v(T_j) \le \varepsilon \delta (H)$
.
To prove simplicity, we provide a geometric construction of an edge-coloured graph
![]() $\Gamma$
on
$\Gamma$
on
![]() $q(\delta (H) - 1)+1$
vertices. Let
$q(\delta (H) - 1)+1$
vertices. Let
![]() $s$
be the largest prime number that is at most
$s$
be the largest prime number that is at most
![]() $({1 - \varepsilon }) \frac{\delta (H)}{\lambda (F)}$
. By the upper bound of Baker, Harman, and Pintz [Reference Baker, Harman and Pintz31] on prime gaps, we have
$({1 - \varepsilon }) \frac{\delta (H)}{\lambda (F)}$
. By the upper bound of Baker, Harman, and Pintz [Reference Baker, Harman and Pintz31] on prime gaps, we have
![]() $s \ge ({1 - 2 \varepsilon }) \frac{\delta (H)}{\lambda (F)}$
. Now consider the finite affine plane
$s \ge ({1 - 2 \varepsilon }) \frac{\delta (H)}{\lambda (F)}$
. Now consider the finite affine plane
![]() $\mathbb{F}_s^2$
, which has
$\mathbb{F}_s^2$
, which has
![]() $s^2$
points. Each line in the plane consists of
$s^2$
points. Each line in the plane consists of
![]() $s$
points, and the set of lines can be partitioned into
$s$
points, and the set of lines can be partitioned into
![]() $s+1$
parallel classes
$s+1$
parallel classes
![]() $C_1, C_2, \ldots, C_{s+1}$
of
$C_1, C_2, \ldots, C_{s+1}$
of
![]() $s$
lines each.
$s$
lines each.
To form the graph
![]() $\Gamma$
, we take as vertices an arbitrary set of
$\Gamma$
, we take as vertices an arbitrary set of
![]() $q(\delta (H) - 1) + 1$
points from
$q(\delta (H) - 1) + 1$
points from
![]() $\mathbb{F}_s^2$
. Note that our choices of
$\mathbb{F}_s^2$
. Note that our choices of
![]() $q$
and
$q$
and
![]() $s$
ensure that
$s$
ensure that
![]() $q(\delta (H) - 1) + 1 \le s^2$
and
$q(\delta (H) - 1) + 1 \le s^2$
and
![]() $q \leq s \le \delta (H)$
. Then, given
$q \leq s \le \delta (H)$
. Then, given
![]() $x, y \in V(\Gamma )$
, we add the edge
$x, y \in V(\Gamma )$
, we add the edge
![]() $\{x,y\}$
if and only if the line they span lies in one of the first
$\{x,y\}$
if and only if the line they span lies in one of the first
![]() $q$
parallel classes. We colour the edges by the parallel classes; that is, if the corresponding line lies in
$q$
parallel classes. We colour the edges by the parallel classes; that is, if the corresponding line lies in
![]() $C_i$
, for some
$C_i$
, for some
![]() $i \in [q]$
, we give the edge
$i \in [q]$
, we give the edge
![]() $\{x,y\}$
the colour
$\{x,y\}$
the colour
![]() $i$
.
$i$
.
We shall now show that
![]() $\Gamma$
satisfies properties (i) and (ii) of Proposition 3.3, which will show that
$\Gamma$
satisfies properties (i) and (ii) of Proposition 3.3, which will show that
![]() $H$
is
$H$
is
![]() $q$
-Ramsey simple. We start with the latter property. The colour-
$q$
-Ramsey simple. We start with the latter property. The colour-
![]() $i$
subgraph
$i$
subgraph
![]() $\Gamma _i$
of
$\Gamma _i$
of
![]() $\Gamma$
consists of pairs of points in lines in the parallel class
$\Gamma$
consists of pairs of points in lines in the parallel class
![]() $C_i$
. Each such line gives rise to a clique in
$C_i$
. Each such line gives rise to a clique in
![]() $\Gamma$
, and since the lines are parallel, these cliques are vertex-disjoint. Finally, since each line has at most
$\Gamma$
, and since the lines are parallel, these cliques are vertex-disjoint. Finally, since each line has at most
![]() $s$
points in
$s$
points in
![]() $\Gamma$
, it follows that
$\Gamma$
, it follows that
![]() $\Delta (\Gamma _i) \le s-1 \le \delta (H) - 1$
, and hence property (ii) holds.
$\Delta (\Gamma _i) \le s-1 \le \delta (H) - 1$
, and hence property (ii) holds.
For property (i), we need to show that, for any
![]() $\delta (H)$
-set
$\delta (H)$
-set
![]() $U \subseteq V(\Gamma )$
and any colour
$U \subseteq V(\Gamma )$
and any colour
![]() $i \in [q]$
, we can find a copy of
$i \in [q]$
, we can find a copy of
![]() $F$
in
$F$
in
![]() $\Gamma _i[U]$
. We shall embed the trees
$\Gamma _i[U]$
. We shall embed the trees
![]() $T_j$
one at a time. Suppose, for some
$T_j$
one at a time. Suppose, for some
![]() $j \ge 1$
, we have already embedded
$j \ge 1$
, we have already embedded
![]() $T_1, T_2, \ldots, T_{j-1}$
, and let
$T_1, T_2, \ldots, T_{j-1}$
, and let
![]() $U^{\prime} \subseteq U$
be the set of vertices we have not yet used. Since
$U^{\prime} \subseteq U$
be the set of vertices we have not yet used. Since
![]() $F$
has at most
$F$
has at most
![]() $\varepsilon \delta (H)$
non-isolated vertices, it follows that
$\varepsilon \delta (H)$
non-isolated vertices, it follows that
![]() $|{U^{\prime}}| \ge ({1 - \varepsilon }) \delta (H)$
.
$|{U^{\prime}}| \ge ({1 - \varepsilon }) \delta (H)$
.
As observed when showing property (ii), the colour-
![]() $i$
subgraph
$i$
subgraph
![]() $\Gamma _i$
is a disjoint union of at most
$\Gamma _i$
is a disjoint union of at most
![]() $s$
cliques. Hence, by the pigeonhole principle,
$s$
cliques. Hence, by the pigeonhole principle,
![]() $U^{\prime}$
meets one of these cliques in at least
$U^{\prime}$
meets one of these cliques in at least
![]() $\frac{|{U^{\prime}}|}{s}$
vertices. By our choice of
$\frac{|{U^{\prime}}|}{s}$
vertices. By our choice of
![]() $s$
, this is at least
$s$
, this is at least
![]() $\lambda (F)$
, and so
$\lambda (F)$
, and so
![]() $\Gamma _i[U^{\prime}]$
contains a clique on
$\Gamma _i[U^{\prime}]$
contains a clique on
![]() $\lambda (F)$
vertices, in which we can freely embed
$\lambda (F)$
vertices, in which we can freely embed
![]() $T_j$
.
$T_j$
.
Repeating this process, we can embed all the trees, thereby obtaining a copy of
![]() $F$
in
$F$
in
![]() $\Gamma _i[U]$
. Hence property (i) is satisfied as well, and thus
$\Gamma _i[U]$
. Hence property (i) is satisfied as well, and thus
![]() $H$
is indeed
$H$
is indeed
![]() $q$
-Ramsey simple.
$q$
-Ramsey simple.
The above construction allows us to obtain lower bounds on
![]() $\tilde{q}(H)$
whenever
$\tilde{q}(H)$
whenever
![]() $n^{-2/3}\ll p\ll n^{-1/2}$
. However, when
$n^{-2/3}\ll p\ll n^{-1/2}$
. However, when
![]() $p = n^{-\frac 12 - o(1)}$
and
$p = n^{-\frac 12 - o(1)}$
and
![]() $\lambda (F)$
gets larger, a probabilistic construction yields a better bound.
$\lambda (F)$
gets larger, a probabilistic construction yields a better bound.
Proof of Theorem
5.1(c), second bound. Let
![]() $p \ll n^{-\frac 12}$
, and let
$p \ll n^{-\frac 12}$
, and let
![]() $H \sim G(n,p)$
. Our goal is to show that if
$H \sim G(n,p)$
. Our goal is to show that if
![]() $q \le \frac{\delta (H)}{80 \log n}$
, then with high probability
$q \le \frac{\delta (H)}{80 \log n}$
, then with high probability
![]() $H$
is
$H$
is
![]() $q$
-Ramsey simple. We again start by collecting some information about the random graph
$q$
-Ramsey simple. We again start by collecting some information about the random graph
![]() $H$
, before constructing an appropriate graph
$H$
, before constructing an appropriate graph
![]() $\Gamma$
for Proposition 3.3.
$\Gamma$
for Proposition 3.3.
By Lemma 4.2(c) and Lemma 4.6, we may assume that
![]() $H$
is well-behaved with
$H$
is well-behaved with
![]() $\delta (H) = (1\pm o(1)) np$
. Furthermore, applying Corollaries 4.9 and 4.10, we know that with high probability, the subgraph
$\delta (H) = (1\pm o(1)) np$
. Furthermore, applying Corollaries 4.9 and 4.10, we know that with high probability, the subgraph
![]() $F = H[N(u)]$
induced by the neighbourhood of the minimum degree vertex is a forest with
$F = H[N(u)]$
induced by the neighbourhood of the minimum degree vertex is a forest with
![]() $o({\delta (H)})$
edges, and whose largest tree has at most
$o({\delta (H)})$
edges, and whose largest tree has at most
![]() $\log n$
vertices. We label the nontrivial components of
$\log n$
vertices. We label the nontrivial components of
![]() $F$
as
$F$
as
![]() $T_1, T_2, \ldots, T_t$
.
$T_1, T_2, \ldots, T_t$
.
We now define the
![]() $q$
-coloured graph
$q$
-coloured graph
![]() $\Gamma$
on
$\Gamma$
on
![]() $N = q(\delta (H) - 1)+1$
vertices. We take
$N = q(\delta (H) - 1)+1$
vertices. We take
![]() $\Gamma \sim G\left(N,\tfrac{1}{2}\right)$
to be a random graph with edge probability
$\Gamma \sim G\left(N,\tfrac{1}{2}\right)$
to be a random graph with edge probability
![]() $\tfrac{1}{2}$
. Once we have sampled the graph, we also equip it with a random colouring, colouring each edge independently and uniformly at random from the
$\tfrac{1}{2}$
. Once we have sampled the graph, we also equip it with a random colouring, colouring each edge independently and uniformly at random from the
![]() $q$
colours.
$q$
colours.
Observe that for each colour
![]() $i \in [q]$
, the colour-
$i \in [q]$
, the colour-
![]() $i$
subgraph
$i$
subgraph
![]() $\Gamma _i \subseteq \Gamma$
has the distribution
$\Gamma _i \subseteq \Gamma$
has the distribution
![]() $G\left(N,\tfrac{1}{2q}\right)$
. Hence, it follows from Lemma 4.2(c), combined with a union bound over the number of colours
$G\left(N,\tfrac{1}{2q}\right)$
. Hence, it follows from Lemma 4.2(c), combined with a union bound over the number of colours
![]() $q$
, that with high probability
$q$
, that with high probability
![]() $\Delta (\Gamma _i) \le ({1 + o(1)}) \tfrac{N}{2q} \lt \delta (H)$
for every
$\Delta (\Gamma _i) \le ({1 + o(1)}) \tfrac{N}{2q} \lt \delta (H)$
for every
![]() $i\in [q]$
. This establishes property (ii) of Proposition 3.3.
$i\in [q]$
. This establishes property (ii) of Proposition 3.3.
We now need to show that property (i) also holds with high probability. That is, we need to ensure that, for every colour
![]() $i \in [q]$
and every set
$i \in [q]$
and every set
![]() $U \subseteq V(\Gamma )$
of
$U \subseteq V(\Gamma )$
of
![]() $\delta (H)$
vertices, we can find a copy of
$\delta (H)$
vertices, we can find a copy of
![]() $F$
in
$F$
in
![]() $\Gamma _i[U]$
. We shall once again do this by proving the stronger fact that, taking
$\Gamma _i[U]$
. We shall once again do this by proving the stronger fact that, taking
![]() $\varepsilon \ge 0$
, for any set
$\varepsilon \ge 0$
, for any set
![]() $U^{\prime}$
of
$U^{\prime}$
of
![]() $(1- \varepsilon ) \delta (H) \ge \tfrac 12 np$
vertices, and any tree
$(1- \varepsilon ) \delta (H) \ge \tfrac 12 np$
vertices, and any tree
![]() $T$
on at most
$T$
on at most
![]() $\log n$
vertices, we can embed a copy of
$\log n$
vertices, we can embed a copy of
![]() $T$
in
$T$
in
![]() $\Gamma _i[U^{\prime}]$
. We can then greedily embed the components of
$\Gamma _i[U^{\prime}]$
. We can then greedily embed the components of
![]() $F$
one at a time; as
$F$
one at a time; as
![]() $F$
only has
$F$
only has
![]() $o(\delta (H))$
edges, we will always have at least
$o(\delta (H))$
edges, we will always have at least
![]() $(1- \varepsilon ) \delta (H)$
vertices remaining when embedding one of its components.
$(1- \varepsilon ) \delta (H)$
vertices remaining when embedding one of its components.
Applying Lemma 4.3(b) combined with a union bound over the colours
![]() $i \in [q]$
, we know that with high probability the monochromatic subgraphs
$i \in [q]$
, we know that with high probability the monochromatic subgraphs
![]() $\Gamma _i$
have the property that the number of edges spanned by any set of
$\Gamma _i$
have the property that the number of edges spanned by any set of
![]() $\tfrac 12 np \gt \frac{20 \log N}{1/(2q)}$
vertices is at least
$\tfrac 12 np \gt \frac{20 \log N}{1/(2q)}$
vertices is at least
![]() $\tfrac 14 \left({\tfrac 12 np}\right)^2 \tfrac{1}{2q} \gt 2 np \log n$
.
$\tfrac 14 \left({\tfrac 12 np}\right)^2 \tfrac{1}{2q} \gt 2 np \log n$
.
Since the set
![]() $U^{\prime}$
spans at least
$U^{\prime}$
spans at least
![]() $2 np \log n$
edges, the average degree in any such subgraph is at least
$2 np \log n$
edges, the average degree in any such subgraph is at least
![]() $2 \log n$
. By repeatedly removing low-degree vertices, we obtain a subgraph with minimum degree at least
$2 \log n$
. By repeatedly removing low-degree vertices, we obtain a subgraph with minimum degree at least
![]() $\log n$
. It is then trivial to embed a tree on at most
$\log n$
. It is then trivial to embed a tree on at most
![]() $\log n$
vertices in this subgraph, as at each vertex, we will always have enough unused neighbours to embed its children. Thus, we can find disjoint copies of the trees
$\log n$
vertices in this subgraph, as at each vertex, we will always have enough unused neighbours to embed its children. Thus, we can find disjoint copies of the trees
![]() $T_1, T_2, \ldots, T_t$
, thereby constructing a copy of
$T_1, T_2, \ldots, T_t$
, thereby constructing a copy of
![]() $F$
in
$F$
in
![]() $\Gamma _i[U]$
. This proves property (i), and so by Proposition 3.3 it follows that
$\Gamma _i[U]$
. This proves property (i), and so by Proposition 3.3 it follows that
![]() $H$
is
$H$
is
![]() $q$
-Ramsey simple.
$q$
-Ramsey simple.
5.2.
Non-simplicity for
 $G(n,p)$
$G(n,p)$
In this section we prove the upper bounds on
![]() $\tilde{q}(H)$
from Theorem5.1. These are the negative results, showing that with high probability
$\tilde{q}(H)$
from Theorem5.1. These are the negative results, showing that with high probability
![]() $H \sim G(n,p)$
is not
$H \sim G(n,p)$
is not
![]() $q$
-Ramsey simple for large values of
$q$
-Ramsey simple for large values of
![]() $q$
.
$q$
.
We begin with the upper bounds for case (d) of our theorem. For this, we shall make use of the necessary condition provided by Proposition 3.1. In the proof below, we first establish that, if the neighbourhood of the minimum degree vertex exhibits a high maximum degree, then
![]() $H$
cannot be
$H$
cannot be
![]() $q$
-Ramsey simple for a large enough
$q$
-Ramsey simple for a large enough
![]() $q$
. For this, we will need the following result from [Reference Kogan32].
$q$
. For this, we will need the following result from [Reference Kogan32].
Theorem 5.3 ([Reference Kogan32]). Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex graph of average degree
$n$
-vertex graph of average degree
![]() $d$
and let
$d$
and let
![]() $k \in \mathbb{N}$
. Then there is a set
$k \in \mathbb{N}$
. Then there is a set
![]() $U$
of at least
$U$
of at least
![]() $(k+1)n/(d+k+1)$
vertices such that
$(k+1)n/(d+k+1)$
vertices such that
![]() $\Delta (G[U]) \le k$
.
$\Delta (G[U]) \le k$
.
Proof of Theorem
5.1(d). Let
![]() $n^{-2/3}\ll p\ll 1$
and
$n^{-2/3}\ll p\ll 1$
and
![]() $H\sim G(n,p)$
. By Lemma 4.6, we know that
$H\sim G(n,p)$
. By Lemma 4.6, we know that
![]() $H$
has a unique vertex
$H$
has a unique vertex
![]() $u$
of minimum degree. As before, we set
$u$
of minimum degree. As before, we set
![]() $F = H[N(u)]$
. Suppose that
$F = H[N(u)]$
. Suppose that
![]() $H$
is
$H$
is
![]() $q$
-Ramsey simple; it follows from Proposition 3.1 that there is an edge-coloured graph
$q$
-Ramsey simple; it follows from Proposition 3.1 that there is an edge-coloured graph
![]() $\Gamma$
on
$\Gamma$
on
![]() $N = q(\delta - 1)+1$
vertices such that the induced graph on every
$N = q(\delta - 1)+1$
vertices such that the induced graph on every
![]() $\delta (H)$
-subset of the vertices of
$\delta (H)$
-subset of the vertices of
![]() $\Gamma$
contains, in each colour, a copy of
$\Gamma$
contains, in each colour, a copy of
![]() $F$
.
$F$
.
We are now ready to prove that
![]() $\tilde{q}(H) \le \frac{\delta (H)}{\Delta (F)} + 1$
. The above observation implies that the induced graph on each
$\tilde{q}(H) \le \frac{\delta (H)}{\Delta (F)} + 1$
. The above observation implies that the induced graph on each
![]() $\delta (H)$
-set has, in each colour, a vertex of degree at least
$\delta (H)$
-set has, in each colour, a vertex of degree at least
![]() $\Delta (F)$
. However, the average degree of the sparsest colour class in
$\Delta (F)$
. However, the average degree of the sparsest colour class in
![]() $\Gamma$
is at most
$\Gamma$
is at most
![]() $\frac{2 \left({N \atop 2}\right)}{qN}=\frac{N-1}{q} = \delta - 1$
. Thus, by Theorem5.3,
$\frac{2 \left({N \atop 2}\right)}{qN}=\frac{N-1}{q} = \delta - 1$
. Thus, by Theorem5.3,
![]() $\Gamma$
has a set of
$\Gamma$
has a set of
![]() $\frac{\Delta (F)N}{\delta (H)+\Delta (F)-1}$
vertices that induce a graph with maximum degree less than
$\frac{\Delta (F)N}{\delta (H)+\Delta (F)-1}$
vertices that induce a graph with maximum degree less than
![]() $\Delta (F)$
in this colour. Hence, we must have
$\Delta (F)$
in this colour. Hence, we must have
which rearranges to give
![]() $q \le \frac{\delta (H)+\Delta (F)-1}{\Delta (F)} - \frac{1}{\delta (H)-1} \leq \frac{\delta (H)}{\Delta (F)} + 1$
, from which the conclusion follows.
$q \le \frac{\delta (H)+\Delta (F)-1}{\Delta (F)} - \frac{1}{\delta (H)-1} \leq \frac{\delta (H)}{\Delta (F)} + 1$
, from which the conclusion follows.
We turn our attention to the second bound, namely
![]() $\tilde{q}(H) \le \frac{\delta (H)^2}{2 e(F)}$
. For any subset
$\tilde{q}(H) \le \frac{\delta (H)^2}{2 e(F)}$
. For any subset
![]() $U\subseteq V(\Gamma )$
of size
$U\subseteq V(\Gamma )$
of size
![]() $\delta (H)$
, there must be a colour
$\delta (H)$
, there must be a colour
![]() $i\in [q]$
such that there are at most
$i\in [q]$
such that there are at most
![]() $\frac{1}{q}\binom{\delta (H)}{2}$
edges of colour
$\frac{1}{q}\binom{\delta (H)}{2}$
edges of colour
![]() $i$
inside
$i$
inside
![]() $U$
. Using once again our observation above, we know that
$U$
. Using once again our observation above, we know that
![]() $\Gamma [U]$
contains a copy of
$\Gamma [U]$
contains a copy of
![]() $F$
in colour
$F$
in colour
![]() $i$
, and therefore we must have
$i$
, and therefore we must have
![]() $\frac{1}{q}\binom{\delta (H)}{2} \geq e(F)$
, which yields the claimed bound.
$\frac{1}{q}\binom{\delta (H)}{2} \geq e(F)$
, which yields the claimed bound.
We end this section with a proof of Theorem5.1(e).
Proof of Theorem
5.1(e). Let
![]() $p\gg \sqrt{\frac{\log n}{n}}$
and
$p\gg \sqrt{\frac{\log n}{n}}$
and
![]() $H\sim G(n,p)$
. By Lemma 2.1, it suffices to show that a.a.s.
$H\sim G(n,p)$
. By Lemma 2.1, it suffices to show that a.a.s.
![]() $H$
is not
$H$
is not
![]() $q$
-Ramsey simple for
$q$
-Ramsey simple for
![]() $q=2$
.
$q=2$
.
For this, following Lemma 4.5, we may assume that every edge in
![]() $H$
belongs to a triangle. Now suppose for a contradiction that
$H$
belongs to a triangle. Now suppose for a contradiction that
![]() $H$
is
$H$
is
![]() $2$
-Ramsey simple. Let
$2$
-Ramsey simple. Let
![]() $G$
be a minimal
$G$
be a minimal
![]() $2$
-Ramsey graph for
$2$
-Ramsey graph for
![]() $H$
such that
$H$
such that
![]() $G$
has a vertex
$G$
has a vertex
![]() $w$
with
$w$
with
![]() $d_G(w)=2\delta (H)-1$
. By the minimality of
$d_G(w)=2\delta (H)-1$
. By the minimality of
![]() $G$
, we can find an
$G$
, we can find an
![]() $H$
-free
$H$
-free
![]() $2$
-colouring
$2$
-colouring
![]() $c$
of the graph
$c$
of the graph
![]() $G-w$
. Now fix an arbitrary vertex
$G-w$
. Now fix an arbitrary vertex
![]() $v\in N_G(w)$
and observe that, by the pigeonhole principle, there must be a set
$v\in N_G(w)$
and observe that, by the pigeonhole principle, there must be a set
![]() $W\subseteq N_G(w) \setminus \{v\}$
of size
$W\subseteq N_G(w) \setminus \{v\}$
of size
![]() $\delta (H)-1$
such that all edges between
$\delta (H)-1$
such that all edges between
![]() $v$
and any of its neighbours in
$v$
and any of its neighbours in
![]() $W$
have the same colour; without loss of generality, let this be colour
$W$
have the same colour; without loss of generality, let this be colour
![]() $1$
and set
$1$
and set
![]() $U=W\cup \{v\}$
. We can extend the colouring
$U=W\cup \{v\}$
. We can extend the colouring
![]() $c$
by giving colour 1 to all edges from
$c$
by giving colour 1 to all edges from
![]() $w$
to
$w$
to
![]() $N_G(w) \setminus U$
and giving colour 2 to all edges from
$N_G(w) \setminus U$
and giving colour 2 to all edges from
![]() $w$
to vertices in
$w$
to vertices in
![]() $U$
. With this colouring we cannot create a monochromatic copy of
$U$
. With this colouring we cannot create a monochromatic copy of
![]() $H$
in colour 1, as
$H$
in colour 1, as
![]() $w$
is only incident to
$w$
is only incident to
![]() $\delta (H)-1$
edges of colour 1. On the other hand,
$\delta (H)-1$
edges of colour 1. On the other hand,
![]() $w$
is incident to exactly
$w$
is incident to exactly
![]() $\delta (H)$
edges of colour 2, which all lie between
$\delta (H)$
edges of colour 2, which all lie between
![]() $w$
and
$w$
and
![]() $U$
. Hence, if there were a monochromatic copy of
$U$
. Hence, if there were a monochromatic copy of
![]() $H$
in colour 2, the edge
$H$
in colour 2, the edge
![]() $wv$
would need to be part of it. However, since all edges in
$wv$
would need to be part of it. However, since all edges in
![]() $U$
involving
$U$
involving
![]() $v$
are of colour
$v$
are of colour
![]() $1$
, that means the edge
$1$
, that means the edge
![]() $wv$
is not contained in any triangle of colour
$wv$
is not contained in any triangle of colour
![]() $2$
, and hence cannot be in a monochromatic copy of
$2$
, and hence cannot be in a monochromatic copy of
![]() $H$
.
$H$
.
6. Concluding remarks and open problems
In this paper we built upon the work of Grinshpun [Reference Grinshpun17] and studied the
![]() $q$
-Ramsey simplicity of
$q$
-Ramsey simplicity of
![]() $H\sim G(n,p)$
for a wide range of values of
$H\sim G(n,p)$
for a wide range of values of
![]() $p$
and
$p$
and
![]() $q$
. We encountered three different types of behaviour: for very sparse ranges, i.e., when
$q$
. We encountered three different types of behaviour: for very sparse ranges, i.e., when
![]() $p\ll \frac{1}{n}$
or
$p\ll \frac{1}{n}$
or
![]() $\frac{\log n}{n} \ll p \ll n^{-\frac{2}{3}}$
, we showed that a.a.s.
$\frac{\log n}{n} \ll p \ll n^{-\frac{2}{3}}$
, we showed that a.a.s.
![]() $H$
is
$H$
is
![]() $q$
-Ramsey simple for every possible number of colours
$q$
-Ramsey simple for every possible number of colours
![]() $q$
; for much denser ranges, i.e., when
$q$
; for much denser ranges, i.e., when
![]() $p\gg \left (\frac{\log n}{n} \right )^{\frac{1}{2}}$
, a.a.s. we do not have Ramsey simplicity even when
$p\gg \left (\frac{\log n}{n} \right )^{\frac{1}{2}}$
, a.a.s. we do not have Ramsey simplicity even when
![]() $q=2$
; in between these ranges, when
$q=2$
; in between these ranges, when
![]() $n^{-\frac{2}{3}}\ll p \ll n^{-\frac{1}{2}}$
, there exists a finite threshold value
$n^{-\frac{2}{3}}\ll p \ll n^{-\frac{1}{2}}$
, there exists a finite threshold value
![]() $\tilde{q}(H) \ge 2$
on the number of colours
$\tilde{q}(H) \ge 2$
on the number of colours
![]() $q$
such that
$q$
such that
![]() $H$
is
$H$
is
![]() $q$
-Ramsey simple if and only if
$q$
-Ramsey simple if and only if
![]() $q\leq \tilde{q}(H)$
. We determined this threshold up to a constant or, when
$q\leq \tilde{q}(H)$
. We determined this threshold up to a constant or, when
![]() $p = n^{-\frac 12 - o(1)}$
, logarithmic factor. We note further that in the range
$p = n^{-\frac 12 - o(1)}$
, logarithmic factor. We note further that in the range
![]() $\frac{\log n}{n}\ll p\ll n^{-1/2}$
, we can actually show that the following stronger statement is true almost surely for the same values of
$\frac{\log n}{n}\ll p\ll n^{-1/2}$
, we can actually show that the following stronger statement is true almost surely for the same values of
![]() $q$
as in Theorem5.1: not only does there exist a minimal
$q$
as in Theorem5.1: not only does there exist a minimal
![]() $q$
-Ramsey graph for
$q$
-Ramsey graph for
![]() $H\sim G(n,p)$
that contains a vertex of degree
$H\sim G(n,p)$
that contains a vertex of degree
![]() $q(\delta (H)-1)+1$
, but we can actually show that there exist minimal
$q(\delta (H)-1)+1$
, but we can actually show that there exist minimal
![]() $q$
-Ramsey graphs with arbitrarily many vertices of this degree; we provide the details in the arXiv version of this paper.
$q$
-Ramsey graphs with arbitrarily many vertices of this degree; we provide the details in the arXiv version of this paper.
Several natural questions remain open. First, our main result does not provide any information on the Ramsey simplicity of
![]() $G(n,p)$
when
$G(n,p)$
when
![]() $p$
is between
$p$
is between
![]() $\frac{1}{n}$
and
$\frac{1}{n}$
and
![]() $\frac{\log n}{n}$
.
$\frac{\log n}{n}$
.
Question 6.1.
What can be said about
![]() $\tilde{q}(H)$
when
$\tilde{q}(H)$
when
![]() $H\sim G(n,p)$
and
$H\sim G(n,p)$
and
![]() $p = \Omega \left ( \frac{1}{n} \right )$
and
$p = \Omega \left ( \frac{1}{n} \right )$
and
![]() $ p = O \left ( \frac{\log n}{n} \right )$
? In particular, is
$ p = O \left ( \frac{\log n}{n} \right )$
? In particular, is
![]() $H$
a.a.s.
$H$
a.a.s.
![]() $2$
-Ramsey simple in this case?
$2$
-Ramsey simple in this case?
In the range
![]() $p\gg \frac{\log n}{n}$
our simplicity proofs rely heavily on the fact that a.a.s.
$p\gg \frac{\log n}{n}$
our simplicity proofs rely heavily on the fact that a.a.s.
![]() $H\sim G(n,p)$
is 3-connected, implying the existence of signal senders for
$H\sim G(n,p)$
is 3-connected, implying the existence of signal senders for
![]() $H$
, which in turn allow us to deduce a fairly general recipe for constructing suitable Ramsey graphs. When
$H$
, which in turn allow us to deduce a fairly general recipe for constructing suitable Ramsey graphs. When
![]() $p\ll \frac{1}{n}$
, we know that
$p\ll \frac{1}{n}$
, we know that
![]() $H\sim G(n,p)$
is a.a.s. a forest, and simplicity follows from the construction of Szabó, Zumstein, and Zürcher [Reference Szabó, Zumstein and Zürcher20], which works for certain bipartite graphs. When
$H\sim G(n,p)$
is a.a.s. a forest, and simplicity follows from the construction of Szabó, Zumstein, and Zürcher [Reference Szabó, Zumstein and Zürcher20], which works for certain bipartite graphs. When
![]() $\frac{1}{n} \ll p \ll \frac{\log n}{n}$
, however, the random graph
$\frac{1}{n} \ll p \ll \frac{\log n}{n}$
, however, the random graph
![]() $G(n,p)$
becomes more complex (in particular, it is non-bipartite) but it is not yet connected. As a result, resolving the aforementioned question will likely require new ideas.
$G(n,p)$
becomes more complex (in particular, it is non-bipartite) but it is not yet connected. As a result, resolving the aforementioned question will likely require new ideas.
Second, in the range between
![]() $p= \Omega \left({ n^{-\frac{1}{2}} }\right)$
and
$p= \Omega \left({ n^{-\frac{1}{2}} }\right)$
and
![]() $ p = O \left({ \left (\frac{\log n}{n}\right )^{\frac{1}{2}}}\right)$
, we proved that
$ p = O \left({ \left (\frac{\log n}{n}\right )^{\frac{1}{2}}}\right)$
, we proved that
![]() $\tilde{q}(H)=O(p^{-1})$
, which shows that the threshold value here is of smaller order than when
$\tilde{q}(H)=O(p^{-1})$
, which shows that the threshold value here is of smaller order than when
![]() $p = n^{-\frac 12 - o(1)}$
, as demonstrated in Corollary 5.2. However, we did not provide any nontrivial lower bounds, and we wonder if that might not be possible.
$p = n^{-\frac 12 - o(1)}$
, as demonstrated in Corollary 5.2. However, we did not provide any nontrivial lower bounds, and we wonder if that might not be possible.
Question 6.2.
Is it true that
![]() $H$
is a.a.s. not
$H$
is a.a.s. not
![]() $2$
-Ramsey simple when
$2$
-Ramsey simple when
![]() $H\sim G(n,p)$
with
$H\sim G(n,p)$
with
![]() $p= \Omega \left({ n^{-\frac{1}{2}} }\right)$
and
$p= \Omega \left({ n^{-\frac{1}{2}} }\right)$
and
![]() $ p = O \left({ \left (\frac{\log n}{n}\right )^{\frac{1}{2}}}\right)$
?
$ p = O \left({ \left (\frac{\log n}{n}\right )^{\frac{1}{2}}}\right)$
?
In this case, signal senders for
![]() $H$
do exist, but the neighbourhood of the minimum degree vertex becomes more complex than just a forest, making it difficult to construct a graph as described in Proposition 3.1. On the other hand, the presence of isolated vertices makes it likely that a more delicate argument than the one used in part (e) would be needed to show non-simplicity for smaller
$H$
do exist, but the neighbourhood of the minimum degree vertex becomes more complex than just a forest, making it difficult to construct a graph as described in Proposition 3.1. On the other hand, the presence of isolated vertices makes it likely that a more delicate argument than the one used in part (e) would be needed to show non-simplicity for smaller
![]() $q$
. Nevertheless, we tend to believe that a.a.s.
$q$
. Nevertheless, we tend to believe that a.a.s.
![]() $\tilde{q}(H)=1$
for all
$\tilde{q}(H)=1$
for all
![]() $p\gg n^{-\frac{1}{2}}$
.
$p\gg n^{-\frac{1}{2}}$
.
The bounds on
![]() $\tilde{q}(H)$
presented in Corollary 5.2 (a) and (c) are already quite close, but it would be interesting to close the remaining gaps.
$\tilde{q}(H)$
presented in Corollary 5.2 (a) and (c) are already quite close, but it would be interesting to close the remaining gaps.
Question 6.3.
Let
![]() $H\sim G(n,p)$
with
$H\sim G(n,p)$
with
![]() $n^{-2/3} \ll p \ll n^{-1/2}$
. What are the asymptotics of
$n^{-2/3} \ll p \ll n^{-1/2}$
. What are the asymptotics of
![]() $\tilde{q}(H)$
?
$\tilde{q}(H)$
?
In this range, as we have seen in Section 3, the question about
![]() $q$
-Ramsey simplicity is tightly linked to the problem of finding a
$q$
-Ramsey simplicity is tightly linked to the problem of finding a
![]() $q$
-coloured graph
$q$
-coloured graph
![]() $\Gamma$
on
$\Gamma$
on
![]() $q(\delta (H) - 1) + 1$
vertices such that the following holds: For every set
$q(\delta (H) - 1) + 1$
vertices such that the following holds: For every set
![]() $U \subseteq V(\Gamma )$
of
$U \subseteq V(\Gamma )$
of
![]() $\delta (H)$
vertices and for every colour
$\delta (H)$
vertices and for every colour
![]() $i \in [q]$
, there exists a copy
$i \in [q]$
, there exists a copy
![]() $F_{U,i}$
of
$F_{U,i}$
of
![]() $F=H[N(u)]$
in
$F=H[N(u)]$
in
![]() $\Gamma [U]$
whose edges are all of colour
$\Gamma [U]$
whose edges are all of colour
![]() $i$
. The proofs of our lower bounds in Section 5.1 are obtained by finding such
$i$
. The proofs of our lower bounds in Section 5.1 are obtained by finding such
![]() $\Gamma$
(with additional properties as given in Proposition 3.3) through explicit constructions or probabilistic arguments. In order to prove that a.a.s.
$\Gamma$
(with additional properties as given in Proposition 3.3) through explicit constructions or probabilistic arguments. In order to prove that a.a.s.
![]() $H$
is not
$H$
is not
![]() $q$
-Ramsey simple, it would suffice to prove that such
$q$
-Ramsey simple, it would suffice to prove that such
![]() $\Gamma$
does not exist, that is, every
$\Gamma$
does not exist, that is, every
![]() $q$
-coloured graph
$q$
-coloured graph
![]() $\Gamma$
on
$\Gamma$
on
![]() $q(\delta (H) - 1) + 1$
vertices contains at least one subset
$q(\delta (H) - 1) + 1$
vertices contains at least one subset
![]() $U \subseteq V(\Gamma )$
of size
$U \subseteq V(\Gamma )$
of size
![]() $\delta (H)$
such that
$\delta (H)$
such that
![]() $\Gamma [U]$
is missing a copy of
$\Gamma [U]$
is missing a copy of
![]() $F$
in at least one colour. Note that in the proof of our second bound in case (d) of Theorem5.1 we obtain such a result by a simple counting argument which guarantees that we cannot pack
$F$
in at least one colour. Note that in the proof of our second bound in case (d) of Theorem5.1 we obtain such a result by a simple counting argument which guarantees that we cannot pack
![]() $q$
copies of
$q$
copies of
![]() $F$
into any graph on
$F$
into any graph on
![]() $\delta (H)$
vertices. Related to this argument, it seems challenging to determine how many copies of a given random graph can be packed into a complete graph, leading us to suggest the following question.
$\delta (H)$
vertices. Related to this argument, it seems challenging to determine how many copies of a given random graph can be packed into a complete graph, leading us to suggest the following question.
Question 6.4.
Let
![]() $H\sim G(n,p)$
with
$H\sim G(n,p)$
with
![]() $0\lt p\lt 1$
. How many copies of
$0\lt p\lt 1$
. How many copies of
![]() $H$
can be packed into
$H$
can be packed into
![]() $K_n$
?
$K_n$
?
In the densest range, that is, when
![]() $p\gg \left (\frac{\log n}{n}\right )^{\frac{1}{2}}$
, we know that
$p\gg \left (\frac{\log n}{n}\right )^{\frac{1}{2}}$
, we know that
![]() $H\sim G(n,p)$
is a.a.s. not
$H\sim G(n,p)$
is a.a.s. not
![]() $q$
-Ramsey simple for any
$q$
-Ramsey simple for any
![]() $q\geq 2$
. We wonder, however, what the behaviour of
$q\geq 2$
. We wonder, however, what the behaviour of
![]() $s_q(H)$
in this case is; in particular, it would be interesting to determine whether
$s_q(H)$
in this case is; in particular, it would be interesting to determine whether
![]() $s_q(H)$
is still typically close to the easy lower bound
$s_q(H)$
is still typically close to the easy lower bound
![]() $q(\delta (H)-1)+1$
. Note that the answer is no if
$q(\delta (H)-1)+1$
. Note that the answer is no if
![]() $p=1$
and
$p=1$
and
![]() $q \ge 2$
, since
$q \ge 2$
, since
![]() $s_2(K_n)=(n-1)^2$
. However, when
$s_2(K_n)=(n-1)^2$
. However, when
![]() $\left (\frac{\log n}{n}\right )^{\frac{1}{2}}\ll p \ll 1$
, we do not know of any bounds other than the general ones mentioned in the introduction. In particular, we propose the following problem, similar to one posed by Grinshpun, Raina, and Sengupta [Reference Grinshpun, Raina and Sengupta16].
$\left (\frac{\log n}{n}\right )^{\frac{1}{2}}\ll p \ll 1$
, we do not know of any bounds other than the general ones mentioned in the introduction. In particular, we propose the following problem, similar to one posed by Grinshpun, Raina, and Sengupta [Reference Grinshpun, Raina and Sengupta16].
Question 6.5.
How large is
![]() $s_2(H)$
for
$s_2(H)$
for
![]() $H\sim G\left(n,\frac{1}{2}\right)$
a.a.s.?
$H\sim G\left(n,\frac{1}{2}\right)$
a.a.s.?
Related to the above discussion, we also note that our methods can be applied to the 2-colour asymmetric Ramsey setting, in which a graph
![]() $G$
is said to be
$G$
is said to be
![]() $2$
-Ramsey for a pair of graphs
$2$
-Ramsey for a pair of graphs
![]() $(H_1,H_2)$
if every red-/blue-colouring of its edges leads to a red copy of
$(H_1,H_2)$
if every red-/blue-colouring of its edges leads to a red copy of
![]() $H_1$
or a blue copy of
$H_1$
or a blue copy of
![]() $H_2$
. In this setting, we define minimal Ramsey graphs and the smallest minimum degree
$H_2$
. In this setting, we define minimal Ramsey graphs and the smallest minimum degree
![]() $s_2(H_1,H_2)$
in the obvious way; the general lower bound is replaced by
$s_2(H_1,H_2)$
in the obvious way; the general lower bound is replaced by
![]() $s_2(H_1,H_2)\geq \delta (H_1)+\delta (H_2)-1$
and again we call a pair
$s_2(H_1,H_2)\geq \delta (H_1)+\delta (H_2)-1$
and again we call a pair
![]() $(H_1,H_2)$
2-Ramsey simple if this lower bound is attained. Our constructions can be modified to show that for
$(H_1,H_2)$
2-Ramsey simple if this lower bound is attained. Our constructions can be modified to show that for
![]() $H_1\sim G(n,p_1)$
and
$H_1\sim G(n,p_1)$
and
![]() $H_2\sim G(n,p_2)$
the pair
$H_2\sim G(n,p_2)$
the pair
![]() $(H_1,H_2)$
is a.a.s. 2-Ramsey simple if
$(H_1,H_2)$
is a.a.s. 2-Ramsey simple if
![]() $\frac{\log n}{n} \ll p_1\leq p_2 \ll n^{-1/2}$
. When
$\frac{\log n}{n} \ll p_1\leq p_2 \ll n^{-1/2}$
. When
![]() $p_1,p_2\ll n^{-1}$
, then again a modification of the argument of Szabó, Zumstein, and Zürcher [Reference Szabó, Zumstein and Zürcher20] can be used to show that we a.a.s. have 2-Ramsey simplicity. Still, the following questions remain.
$p_1,p_2\ll n^{-1}$
, then again a modification of the argument of Szabó, Zumstein, and Zürcher [Reference Szabó, Zumstein and Zürcher20] can be used to show that we a.a.s. have 2-Ramsey simplicity. Still, the following questions remain.
Question 6.6.
Let
![]() $H_1\sim G(n,p_1)$
and
$H_1\sim G(n,p_1)$
and
![]() $H_2\sim G(n,p_2)$
with
$H_2\sim G(n,p_2)$
with
![]() $p_1\ll n^{-1}$
and
$p_1\ll n^{-1}$
and
![]() $\frac{\log n}{n} \ll p_2 \ll n^{-1/2}$
. Is the pair
$\frac{\log n}{n} \ll p_2 \ll n^{-1/2}$
. Is the pair
![]() $(H_1,H_2)$
a.a.s. 2-Ramsey simple? What happens if one of the graphs comes from the dense range?
$(H_1,H_2)$
a.a.s. 2-Ramsey simple? What happens if one of the graphs comes from the dense range?
We also remark that our ideas from Section 5.1 can be used to resolve a special case of a conjecture due to Grinshpun [Reference Grinshpun17], stating that all triangle-free graphs are
![]() $2$
-Ramsey simple. In [Reference Grinshpun, Raina and Sengupta16], Grinshpun, Raina, and Sengupta use a construction similar to ours to show that the conjecture is true for all regular 3-connected triangle-free graphs satisfying one extra technical condition. Our approach allows us to prove that every well-behaved triangle-free graph is
$2$
-Ramsey simple. In [Reference Grinshpun, Raina and Sengupta16], Grinshpun, Raina, and Sengupta use a construction similar to ours to show that the conjecture is true for all regular 3-connected triangle-free graphs satisfying one extra technical condition. Our approach allows us to prove that every well-behaved triangle-free graph is
![]() $q$
-Ramsey simple for any
$q$
-Ramsey simple for any
![]() $q\geq 2$
.
$q\geq 2$
.
Finally, let us emphasise that there has been little study of (minimal) Ramsey graphs for
![]() $G(n,p)$
. The only results we are aware of concern the Ramsey number of
$G(n,p)$
. The only results we are aware of concern the Ramsey number of
![]() $G(n,p)$
, as mentioned in Section 1.2. Hence, as a more general direction for future research, it would be interesting to explore other aspects of the Ramsey behaviour of
$G(n,p)$
, as mentioned in Section 1.2. Hence, as a more general direction for future research, it would be interesting to explore other aspects of the Ramsey behaviour of
![]() $G(n,p)$
as the target graph.
$G(n,p)$
as the target graph.
Acknowledgements
The first author was supported by the Deutsche Forschungsgemeinschaft Graduiertenkolleg ‘Facets of Complexity’ (GRK 2434). The third author was supported by the Deutsche Forschungsgemeinschaft project 415310276 and by the NSTC grant 111-2115-M-002-009-MY2.
We would like to thank the anonymous referees for providing many helpful comments that improved the presentation of the paper.
Competing interests
The authors declare none.
A. Forests are Ramsey simple
Lemma A.1.
For every forest
![]() $F$
without isolated vertices and every integer
$F$
without isolated vertices and every integer
![]() $q\geq 2$
, we have
$q\geq 2$
, we have
![]() $s_q(F)=1$
.
$s_q(F)=1$
.
For two colours, Lemma A.1 follows from the general result for bipartite graphs of Szabó, Zumstein, and Zürcher [Reference Szabó, Zumstein and Zürcher20, Theorem 1.3 and Corollary 1.5]. Their proof generalises easily to more colours. For the sake of completeness, we include a simplified version of that proof here, dealing only with the case of forests.
Proof. Given
![]() $F$
, fix a bipartition
$F$
, fix a bipartition
![]() $V(F)=A\cup B$
, where
$V(F)=A\cup B$
, where
![]() $|A|\leq |B|$
and the size of
$|A|\leq |B|$
and the size of
![]() $A$
is minimised. Set
$A$
is minimised. Set
![]() $a=|A|$
,
$a=|A|$
,
![]() $b=|B|$
,
$b=|B|$
,
![]() $B_1=\{v\in B\,:\, d_F(v)=1\}$
, and
$B_1=\{v\in B\,:\, d_F(v)=1\}$
, and
![]() $B_{\geq 2}=B\setminus B_1$
. We start by showing that
$B_{\geq 2}=B\setminus B_1$
. We start by showing that
![]() $|B_{\geq 2}|\leq a-1$
. Indeed, let
$|B_{\geq 2}|\leq a-1$
. Indeed, let
![]() $T_1,\ldots, T_k$
be the components of
$T_1,\ldots, T_k$
be the components of
![]() $F$
and, for each
$F$
and, for each
![]() $i\in [k]$
, let
$i\in [k]$
, let
![]() $r_i$
be an arbitrary vertex in
$r_i$
be an arbitrary vertex in
![]() $A\cap V(T_i)$
. Viewing
$A\cap V(T_i)$
. Viewing
![]() $T_i$
as a tree rooted at
$T_i$
as a tree rooted at
![]() $r_i$
, we note that each element of
$r_i$
, we note that each element of
![]() $B_{\geq 2}\cap V(T_i)$
must have a child in
$B_{\geq 2}\cap V(T_i)$
must have a child in
![]() $A\cap V(T_i)$
and, since
$A\cap V(T_i)$
and, since
![]() $T_i$
is a tree, all of these children must be different. Thus,
$T_i$
is a tree, all of these children must be different. Thus,
![]() $|A\cap V(T_i)|\geq |B_{\geq 2}\cap V(T_i)|+1$
for all
$|A\cap V(T_i)|\geq |B_{\geq 2}\cap V(T_i)|+1$
for all
![]() $i\in [k]$
, and summing up over all components yields
$i\in [k]$
, and summing up over all components yields
![]() $|A|\geq |B_{\geq 2}|+1$
.
$|A|\geq |B_{\geq 2}|+1$
.
Now, set
![]() $r=q(a-1), s=q^{r+1}v(F),$
and
$r=q(a-1), s=q^{r+1}v(F),$
and
![]() $t=sbq$
, and let
$t=sbq$
, and let
![]() $G$
be the graph constructed as follows:
$G$
be the graph constructed as follows:
-
• let
 $V(G)=X\dot{\cup } Y\dot{\cup } Z$
, where
$V(G)=X\dot{\cup } Y\dot{\cup } Z$
, where
 $|{X}| = r$
,
$|{X}| = r$
,
 $|{Y}| = s$
, and
$|{Y}| = s$
, and
 $|{Z}| = t$
,
$|{Z}| = t$
, -
• add a complete bipartite graph between
 $X$
and
$X$
and
 $Y$
, and
$Y$
, and -
• partition
 $Z$
into
$Z$
into
 $s$
subsets of size
$s$
subsets of size
 $bq$
, indexed by the elements of
$bq$
, indexed by the elements of
 $Y$
. That is, let
$Y$
. That is, let
 $Z = \bigcup \limits _{y\in Y}Z_y$
, where
$Z = \bigcup \limits _{y\in Y}Z_y$
, where
 $|{Z_y}| = bq$
. For each
$|{Z_y}| = bq$
. For each
 $y\in Y$
, connect
$y\in Y$
, connect
 $y$
to all vertices of
$y$
to all vertices of
 $Z_y$
.
$Z_y$
.
Each vertex
![]() $v\in Z$
then satisfies
$v\in Z$
then satisfies
![]() $d_G(v)=1$
. We will now show that (i)
$d_G(v)=1$
. We will now show that (i)
![]() $G - Z \not \rightarrow _q F$
, and (ii)
$G - Z \not \rightarrow _q F$
, and (ii)
![]() $G \rightarrow _q F$
. From this it follows directly that
$G \rightarrow _q F$
. From this it follows directly that
![]() $G$
must contain a graph from
$G$
must contain a graph from
![]() $\mathcal{M}_q(F)$
with minimum degree one, and hence that
$\mathcal{M}_q(F)$
with minimum degree one, and hence that
![]() $s_q(F)=1$
.
$s_q(F)=1$
.
To see property (i), colour
![]() $E(G-Z)$
as follows: take any partition
$E(G-Z)$
as follows: take any partition
![]() $X=X_1\cup \ldots \cup X_q$
with
$X=X_1\cup \ldots \cup X_q$
with
![]() $|X_i|=a-1$
for every
$|X_i|=a-1$
for every
![]() $i\in [q]$
, and colour
$i\in [q]$
, and colour
![]() $E(X_i,Y)$
in colour
$E(X_i,Y)$
in colour
![]() $i$
. Then each colour class is a bipartite graph with a partite set of size smaller than
$i$
. Then each colour class is a bipartite graph with a partite set of size smaller than
![]() $a$
. By the definition of
$a$
. By the definition of
![]() $a$
, there cannot be a monochromatic copy of
$a$
, there cannot be a monochromatic copy of
![]() $F$
.
$F$
.
We prove (ii) next. Consider any
![]() $q$
-colouring
$q$
-colouring
![]() $\varphi\,:\, E(G)\rightarrow [q]$
. Each vertex
$\varphi\,:\, E(G)\rightarrow [q]$
. Each vertex
![]() $y\in Y$
has
$y\in Y$
has
![]() $bq$
neighbours in
$bq$
neighbours in
![]() $Z_y$
, and hence there must be a subset
$Z_y$
, and hence there must be a subset
![]() $Z_y^{\prime}\subseteq Z_y$
of size
$Z_y^{\prime}\subseteq Z_y$
of size
![]() $b$
such that the edges from
$b$
such that the edges from
![]() $y$
to
$y$
to
![]() $Z_y^{\prime}$
are monochromatic. As we use only
$Z_y^{\prime}$
are monochromatic. As we use only
![]() $q$
colours, there must be a subset
$q$
colours, there must be a subset
![]() $Y^{\prime}\subseteq Y$
of
$Y^{\prime}\subseteq Y$
of
![]() $\frac{s}{q}$
vertices
$\frac{s}{q}$
vertices
![]() $y_1,\ldots, y_{s/q}$
such that, without loss of generality, the edges between
$y_1,\ldots, y_{s/q}$
such that, without loss of generality, the edges between
![]() $y_i$
and
$y_i$
and
![]() $Z_{y_i}^{\prime}$
are all colour
$Z_{y_i}^{\prime}$
are all colour
![]() $1$
for each
$1$
for each
![]() $i \in [s/q]$
. Further, set
$i \in [s/q]$
. Further, set
![]() $Z^{\prime}=\bigcup \limits _{y_i\in Y^{\prime}} Z_{y_i}^{\prime}$
. Next, let
$Z^{\prime}=\bigcup \limits _{y_i\in Y^{\prime}} Z_{y_i}^{\prime}$
. Next, let
![]() $X=\{x_1,\ldots, x_r\}$
. For every
$X=\{x_1,\ldots, x_r\}$
. For every
![]() $y_i\in Y^{\prime}$
, we consider the vector
$y_i\in Y^{\prime}$
, we consider the vector
![]() $c_i\,:\!=\,(\varphi (x_1y_i),\ldots, \varphi (x_ry_i))\in [q]^r$
, the colour profile of
$c_i\,:\!=\,(\varphi (x_1y_i),\ldots, \varphi (x_ry_i))\in [q]^r$
, the colour profile of
![]() $y_i$
. As
$y_i$
. As
![]() $|Y^{\prime}|=s/q = q^r v(F)$
, there must be at least
$|Y^{\prime}|=s/q = q^r v(F)$
, there must be at least
![]() $v(F)$
vertices in
$v(F)$
vertices in
![]() $Y^{\prime}$
with the same colour profile
$Y^{\prime}$
with the same colour profile
![]() $c$
. By symmetry, we may assume that
$c$
. By symmetry, we may assume that
![]() $c_1=c_2=\ldots =c_{v(F)}=c$
. We consider two cases.
$c_1=c_2=\ldots =c_{v(F)}=c$
. We consider two cases.
Case 1: There is a colour
![]() $i\in [q]$
that appears at least
$i\in [q]$
that appears at least
![]() $a$
times in
$a$
times in
![]() $c$
. This gives a copy of
$c$
. This gives a copy of
![]() $K_{a,v(F)}$
between
$K_{a,v(F)}$
between
![]() $X$
and
$X$
and
![]() $\{y_1,\ldots, y_{v(F)}\}$
that is monochromatic in colour
$\{y_1,\ldots, y_{v(F)}\}$
that is monochromatic in colour
![]() $i$
. As
$i$
. As
![]() $K_{a,v(F)}$
contains a copy of
$K_{a,v(F)}$
contains a copy of
![]() $F$
, we are done.
$F$
, we are done.
Case 2: Every colour is used exactly
![]() $(a-1)$
times in
$(a-1)$
times in
![]() $c$
. In particular, we find a subset
$c$
. In particular, we find a subset
![]() $X^{\prime}\subseteq X$
of size
$X^{\prime}\subseteq X$
of size
![]() $a-1$
such that the edges between
$a-1$
such that the edges between
![]() $X^{\prime}$
and
$X^{\prime}$
and
![]() $\{y_1,\ldots, y_{v(F)}\}$
are monochromatic in colour
$\{y_1,\ldots, y_{v(F)}\}$
are monochromatic in colour
![]() $1$
. Using the edges between
$1$
. Using the edges between
![]() $y_i$
and
$y_i$
and
![]() $Z_{y_i}^{\prime}$
, for
$Z_{y_i}^{\prime}$
, for
![]() $i\in [v(F)]$
, we find a monochromatic copy of
$i\in [v(F)]$
, we find a monochromatic copy of
![]() $F$
: embed
$F$
: embed
![]() $A$
into
$A$
into
![]() $\{y_1,\ldots, y_{v(F)}\}$
arbitrarily, embed
$\{y_1,\ldots, y_{v(F)}\}$
arbitrarily, embed
![]() $B_1$
into
$B_1$
into
![]() $Z^{\prime}$
by respecting the adjacency relation, and embed
$Z^{\prime}$
by respecting the adjacency relation, and embed
![]() $B_{\geq 2}$
into
$B_{\geq 2}$
into
![]() $X^{\prime}$
arbitrarily.
$X^{\prime}$
arbitrarily.