Hostname: page-component-cb9f654ff-5kfdg Total loading time: 0 Render date: 2025-08-07T06:54:25.022Z Has data issue: false hasContentIssue false
  • English
  • Français

Planting Colourings Silently

Part of: Graph theory

Published online by Cambridge University Press:  07 December 2016

VICTOR BAPST ,
AMIN COJA-OGHLAN  and
CHARILAOS EFTHYMIOU
VICTOR BAPST
Affiliation:
Mathematics Institute, Goethe University, 10 Robert Mayer St, Frankfurt 60325, Germany (e-mail: bapst@math.uni-frankfurt.de, acoghlan@math.uni-frankfurt.de, efthymiou@math.uni-frankfurt.de)
AMIN COJA-OGHLAN
Affiliation:
Mathematics Institute, Goethe University, 10 Robert Mayer St, Frankfurt 60325, Germany (e-mail: bapst@math.uni-frankfurt.de, acoghlan@math.uni-frankfurt.de, efthymiou@math.uni-frankfurt.de)
CHARILAOS EFTHYMIOU
Affiliation:
Mathematics Institute, Goethe University, 10 Robert Mayer St, Frankfurt 60325, Germany (e-mail: bapst@math.uni-frankfurt.de, acoghlan@math.uni-frankfurt.de, efthymiou@math.uni-frankfurt.de)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let k ⩾ 3 be a fixed integer and let Zk (G) be the number of k-colourings of the graph G. For certain values of the average degree, the random variable Zk (G(n, m)) is known to be concentrated in the sense that 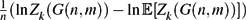$\tfrac{1}{n}(\ln Z_k(G(n,m))-\ln\Erw[Z_k(G(n,m))])$ converges to 0 in probability (Achlioptas and Coja-Oghlan, Proc. FOCS 2008). In the present paper we prove a significantly stronger concentration result. Namely, we show that for a wide range of average degrees, 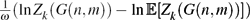$\tfrac{1}{\omega}(\ln Z_k(G(n,m))-\ln\Erw[Z_k(G(n,m))])$ converges to 0 in probability for any diverging function 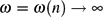$\omega=\omega(n)\ra\infty$ . For k exceeding a certain constant k 0 this result covers all average degrees up to the so-called condensation phase transitiond k,con , and this is best possible. As an application, we show that the experiment of choosing a k-colouring of the random graph G(n,m) uniformly at random is contiguous with respect to the so-called ‘planted model’.

MSC classification

Primary: 05C80: Random graphs
Secondary: 05C15: Coloring of graphs and hypergraphs

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 26 , Issue 3 , May 2017 , pp. 338 - 366
Copyright
Copyright © Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[1] Achlioptas, D. and Coja-Oghlan, A. (2008) Algorithmic barriers from phase transitions. In Proc. 49th FOCS, pp. 793–802.Google Scholar
[2] Achlioptas, D. and Friedgut, E. (1999) A sharp threshold for k-colorability. Random Struct. Alg. 14 63–70.3.0.CO;2-7>CrossRefGoogle Scholar
[3] Achlioptas, D. and Molloy, M. (1997) The analysis of a list-coloring algorithm on a random graph. In Proc. 38th FOCS, pp. 204–212.CrossRefGoogle Scholar
[4] Achlioptas, D. and Moore, C. (2004) The chromatic number of random regular graphs. In Proc. 8th RANDOM, pp. 219–228.Google Scholar
[5] Achlioptas, D. and Naor, A. (2005) The two possible values of the chromatic number of a random graph. Ann. of Math. 162 1333–1349.Google Scholar
[6] Alon, N. and Krivelevich, M. (1997) The concentration of the chromatic number of random graphs. Combinatorica 17 303–313.Google Scholar
[7] Banks, J. and Moore, C. Information-theoretic thresholds for community detection in sparse networks. arXiv:1601.02658 Google Scholar
[8] Bapst, V., Coja-Oghlan, A., Hetterich, S., Raßmann, F. and Vilenchik, D. (2016) The condensation phase transition in random graph coloring. Comm. Math. Phys. 341 543–606.Google Scholar
[9] Bollobás, B. (1988) The chromatic number of random graphs. Combinatorica 8 49–55 CrossRefGoogle Scholar
[10] Bollobás, B. (2001) Random Graphs, second edition, Cambridge University Press.Google Scholar
[11] Coja-Oghlan, A. (2013) Upper-bounding the k-colorability threshold by counting covers. Electron. J. Combin. 20 P32.CrossRefGoogle Scholar
[12] Coja-Oghlan, A., Efthymiou, C. and Hetterich, S. (2016) On the chromatic number of random regular graphs. J. Combin. Theory Ser. B 116 367–439.Google Scholar
[13] Coja-Oghlan, A. and Pachon-Pinzon, A. Y. (2012) The decimation process in random k-SAT. SIAM J. Discrete Math. 26 1471–1509.Google Scholar
[14] Coja-Oghlan, A. and Panagiotou, K. (2016) Going after the k-SAT threshold. In Proc. 45th STOC 2013, pp. 705–714, and Adv. Math. 288 985–1068.Google Scholar
[15] Coja-Oghlan, A. and Vilenchik, D. (2013) Chasing the k-colorability threshold. In Proc. 54th FOCS, pp. 380–389. A full version is available as arXiv:1304.1063 Google Scholar
[16] Efthymiou, C. (2014) Switching colouring of G(n, d/n) for sampling up to Gibbs uniqueness threshold. In Proc. 22nd ESA, pp. 371–281.Google Scholar
[17] Erdős, P. and Rényi, A. (1960) On the evolution of random graphs. Magyar Tud. Akad. Mat. Kutató Int. Közl. 5 17–61.Google Scholar
[18] Grimmett, G. and McDiarmid, C. (1975) On colouring random graphs. Math. Proc. Cambridge Phil. Soc. 77 313–324 Google Scholar
[19] Janson, S. (1995) Random regular graphs: Asymptotic distributions and contiguity. Combin. Probab. Comput. 4 369–405.CrossRefGoogle Scholar
[20] Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley.Google Scholar
[21] Kemkes, G., Perez-Gimenez, X. and Wormald, N. (2010) On the chromatic number of random d-regular graphs. Adv. Math. 223 300–328.Google Scholar
[22] Krivelevich, M. and Sudakov, B. (1998) Coloring random graphs. Inform. Process. Lett. 67 71–74 Google Scholar
[23] Krzakala, F., Montanari, A., Ricci-Tersenghi, F., Semerjian, G. and Zdeborova, L. (2007) Gibbs states and the set of solutions of random constraint satisfaction problems. Proc. Nat. Acad. Sci. 104 10318–10323.Google Scholar
[24] Krzakala, F., Pagnani, A. and Weigt, M. (2004) Threshold values, stability analysis and high-q asymptotics for the coloring problem on random graphs. Phys. Rev. E 70 046705.Google Scholar
[25] Krzakala, F. and Zdeborová, L. (2009) Hiding quiet solutions in random constraint satisfaction problems. Phys. Rev. Lett. 102 238701.CrossRefGoogle ScholarPubMed
[26] Łuczak, T. (1991) The chromatic number of random graphs. Combinatorica 11 45–54 Google Scholar
[27] Łuczak, T. (1991) A note on the sharp concentration of the chromatic number of random graphs. Combinatorica 11 295–297 CrossRefGoogle Scholar
[28] Matula, D. (1987) Expose-and-merge exploration and the chromatic number of a random graph. Combinatorica 7 275–284.Google Scholar
[29] McDiarmid, C. (1998) Concentration. In Probabilistic Methods for Algorithmic Discrete Mathematics (Habib, M. et al., eds), Springer, pp. 195–248.Google Scholar
[30] Mézard, M. and Montanari, A. (2009) Information, Physics and Computation, Oxford University Press.Google Scholar
[31] Molloy, M. (2012) The freezing threshold for k-colourings of a random graph. In Proc. 43rd STOC, pp. 921–930.Google Scholar
[32] Molloy, M. and Restrepo, R. (2013) Frozen variables in random boolean constraint satisfaction problems. In Proc. 24th SODA, pp. 1306–1318.Google Scholar
[33] Montanari, A., Restrepo, R. and Tetali, P. (2011) Reconstruction and clustering in random constraint satisfaction problems. SIAM J. Discrete Math. 25 771–808.Google Scholar
[34] Mulet, R., Pagnani, A., Weigt, M. and Zecchina, R. (2002) Coloring random graphs. Phys. Rev. Lett. 89 268701.Google Scholar
[35] Neeman, J. and Netrapalli, P. Non-reconstructability in the stochastic block model. arXiv:1404.6304 Google Scholar
[36] Robinson, R. and Wormald, N. (1994) Almost all regular graphs are Hamiltonian. Random Struct. Alg. 5 363–374.Google Scholar
[37] Shamir, E. and Spencer, J. (1987) Sharp concentration of the chromatic number of random graphs G(n, p). Combinatorica 7 121–129 Google Scholar
[38] Zdeborová, L. and Krzakala, F. (2007) Phase transition in the coloring of random graphs. Phys. Rev. E 76 031131.Google Scholar