Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dudek, Andrzej
and
Prałat, Paweł
2017.
On some Multicolor Ramsey Properties of Random Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 31,
Issue. 3,
p.
2079.
Clemens, Dennis
Jenssen, Matthew
Kohayakawa, Yoshiharu
Morrison, Natasha
Mota, Guilherme Oliveira
Reding, Damian
and
Roberts, Barnaby
2017.
Número de Ramsey relativo a arestas de potências de caminhos.
p.
85.
Dudek, Andrzej
Khoeini, Farideh
and
Prałat, Paweł
2018.
Size-Ramsey numbers of cycles versus a path.
Discrete Mathematics,
Vol. 341,
Issue. 7,
p.
2095.
Lu, Linyuan
and
Wang, Zhiyu
2018.
On the Size-Ramsey Number of Tight Paths.
SIAM Journal on Discrete Mathematics,
Vol. 32,
Issue. 3,
p.
2172.
Javadi, R.
Khoeini, F.
Omidi, G. R.
and
Pokrovskiy, A.
2019.
On the Size-Ramsey Number of Cycles.
Combinatorics, Probability and Computing,
Vol. 28,
Issue. 06,
p.
871.
Clemens, Dennis
Jenssen, Matthew
Kohayakawa, Yoshiharu
Morrison, Natasha
Mota, Guilherme Oliveira
Reding, Damian
and
Roberts, Barnaby
2019.
The size‐Ramsey number of powers of paths.
Journal of Graph Theory,
Vol. 91,
Issue. 3,
p.
290.
Frieze, Alan
Pérez‐Giménez, Xavier
Prałat, Paweł
and
Reiniger, Benjamin
2019.
Perfect matchings and Hamiltonian cycles in the preferential attachment model.
Random Structures & Algorithms,
Vol. 54,
Issue. 2,
p.
258.
Kohayakawa, Yoshiharu
Retter, Troy
and
Rödl, Vojtěch
2019.
The size Ramsey number of short subdivisions of bounded degree graphs.
Random Structures & Algorithms,
Vol. 54,
Issue. 2,
p.
304.
DeBiasio, Louis
and
McKenney, Paul
2019.
Density of Monochromatic Infinite Subgraphs.
Combinatorica,
Vol. 39,
Issue. 4,
p.
847.
Liu, Meng
and
Li, Yusheng
2019.
Bipartite Ramsey numbers of paths for random graphs.
Discrete Applied Mathematics,
Vol. 254,
Issue. ,
p.
171.
Krivelevich, Michael
2019.
Long Cycles in Locally Expanding Graphs, with Applications.
Combinatorica,
Vol. 39,
Issue. 1,
p.
135.
Bennett, Patrick
DeBiasio, Louis
Dudek, Andrzej
and
English, Sean
2019.
Large monochromatic components and long monochromatic cycles in random hypergraphs.
European Journal of Combinatorics,
Vol. 76,
Issue. ,
p.
123.
Balogh, József
Clemen, Felix Christian
Heath, Emily
and
Lavrov, Mikhail
2020.
Ordered size Ramsey number of paths.
Discrete Applied Mathematics,
Vol. 276,
Issue. ,
p.
13.
Han, Jie
Jenssen, Matthew
Kohayakawa, Yoshiharu
Mota, Guilherme Oliveira
and
Roberts, Barnaby
2020.
The multicolour size-Ramsey number of powers of paths.
Journal of Combinatorial Theory, Series B,
Vol. 145,
Issue. ,
p.
359.
Clemens, Dennis
Miralaei, Meysam
Reding, Damian
Schacht, Mathias
and
Taraz, Anusch
2021.
On the size-Ramsey number of grid graphs.
Combinatorics, Probability and Computing,
Vol. 30,
Issue. 5,
p.
670.
Berger, Sören
Kohayakawa, Yoshiharu
Maesaka, Giulia Satiko
Martins, Taísa
Mendonça, Walner
Mota, Guilherme Oliveira
and
Parczyk, Olaf
2021.
The size‐Ramsey number of powers of bounded degree trees.
Journal of the London Mathematical Society,
Vol. 103,
Issue. 4,
p.
1314.
You, Chun-lin
2021.
Lower Bounds of Size Ramsey Number for Graphs with Small Independence Number.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 37,
Issue. 4,
p.
841.
Pérez-Giménez, Xavier
Prałat, Paweł
and
West, Douglas B.
2021.
On-line size Ramsey number for monotone k-uniform ordered paths with uniform looseness.
European Journal of Combinatorics,
Vol. 92,
Issue. ,
p.
103242.
Draganić, Nemanja
Krivelevich, Michael
and
Nenadov, Rajko
2021.
The size‐Ramsey number of short subdivisions.
Random Structures & Algorithms,
Vol. 59,
Issue. 1,
p.
68.
Liu, Meng
and
Li, Yusheng
2021.
Bipartite Ramsey Numbers of Cycles for Random Graphs.
Graphs and Combinatorics,
Vol. 37,
Issue. 6,
p.
2703.
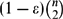 $(1-\varepsilon)\binom{n}{2}$ edges, whenever G is 2-edge-coloured, there is a monochromatic path of length at least
$(1-\varepsilon)\binom{n}{2}$ edges, whenever G is 2-edge-coloured, there is a monochromatic path of length at least 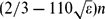 $(2/3 - 110\sqrt{\varepsilon})n$ . This is an extension of the classical result by Gerencsér and Gyárfás which says that whenever Kn is 2-coloured there is a monochromatic path of length at least 2n/3.
$(2/3 - 110\sqrt{\varepsilon})n$ . This is an extension of the classical result by Gerencsér and Gyárfás which says that whenever Kn is 2-coloured there is a monochromatic path of length at least 2n/3.
