Hostname: page-component-cb9f654ff-pvkqz Total loading time: 0 Render date: 2025-08-06T23:51:10.429Z Has data issue: false hasContentIssue false
  • English
  • Français

On Turán exponents of bipartite graphs

Part of: Graph theory

Published online by Cambridge University Press:  04 August 2021

Tao Jiang ,
Jie Ma  and
Liana Yepremyan
Tao Jiang*
Affiliation:
Department of Mathematics, Miami University, Oxford, OH 45056, USA. Research supported in part by National Science Foundation grants DMS-1400249 and DMS-1855542
Jie Ma
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, Hefei, 230026, China. Research supported in part by National Key Research and Development Project SQ2020YFA070080, National Natural Science Foundation of China grants 11501539 and 11622110, and Anhui Initiative in Quantum Information Technologies grant AHY150200
Liana Yepremyan
Affiliation:
Department of Mathematics, University of Oxford, UK. Research supported in part by ERC Consolidator Grant 647678
*
*Corresponding author. Email: jiangt@miamioh.edu.
Get access Rights & Permissions [Opens in a new window]

Abstract

A long-standing conjecture of Erdős and Simonovits asserts that for every rational number 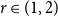$r\in (1,2)$ there exists a bipartite graph H such that 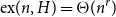$\mathrm{ex}(n,H)=\Theta(n^r)$. So far this conjecture is known to be true only for rationals of form 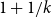$1+1/k$ and 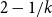$2-1/k$, for integers 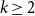$k\geq 2$. In this paper, we add a new form of rationals for which the conjecture is true: 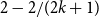$2-2/(2k+1)$, for 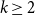$k\geq 2$. This in turn also gives an affirmative answer to a question of Pinchasi and Sharir on cube-like graphs. Recently, a version of Erdős and Simonovits$^{\prime}$s conjecture, where one replaces a single graph by a finite family, was confirmed by Bukh and Conlon. They proposed a construction of bipartite graphs which should satisfy Erdős and Simonovits$^{\prime}$s conjecture. Our result can also be viewed as a first step towards verifying Bukh and Conlon$^{\prime}$s conjecture. We also prove an upper bound on the Turán number of theta graphs in an asymmetric setting and employ this result to obtain another new rational exponent for Turán exponents: 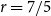$r=7/5$.

Keywords

Turán numberTurán exponentextremal functioncube

MSC classification

Primary: 05C35: Extremal problems

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 2 , March 2022 , pp. 333 - 344
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alon, N., Rónyai, L. and Szabó, T. (1999) Norm-graphs: Variations and applications. J. Combin. Theory Ser. B 76 280–290.10.1006/jctb.1999.1906CrossRefGoogle Scholar
Blagojević, P. V. M., Bukh, B. and Karasev, R. (2013) Turán numbers for $K_{s,t}$ -free graphs: Topological obstructions and algebraic constructions. Israel J. Math. 197 199–214.10.1007/s11856-012-0184-zCrossRefGoogle Scholar
Bukh, B. (2015) Random algebraic construction of extremal graphs. Bull. Lond. Math. Soc. 47 939–945.Google Scholar
Bukh, B. and Conlon, D. (2018) Rational exponents in extremal graph theory. J. Eur. Math. Soc. 20 1747–1757.10.4171/JEMS/798CrossRefGoogle Scholar
Bukh, B. and Tait, M. (2020) Turán number of theta graphs. Combin. Probab. Comput. 29 495–507.10.1017/S0963548320000012CrossRefGoogle Scholar
Brown, W. G. (1966) On graphs that do not contain a Thomsen graph. Canad. Math. Bull. 9 281–285.10.4153/CMB-1966-036-2CrossRefGoogle Scholar
Conlon, D. (2019) Graphs with few paths of prescribed length between any two vertices. Bull. Lond. Math. Soc. 51 1015–1021.10.1112/blms.12295CrossRefGoogle Scholar
Conlon, D., Janzer, O. and Lee, J. More on the extremal number of subdivisions. Combinatorica, to appear. See also arXiv.org:1903.10631Google Scholar
Conlon, D. and Lee, J. On the extremal number of subdivisions. Int. Math. Res. Not., to appear.Google Scholar
Erdős, P. (1981) On the combinatorial problems that I would most like to see solved. Combinatorica 1 25–42.10.1007/BF02579174CrossRefGoogle Scholar
Erdős, P., Rényi, A. and Sós, V. T. (1966) On a problem of graph theory. Studia Sci. Math. Hungar. 1 215–235.Google Scholar
Erdős, P. and Simonovits, M. (1966) A limit theorem in graph theory. Studia Sci. Math. Hungar. 1 51–57.Google Scholar
Erdős, P. and Simonovits, M. (1970) Some extremal problems in graph theory. In Combinatorial Theory and Its Applications 1 (Proc. Colloq. Balatonfüred, 1969), North Holland, pp. 370–390.Google Scholar
Erdős, P. and Stone, H. (1946) On the structure of linear graphs. Bull. Amer. Math. Soc. 52 1087–1091.10.1090/S0002-9904-1946-08715-7CrossRefGoogle Scholar
Faudree, R. and Simonovits, M. (1983) On a class of degenerate extremal graph problems. Combinatorica 3 83–93.10.1007/BF02579343CrossRefGoogle Scholar
Frankl, P. (1986) All rationals occur as exponents. J. Combin. Theory Ser. A 42 200–206.10.1016/0097-3165(86)90090-7CrossRefGoogle Scholar
Füredi, Z. (1996) An upper bound on Zarankiewicz $^{\prime}$ problem. Combin. Probab. Comput. 1 29–33.10.1017/S0963548300001814CrossRefGoogle Scholar
Füredi, Z. (1996) New asymptotics for bipartite Turán numbers. J. Combin. Theory Ser. A 75 141–144.10.1006/jcta.1996.0067CrossRefGoogle Scholar
Füredi, Z. On a Theorem of Erdős and Simonovits on Graphs not Containing the Cube, arXiv:1307.1062.Google Scholar
Füredi, Z. and Simonovits, M. (2013) The history of the degenerate (bipartite) extremal graph problems. Erdős centennial, Bolyai Soc. Math. Stud. 25 169–264. JÁnos Bolyai Math. Soc., Budapest, 2013. See also arXiv:1306.5167.10.1007/978-3-642-39286-3_7CrossRefGoogle Scholar
Janzer, O. (2020) The extremal number of the subdivisions of the complete bipartite graph. SIAM J. Discrete Math. 34 241–250.10.1137/19M1269798CrossRefGoogle Scholar
Janzer, O. (2021) On the extremal number of longer subdivisions. Bull. Lond. Math. Soc. 53 108–118.10.1112/blms.12404CrossRefGoogle Scholar
Jiang, T., Jiang, Z. and Ma, J. Negligible Obstructions and Turán Exponents, arXiv:2007.02975.Google Scholar
Jiang, T. and Newman, A. (2017) Small dense subgraphs of a graph. SIAM J. Discrete Math. 31 124–142.10.1137/15M1007598CrossRefGoogle Scholar
Jiang, T. and Qiu, Y. (2020) Turán numbers of bipartite subdivisions. SIAM J. Discrete Math. 34 556–570.10.1137/19M1265442CrossRefGoogle Scholar
Jiang, T. and Qiu, Y. Many Turán exponents via subdivisions, arXiv:1908.02385.Google Scholar
Jiang, T. and Yepremyan, L. (2020) Supersaturation of even linear cycles in linear hypergraphs, Comb. Prob. Comp. 29 698–721.10.1017/S0963548320000206CrossRefGoogle Scholar
Kang, D.Y., Kim, J. and Liu, H. (2021) On the Turán exponents conjecture. J. Combin. Theory Ser B. 148 149–172.10.1016/j.jctb.2020.12.003CrossRefGoogle Scholar
Kollár, J., Rónyai, L. and Szabó, T. (1996) Norm-graphs and bipartite Turán numbers. Combinatorica 16 399–406.10.1007/BF01261323CrossRefGoogle Scholar
KövÁri, T., Sós, V. T. and Turán, P. (1954) On a problem of K. Zarankiewicz. Colloq. Math. 3 50–57.Google Scholar
Naor, A. and Verstraëte, J. (2005) A note on bipartite graphs without 2k-cycles. Comb. Prob. Comp. 14 845–849.10.1017/S0963548305007029CrossRefGoogle Scholar
Pinchasi, R. and Sharir, M. (2005) On graphs that do not contain the cube and related problems. Combinatorica 25 615–623.CrossRefGoogle Scholar