Hostname: page-component-cb9f654ff-rkzlw Total loading time: 0 Render date: 2025-08-06T12:37:17.530Z Has data issue: false hasContentIssue false
  • English
  • Français

On deficiency problems for graphs

Part of: Graph theory

Published online by Cambridge University Press:  27 September 2021

Andrea Freschi ,
Joseph Hyde  and
Andrew Treglown
Andrea Freschi
Affiliation:
School of Mathematics, University of Birmingham, Birmingham, B15 2TT, UK
Joseph Hyde
Affiliation:
Mathematics Institute, Zeeman Building, University of Warwick, Coventry CV4 7AL, UK
Andrew Treglown*
Affiliation:
School of Mathematics, University of Birmingham, Birmingham, B15 2TT, UK
*
*Corresponding author. Email: a.c.treglown@bham.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by analogous questions in the setting of Steiner triple systems and Latin squares, Nenadov, Sudakov and Wagner [Completion and deficiency problems, Journal of Combinatorial Theory Series B, 2020] recently introduced the notion of graph deficiency. Given a global spanning property 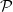$\mathcal P$ and a graph 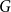$G$, the deficiency 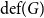$\text{def}(G)$ of the graph 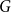$G$ with respect to the property 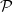$\mathcal P$ is the smallest non-negative integer t such that the join 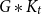$G*K_t$ has property 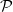$\mathcal P$. In particular, Nenadov, Sudakov and Wagner raised the question of determining how many edges an n-vertex graph 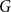$G$ needs to ensure 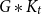$G*K_t$ contains a 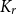$K_r$-factor (for any fixed 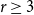$r\geq 3$). In this paper, we resolve their problem fully. We also give an analogous result that forces 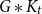$G*K_t$ to contain any fixed bipartite 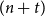$(n+t)$-vertex graph of bounded degree and small bandwidth.

Keywords

graph deficiencyclique factorsbandwidth theorems

MSC classification

Primary: 05C35: Extremal problems 05C70: Factorization, matching, partitioning, covering and packing 05C78: Graph labelling (graceful graphs, bandwidth, etc.)

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 3 , May 2022 , pp. 478 - 488
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Akiyama, A. and Frankl, P. (1985) On the size of graphs with complete-factors. J. Graph Theory 9 197–201.CrossRefGoogle Scholar
Böttcher, J., Schacht, M. and Taraz, A. (2009) Proof of the bandwidth conjecture of Bollobás and Komlós. Math. Ann. 343 175–205.CrossRefGoogle Scholar
Bryant, D. and Horsley, D. (2009) A proof of Lindner’s conjecture on embeddings of partial Steiner triple systems. J. Combin. Des. 17 63–89.CrossRefGoogle Scholar
Chvátal, V. (1972) On Hamilton’s ideals. J. Combin. Theory Ser. B 12 163–168.CrossRefGoogle Scholar
Daykin, D. and Häggkvist, R. (1983) Completion of sparse partial Latin square. In Proc. Cambridge Conference in Honour of Paul Erdös.Google Scholar
Evans, T. (1960) Embedding in complete Latin squares. Am. Math. Mon. 67 958–961.CrossRefGoogle Scholar
Füredi, Z. and Lehel, J. (2010) Tight embeddings of partial quadrilateral packings. J. Combin. Theory Ser. A 117 466–474.CrossRefGoogle Scholar
Füredi, Z., Riet, A. and Tyomkyn, M. (2011) Completing partial packings of bipartite graphs. J. Combin. Theory Ser. A 118 2463–2473.CrossRefGoogle Scholar
Hajnal, A. and Szemerédi, E. (1970) Proof of a conjecture of Erdős. Comb. Theory Appl vol. II 4 601–623.Google Scholar
Knox, F. and Treglown, A. (2013) Embedding spanning bipartite graphs of small bandwidth. Combin. Probab. Comput. 22 71–96.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2009) The minimum degree threshold for perfect graph packings. Combinatorica 29 65–107.CrossRefGoogle Scholar
Lindner, C. C. (1975) A partial Steiner triple system of order n can be embedded in a Steiner triple system of order $6n + 3$ . J. Combin. Theory Ser. A 18 349–351.CrossRefGoogle Scholar
Nenadov, R., Sudakov, B. and Wagner, A. Z. (2020) Completion and deficiency problems. J. Combin. Theory Ser. B 145 214–240.CrossRefGoogle Scholar