Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-12T13:06:04.409Z Has data issue: false hasContentIssue false
  • English
  • Français

Many Turán exponents via subdivisions

Part of: Graph theory

Published online by Cambridge University Press:  21 July 2022

Tao Jiang  and
Yu Qiu
Tao Jiang*
Affiliation:
Department of Mathematics, Miami University, Oxford, OH 45056, USA
Yu Qiu
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, Hefei, 230026, P.R. China
*
*Corresponding author. Email: jiangt@miamioh.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a graph 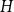$H$ and a positive integer $n$ , the Turán number 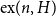$\mathrm{ex}(n,H)$ is the maximum number of edges in an $n$ -vertex graph that does not contain 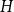$H$ as a subgraph. A real number 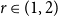$r\in (1,2)$ is called a Turán exponent if there exists a bipartite graph 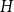$H$ such that 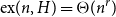$\mathrm{ex}(n,H)=\Theta (n^r)$ . A long-standing conjecture of Erdős and Simonovits states that 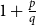$1+\frac{p}{q}$ is a Turán exponent for all positive integers 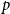$p$ and 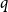$q$ with 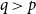$q\gt p$ .

In this paper, we show that 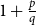$1+\frac{p}{q}$ is a Turán exponent for all positive integers 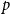$p$ and 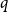$q$ with 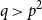$q \gt p^{2}$ . Our result also addresses a conjecture of Janzer [18].

Keywords

rational exponent conjectureTurán numberssubdivisions

MSC classification

Primary: 05C35: Extremal problems
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 32 , Issue 1 , January 2023 , pp. 134 - 150
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported in part by NSF grant DMS-1855542.

‡

Research supported in part by China Scholarship Council grant #201806340156.

References

Alon, N., Krivelevich, M. and Sudakov, B. (2003) Turán numbers of bipartite graphs and related Ramsey-type questions. Combin. Probab. Comput. 12(5-6) 477–494.CrossRefGoogle Scholar
Bukh, B. (2015) Random algebraic construction of extremal graphs. Bull. Lond. Math. Soc. 47(6) 939–945.Google Scholar
Bukh, B. and Conlon, D. (2018) Rational exponents in extremal graph theory. J. Eur. Math. Soc. 20 1747–1757.CrossRefGoogle Scholar
Brown, W. G. (1966) On graphs that do not contain a Thomsen graph. Can. Math. Bull. 9(3) 281–285.CrossRefGoogle Scholar
Conlon, D. (2019) Graphs with few paths of prescribed length between any two vertices. Bull. Lond. Math. Soc. 51(6) 1015–1021.CrossRefGoogle Scholar
Conlon, D. and Lee, J. (2021) On the extremal number of subdivisions. Int. Math. Res. Not. 2021(12) 9122–9145.CrossRefGoogle Scholar
Conlon, D., Janzer, O. and Lee, J. (2021) More on the extremal number of subdivisions. Combinatorica 411 465–494.CrossRefGoogle Scholar
Erdős, P. (1986) Problems and results in combinatorial analysis and graph theory. Proc. First Jpn. Conf. Graph Theory Appl. (Hakone) 72(1988) 81–92.Google Scholar
Erdös, P. and Stone, A. H. (1946) On the structure of linear graphs. Bull. Am. Math. Soc 52(12) 1087–1091.CrossRefGoogle Scholar
Erdős, P. and Simonovits, M. (1966) A limit theorem in graph theory. Studia Sci. Math. Hungar. 1 51–57.Google Scholar
Erdős, P. and Simonovits, M. (1970) Some extremal problems in graph theory. Comb. Theory Appl. (Proc. Colloq. Balatonfüred 1969) 1 370–390.Google Scholar
Erdős, P. and Stone, H. (1946) On the structure of linear graphs. Bull. Am. Math. Soc. 52 1087–1091.CrossRefGoogle Scholar
Faudree, R. and Simonovits, M. (1983) On a class of degenerate extremal graph problems. Combinatorica 3 83–93.CrossRefGoogle Scholar
Frankl, P. (1986) All rationals occur as exponents. J. Combin. Theory Ser. A 42 200–206.CrossRefGoogle Scholar
Füredi, Z. (1991) On a Turán type problem of Erdős. Combinatorica 11 75–79.CrossRefGoogle Scholar
Füredi, Z. and Simonovits, M. (2013) The history of the degenerate (bipartite) extremal graph problems. Erdős centennial, Bolyai Soc. Math. Stud. 25 169–264, János Bolyai Math. Soc., Budapest, 2013. See also arXiv:1306.5167.CrossRefGoogle Scholar
Janzer, O. (2019) Improved bounds for the extremal number of subdivisions. Electron. J. Comb. 26(3) P3.3.CrossRefGoogle Scholar
Janzer, O. (2020) The extremal number of the subdivisions of the complete bipartite graph. SIAM J. Discrete Math. 34(1) 241–250.CrossRefGoogle Scholar
Janzer, O. (2021) The extremal number of longer subdivisions. Bull. London Math. Soc. 53(1) 108–118.CrossRefGoogle Scholar
Jiang, T. (2011) Compact topological minors in graphs. J. Graph Theory 67(2) 139–152.CrossRefGoogle Scholar
Jiang, T., Ma, J. and Yepremyan, L. (2022) On Turán exponents of bipartite graphs. Combin. Probab. Comput. 31(2) 333–344.CrossRefGoogle Scholar
Jiang, T. and Qiu, Y. (2020) Turán numbers of bipartite subdivisions. SIAM J. Discrete Math. 34(1) 556–570.CrossRefGoogle Scholar
Jiang, T. and Qiu, Y. () Many Turán exponents via subdivisions, arXiv:1908.02385v1,CrossRefGoogle Scholar
Jiang, T. and Seiver, R. (2012) Turán numbers of subdivided graphs. SIAM J. Discrete Math 26(3) 1238–1255.CrossRefGoogle Scholar
Kang, D. Y., Kim, J. and Liu, H. (2021) On the rational Turán exponent conjecture. J. Combin. Theory Ser. B 148 149–172.CrossRefGoogle Scholar
Kővári, T., Sós, V. T. and Turán, P. (1954) On a problem of K Zarankiewicz. Colloq. Math. 3(1) 50–57.CrossRefGoogle Scholar