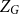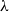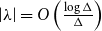Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Liu, Jingcheng
Wang, Chunyang
Yin, Yitong
and
Yu, Yixiao
2025.
Phase Transitions via Complex Extensions of Markov Chains.
p.
903.