Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-11T09:59:46.517Z Has data issue: false hasContentIssue false
  • English
  • Français

A central limit theorem for additive functionals of increasing trees

Part of: Graph theory Limit theorems Combinatorial probability

Published online by Cambridge University Press:  08 March 2019

Dimbinaina Ralaivaosaona  and
Stephan Wagner
Dimbinaina Ralaivaosaona
Affiliation:
Department of Mathematical Sciences, Stellenbosch University, 7602 Stellenbosch, South Africa
Stephan Wagner*
Affiliation:
Department of Mathematical Sciences, Stellenbosch University, 7602 Stellenbosch, South Africa
*
*Corresponding author. Email: swagner@sun.ac.za
Get access Rights & Permissions [Opens in a new window]

Abstract

A tree functional is called additive if it satisfies a recursion of the form 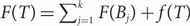$F(T) = \sum_{j=1}^k F(B_j) + f(T)$, where B1, …, Bk are the branches of the tree T and f (T) is a toll function. We prove a general central limit theorem for additive functionals of d-ary increasing trees under suitable assumptions on the toll function. The same method also applies to generalized plane-oriented increasing trees (GPORTs). One of our main applications is a log-normal law that we prove for the size of the automorphism group of d-ary increasing trees, but other examples (old and new) are covered as well.

MSC classification

Primary: 60C05: Combinatorial probability
Secondary: 05C05: Trees 60F05: Central limit and other weak theorems
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 28 , Special Issue 4: Analysis of Algorithms , July 2019 , pp. 618 - 637
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

An extended abstract of this paper was presented at the 27th International Conference on Probabilistic, Combinatorial and Asymptotic Methods for the Analysis of Algorithms, Kraków, 4–8 July 2016: see [15].

§

Supported by the Division for Research Development (DRD) of Stellenbosch University.

This material is based upon work supported by the National Research Foundation under grant number 96236.

References

Bergeron, F., Flajolet, P. and Salvy, B. (1992) Varieties of increasing trees. In Colloquium on Trees in Algebra and Programming (CAAP ’92), Vol. 581 of Lecture Notes in Computer Science, Springer, pp. 24–48.CrossRefGoogle Scholar
Bóna, M. and Flajolet, P. (2009) Isomorphism and symmetries in random phylogenetic trees. J. Appl. Probab. 46 1005–1019.CrossRefGoogle Scholar
Devroye, L. (2002/03) Limit laws for sums of functions of subtrees of random binary search trees. SIAM J. Comput. 32 152–171.CrossRefGoogle Scholar
Drmota, M. (2009) Random Trees: An Interplay Between Combinatorics and Probability, Springer.CrossRefGoogle Scholar
Fill, J. A., Flajolet, P. and Kapur, N. (2005) Singularity analysis, Hadamard products, and tree recurrences. J. Comput. Appl. Math. 174 271–313.CrossRefGoogle Scholar
Fill, J. A. and Kapur, N. (2004) Limiting distributions for additive functionals on Catalan trees. Theoret. Comput. Sci. 326 69–102.CrossRefGoogle Scholar
Flajolet, P. and Sedgewick, R. (2009) Analytic Combinatorics, Cambridge University Press.CrossRefGoogle Scholar
Fuchs, M. (2012) Limit theorems for subtree size profiles of increasing trees. Combin. Probab. Comput. 21 412–441.CrossRefGoogle Scholar
Holmgren, C. and Janson, S. (2015) Limit laws for functions of fringe trees for binary search trees and random recursive trees. Electron. J. Probab. 20 #4.CrossRefGoogle Scholar
Holmgren, C., Janson, S. and Šileikis, M. (2017) Multivariate normal limit laws for the numbers of fringe subtrees in m-ary search trees and preferential attachment trees. Electron. J. Combin. 24 P2.51.Google Scholar
Hwang, H.-K. and Neininger, R. (2002) Phase change of limit laws in the quicksort recurrence under varying toll functions. SIAM J. Comput. 31 1687–1722.CrossRefGoogle Scholar
Janson, S. (2016) Asymptotic normality of fringe subtrees and additive functionals in conditioned Galton–Watson trees. Random Struct. Alg. 48 57–101.CrossRefGoogle Scholar
Meir, A. and Moon, J. W. (1998) On the log-product of the subtree-sizes of random trees. Random Struct. Alg. 12 197–212.3.0.CO;2-S>CrossRefGoogle Scholar
Panholzer, A. and Prodinger, H. (2007) Level of nodes in increasing trees revisited. Random Struct. Alg. 31 203–226.CrossRefGoogle Scholar
Ralaivaosaona, D. and Wagner, S. (2016) Additive functionals of d-ary increasing trees. In Proceedings of the 27th International Conference on Probabilistic, Combinatorial and Asymptotic Methods for the Analysis of Algorithms. arXiv:1605.03918Google Scholar
Semple, C. and Steel, M. (2003) Phylogenetics, Oxford University Press.Google Scholar
Wagner, S. (2015) Central limit theorems for additive tree parameters with small toll functions. Combin. Probab. Comput. 24 329–353.CrossRefGoogle Scholar