Article contents
Powers of paths in tournaments
Published online by Cambridge University Press: 23 March 2021
Abstract
In this short note we prove that every tournament contains the k-th power of a directed path of linear length. This improves upon recent results of Yuster and of Girão. We also give a complete solution for this problem when k=2, showing that there is always a square of a directed path of length 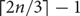 , which is best possible.
, which is best possible.
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
Footnotes
Research supported in part by SNSF grant 200021_196965
Research supported in part by ERC grant No 714704
Research supported by a Packard Fellowship and by NSF award DMS-185563.
Research supported by DFG under Germany’s Excellence Strategy EXC-2181/1 - 390900948.
Research supported in part by Agence Nationale de la Recherche under contract Digraphs ANR-19-CE48-0013-01.
Supported by SNSF Postdoc.Mobility Fellowship P400P2_186686.
Research supported by ERC grant No 819416.
References
- 7
- Cited by


