Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Pach, János
Suk, Andrew
and
Treml, Miroslav
2010.
Tangencies between families of disjoint regions in the plane.
p.
423.
Pach, János
Suk, Andrew
and
Treml, Miroslav
2012.
Tangencies between families of disjoint regions in the plane.
Computational Geometry,
Vol. 45,
Issue. 3,
p.
131.


 are families of plane convex sets with
are families of plane convex sets with  for some
for some 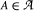 touches every
touches every 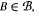 then either
then either 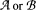 contains
contains 