No CrossRef data available.
Article contents
On Density of Generalized Polynomials
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We consider the density in C[a, b] of generalized polynomials of the form 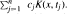 The main point of this note is that total positivity of K(x, t) has little relationship to density: There is a symmetric, analytic, totally positive (in fact ETP (∞)) kernel K for which these generalized polynomials are not dense.
The main point of this note is that total positivity of K(x, t) has little relationship to density: There is a symmetric, analytic, totally positive (in fact ETP (∞)) kernel K for which these generalized polynomials are not dense.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1991
References
1.
Achiezer, N. I., Theory of Approximation, (transi, by C. J. Hyman), Ungar, New York, 1956.Google Scholar
2.
Dyn, N. and Lubinsky, D. S., Convergence of Interpolation to Transforms of Totally Positive Kernels, Can. J. Math., 40 (1988), 750–768.Google Scholar
3.
Gierz, G. and Shekhtman, B., A Duality Principle for Rational Approximation, Pacific J. Math., 125 (1986), 79–92.Google Scholar
4.
Gierz, G. and Shekhtman, B., On Spaces with Large Chebyshev Subspaces, J. Approx. Th., 54 (1988), 155— 161.Google Scholar
5.
Karlin, S., The Existence of Eigenvalues for Integral Operators, Trans. Amer. Math. Soc, 113 (1964), 1–17.Google Scholar
6.
Karlin, S., Total positivity and convexity preserving transformations, Proc. Sympos. Pure Math., 7 (1963), 329–347.Google Scholar

