Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
1985.
Ergodic Theorems.
p.
321.
Tempelman, Arkady
1992.
Ergodic Theorems for Group Actions.
p.
207.
Argiris, Georgios
and
Rosenblatt, Joseph M.
2006.
Forcing Divergence When the Supremum Is Not Integrable.
Positivity,
Vol. 10,
Issue. 2,
p.
261.

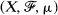 be a σ-finite measure space, {T
be a σ-finite measure space, {T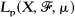 , some p, 1≤p≤∞.If
, some p, 1≤p≤∞.If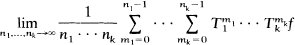
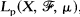 , p fixed, 1<p<∞, then the multiple sequence ergodic theorem holds for {T
, p fixed, 1<p<∞, then the multiple sequence ergodic theorem holds for {T