Hostname: page-component-f554764f5-246sw Total loading time: 0 Render date: 2025-04-10T04:16:25.757Z Has data issue: false hasContentIssue false
  • English
  • Français

Matrix inequalities and majorizations around Hermite–Hadamard’s inequality

Part of: Basic linear algebra General theory of linear operators

Published online by Cambridge University Press:  10 January 2022

Jean-Christophe Bourin  and
Eun-Young Lee
Jean-Christophe Bourin*
Affiliation:
Laboratoire de mathématiques, Université de Bourgogne Franche-Comté, 25000, Besançon, France
Eun-Young Lee
Affiliation:
Department of mathematics, KNU-Center for Nonlinear Dynamics, Kyungpook National University, 702-701, Daegu, Korea e-mail: eylee89@knu.ac.kr
*
e-mail: jcbourin@univ-fcomte.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the classical Hermite–Hadamard inequality in the matrix setting. This leads to a number of interesting matrix inequalities such as the Schatten p-norm estimates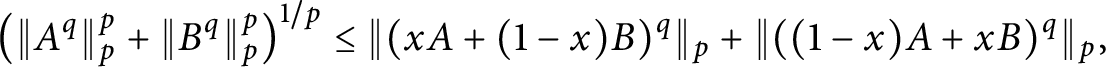

$$ \begin{align*}\left(\|A^q\|_p^p + \|B^q\|_p^p\right)^{1/p} \le \|(xA+(1-x)B)^q\|_p+ \|((1-x)A+xB)^q\|_p, \end{align*} $$
for all positive (semidefinite) $n\times n$ matrices 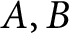$A,B$ and 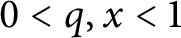$0<q,x<1$ . A related decomposition, with the assumption 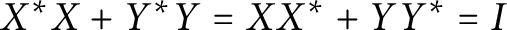$X^*X+Y^*Y=XX^*+YY^*=I$ , is
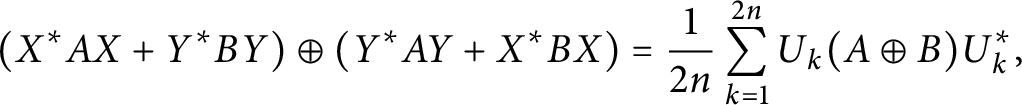$$ \begin{align*}(X^*AX+Y^*BY)\oplus (Y^*AY+X^*BX) =\frac{1}{2n}\sum_{k=1}^{2n} U_k (A\oplus B)U_k^*, \end{align*} $$
for some family of $2n\times 2n$ unitary matrices $U_k$ . This is a majorization which is obtained by using the Hansen–Pedersen trace inequality.

Keywords

Positive definite matricesblock matricesconvex functionsmatrix inequalities

MSC classification

Primary: 15A45: Miscellaneous inequalities involving matrices 47A60: Functional calculus
Secondary: 15A60: Norms of matrices, numerical range, applications of functional analysis to matrix theory 47A30: Norms (inequalities, more than one norm, etc.)
Type
Article
Information
Canadian Mathematical Bulletin , Volume 65 , Issue 4 , December 2022 , pp. 943 - 952
Check for updates
Copyright
© Canadian Mathematical Society, 2022

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

J.-C. Bourin was funded by the ANR Projet (No. ANR-19-CE40-0002) and by the French Investissements d’Avenir program, project ISITE-BFC (contract ANR-15-IDEX-03). This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2018R1D1A3B07043682).

References

Ando, T., Majorization, doubly stochastic matrices, and comparison of eigenvalues. Linear Algebra Appl. 118(1989), 163–248.Google Scholar
Bhatia, R., Matrix analysis. Vol. 169, Graduate Texts in Mathematics, Springer, New York, 1996.Google Scholar
Bhatia, R., Positive definite matrices. Princeton University Press, Princeton, NJ, 2007.Google Scholar
Bourin, J.-C. and Hiai, F., Norm and anti-norm inequalities for positive semi-definite matrices. Internat. J. Math. 22(2011), no. 8, 1121–1138.CrossRefGoogle Scholar
Bourin, J.-C. and Hiai, F., Jensen and Minkowski inequalities for operator means and anti-norms. Linear Algebra Appl. 456(2014), 22–53.CrossRefGoogle Scholar
Bourin, J.-C. and Lee, E.-Y., Unitary orbits of Hermitian operators with convex or concave functions. Bull. Lond. Math. Soc. 44(2012), no. 6, 1085–1102.CrossRefGoogle Scholar
Bourin, J.-C. and Lee, E.-Y., A Pythagorean theorem for partitioned matrices. Proc. Amer. Math. Soc., in press.Google Scholar
Hansen, F. and Pedersen, G. K., Jensen’s operator inequality. Bull. Lond. Math. Soc. 35(2003), no. 4, 553–564.CrossRefGoogle Scholar
Hiai, F., Matrix analysis: matrix monotone functions, matrix means, and majorization. Interdiscip. Inform. Sci. 16(2010), no. 2, 139–248.Google Scholar
Hiai, F. and Petz, D., Introduction to matrix analysis and applications. Universitext, Springer, Cham; Hindustan Book Agency, New Delhi, 2014.CrossRefGoogle Scholar
Moslehian, M. S., Matrix Hermite–Hadamard type inequalities. Houston J. Math. 39(2013), no. 1, 177–189.Google Scholar
Niculescu, C. P. and Persson, L.-E., Old and new on the Hermite–Hadamard inequality. Real Anal. Exchange 29(2004), no. 2, 663–685.Google Scholar
Simon, B., Trace ideals and their applications. 2nd ed., Mathematical Surveys and Monographs, 120, American Mathematical Society, Providence, RI, 2005.Google Scholar
Zhan, X., The sharp Rado theorem for majorizations. Amer. Math. Monthly 110(2003), 152–153.Google Scholar