No CrossRef data available.
Article contents
James-Hopf Invariants, Anick’s Spaces, and the Double Loops on Odd Primary Moore Spaces
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Using spaces introduced by Anick, we construct a decomposition into indecomposable factors of the double loop spaces of odd primary Moore spaces when the powers of the primes are greater than the first power. If  $n$ is greater than 1, this implies that the odd primary part of all the homotopy groups of the
$n$ is greater than 1, this implies that the odd primary part of all the homotopy groups of the 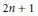 $2n\,+\,1$ dimensional sphere lifts to a mod
$2n\,+\,1$ dimensional sphere lifts to a mod 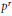 ${{p}^{r}}$ Moore space.
${{p}^{r}}$ Moore space.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2000
References
[1]
Anick, D., Differential Algebras in Topology. Res. Notes Math. 3, A.K. Peters Ltd., 1993.Google Scholar
[2]
Anick, D. and Gray, B., Small H spaces related to Moore spaces. Topology 43(1995), 859–881.Google Scholar
[3]
Cohen, F. R. and Mahowald, M. E., A remark on self-maps of Ω2S2n+1
. Indiana Univ. Math J. 30(1981), 583–588.Google Scholar
[4]
Cohen, F. R., Moore, J. C. and Neisendorfer, J. A., Torsion in homotopy groups. Ann. of Math. 109(1979), 121–168.Google Scholar
[5]
Cohen, F. R., Moore, J. C. and Neisendorfer, J. A., The double suspension and exponents of the homotopy groups of spheres. Ann. of Math. 110(1979), 549–565.Google Scholar
[6]
Cohen, F. R., Moore, J. C. and Neisendorfer, J. A., Exponents in homotopy theory. In: Algebraic Topology and Algebraic K-theory (ed. Browder, W.), Princeton Univ. Press, 1987.Google Scholar
[9]
Neisendorfer, J. A., Properties of certain H-spaces. Quart. Math, J..Oxford Ser. (2) 34(1983), 201–209.Google Scholar
[10]
Neisendorfer, J. A., The exponent of a Moore space. In: Algebraic Topology and Algebraic K-theory (ed. Browder, W.), Princeton Univ. Press, 1987.Google Scholar
[11]
Neisendorfer, J. A., Product decompositions of the double loops on odd primary Moore spaces. Topology, to appear.Google Scholar
[13]
Theriault, S. D., A reconstruction of Anick's fibration, University of Toronto Thesis, 1997.Google Scholar

