Article contents
A Generalization of a Theorem of Hilton
Published online by Cambridge University Press: 20 November 2018
Extract
Let f: A×B → X be a map. Let J(f): ∑(A ∧ B)→ ∑X be the map obtained from f by means of the Hopf construction. Let P(f) denote the space obtained from ∑X by attaching a cone on ∑(A ∧ B) by means of J(f). Let l: ∑X→P(f ) be the inclusion and T(l): X→ΩP(f) the adjoint of l. Let h1,: A1, → A, h2: B1,→ B be maps. Let c:ΩP(f)× ΩP(f) → ΩP(f) be the basic commutator. Then we prove that there exists a map ∑A1 × ∑B1 →P(f) with axes l∑(fi1 h1), l∑(fi2 h2) if and only if 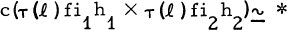 , where i1: A→ A × B and i2 B → A × B are the inclusions. This generalizes a result of Hilton. Also, by letting f be an H-space multiplication and h and h the identity maps, we obtain a well known criterion of Stasheff for an H-space to be homotopy-commutative. Finally, appropriate duals of these results are given.
, where i1: A→ A × B and i2 B → A × B are the inclusions. This generalizes a result of Hilton. Also, by letting f be an H-space multiplication and h and h the identity maps, we obtain a well known criterion of Stasheff for an H-space to be homotopy-commutative. Finally, appropriate duals of these results are given.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1968
References
- 1
- Cited by

