No CrossRef data available.
Article contents
Factorization Tests and Algorithms Arising from Counting Modular Forms and Automorphic Representations
Published online by Cambridge University Press: 09 January 2019
Abstract
A theorem of Gekeler compares the number of non-isomorphic automorphic representations associated with the space of cusp forms of weight 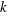 $k$ on
$k$ on 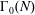 $\unicode[STIX]{x0393}_{0}(N)$ to a simpler function of
$\unicode[STIX]{x0393}_{0}(N)$ to a simpler function of 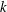 $k$ and
$k$ and 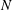 $N$, showing that the two are equal whenever
$N$, showing that the two are equal whenever 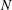 $N$ is squarefree. We prove the converse of this theorem (with one small exception), thus providing a characterization of squarefree integers. We also establish a similar characterization of prime numbers in terms of the number of Hecke newforms of weight
$N$ is squarefree. We prove the converse of this theorem (with one small exception), thus providing a characterization of squarefree integers. We also establish a similar characterization of prime numbers in terms of the number of Hecke newforms of weight 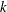 $k$ on
$k$ on 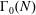 $\unicode[STIX]{x0393}_{0}(N)$.
$\unicode[STIX]{x0393}_{0}(N)$.
It follows that a hypothetical fast algorithm for computing the number of such automorphic representations for even a single weight 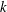 $k$ would yield a fast test for whether
$k$ would yield a fast test for whether 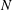 $N$ is squarefree. We also show how to obtain bounds on the possible square divisors of a number
$N$ is squarefree. We also show how to obtain bounds on the possible square divisors of a number 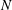 $N$ that has been found not to be squarefree via this test, and we show how to probabilistically obtain the complete factorization of the squarefull part of
$N$ that has been found not to be squarefree via this test, and we show how to probabilistically obtain the complete factorization of the squarefull part of 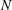 $N$ from the number of such automorphic representations for two different weights. If in addition we have the number of such Hecke newforms for even a single weight
$N$ from the number of such automorphic representations for two different weights. If in addition we have the number of such Hecke newforms for even a single weight 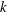 $k$, then we show how to probabilistically factor
$k$, then we show how to probabilistically factor 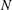 $N$ entirely. All of these computations could be performed quickly in practice, given the number(s) of automorphic representations and modular forms as input.
$N$ entirely. All of these computations could be performed quickly in practice, given the number(s) of automorphic representations and modular forms as input.
Keywords
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
Footnotes
The second author’s work is partially supported by a National Sciences and Engineering Research Council of Canada Discovery Grant.

