No CrossRef data available.
Published online by Cambridge University Press: 24 May 2022
We establish a theory of noncommutative (NC) functions on a class of von Neumann algebras with a particular direct sum property, e.g.,
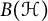 $B({\mathcal H})$
. In contrast to the theory’s origins, we do not rely on appealing to results from the matricial case. We prove that the
$B({\mathcal H})$
. In contrast to the theory’s origins, we do not rely on appealing to results from the matricial case. We prove that the
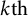 $k{\mathrm {th}}$
directional derivative of any NC function at a scalar point is a k-linear homogeneous polynomial in its directions. Consequences include the fact that NC functions defined on domains containing scalar points can be uniformly approximated by free polynomials as well as realization formulas for NC functions bounded on particular sets, e.g., the NC polydisk and NC row ball.
$k{\mathrm {th}}$
directional derivative of any NC function at a scalar point is a k-linear homogeneous polynomial in its directions. Consequences include the fact that NC functions defined on domains containing scalar points can be uniformly approximated by free polynomials as well as realization formulas for NC functions bounded on particular sets, e.g., the NC polydisk and NC row ball.
This research was partially supported by the National Science Foundation Grant DMS 2054199.