Contents
Research Article
A New Type of Characteristic Subgroup of Prime-Power Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 477-482
-
- Article
-
- You have access
- Export citation
A Theorem on Pure Submodules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 483-487
-
- Article
-
- You have access
- Export citation
Nodal Non-Commutative Jordan Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 488-492
-
- Article
-
- You have access
- Export citation
Generalized Lie Elements
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 493-502
-
- Article
-
- You have access
- Export citation
Modifications and Cobounding Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 503-528
-
- Article
-
- You have access
- Export citation
On Immersion of Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 529-534
-
- Article
-
- You have access
- Export citation
The Enumeration of Point Labelled Chromatic Graphs and Trees
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 535-545
-
- Article
-
- You have access
- Export citation
Some Generalized Theorems on Connectivity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 546-554
-
- Article
-
- You have access
- Export citation
On Orientations, Connectivity and Odd-Vertex-Pairings in Finite Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 555-567
-
- Article
-
- You have access
- Export citation
On the Projective Centres of Convex Curves
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 568-581
-
- Article
-
- You have access
- Export citation
A Semimodular Imbedding of Lattices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 582-591
-
- Article
-
- You have access
- Export citation
Intersection Irreducible Ideals of a Non-Commutative Principal Ideal Domain
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 592-596
-
- Article
-
- You have access
- Export citation
On Continuous Regular Rings and Semisimple Self Injective Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 597-605
-
- Article
-
- You have access
- Export citation
Automorphisms of Finite Linear Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 606-615
-
- Article
-
- You have access
- Export citation
Invariants of Finite Reflection Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 616-618
-
- Article
-
- You have access
- Export citation
A Metrical Theorem in Diophantine Approximation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 619-631
-
- Article
-
- You have access
- Export citation
A Local Property of Measurable Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 632-640
-
- Article
-
- You have access
- Export citation
On a Class of Non-Self-Adjoint Differential Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 641-659
-
- Article
-
- You have access
- Export citation
The Gibbs Phenomenon for Taylor Means and for [F, Dn] Means
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 660-673
-
- Article
-
- You have access
- Export citation
Continuous Translation of Hölder and Lipschitz Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 674-685
-
- Article
-
- You have access
- Export citation
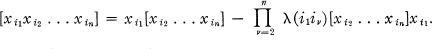

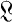 often can be facilitated by imbedding
often can be facilitated by imbedding  of a more restricted type whose properties are known. However, if
of a more restricted type whose properties are known. However, if