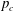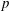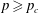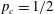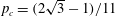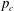Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 13
Genus 2 Curves with Quaternionic Multiplication
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 734-757
-
- Article
-
- You have access
- Export citation
- Cited by 13
On the Sum of the Reciprocals of the Fermat Numbers and Related Irrationalities
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 475-478
-
- Article
-
- You have access
- Export citation
- Cited by 13
Consistency of Moment Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 995-1006
-
- Article
-
- You have access
- Export citation
- Cited by 13
Cohomology of Complex Projective Stiefel Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 897-914
-
- Article
-
- You have access
- Export citation
- Cited by 13
Tensor Products of Analytic Continuations of Holomorphic Discrete Series
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1224-1241
-
- Article
-
- You have access
- Export citation
- Cited by 13
Bireflectionality in Classical Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1157-1162
-
- Article
-
- You have access
- Export citation
- Cited by 13
Subgroups of the Power Semigroup of a Finite Semigroup
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1077-1083
-
- Article
-
- You have access
- Export citation
- Cited by 13
On Bernstein's Inequality
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 347-353
-
- Article
-
- You have access
- Export citation
- Cited by 13
The Pexider Functional Equations in Distributions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 304-314
-
- Article
-
- You have access
- Export citation
- Cited by 13
Right-Ordered Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 891-895
-
- Article
-
- You have access
- Export citation
- Cited by 13
On a Conjecture of Chowla and Milnor
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1328-1344
-
- Article
-
- You have access
- Export citation
- Cited by 13
Antichains and Finite Sets that Meet all Maximal Chains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 619-632
-
- Article
-
- You have access
- Export citation
- Cited by 13
Minimal Rates of Summability
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 808-816
-
- Article
-
- You have access
- Export citation
- Cited by 13
An Extremum Result
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 597-601
-
- Article
-
- You have access
- Export citation
- Cited by 13
A Boltzmann Approach to Percolation on Random Triangulations
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2019, pp. 1-43
-
- Article
-
- You have access
- Export citation
- Cited by 12
On Lie Semi-Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 686-693
-
- Article
-
- You have access
- Export citation
- Cited by 12
Transcendental Nature of Special Values of L-Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 136-152
-
- Article
-
- You have access
- Export citation
- Cited by 12
Local Topological Properties and One Point Extensions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 338-348
-
- Article
-
- You have access
- Export citation
- Cited by 12
Variation of constants formula and exponential dichotomy for nonautonomous non-densely defined Cauchy problems
- Part of:
-
- Published online by Cambridge University Press:
- 29 June 2020, pp. 1347-1389
-
- Article
- Export citation
- Cited by 12
Shimura Varieties and the Selberg Trace Formula
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1292-1299
-
- Article
-
- You have access
- Export citation





 , with μ a nonnegative measure. In associated optimization problems it is also important to be able to distinguish between the interior and boundary of the moment cone. Recent work of Dachuna-Castelle, Gamboa and Gassiat derived elegant computational characterizations for these problems, and for related questions with an upper bound on μ. Their technique involves a probabilistic interpretation and large deviations theory. In this paper a purely convex analytic approach is used, giving a more direct understanding of the underlying duality, and allowing the relaxation of their assumptions.
, with μ a nonnegative measure. In associated optimization problems it is also important to be able to distinguish between the interior and boundary of the moment cone. Recent work of Dachuna-Castelle, Gamboa and Gassiat derived elegant computational characterizations for these problems, and for related questions with an upper bound on μ. Their technique involves a probabilistic interpretation and large deviations theory. In this paper a purely convex analytic approach is used, giving a more direct understanding of the underlying duality, and allowing the relaxation of their assumptions.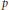
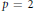
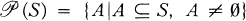 . If
. If 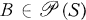 , then let
, then let 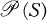 has been studied by many authors, including
has been studied by many authors, including 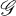 a subgroup of
a subgroup of 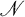 such that
such that 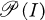 and
and  is isomorphic to a subgroup of
is isomorphic to a subgroup of 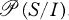 .
.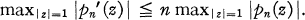
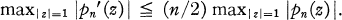
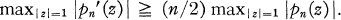
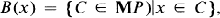
 .
.