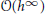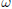Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 6
Integral Functions With Negative Zeros
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 179-184
-
- Article
-
- You have access
- Export citation
- Cited by 6
On Some Matrix Theoremsof Frobenius and McCoy
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 332-335
-
- Article
-
- You have access
- Export citation
- Cited by 6
Abstract Definitions for Reflection Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 273-276
-
- Article
-
- You have access
- Export citation
- Cited by 6
Some Formulas Involving Ramanujan Sums
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 284-286
-
- Article
-
- You have access
- Export citation
- Cited by 6
A Decomposition Theorem for Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 344-349
-
- Article
-
- You have access
- Export citation
- Cited by 6
Primary Ideals in Prüfer Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1024-1030
-
- Article
-
- You have access
- Export citation
- Cited by 6
Sums of Two Squares in Short Intervals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-694
-
- Article
-
- You have access
- Export citation
- Cited by 6
The 2-Sylow-Subgroup of the Tame Kernel of Number Fields
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 255-264
-
- Article
-
- You have access
- Export citation
- Cited by 6
Criteria for a Hadamard Matrix to be Skew-Equivalent
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1216-1223
-
- Article
-
- You have access
- Export citation
- Cited by 6
Convolution of Trace Class Operators over Locally Compact Quantum Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1043-1072
-
- Article
-
- You have access
- Export citation
- Cited by 6
The Local Product Structure of Expansive Automorphisms of Solenoids and Their Associated C*-Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 692-709
-
- Article
-
- You have access
- Export citation
- Cited by 6
Solvable Points on Projective Algebraic Curves
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 612-637
-
- Article
-
- You have access
- Export citation
- Cited by 6
Relative Kloosterman Integrals for GL(3): II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1220-1240
-
- Article
-
- You have access
- Export citation
- Cited by 6
Root Systems and Cartan Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 63-79
-
- Article
-
- You have access
- Export citation
- Cited by 6
Semi-Classical Behavior of the Scattering Amplitude for Trapping Perturbations at Fixed Energy
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 794-824
-
- Article
-
- You have access
- Export citation
- Cited by 6
Certain Integral Equalities which Imply Equimeasurability of Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 827-844
-
- Article
-
- You have access
- Export citation
- Cited by 6
Quasimap Floer Cohomology for Varying Symplectic Quotients
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 467-480
-
- Article
-
- You have access
- Export citation
- Cited by 6
Automorphisms of G-Azumaya Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1047-1058
-
- Article
-
- You have access
- Export citation
- Cited by 6
On Bounded and Compact Composition Operators in Polydiscs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 869-889
-
- Article
-
- You have access
- Export citation
- Cited by 6
The Addition of Primes and Power
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 512-526
-
- Article
-
- You have access
- Export citation
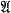 any algebra of n ⨯ n matrices over k which contains the identity I . Define a
any algebra of n ⨯ n matrices over k which contains the identity I . Define a 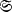 of
of 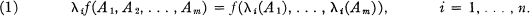
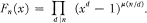
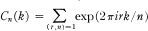
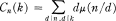



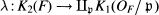 with a finite kernel, which is called the tame kernel, isomorphic to
with a finite kernel, which is called the tame kernel, isomorphic to 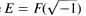 and
and  . A matrix
. A matrix  is of
is of  is
is  . A matrix P is a
. A matrix P is a 


















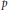
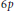
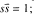 the group
the group