Contents
Research Article
Some Values for the Rogers-Ramanujan Continued Fraction
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 897-914
-
- Article
-
- You have access
- Export citation
Closed Ideals in a Convolution Algebra of Holomorphic Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 915-928
-
- Article
-
- You have access
- Export citation
Cliques of Irreducible Representations, Quotient Groups, and Brauer's Theorems on Blocks
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 929-945
-
- Article
-
- You have access
- Export citation
Extreme Measures with Given Moments or Marginals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 946-958
-
- Article
-
- You have access
- Export citation
A Bernstein-Schoenberg Type Operator: Shape Preserving and Limiting Behaviour
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 959-973
-
- Article
-
- You have access
- Export citation
On the Fundamental Lemma for Standard Endoscopy: Reduction to Unit Elements
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 974-994
-
- Article
-
- You have access
- Export citation
Consistency of Moment Systems
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 995-1006
-
- Article
-
- You have access
- Export citation
On Permutability and Submultiplicativity of Spectral Radius
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1007-1022
-
- Article
-
- You have access
- Export citation
Proof, Disproof and Advances Concerning Certain Conjectures on Real Quadratic Fields
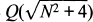
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1023-1036
-
- Article
-
- You have access
- Export citation
Residue Integrals and their Mellin Transforms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1037-1050
-
- Article
-
- You have access
- Export citation
Frames and Stable Bases for Shift-Invariant Subspaces of L2(ℝd)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1051-1094
-
- Article
-
- You have access
- Export citation
є-Families of Operators in Triebel-Lizorkin and Tent Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1095-1120
-
- Article
-
- You have access
- Export citation
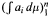 , with μ a nonnegative measure. In associated optimization problems it is also important to be able to distinguish between the interior and boundary of the moment cone. Recent work of Dachuna-Castelle, Gamboa and Gassiat derived elegant computational characterizations for these problems, and for related questions with an upper bound on μ. Their technique involves a probabilistic interpretation and large deviations theory. In this paper a purely convex analytic approach is used, giving a more direct understanding of the underlying duality, and allowing the relaxation of their assumptions.
, with μ a nonnegative measure. In associated optimization problems it is also important to be able to distinguish between the interior and boundary of the moment cone. Recent work of Dachuna-Castelle, Gamboa and Gassiat derived elegant computational characterizations for these problems, and for related questions with an upper bound on μ. Their technique involves a probabilistic interpretation and large deviations theory. In this paper a purely convex analytic approach is used, giving a more direct understanding of the underlying duality, and allowing the relaxation of their assumptions.