Hostname: page-component-7dd5485656-k8lnt Total loading time: 0 Render date: 2025-10-30T14:28:34.363Z Has data issue: false hasContentIssue false
  • English
  • Français

A Singular Boundary Value Problem for a Non-Self-Adjoint Differential Operator

Published online by Cambridge University Press:  20 November 2018

R. R. D. Kemp
R. R. D. Kemp*
Affiliation:
Queen's University Kingston
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

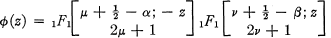If the differential expression l(y) = — y” + g(x)y generates a closed operator L on L2(— ∞, ∞), with domain D consisting of those functions y ∈ L2 with absolutely continuous derivatives and such that l(y) ∈ L2. The case where g(x) is real-valued has been extensively investigated and yields an expansion of any ƒ ∈ L2 in terms of the characteristic functions of L. We shall investigate the case where g is complex-valued.

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 10 , 1958 , pp. 447 - 462
Copyright
Copyright © Canadian Mathematical Society 1958 

Footnotes

This paper contains the results of the author's doctoral thesis at the Massachusetts Institute of Technology, with some corrections suggested by the referee. The author wishes to thank Professor Norman Levinson for his suggestion of the topic and his assistance thereafter. The final revision of this paper was carried out while the author was supported by a contract with the United States Air Force Office of Scientific Research.

References

1. Coddington, E. A. and Levinson, N., Theory of Ordinary Differential Equations (New York, 1955).Google Scholar
2. Naimark, M. A., Investigation of the spectrum and expansion in eigenfunctions of a non-self - adjoint differential operator of the second order on a semi-axis, Trudy Moskov Mat. Obsc, 3 (1954), 181–270.Google Scholar
3. Titchmarsh, E. C., Eigenf unction Expansions (Oxford, 1946).Google Scholar