Article contents
On the Cohomology of Moduli of Vector Bundles and the Tamagawa Number of SLn
Published online by Cambridge University Press: 20 November 2018
Abstract
We compute some Hodge and Betti numbers of the moduli space of stable rank 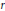 $r$ , degree
$r$ , degree 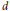 $d$ vector bundles on a smooth projective curve. We do not assume
$d$ vector bundles on a smooth projective curve. We do not assume 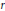 $r$ and
$r$ and 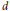 $d$ are coprime. In the process we equip the cohomology of an arbitrary algebraic stack with a functorial mixed Hodge structure. This Hodge structure is computed in the case of the moduli stack of rank
$d$ are coprime. In the process we equip the cohomology of an arbitrary algebraic stack with a functorial mixed Hodge structure. This Hodge structure is computed in the case of the moduli stack of rank 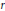 $r$ , degree
$r$ , degree 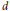 $d$ vector bundles on a curve. Our methods also yield a formula for the Poincaré polynomial of the moduli stack that is valid over any ground field. In the last section we use the previous sections to give a proof that the Tamagawa number of
$d$ vector bundles on a curve. Our methods also yield a formula for the Poincaré polynomial of the moduli stack that is valid over any ground field. In the last section we use the previous sections to give a proof that the Tamagawa number of 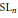 $\text{S}{{\text{L}}_{n}}$ is one.
$\text{S}{{\text{L}}_{n}}$ is one.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2006
References
- 8
- Cited by

