No CrossRef data available.
Article contents
On a Stein And Weiss Property of the Conjugate Function
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
(1.1) The conjugate function on locally compact abelian groups. Let G be a locally compact abelian group with character group Ĝ. Let μ denote a Haar measure on G such that μ(G) = 1 if G is compact. (Unless stated otherwise, all the measures referred to below are Haar measures on the underlying groups.) Suppose that Ĝ contains a measurable order P: P + P ⊆P; PU(-P)= Ĝ; and P⋂(—P) =﹛0﹜. For ƒ in ℒ2(G), the conjugate function of f (with respect to the order P) is the function 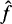 whose Fourier transform satisfies the identity
whose Fourier transform satisfies the identity 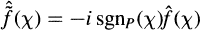 for almost all χ in Ĝ, where sgnP(χ)= 0, 1, or —1, according as χ =0, χ ∈ P\\﹛0﹜, or χ ∈ (—P)\﹛0﹜.
for almost all χ in Ĝ, where sgnP(χ)= 0, 1, or —1, according as χ =0, χ ∈ P\\﹛0﹜, or χ ∈ (—P)\﹛0﹜.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1990
References
1.
Asmar, N., Exponential estimates for the conjugate function on locally compact abelian groups, Can. Math. Bull., (to appear).Google Scholar
2.
Asmar, N., Earl Berkson, and Gillespie, T.A., Representation of groups with ordered duals and
generalized analyticity, J. of Funct. Anal, (to appear).Google Scholar
3.
Asmar, N. and Edwin Hewitt, Marcel Riesz's theorem on conjugate Fourier series and its descendants, Proceedings of the Analysis Conference (Singapore, 1986). North-Hoi land, Mathematics Series 150 (Elsevier Publishers, New York, 1988), 1–56.Google Scholar
4.
Berkson, E., and Gillespie, T.A., The generalized M. Riesz theorem and transference, Pacific J. Math.
120 (1985), 279–288.Google Scholar
6.
Calderón, A., Ergodic theory and translation-invariant operators, Proc. Nat. Acad. Sc, U.S.A.
59 (1968), 349–353.Google Scholar
7.
Coifman, R.R. and Weiss, G., Transference methods in analysis, Regional Conference Series in Math. 31 (Amer. Math. Soc, Providence, R.I., 1977).Google Scholar
8. Edwin Hewitt and Koshi, S., Orderings in locally compact abelian groups and the theorem of F. and M. Riesz, Mat. Proc. of Camb. Phil. Soc.
93 (1983), 441–457.Google Scholar
9.
Hewitt, Edwin and Ross, K.A., Abstract harmonic analysis, Vol. I, Grundlehren der mathematischen Wissenschaften 115, Second Edition (Springer-Verlag, 1970).Google Scholar
10.
Hewitt, Edwin and Ross, K.A., Abstract harmonic analysis, Vol. II, Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen 152 (Berlin, Heidelberg, New York, 1970).Google Scholar
11.
Hewitt, Edwin and Stromberg, K., Real and abstract analysis, Graduate Texts in Mathematics 25, (Berlin, Heidelberg, New York: Springer, 1969).Google Scholar
12.
Oberhettinger, F., Tabellen zur Fourier Transformation, Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen 90 (Berlin, Göttingen, Heidelberg, Springer-Verlag, 1957).Google Scholar
13.
Stein, E.M. and Weiss, G., An extension of a theorem of Marcinkiewicz and some applications,
Journal of Math, and Mechanics
8 (1959), 263–284.Google Scholar
14.
Stein, E.M. and Weiss, G., Introduction to Fourier analysis on Euclidean spaces, 2nd Printing (Princeton Mathematical Series, Princeton Univ. Press, Princeton, New Jersey, 1975).Google Scholar
15.
Zygmund, A., Trigonometric series, Vol. I and II (Cambridge University Press, Second Edition, 1959).Google Scholar

