Hostname: page-component-5b777bbd6c-6lqsf Total loading time: 0 Render date: 2025-06-18T23:28:24.691Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimum non-chromatic-choosable graphs with given chromatic number

Part of: Graph theory

Published online by Cambridge University Press:  27 December 2024

Jialu Zhu  and
Xuding Zhu
Jialu Zhu
Affiliation:
School of Mathematical Sciences, Zhejiang Normal University, Jinhua, China e-mail: jialuzhu@zjnu.edu.cn
Xuding Zhu*
Affiliation:
School of Mathematical Sciences, Zhejiang Normal University, Jinhua, China e-mail: jialuzhu@zjnu.edu.cn
*
e-mail: xdzhu@zjnu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

A graph G is called chromatic-choosable if 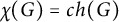$\chi (G)=ch(G)$. A natural problem is to determine the minimum number of vertices in a non-chromatic-choosable graph with given chromatic number. It was conjectured by Ohba, and proved by Noel, Reed, and Wu that k-chromatic graphs G with 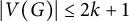$|V(G)| \le 2k+1$ are chromatic-choosable. This upper bound on 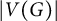$|V(G)|$ is tight. It is known that if k is even, then 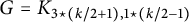$G=K_{3 \star (k/2+1), 1 \star (k/2-1)}$ and 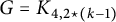$G=K_{4, 2 \star (k-1)}$ are non-chromatic-choosable k-chromatic graphs with 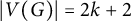$|V(G)| =2 k+2$. Some subgraphs of these two graphs are also non-chromatic-choosable. The main result of this paper is that all other k-chromatic graphs G with 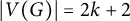$|V(G)| =2 k+2$ are chromatic-choosable. In particular, if 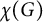$\chi (G)$ is odd and 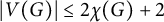$|V(G)| \le 2\chi (G)+2$, then G is chromatic-choosable, which was conjectured by Noel.

Keywords

Chromatic-choosable graphsOhba conjectureNoel conjecturenear acceptable L-coloringextremal graphs

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 32
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was supported by the NSFC (Grant Nos. 12371359 and U20A2068).

References

Bollobás, B. and Harris, A. J., List-colourings of graphs . Graphs Combin. 1(1985), no. 2, 115–127.Google Scholar
Chang, F., Chen, H., Guo, J., and Huang, Y., On-line choice number of complete multipartite graphs: An algorithmic approach . Electron. J. Combin. 22(2015), no. 1, p. 1.6, 16p.Google Scholar
Enomoto, H., Ohba, K., Ota, K., and Sakamoto, J., Choice number of some complete multi-partite graphs . Discrete Math. 244(2002), nos. 1–3, 55–66.Google Scholar
Erdős, P., Rubin, A. L., and Taylor, H., Choosability in graphs . In: Proceedings of the west coast conference on combinatorics, graph theory and computing, Humboldt State University, Arcata, California, Congress. Numer., XXVI, Utilitas Mathematica, Winnipeg, MB, 1980, pp. 125–157.Google Scholar
Galvin, F., The list chromatic index of a bipartite multigraph . J. Combin. Theory Ser. B 63(1995), no.1, 153–158.Google Scholar
Gravier, S. and Maffray, F., Graphs whose choice number is equal to their chromatic number . J. Graph Theory 27(1998), no.2, 87–97.Google Scholar
Häggkvist, R. and Chetwynd, A., Some upper bounds on the total and list chromatic numbers of multigraphs . J. Graph Theory 16(1992), no.5, 503–516.Google Scholar
Huang, P., Wong, T., and Zhu, X., Application of polynomial method to on-line list colouring of graphs . Eur. J. Combin. 33(2012), no. (5), 872–883.Google Scholar
He, W., Zhang, L., Cranston, D. W., Shen, Y., and Zheng, G., Choice number of complete multipartite graphs ${K}_{3\star 3,2\star \left(k-5\right),1\star 2}$ . Discrete Math. 308(2008), no. 23, 5871–5877.Google Scholar
Jensen, T. R. and Toft, B., Graph coloring problems, Wiley-Interscience Series in Discrete Mathematics and Optimization, John Wiley & Sons Inc., New York, 1995.Google Scholar
Kierstead, H. A., On the choosability of complete multipartite graphs with part size three . Discrete Math. 211(2000), nos. 1–3, 255–259.Google Scholar
Kim, S., Kwon, Y., Liu, D., and Zhu, X., On-line list colouring of complete multipartite graphs . Electron. J. Combin. 19(2012), no. 1, p. 41, 13.Google Scholar
Kostochka, A. V., Stiebitz, M., and Woodall, D. R., Ohba’s conjecture for graphs with independence number five . Discrete Math. 311(2011), no. 12, 996–1005.Google Scholar
Kozik, J., Micek, P., and Zhu, X., Towards an on-line version of Ohba’s conjecture . European J. Combin. 36(2014), 110–121.Google Scholar
Noel, J. A., Choosability of graphs with bounded order: Ohba’s conjecture and beyond. Master’s thesis, McGill University, Montréal, QC, 2013.Google Scholar
Noel, J. A., West, D. B., Wu, H., and Zhu, X., Beyond Ohba’s conjecture: A bound on the choice number of $k$ -chromatic graphs with $n$ vertices . Eur. J. Combin. 43(2015), 295–305.Google Scholar
Noel, J. A., Reed, B. A., and Wu, H., A proof of a conjecture of Ohba . J. Graph Theory 79(2015), no.2, 86–102.Google Scholar
Ohba, K., On chromatic-choosable graphs . J. Graph Theory 40(2002), no. 2, 130–135.Google Scholar
Ohba, K., Choice number of complete multipartite graphs with part size at most three . Ars Combin. 72(2004), 133–139.Google Scholar
Reed, B. and Sudakov, B., List colouring of graphs with at most $\left(2-o(1)\right)\chi$ vertices. In. Proceedings of the international congress of mathematicians, Vol. III (Beijing, 2002), Higher Education Press, Beijing, 2002, pp. 587–603.Google Scholar
Reed, B. and Sudakov, B., List colouring when the chromatic number is close to the order of the graph . Combinatorica 25(2005), no. 1, 117–123.Google Scholar
Shen, Y., He, W., Zheng, G., and Li, Y., Ohba’s conjecture is true for graphs with independence number at most three . Appl. Math. Lett. 22(2009), no.6, 938–942.Google Scholar
Shen, Y., He, W., Zheng, G., Wang, Y., and Zhang, L., On choosability of some complete multipartite graphs and Ohba’s conjecture . Discrete Math. 308(2008), no.1, 136–143.Google Scholar
Vizing, V. G., Coloring the vertices of a graph in prescribed colors . Diskret. Analiz 101(1976), no. 29, 3–10. Metody Diskret. Anal. v Teorii Kodov i Shem.Google Scholar
Zeilberger, D., The method of undetermined generalization and specialization illustrated with Fred Galvin’s amazing proof of the Dinitz conjecture . Amer. Math. Mon. 103(1996), no. 3, 233–239.Google Scholar