Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Goldstern, Martin
Schmeling, Jörg
and
Winkler, Reinhard
2000.
Metric, Fractal Dimensional and Baire Results on the Distribution of Subsequences.
Mathematische Nachrichten,
Vol. 219,
Issue. 1,
p.
97.

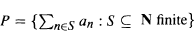 for a certain sequence
for a certain sequence 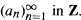 The main questions studied here are : (1) Under what conditions on (
The main questions studied here are : (1) Under what conditions on (