Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Smith, Tara L.
1994.
Extra-Special Groups of Order 32 as Galois Groups.
Canadian Journal of Mathematics,
Vol. 46,
Issue. 4,
p.
886.
Ledet, Arne
1995.
On 2-Groups as Galois Groups.
Canadian Journal of Mathematics,
Vol. 47,
Issue. 6,
p.
1253.
Dentzer, Ralf
1995.
On geometric embedding problems and semiabelian groups.
Manuscripta Mathematica,
Vol. 86,
Issue. 1,
p.
199.
Drees, Christof
Epkenhans, Martin
and
Krüskemper, Martin
1997.
On the Computation of the Trace Form of Some Galois Extensions.
Journal of Algebra,
Vol. 192,
Issue. 1,
p.
209.
Lemmermeyer, Franz
1997.
Unramified quaternion extensions of quadratic number fields.
Journal de théorie des nombres de Bordeaux,
Vol. 9,
Issue. 1,
p.
51.
Ledet, Arne
1998.
Embedding problems with cyclic kernel of order 4.
Israel Journal of Mathematics,
Vol. 106,
Issue. 1,
p.
109.
Black, Elena
1999.
Deformations of dihedral 2-group extensions of fields.
Transactions of the American Mathematical Society,
Vol. 351,
Issue. 8,
p.
3229.
Ledet, Arne
1999.
Generic polynomials for quasi-dihedral, dihedral and modular extensions of order 16.
Proceedings of the American Mathematical Society,
Vol. 128,
Issue. 8,
p.
2213.
Ledet, Arne
2000.
Generic and Explicit Realization of Smallp-groups.
Journal of Symbolic Computation,
Vol. 30,
Issue. 6,
p.
859.
Michailov, Ivo M.
and
Ziapkov, Nikola P.
2000.
Embedding Obstructions for the Generalized Quaternion Group.
Journal of Algebra,
Vol. 226,
Issue. 1,
p.
375.
Ledet, Arne
2000.
Generic Extensions and Generic Polynomials.
Journal of Symbolic Computation,
Vol. 30,
Issue. 6,
p.
867.
Michailov, Ivo M
2001.
Embedding Obstructions for the Dihedral, Semidihedral, and Quaternion 2-Groups.
Journal of Algebra,
Vol. 245,
Issue. 1,
p.
355.
Swallow, John R.
2001.
QUADRATIC DESCENT FOR QUATERNION ALGEBRAS.
Communications in Algebra,
Vol. 29,
Issue. 10,
p.
4523.
Hwang, Y.-S.
Leep, David B.
and
Wadsworth, Adrian R.
2003.
Galois groups of order 2n that contain a cyclic subgroup of order n.
Pacific Journal of Mathematics,
Vol. 212,
Issue. 2,
p.
297.
Grundman, Helen G.
and
Stewart, Grisha L.
2004.
Galois realizability of non-split group extensions of C2 by (C2)r×(C4)s×(D4)t.
Journal of Algebra,
Vol. 272,
Issue. 2,
p.
425.
Michailov, Ivo M.
2007.
Four non-abelian groups of order p4 as Galois groups.
Journal of Algebra,
Vol. 307,
Issue. 1,
p.
287.
Geyer, Wulf-Dieter
and
Jensen, Christian U
2007.
Embeddability of quadratic extensions in cyclic extensions.
Forum Mathematicum,
Vol. 19,
Issue. 4,
Michailov, Ivo M.
2011.
On Galois cohomology and realizability of 2-groups as Galois groups.
Central European Journal of Mathematics,
Vol. 9,
Issue. 2,
p.
403.
Hoshi, Akinari
Kang, Ming-chang
and
Kitayama, Hidetaka
2014.
Quasi-monomial actions and some 4-dimensional rationality problems.
Journal of Algebra,
Vol. 403,
Issue. ,
p.
363.
SHANKAR, ARUL
SÖDERGREN, ANDERS
and
TEMPLIER, NICOLAS
2019.
SATO–TATE EQUIDISTRIBUTION OF CERTAIN FAMILIES OF ARTIN -FUNCTIONS.
Forum of Mathematics, Sigma,
Vol. 7,
Issue. ,

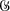 be a finite group. Let
be a finite group. Let 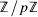 , where
, where 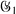 the Galois group of
the Galois group of