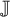1 Introduction
Affine Deligne–Lusztig varieties were introduced by Rapoport [Reference Rapoport34], which play an important role in understanding geometric and arithmetic properties of Shimura varieties. The uniformization theorem by Rapoport and Zink [Reference Rapoport and Zink33] allows us to describe the Newton strata of Shimura varieties in terms of Rapoport–Zink spaces, whose underlying spaces are special cases of affine Deligne–Lusztig varieties.
Let F be a non-Archimedean local field with finite residue field
![]() $\mathbb {F}_q$
of prime characteristic p, and let L be the completion of the maximal unramified extension of F. Let
$\mathbb {F}_q$
of prime characteristic p, and let L be the completion of the maximal unramified extension of F. Let
![]() $\sigma $
denote the Frobenius automorphism of
$\sigma $
denote the Frobenius automorphism of
![]() $L/F$
. Further, we write
$L/F$
. Further, we write
![]() $\mathcal O$
(resp.
$\mathcal O$
(resp.
![]() $\mathcal O_F$
) for the valuation ring of L (resp. F). Finally, we denote by
$\mathcal O_F$
) for the valuation ring of L (resp. F). Finally, we denote by
![]() $\varpi $
a uniformizer of F (and L) and by
$\varpi $
a uniformizer of F (and L) and by
![]() $v_L$
the valuation of L such that
$v_L$
the valuation of L such that
![]() $v_L(\varpi )=1$
.
$v_L(\varpi )=1$
.
Let G be an unramified connected reductive group over
![]() $\mathcal O_F$
. Let
$\mathcal O_F$
. Let
![]() $B\subset G$
be a Borel subgroup and
$B\subset G$
be a Borel subgroup and
![]() $T\subset B$
a maximal torus in B, both defined over
$T\subset B$
a maximal torus in B, both defined over
![]() $\mathcal O_F$
. For
$\mathcal O_F$
. For
![]() $\mu ,\mu '\in X_*(T)$
(resp.
$\mu ,\mu '\in X_*(T)$
(resp.
![]() $X_*(T)_{\mathbb Q}$
), we write
$X_*(T)_{\mathbb Q}$
), we write
![]() $\mu '\preceq \mu $
if
$\mu '\preceq \mu $
if
![]() $\mu -\mu '$
is a nonnegative integral (resp. rational) linear combination of positive coroots. For a cocharacter
$\mu -\mu '$
is a nonnegative integral (resp. rational) linear combination of positive coroots. For a cocharacter
![]() $\mu \in X_*(T)$
, let
$\mu \in X_*(T)$
, let
![]() $\varpi ^{\mu }$
be the image of
$\varpi ^{\mu }$
be the image of
![]() $\varpi \in \mathbb G_m(F)$
under the homomorphism
$\varpi \in \mathbb G_m(F)$
under the homomorphism
![]() $\mu \colon \mathbb G_m\rightarrow T$
.
$\mu \colon \mathbb G_m\rightarrow T$
.
Set
![]() $K=G(\mathcal O)$
. We fix a dominant cocharacter
$K=G(\mathcal O)$
. We fix a dominant cocharacter
![]() $\mu \in X_*(T)_+$
and
$\mu \in X_*(T)_+$
and
![]() $b\in G(L)$
. Then the affine Deligne–Lusztig variety
$b\in G(L)$
. Then the affine Deligne–Lusztig variety
![]() $X_{\mu }(b)$
is the locally closed reduced
$X_{\mu }(b)$
is the locally closed reduced
![]() $\overline {\mathbb F}_q$
-subscheme of the affine Grassmannian
$\overline {\mathbb F}_q$
-subscheme of the affine Grassmannian
![]() ${\mathcal {G}} r=G(L)/K$
defined as
${\mathcal {G}} r=G(L)/K$
defined as
The closed affine Deligne–Lusztig variety is the closed reduced
![]() $\overline {\mathbb F}_q$
-subscheme of
$\overline {\mathbb F}_q$
-subscheme of
![]() ${\mathcal {G}} r$
defined as
${\mathcal {G}} r$
defined as
Both
![]() $X_{\mu }(b)$
and
$X_{\mu }(b)$
and
![]() $X_{\preceq \mu }(b)$
are locally of finite type in the equal characteristic case and locally perfectly of finite type in the mixed characteristic case (cf. [Reference Hartl and Viehmann19, Corollary 6.5], [Reference Hamacher and Viehmann18, Lemma 1.1]). Finally, the affine Deligne–Lusztig varieties
$X_{\preceq \mu }(b)$
are locally of finite type in the equal characteristic case and locally perfectly of finite type in the mixed characteristic case (cf. [Reference Hartl and Viehmann19, Corollary 6.5], [Reference Hamacher and Viehmann18, Lemma 1.1]). Finally, the affine Deligne–Lusztig varieties
![]() $X_{\mu }(b)$
and
$X_{\mu }(b)$
and
![]() $X_{\preceq \mu }(b)$
carry a natural action (by left multiplication) by the
$X_{\preceq \mu }(b)$
carry a natural action (by left multiplication) by the
![]() $\sigma $
-centralizer of b
$\sigma $
-centralizer of b
The geometric properties of affine Deligne–Lusztig varieties have been studied by many people. For example, the non-emptiness criterion and the dimension formula are already known for the affine Deligne–Lusztig varieties in the affine Grassmannian (see [Reference Gashi8], [Reference Viehmann42] and [Reference Hamacher17]). Let
![]() $B(G)$
denote the set of
$B(G)$
denote the set of
![]() $\sigma $
-conjugacy classes of
$\sigma $
-conjugacy classes of
![]() $G(L)$
. Thanks to Kottwitz [Reference Kottwitz28], a
$G(L)$
. Thanks to Kottwitz [Reference Kottwitz28], a
![]() $\sigma $
-conjugacy class
$\sigma $
-conjugacy class
![]() $[b]\in B(G)$
is uniquely determined by two invariants: the Kottwitz point
$[b]\in B(G)$
is uniquely determined by two invariants: the Kottwitz point
![]() $\kappa (b)\in \pi _1(G)/((1-\sigma )\pi _1(G))$
and the Newton point
$\kappa (b)\in \pi _1(G)/((1-\sigma )\pi _1(G))$
and the Newton point
![]() $\nu _b\in X_*(T)_{\mathbb Q,+}$
. Set
$\nu _b\in X_*(T)_{\mathbb Q,+}$
. Set
![]() $B(G,\mu )=\{[b]\in B(G)\mid \kappa (b)=\kappa (\varpi ^\mu ), \nu _b\preceq \mu ^{\diamond }\}$
, where
$B(G,\mu )=\{[b]\in B(G)\mid \kappa (b)=\kappa (\varpi ^\mu ), \nu _b\preceq \mu ^{\diamond }\}$
, where
![]() $\mu ^{\diamond }\in X_*(T)_{\mathbb Q,+}$
denotes the
$\mu ^{\diamond }\in X_*(T)_{\mathbb Q,+}$
denotes the
![]() $\sigma $
-average of
$\sigma $
-average of
![]() $\mu $
. Then
$\mu $
. Then
![]() $X_\mu (b)\neq \emptyset $
if and only if
$X_\mu (b)\neq \emptyset $
if and only if
![]() $[b]\in B(G,\mu )$
. If this is the case, then we have
$[b]\in B(G,\mu )$
. If this is the case, then we have
where
![]() $\rho $
is the half sum of positive roots and
$\rho $
is the half sum of positive roots and
![]() $\operatorname {\mathrm {def}}(b)$
is the defect of b. Moreover, the parametrization problem of the set of irreducible components
$\operatorname {\mathrm {def}}(b)$
is the defect of b. Moreover, the parametrization problem of the set of irreducible components
![]() $\operatorname {\mathrm {Irr}} X_\mu (b)$
is also known. Let
$\operatorname {\mathrm {Irr}} X_\mu (b)$
is also known. Let
![]() $\widehat G$
be the Langlands dual of G defined over
$\widehat G$
be the Langlands dual of G defined over
![]() $\overline {\mathbb Q}_l$
with
$\overline {\mathbb Q}_l$
with
![]() $l\neq p$
. Surprisingly, there exists a natural bijection between
$l\neq p$
. Surprisingly, there exists a natural bijection between
![]() $J_b(F)\backslash \operatorname {\mathrm {Irr}} X_\mu (b)$
and a certain weight space of the crystal basis
$J_b(F)\backslash \operatorname {\mathrm {Irr}} X_\mu (b)$
and a certain weight space of the crystal basis
![]() $\mathbb B_\mu $
of the irreducible
$\mathbb B_\mu $
of the irreducible
![]() $\widehat G$
-module
$\widehat G$
-module
![]() $V_\mu $
of highest weight
$V_\mu $
of highest weight
![]() $\mu $
. This is conjectured by Chen and Zhu, and proved in general by Nie [Reference Nie32] and Zhou-Zhu [Reference Zhou and Zhu47].
$\mu $
. This is conjectured by Chen and Zhu, and proved in general by Nie [Reference Nie32] and Zhou-Zhu [Reference Zhou and Zhu47].
Via the relationship to Shimura varieties, or more directly to Rapoport–Zink spaces, the results on the geometry of affine Deligne–Lusztig varieties have numerous applications to number theory (e.g., the Kudla-Rapoport program [Reference Kudla and Rapoport29], Zhang’s Arithmetic Fundamental Lemma [Reference Zhang46],
![]() $\ldots $
). Many of these applications make use of the special cases where
$\ldots $
). Many of these applications make use of the special cases where
![]() $X_{\preceq \mu }(b)$
admits a simple description. The fully Hodge–Newton decomposable case, introduced by Görtz, He and Nie [Reference Görtz, He and Nie13], is one of such cases. They proved that
$X_{\preceq \mu }(b)$
admits a simple description. The fully Hodge–Newton decomposable case, introduced by Görtz, He and Nie [Reference Görtz, He and Nie13], is one of such cases. They proved that
![]() $(G, \mu )$
is fully Hodge–Newton decomposable if and only if
$(G, \mu )$
is fully Hodge–Newton decomposable if and only if
![]() $X_{\preceq \mu }(\tau _\mu )$
is naturally a union of (classical) Deligne–Lusztig varieties (in fact, they studied the cases with arbitrary parahoric level). This stratification is the so-called weak Bruhat-Tits stratification, a stratification indexed in terms of the Bruhat-Tits building of
$X_{\preceq \mu }(\tau _\mu )$
is naturally a union of (classical) Deligne–Lusztig varieties (in fact, they studied the cases with arbitrary parahoric level). This stratification is the so-called weak Bruhat-Tits stratification, a stratification indexed in terms of the Bruhat-Tits building of
![]() $J_b(F)$
(which exists only in the fully Hodge–Newton decomposable case). The case of Coxeter type is a special case of this case such that each Deligne-Lusztig variety appearing in this stratification is of Coxeter type (cf. [Reference Görtz, He and Nie14, Section 2.3]). In this case, we drop the “weak” above. For example, the cases of Coxeter type include the case for certain unitary groups of signature
$J_b(F)$
(which exists only in the fully Hodge–Newton decomposable case). The case of Coxeter type is a special case of this case such that each Deligne-Lusztig variety appearing in this stratification is of Coxeter type (cf. [Reference Görtz, He and Nie14, Section 2.3]). In this case, we drop the “weak” above. For example, the cases of Coxeter type include the case for certain unitary groups of signature
![]() $(1, n-1)$
studied in [Reference Vollaard and Wedhorn44] by Vollaard and Wedhorn, which has been used in [Reference Kudla and Rapoport29] and [Reference Zhang46].
$(1, n-1)$
studied in [Reference Vollaard and Wedhorn44] by Vollaard and Wedhorn, which has been used in [Reference Kudla and Rapoport29] and [Reference Zhang46].
To give a conceptual way to explain the relationship between the geometry of affine Deligne–Lusztig varieties and the Bruhat-Tits building of
![]() $J_b(F)$
indicated by above examples, Chen and Viehmann [Reference Chen and Viehmann2] introduced the
$J_b(F)$
indicated by above examples, Chen and Viehmann [Reference Chen and Viehmann2] introduced the
![]() $\mathbb J$
-stratification, where
$\mathbb J$
-stratification, where
![]() $\mathbb J$
stands for
$\mathbb J$
stands for
![]() $J_b(F)$
. The
$J_b(F)$
. The
![]() $\mathbb J$
-strata are locally closed subsets of
$\mathbb J$
-strata are locally closed subsets of
![]() ${\mathcal {G}} r$
. By intersecting each
${\mathcal {G}} r$
. By intersecting each
![]() $\mathbb J$
-stratum with
$\mathbb J$
-stratum with
![]() $X_{\preceq \mu }(b)$
, we obtain the
$X_{\preceq \mu }(b)$
, we obtain the
![]() $\mathbb J$
-stratification of
$\mathbb J$
-stratification of
![]() $X_{\preceq \mu }(b)$
(see Section 2.4 for details). In [Reference Görtz9], Görtz showed that the Bruhat-Tits stratification coincides with the
$X_{\preceq \mu }(b)$
(see Section 2.4 for details). In [Reference Görtz9], Görtz showed that the Bruhat-Tits stratification coincides with the
![]() $\mathbb J$
-stratification. In fact the Bruhat-Tits stratification is a refinement of the Ekedahl–Oort stratification (see Section 2.2 for the latter). So the
$\mathbb J$
-stratification. In fact the Bruhat-Tits stratification is a refinement of the Ekedahl–Oort stratification (see Section 2.2 for the latter). So the
![]() $\mathbb J$
-stratification is also a refinement of the Ekedahl–Oort stratification when
$\mathbb J$
-stratification is also a refinement of the Ekedahl–Oort stratification when
![]() $(G,\mu )$
is of Coxeter type. This does not hold in general even if
$(G,\mu )$
is of Coxeter type. This does not hold in general even if
![]() $\mu $
is minuscule. See [Reference Chen and Viehmann2, Example 4.1] for a counterexample in the case
$\mu $
is minuscule. See [Reference Chen and Viehmann2, Example 4.1] for a counterexample in the case
![]() $G=\operatorname {\mathrm {GL}}_9$
. Therefore, the cases when the
$G=\operatorname {\mathrm {GL}}_9$
. Therefore, the cases when the
![]() $\mathbb J$
-stratification is a refinement of the Ekedahl–Oort stratification should be special cases, which are of particular interest.
$\mathbb J$
-stratification is a refinement of the Ekedahl–Oort stratification should be special cases, which are of particular interest.
Usually it seems very difficult to study the
![]() $\mathbb J$
-stratification. However, in the case that
$\mathbb J$
-stratification. However, in the case that
![]() $G=\operatorname {\mathrm {GL}}_n$
and b is superbasic (i.e.,
$G=\operatorname {\mathrm {GL}}_n$
and b is superbasic (i.e.,
![]() $\kappa (b)\in \mathbb Z$
is coprime to n), the
$\kappa (b)\in \mathbb Z$
is coprime to n), the
![]() $\mathbb J$
-stratification coincides with a stratification by semi-modules [Reference Chen and Viehmann2, Proposition 3.4]. The notion of semi-modules was first considered by de Jong and Oort [Reference de Jong and Oort3] (see Section 3.1) for minuscule cocharacters. Later Viehmann [Reference Viehmann42] introduced a notion of extended semi-modules for arbitrary cocharacters, which generalizes the notion of semi-modules. It played a crucial role to prove the dimension formula (for split groups) and the Chen-Zhu conjecture mentioned above. This is because for these problems, we can reduce the general case to the case that
$\mathbb J$
-stratification coincides with a stratification by semi-modules [Reference Chen and Viehmann2, Proposition 3.4]. The notion of semi-modules was first considered by de Jong and Oort [Reference de Jong and Oort3] (see Section 3.1) for minuscule cocharacters. Later Viehmann [Reference Viehmann42] introduced a notion of extended semi-modules for arbitrary cocharacters, which generalizes the notion of semi-modules. It played a crucial role to prove the dimension formula (for split groups) and the Chen-Zhu conjecture mentioned above. This is because for these problems, we can reduce the general case to the case that
![]() $G=\operatorname {\mathrm {GL}}_n$
and b is superbasic.
$G=\operatorname {\mathrm {GL}}_n$
and b is superbasic.
The aim of this paper is to compare the Ekedahl–Oort stratification and the semi-module stratification (for
![]() $G=\operatorname {\mathrm {GL}}_n$
). To state the main results, we need some notation. Let
$G=\operatorname {\mathrm {GL}}_n$
). To state the main results, we need some notation. Let
![]() $W_0$
be the (finite) Weyl group of T in G and let
$W_0$
be the (finite) Weyl group of T in G and let
![]() $\tilde W$
be the Iwahori-Weyl group of T in G. Then
$\tilde W$
be the Iwahori-Weyl group of T in G. Then
![]() $\tilde W=X_*(T)\rtimes W_0$
. We denote the projection
$\tilde W=X_*(T)\rtimes W_0$
. We denote the projection
![]() $\tilde W\rightarrow W_0$
by p. For
$\tilde W\rightarrow W_0$
by p. For
![]() $\mu \in X_*(T)_+$
, we denote by
$\mu \in X_*(T)_+$
, we denote by
![]() $\operatorname {\mathrm {Adm}}(\mu )$
the admissible subset of
$\operatorname {\mathrm {Adm}}(\mu )$
the admissible subset of
![]() $\tilde W$
. Let
$\tilde W$
. Let
![]() ${^S\mathrm {Adm}}(\mu )$
be a certain subset of
${^S\mathrm {Adm}}(\mu )$
be a certain subset of
![]() $\operatorname {\mathrm {Adm}}(\mu )$
, which is the index set of the Ekedahl–Oort stratification of
$\operatorname {\mathrm {Adm}}(\mu )$
, which is the index set of the Ekedahl–Oort stratification of
![]() $X_{\preceq \mu }(\tau _\mu )$
(see Section 2.2). We fix (a representative in
$X_{\preceq \mu }(\tau _\mu )$
(see Section 2.2). We fix (a representative in
![]() $G(L)$
of a) length
$G(L)$
of a) length
![]() $0$
element
$0$
element
![]() $\tau _\mu \in \tilde W$
whose
$\tau _\mu \in \tilde W$
whose
![]() $\sigma $
-conjugacy class in
$\sigma $
-conjugacy class in
![]() $G(L)$
is the unique basic element in
$G(L)$
is the unique basic element in
![]() $B(G,\mu )$
. Finally, let
$B(G,\mu )$
. Finally, let
![]() $\operatorname {\mathrm {LP}}(w)\subseteq W_0$
be the length positive elements for w (see Section 2.5).
$\operatorname {\mathrm {LP}}(w)\subseteq W_0$
be the length positive elements for w (see Section 2.5).
Theorem A (See Theorem 7.2)
Let
![]() $G=\operatorname {\mathrm {GL}}_n$
and let
$G=\operatorname {\mathrm {GL}}_n$
and let
![]() $\mu \in X_*(T)_+$
. Assume that
$\mu \in X_*(T)_+$
. Assume that
![]() $\tau _\mu $
is superbasic. Then the following assertions are equivalent.
$\tau _\mu $
is superbasic. Then the following assertions are equivalent.
-
(i) The
 $\mathbb J$
-stratification (or the semi-module stratification) of
$\mathbb J$
-stratification (or the semi-module stratification) of
 $X_{\preceq \mu }(\tau _\mu )(\neq \emptyset )$
gives a refinement of the Ekedahl–Oort stratification.
$X_{\preceq \mu }(\tau _\mu )(\neq \emptyset )$
gives a refinement of the Ekedahl–Oort stratification. -
(ii) For any
 $w\in {^S{\operatorname {\mathrm {Adm}}}}(\mu )$
whose corresponding Ekedahl–Oort stratum is nonempty, there exists
$w\in {^S{\operatorname {\mathrm {Adm}}}}(\mu )$
whose corresponding Ekedahl–Oort stratum is nonempty, there exists
 $v\in \operatorname {\mathrm {LP}}(w)$
such that
$v\in \operatorname {\mathrm {LP}}(w)$
such that
 $v^{-1}p(w)v$
is a Coxeter element.
$v^{-1}p(w)v$
is a Coxeter element. -
(iii) The cocharacter
 $\mu $
has one of the following forms modulo
$\mu $
has one of the following forms modulo
 $\mathbb Z\omega _n$
:
$\mathbb Z\omega _n$
:  $$ \begin{align*} &\omega_1,\quad \omega_{n-1},\ &(n\geq 1),\\ &\omega_2,\quad 2\omega_1,\quad \omega_{n-2},\quad 2\omega_{n-1},\ &(\mathit{odd}\ n\geq 3),\\ &\omega_2+\omega_{n-1},\quad 2\omega_1+\omega_{n-1}\quad \omega_1+\omega_{n-2},\quad\omega_1+2\omega_{n-1},\ &(n\geq 3),\\ &\omega_3,\quad\omega_{n-3},\ &(n=7,8),\\ &3\omega_1,\quad 3\omega_{n-1},\ &(n=4,5),\\ &\omega_1+\omega_2,\quad\omega_3+\omega_4,\ &(n=5),\\ &4\omega_1,\quad \omega_1+3\omega_2,\quad 4\omega_2,\quad 3\omega_1+\omega_2, &(n=3),\\ &m\omega_1\ \mathit{with}\ m\ \mathit{odd,} &(n=2). \end{align*} $$
$$ \begin{align*} &\omega_1,\quad \omega_{n-1},\ &(n\geq 1),\\ &\omega_2,\quad 2\omega_1,\quad \omega_{n-2},\quad 2\omega_{n-1},\ &(\mathit{odd}\ n\geq 3),\\ &\omega_2+\omega_{n-1},\quad 2\omega_1+\omega_{n-1}\quad \omega_1+\omega_{n-2},\quad\omega_1+2\omega_{n-1},\ &(n\geq 3),\\ &\omega_3,\quad\omega_{n-3},\ &(n=7,8),\\ &3\omega_1,\quad 3\omega_{n-1},\ &(n=4,5),\\ &\omega_1+\omega_2,\quad\omega_3+\omega_4,\ &(n=5),\\ &4\omega_1,\quad \omega_1+3\omega_2,\quad 4\omega_2,\quad 3\omega_1+\omega_2, &(n=3),\\ &m\omega_1\ \mathit{with}\ m\ \mathit{odd,} &(n=2). \end{align*} $$
Here,
![]() $\omega _k$
denotes the cocharacter of the form
$\omega _k$
denotes the cocharacter of the form
![]() $(1,\ldots ,1,0,\ldots ,0)$
in which
$(1,\ldots ,1,0,\ldots ,0)$
in which
![]() $1$
is repeated k times. Moreover, if one of the above conditions holds, then each
$1$
is repeated k times. Moreover, if one of the above conditions holds, then each
![]() $\mathbb J$
-stratum is universally homeomorphic to an affine space.
$\mathbb J$
-stratum is universally homeomorphic to an affine space.
See Section 2.4 for the reason why we choose
![]() $\tau _\mu $
. In fact, this choice is the reasonable one suggested in [Reference Chen and Viehmann2, Remark 2.1], which is unique in this case.
$\tau _\mu $
. In fact, this choice is the reasonable one suggested in [Reference Chen and Viehmann2, Remark 2.1], which is unique in this case.
Although the cocharacters
![]() $\omega _1$
and
$\omega _1$
and
![]() $\omega _{n-1}$
are of Coxeter type for any n, the cocharacters
$\omega _{n-1}$
are of Coxeter type for any n, the cocharacters
![]() $2\omega _1$
and
$2\omega _1$
and
![]() $\omega _2$
are of Coxeter type only when
$\omega _2$
are of Coxeter type only when
![]() $n=2$
and
$n=2$
and
![]() $n=4$
respectively (cf. [Reference Görtz, He and Nie14, Theorem 1.4]). In Theorem A, these two cocharacters are no longer exceptional cases. Note also that the condition (ii) works in more general setting. In [Reference Shimada38], we study this condition for
$n=4$
respectively (cf. [Reference Görtz, He and Nie14, Theorem 1.4]). In Theorem A, these two cocharacters are no longer exceptional cases. Note also that the condition (ii) works in more general setting. In [Reference Shimada38], we study this condition for
![]() $\operatorname {\mathrm {GL}}_n$
without the superbasic assumption. It turns out that if
$\operatorname {\mathrm {GL}}_n$
without the superbasic assumption. It turns out that if
![]() $\mu $
satisfies (ii), then the
$\mu $
satisfies (ii), then the
![]() $\mathbb J$
-stratification of
$\mathbb J$
-stratification of
![]() $X_{\preceq \mu }(\tau _\mu )$
gives a refinement of the Ekedahl–Oort stratification, and each
$X_{\preceq \mu }(\tau _\mu )$
gives a refinement of the Ekedahl–Oort stratification, and each
![]() $\mathbb J$
-stratum is universally homeomorphic to the product of a classical Deligne–Lusztig variety and an affine space. This simple description can be considered as a natural generalization of the Bruhat-Tits stratification. Moreover, in a joint work [Reference Schremmer, Shimada and Yu37] with Schremmer and Yu, we proved that (ii) implies a simple geometric structure on each Ekedahl–Oort stratum of
$\mathbb J$
-stratum is universally homeomorphic to the product of a classical Deligne–Lusztig variety and an affine space. This simple description can be considered as a natural generalization of the Bruhat-Tits stratification. Moreover, in a joint work [Reference Schremmer, Shimada and Yu37] with Schremmer and Yu, we proved that (ii) implies a simple geometric structure on each Ekedahl–Oort stratum of
![]() $X_{\preceq \mu }(\tau _\mu )$
for general G. In fact, the condition (ii) for
$X_{\preceq \mu }(\tau _\mu )$
for general G. In fact, the condition (ii) for
![]() $\operatorname {\mathrm {GL}}_n$
is also a generalization of Coxeter type [Reference Schremmer, Shimada and Yu37, Theorem 4.12]. So Theorem A tells us that the two conditions which contain the cases of Coxeter type are actually equivalent at least in the superbasic case.
$\operatorname {\mathrm {GL}}_n$
is also a generalization of Coxeter type [Reference Schremmer, Shimada and Yu37, Theorem 4.12]. So Theorem A tells us that the two conditions which contain the cases of Coxeter type are actually equivalent at least in the superbasic case.
If
![]() $\mu $
is minuscule and
$\mu $
is minuscule and
![]() $\operatorname {\mathrm {ch}} F=0$
, then
$\operatorname {\mathrm {ch}} F=0$
, then
![]() $X_{\mu }(\tau _\mu )(=X_{\preceq \mu }(\tau _\mu ))$
for
$X_{\mu }(\tau _\mu )(=X_{\preceq \mu }(\tau _\mu ))$
for
![]() $\operatorname {\mathrm {GL}}_n$
is the perfection of the special fiber of the Rapoport–Zink space attached to
$\operatorname {\mathrm {GL}}_n$
is the perfection of the special fiber of the Rapoport–Zink space attached to
![]() $(\operatorname {\mathrm {GL}}_n,\mu ,\tau _\mu )$
(cf. [Reference Görtz, He and Nie14, Section 5]). These Rapoport–Zink spaces are moduli spaces of p-divisible groups, which have been studied in [Reference Viehmann43]. Especially in the superbasic case, each
$(\operatorname {\mathrm {GL}}_n,\mu ,\tau _\mu )$
(cf. [Reference Görtz, He and Nie14, Section 5]). These Rapoport–Zink spaces are moduli spaces of p-divisible groups, which have been studied in [Reference Viehmann43]. Especially in the superbasic case, each
![]() $\mathbb J$
-stratum of
$\mathbb J$
-stratum of
![]() $X_{\mu }(\tau _\mu )$
is known to be isomorphic to an affine space (before perfection). However, even in this case, there is no good description of the closure of each
$X_{\mu }(\tau _\mu )$
is known to be isomorphic to an affine space (before perfection). However, even in this case, there is no good description of the closure of each
![]() $\mathbb J$
-stratum in general. On the other hand, it turned out in [Reference Shimada38] that if
$\mathbb J$
-stratum in general. On the other hand, it turned out in [Reference Shimada38] that if
![]() $\mu $
is a minuscule cocharacter appearing in the list (iii) above, then each
$\mu $
is a minuscule cocharacter appearing in the list (iii) above, then each
![]() $\mathbb J$
-stratum of
$\mathbb J$
-stratum of
![]() $X_{\mu }(\tau _\mu )$
can be written as a certain union of
$X_{\mu }(\tau _\mu )$
can be written as a certain union of
![]() $\mathbb J$
-strata. It is also worth mentioning that the condition (i) in Theorem A is essential to describe this union explicitly because we need to attach
$\mathbb J$
-strata. It is also worth mentioning that the condition (i) in Theorem A is essential to describe this union explicitly because we need to attach
![]() $w\in {^S\mathrm {Adm}}(\mu )$
to each
$w\in {^S\mathrm {Adm}}(\mu )$
to each
![]() $\mathbb J$
-stratum in a natural way (cf. [Reference Shimada38, Section 2.3]).
$\mathbb J$
-stratum in a natural way (cf. [Reference Shimada38, Section 2.3]).
In [Reference Chen and Tong1], Chen-Tong compared the Newton stratification and the Harder–Narashimhan stratification of the flag variety attached to
![]() $(G,\mu )$
under the assumption that
$(G,\mu )$
under the assumption that
![]() $\mu $
is minuscule. As a result, they showed that the former gives a refinement of the latter if and only if
$\mu $
is minuscule. As a result, they showed that the former gives a refinement of the latter if and only if
![]() $(G,\mu )$
is weakly fully Hodge–Newton decomposable [Reference Chen and Tong1, Definition 2.4]. Recently, Schremmer informed the author that there is an upcoming work with He and Viehmann which also aims at generalizing the fully Hodge–Newton decomposable case. For a pair
$(G,\mu )$
is weakly fully Hodge–Newton decomposable [Reference Chen and Tong1, Definition 2.4]. Recently, Schremmer informed the author that there is an upcoming work with He and Viehmann which also aims at generalizing the fully Hodge–Newton decomposable case. For a pair
![]() $(G,\mu )$
, they define a nonnegative rational number
$(G,\mu )$
, they define a nonnegative rational number
![]() $\mathrm {depth}(G,\mu )$
. Then it is known that
$\mathrm {depth}(G,\mu )$
. Then it is known that
![]() $(G,\mu )$
is fully Hodge–Newton decomposable if and only if
$(G,\mu )$
is fully Hodge–Newton decomposable if and only if
![]() $\mathrm {depth}(G,\mu )\le 1$
(cf. [Reference Görtz, He and Nie13, Definition 3.2]). They classified the cases where
$\mathrm {depth}(G,\mu )\le 1$
(cf. [Reference Görtz, He and Nie13, Definition 3.2]). They classified the cases where
![]() $1<\mathrm {depth}(G,\mu )<2$
. The classifications of these works have similarities, and most cocharacters in Theorem A appear in these works (see also [Reference Shimada38, Section 1]). Moreover, the nice stratification in [Reference Shimada38] suggests that these cases would be new cases such that
$1<\mathrm {depth}(G,\mu )<2$
. The classifications of these works have similarities, and most cocharacters in Theorem A appear in these works (see also [Reference Shimada38, Section 1]). Moreover, the nice stratification in [Reference Shimada38] suggests that these cases would be new cases such that
![]() $X_{\preceq \mu }(\tau _\mu )$
admits a simple description (as already predicted in [Reference Chen and Tong1, Remark 2.16]). Thus, for general G, both (i) and (ii) are also reasonable conditions to find such simple cases which would have many applications as the Bruhat-Tits stratification.
$X_{\preceq \mu }(\tau _\mu )$
admits a simple description (as already predicted in [Reference Chen and Tong1, Remark 2.16]). Thus, for general G, both (i) and (ii) are also reasonable conditions to find such simple cases which would have many applications as the Bruhat-Tits stratification.
It is worth mentioning that there are some other
![]() $(G,\mu )$
such that the corresponding basic affine Deligne–Lusztig variety admits a certain simple description. For example, the works by Fox-Imai [Reference Fox and Imai7] (see also [Reference Fox, Howard and Imai6]) and Trentin [Reference Trentin41] are such cases. Interestingly, both cases have
$(G,\mu )$
such that the corresponding basic affine Deligne–Lusztig variety admits a certain simple description. For example, the works by Fox-Imai [Reference Fox and Imai7] (see also [Reference Fox, Howard and Imai6]) and Trentin [Reference Trentin41] are such cases. Interestingly, both cases have
![]() $\mathrm {depth}(G,\mu )=2$
. It is also interesting to compare the
$\mathrm {depth}(G,\mu )=2$
. It is also interesting to compare the
![]() $\mathbb J$
-stratification and the Ekedahl–Oort stratification in these cases because the result will be useful to find new simple cases.
$\mathbb J$
-stratification and the Ekedahl–Oort stratification in these cases because the result will be useful to find new simple cases.
Cyclic semi-modules are certain simple elements in the set of extended semi-modules. It is easy to see that if there exists a noncyclic semi-module for
![]() $\mu $
, then the semi-module stratification of
$\mu $
, then the semi-module stratification of
![]() $X_\mu (\tau _\mu )$
never gives a refinement of the Ekedahl–Oort stratification (Corollary 3.10). Along the way of proving Theorem A, we also prove the following classification theorem, which ensures that there exists a noncyclic semi-module in many cases.
$X_\mu (\tau _\mu )$
never gives a refinement of the Ekedahl–Oort stratification (Corollary 3.10). Along the way of proving Theorem A, we also prove the following classification theorem, which ensures that there exists a noncyclic semi-module in many cases.
Theorem B (See Theorem 4.17)
Every top extended semi-module (the semi-module whose corresponding stratum is top dimensional) for
![]() $\mu $
is cyclic if and only if
$\mu $
is cyclic if and only if
![]() $\mu $
has one of the following forms modulo
$\mu $
has one of the following forms modulo
![]() $\mathbb Z\omega _n$
:
$\mathbb Z\omega _n$
:
-
(i)
 $\omega _i$
with
$\omega _i$
with
 $1\le i\le n-1$
such that i is coprime to n.
$1\le i\le n-1$
such that i is coprime to n. -
(ii)
 $\omega _1+\omega _i$
or
$\omega _1+\omega _i$
or
 $\omega _{n-1}+\omega _{n-i}$
with
$\omega _{n-1}+\omega _{n-i}$
with
 $1\le i\le n-1$
such that
$1\le i\le n-1$
such that
 $i+1$
is coprime to n.
$i+1$
is coprime to n. -
(iii)
 $(nr+i)\omega _1$
or
$(nr+i)\omega _1$
or
 $(nr+i)\omega _{n-1}$
with
$(nr+i)\omega _{n-1}$
with
 $r\geq 0$
and
$r\geq 0$
and
 $1\le i\le n-1$
such that i is coprime to n.
$1\le i\le n-1$
such that i is coprime to n. -
(iv)
 $(nr+i-j)\omega _1+\omega _j$
or
$(nr+i-j)\omega _1+\omega _j$
or
 $(nr+i-j)\omega _{n-1}+\omega _{n-j}$
with
$(nr+i-j)\omega _{n-1}+\omega _{n-j}$
with
 $r\geq 1$
,
$r\geq 1$
,
 $2\le j\le n-1$
and
$2\le j\le n-1$
and
 $1\le i\le n-1$
such that i is coprime to n.
$1\le i\le n-1$
such that i is coprime to n.
The key ingredient of the proof of Theorem B is an explicit construction of top extended semi-modules from crystal bases via the natural map in the Chen-Zhu conjecture, which was established in [Reference Shimada40] by the author. This method is a completely new way of studying the affine Deligne–Lusztig varieties. Since the Chen-Zhu conjecture holds for arbitrary G, it is an interesting question in general to investigate the affine Deligne–Lusztig varieties by crystal bases.
The paper is organized as follows. In Section 2, we introduce the affine Deligne–Lusztig variety and stratifications of it. We also recall the length positive elements and the non-emptiness criterion of the affine Deligne–Lusztig variety in the affine flag variety. In Section 3 and Section 4, we recollect known results on semi-modules and crystal bases respectively. Also in Section 4, we prove Theorem B using combinatorics on Young tableaux. In Sections 5 and 6, we examine the semi-module stratification and the Ekedahl–Oort stratification respectively by an explicit calculation of semi-modules and elements in
![]() ${^S\mathrm {Adm}}(\mu )$
. In particular, using the non-emptiness criterion mentioned above, we show that Theorem A (ii) does not hold for many
${^S\mathrm {Adm}}(\mu )$
. In particular, using the non-emptiness criterion mentioned above, we show that Theorem A (ii) does not hold for many
![]() $\mu $
. Finally, in Section 7, we prove the main theorem, combining Theorem B and the results in Section 5 and Section 6.
$\mu $
. Finally, in Section 7, we prove the main theorem, combining Theorem B and the results in Section 5 and Section 6.
2 Preliminaries
Keep the notations in Section 1.
2.1 Notation
Let
![]() $\Phi =\Phi (G,T)$
denote the set of roots of T in G. We denote by
$\Phi =\Phi (G,T)$
denote the set of roots of T in G. We denote by
![]() $\Phi _+$
(resp.
$\Phi _+$
(resp.
![]() $\Phi _-$
) the set of positive (resp. negative) roots distinguished by B. Let
$\Phi _-$
) the set of positive (resp. negative) roots distinguished by B. Let
![]() $\Delta $
be the set of simple roots and
$\Delta $
be the set of simple roots and
![]() $\Delta ^\vee $
be the corresponding set of simple coroots. Let
$\Delta ^\vee $
be the corresponding set of simple coroots. Let
![]() $X_*(T)$
be the set of cocharacters, and let
$X_*(T)$
be the set of cocharacters, and let
![]() $X_*(T)_+$
be the set of dominant cocharacters.
$X_*(T)_+$
be the set of dominant cocharacters.
The Iwahori-Weyl group
![]() $\tilde W$
is defined as the quotient
$\tilde W$
is defined as the quotient
![]() $N_{G(L)}T(L)/T(\mathcal O)$
. This can be identified with the semi-direct product
$N_{G(L)}T(L)/T(\mathcal O)$
. This can be identified with the semi-direct product
![]() $W_0\ltimes X_{*}(T)$
, where
$W_0\ltimes X_{*}(T)$
, where
![]() $W_0$
is the finite Weyl group of G. We denote the projection
$W_0$
is the finite Weyl group of G. We denote the projection
![]() $\tilde W\rightarrow W_0$
by p. We have a length function
$\tilde W\rightarrow W_0$
by p. We have a length function
![]() $\ell \colon \tilde W\rightarrow \mathbb Z_{\geq 0}$
given as
$\ell \colon \tilde W\rightarrow \mathbb Z_{\geq 0}$
given as
where
![]() $w_0\in W_0$
and
$w_0\in W_0$
and
![]() $\lambda \in X_*(T)$
.
$\lambda \in X_*(T)$
.
Let
![]() $S\subset W_0$
denote the subset of simple reflections, and let
$S\subset W_0$
denote the subset of simple reflections, and let
![]() $\tilde S\subset \tilde W$
denote the subset of simple affine reflections. We often identify
$\tilde S\subset \tilde W$
denote the subset of simple affine reflections. We often identify
![]() $\Delta $
and S. The affine Weyl group
$\Delta $
and S. The affine Weyl group
![]() $W_a$
is the subgroup of
$W_a$
is the subgroup of
![]() $\tilde W$
generated by
$\tilde W$
generated by
![]() $\tilde S$
. Then we can write the Iwahori-Weyl group as a semi-direct product
$\tilde S$
. Then we can write the Iwahori-Weyl group as a semi-direct product
![]() $\tilde W=W_a\rtimes \Omega $
, where
$\tilde W=W_a\rtimes \Omega $
, where
![]() $\Omega \subset \tilde W$
is the subgroup of length
$\Omega \subset \tilde W$
is the subgroup of length
![]() $0$
elements. Moreover,
$0$
elements. Moreover,
![]() $(W_a, \tilde S)$
is a Coxeter system. We denote by
$(W_a, \tilde S)$
is a Coxeter system. We denote by
![]() $\le $
the Bruhat order on
$\le $
the Bruhat order on
![]() $\tilde W$
. For any
$\tilde W$
. For any
![]() $J\subseteq \tilde S$
, let
$J\subseteq \tilde S$
, let
![]() $^J\tilde W$
be the set of minimal length representatives for the cosets in
$^J\tilde W$
be the set of minimal length representatives for the cosets in
![]() $W_J\backslash \tilde W$
, where
$W_J\backslash \tilde W$
, where
![]() $W_J$
denotes the subgroup of
$W_J$
denotes the subgroup of
![]() $\tilde W$
generated by J.
$\tilde W$
generated by J.
Let
![]() $w\in \tilde W$
. There exists a positive integer k such that
$w\in \tilde W$
. There exists a positive integer k such that
![]() $w^k=\varpi ^\lambda $
for some
$w^k=\varpi ^\lambda $
for some
![]() $\lambda \in X_*(T)$
. We set
$\lambda \in X_*(T)$
. We set
![]() $\nu _w=\lambda /k \in X_*(T)_{\mathbb Q}$
. This is independent of the choice of k.
$\nu _w=\lambda /k \in X_*(T)_{\mathbb Q}$
. This is independent of the choice of k.
For
![]() $w\in W_a$
, we denote by
$w\in W_a$
, we denote by
![]() $\operatorname {\mathrm {supp}}(w)\subseteq \tilde S$
the set of simple affine reflections occurring in every (equivalently, some) reduced expression of w. Note that
$\operatorname {\mathrm {supp}}(w)\subseteq \tilde S$
the set of simple affine reflections occurring in every (equivalently, some) reduced expression of w. Note that
![]() $\tau \in \Omega $
acts on
$\tau \in \Omega $
acts on
![]() $\tilde S$
by conjugation. We define the
$\tilde S$
by conjugation. We define the
![]() $\sigma $
-support
$\sigma $
-support
![]() $\operatorname {\mathrm {supp}}_\sigma (w\tau )$
of
$\operatorname {\mathrm {supp}}_\sigma (w\tau )$
of
![]() $w\tau $
as the smallest
$w\tau $
as the smallest
![]() $\tau \sigma $
-stable subset of
$\tau \sigma $
-stable subset of
![]() $\tilde S$
which contains
$\tilde S$
which contains
![]() $\operatorname {\mathrm {supp}}(w)$
.
$\operatorname {\mathrm {supp}}(w)$
.
For
![]() $w,w'\in \tilde W$
and
$w,w'\in \tilde W$
and
![]() $s\in \tilde S$
, we write
$s\in \tilde S$
, we write
![]() $w{\xrightarrow {s}}_\sigma w'$
if
$w{\xrightarrow {s}}_\sigma w'$
if
![]() $w'=sw\sigma (s)$
and
$w'=sw\sigma (s)$
and
![]() $\ell (w')\le \ell (w)$
. We write
$\ell (w')\le \ell (w)$
. We write
![]() $w\rightarrow _\sigma w'$
if there is a sequence
$w\rightarrow _\sigma w'$
if there is a sequence
![]() $w=w_0,w_1,\ldots , w_k=w'$
of elements in
$w=w_0,w_1,\ldots , w_k=w'$
of elements in
![]() $\tilde W$
such that for any i,
$\tilde W$
such that for any i,
![]() $w_{i-1}{\xrightarrow {s_i}}_\sigma w_i$
for some
$w_{i-1}{\xrightarrow {s_i}}_\sigma w_i$
for some
![]() $s_i\in S$
. If
$s_i\in S$
. If
![]() $w\rightarrow _\sigma w'$
and
$w\rightarrow _\sigma w'$
and
![]() $w'\rightarrow _\sigma w$
, we write
$w'\rightarrow _\sigma w$
, we write
![]() $w\approx _\sigma w'$
.
$w\approx _\sigma w'$
.
For
![]() $\alpha \in \Phi $
, let
$\alpha \in \Phi $
, let
![]() $U_\alpha \subseteq G$
denote the corresponding root subgroup. We set
$U_\alpha \subseteq G$
denote the corresponding root subgroup. We set
which is called the standard Iwahori subgroup associated to the triple
![]() $T\subset B\subset G$
.
$T\subset B\subset G$
.
In the case
![]() $G=\operatorname {\mathrm {GL}}_n$
, we will use the following description. Let T be the torus of diagonal matrices, and we choose the subgroup of upper triangular matrices B as Borel subgroup. Let
$G=\operatorname {\mathrm {GL}}_n$
, we will use the following description. Let T be the torus of diagonal matrices, and we choose the subgroup of upper triangular matrices B as Borel subgroup. Let
![]() $\chi _{ij}$
be the character
$\chi _{ij}$
be the character
![]() $T\rightarrow \mathbb G_m$
defined by
$T\rightarrow \mathbb G_m$
defined by
![]() $\mathrm {diag}(t_1,t_2,\ldots , t_n)\mapsto t_i{t_j}^{-1}$
. Then we have
$\mathrm {diag}(t_1,t_2,\ldots , t_n)\mapsto t_i{t_j}^{-1}$
. Then we have
![]() $\Phi =\{\chi _{ij}\mid i\neq j\}$
,
$\Phi =\{\chi _{ij}\mid i\neq j\}$
,
![]() $\Phi _+=\{\chi _{ij}\mid i< j\}$
,
$\Phi _+=\{\chi _{ij}\mid i< j\}$
,
![]() $\Phi _-=\{\chi _{ij}\mid i> j\}$
and
$\Phi _-=\{\chi _{ij}\mid i> j\}$
and
![]() $\Delta =\{\chi _{i,i+1}\mid 1\le i <n\}$
. Through a natural isomorphism
$\Delta =\{\chi _{i,i+1}\mid 1\le i <n\}$
. Through a natural isomorphism
![]() $X_*(T)\cong \mathbb Z^n$
,
$X_*(T)\cong \mathbb Z^n$
,
![]() ${X_*(T)}_+$
can be identified with the set
${X_*(T)}_+$
can be identified with the set
![]() $\{(m_1,\ldots , m_n)\in \mathbb Z^n\mid m_1\geq \cdots \geq m_n\}$
. The finite Weyl group is the symmetric group of degree n. Let us write
$\{(m_1,\ldots , m_n)\in \mathbb Z^n\mid m_1\geq \cdots \geq m_n\}$
. The finite Weyl group is the symmetric group of degree n. Let us write
![]() $s_1=(1\ 2), s_2=(2\ 3), \ldots , s_{n-1}=(n-1\ n)$
. Set
$s_1=(1\ 2), s_2=(2\ 3), \ldots , s_{n-1}=(n-1\ n)$
. Set
![]() $s_0=\varpi ^{\chi _{1,n}^{\vee }}(1\ n)$
, where
$s_0=\varpi ^{\chi _{1,n}^{\vee }}(1\ n)$
, where
![]() $\chi _{1,n}$
is the unique highest root. Then
$\chi _{1,n}$
is the unique highest root. Then
![]() $S=\{s_1,s_2,\ldots , s_{n-1}\}$
and
$S=\{s_1,s_2,\ldots , s_{n-1}\}$
and
![]() $\tilde S=S\cup \{s_0\}$
. The Iwahori subgroup
$\tilde S=S\cup \{s_0\}$
. The Iwahori subgroup
![]() $I\subset K$
is the inverse image of the lower triangular matrices under the projection
$I\subset K$
is the inverse image of the lower triangular matrices under the projection
![]() $K\rightarrow G(\overline {\mathbb F}_q)$
induced by
$K\rightarrow G(\overline {\mathbb F}_q)$
induced by
![]() $\varpi \mapsto 0$
. Set
$\varpi \mapsto 0$
. Set
 $\tau ={\begin {pmatrix} 0 & \varpi \\ 1_{n-1} & 0\\ \end {pmatrix}}$
. We often regard
$\tau ={\begin {pmatrix} 0 & \varpi \\ 1_{n-1} & 0\\ \end {pmatrix}}$
. We often regard
![]() $\tau $
as an element of
$\tau $
as an element of
![]() $\tilde W$
, which is a generator of
$\tilde W$
, which is a generator of
![]() $\Omega \cong \mathbb Z$
. Note that
$\Omega \cong \mathbb Z$
. Note that
![]() $b\in \operatorname {\mathrm {GL}}_n(L)$
is superbasic if and only if
$b\in \operatorname {\mathrm {GL}}_n(L)$
is superbasic if and only if
![]() $[b]=[\tau ^m]$
in
$[b]=[\tau ^m]$
in
![]() $B(\operatorname {\mathrm {GL}}_n)$
for some m coprime to n.
$B(\operatorname {\mathrm {GL}}_n)$
for some m coprime to n.
2.2 Affine Deligne–Lusztig varieties
For
![]() $w\in \tilde W$
and
$w\in \tilde W$
and
![]() $b\in G(L)$
, the affine Deligne–Lusztig variety
$b\in G(L)$
, the affine Deligne–Lusztig variety
![]() $X_w(b)$
in the affine flag variety
$X_w(b)$
in the affine flag variety
![]() $G(L)/I$
is defined as
$G(L)/I$
is defined as
For
![]() $\mu \in X_*(T)_+$
and
$\mu \in X_*(T)_+$
and
![]() $b\in G(L)$
, the affine Deligne–Lusztig variety
$b\in G(L)$
, the affine Deligne–Lusztig variety
![]() $X_{\mu }(b)$
in the affine Grassmannian
$X_{\mu }(b)$
in the affine Grassmannian
![]() ${\mathcal {G}} r=G(L)/K$
is defined as
${\mathcal {G}} r=G(L)/K$
is defined as
The closed affine Deligne–Lusztig variety is the closed reduced
![]() $\overline {\mathbb F}_q$
-subscheme of
$\overline {\mathbb F}_q$
-subscheme of
![]() ${\mathcal {G}} r$
defined as
${\mathcal {G}} r$
defined as
Left multiplication by
![]() $g^{-1}\in G(L)$
induces an isomorphism between
$g^{-1}\in G(L)$
induces an isomorphism between
![]() $X_\mu (b)$
and
$X_\mu (b)$
and
![]() $X_\mu (g^{-1}b\sigma (g))$
. Thus, the isomorphism class of the affine Deligne–Lusztig variety only depends on the
$X_\mu (g^{-1}b\sigma (g))$
. Thus, the isomorphism class of the affine Deligne–Lusztig variety only depends on the
![]() $\sigma $
-conjugacy class of b. Moreover, we have
$\sigma $
-conjugacy class of b. Moreover, we have
![]() $X_\mu (b)=X_{\mu +\lambda }(\varpi ^{\lambda }b)$
for each central
$X_\mu (b)=X_{\mu +\lambda }(\varpi ^{\lambda }b)$
for each central
![]() $\lambda \in X_*(T)$
.
$\lambda \in X_*(T)$
.
The admissible subset of
![]() $\tilde W$
associated to
$\tilde W$
associated to
![]() $\mu $
is defined as
$\mu $
is defined as
Note that
![]() $\operatorname {\mathrm {Adm}}(\mu ')\subseteq \operatorname {\mathrm {Adm}}(\mu )$
if
$\operatorname {\mathrm {Adm}}(\mu ')\subseteq \operatorname {\mathrm {Adm}}(\mu )$
if
![]() $\mu '\preceq \mu $
. Indeed if
$\mu '\preceq \mu $
. Indeed if
![]() $w\le \varpi ^{w_0\mu '}$
and
$w\le \varpi ^{w_0\mu '}$
and
![]() $\mu '\preceq \mu $
, then
$\mu '\preceq \mu $
, then
![]() $w\le \varpi ^{w_0\mu }$
by [Reference Haines16, Lemma 4.5]. Set
$w\le \varpi ^{w_0\mu }$
by [Reference Haines16, Lemma 4.5]. Set
![]() ${^S\mathrm {Adm}}(\mu )=\operatorname {\mathrm {Adm}}(\mu )\cap {^S\tilde W}$
. Then by [Reference Görtz and He11, Theorem 3.2.1] (see also [Reference Görtz, He and Rapoport15, Section 2.5]), we have
${^S\mathrm {Adm}}(\mu )=\operatorname {\mathrm {Adm}}(\mu )\cap {^S\tilde W}$
. Then by [Reference Görtz and He11, Theorem 3.2.1] (see also [Reference Görtz, He and Rapoport15, Section 2.5]), we have
where
![]() $\pi \colon G(L)/I\rightarrow G(L)/K$
is the projection. This is the so-called Ekedahl–Oort stratification.
$\pi \colon G(L)/I\rightarrow G(L)/K$
is the projection. This is the so-called Ekedahl–Oort stratification.
For any
![]() $w\in {^S\tilde W}$
, set
$w\in {^S\tilde W}$
, set
Lemma 2.1 Let
![]() $\varpi ^\mu y\in {^S\tilde W}$
with
$\varpi ^\mu y\in {^S\tilde W}$
with
![]() $\mu $
dominant and
$\mu $
dominant and
![]() $y\in W_0$
. Assume that
$y\in W_0$
. Assume that
![]() $Z(\varpi ^\mu y)=\{1\}$
. Then the projection map
$Z(\varpi ^\mu y)=\{1\}$
. Then the projection map
![]() $\pi \colon X_{\varpi ^\mu y}(b)\rightarrow X_\mu (b)$
is injective.
$\pi \colon X_{\varpi ^\mu y}(b)\rightarrow X_\mu (b)$
is injective.
Proof The proof is similar to [Reference He, Nie and Yu23, Lemma 5.4]. We may assume that
![]() $X_{\varpi ^\mu y}(b)\neq \emptyset $
. Let
$X_{\varpi ^\mu y}(b)\neq \emptyset $
. Let
![]() $gI,g'I\in X_{\varpi ^\mu y}(b)$
such that
$gI,g'I\in X_{\varpi ^\mu y}(b)$
such that
![]() $\pi (gI)=\pi (g'I)$
. Then
$\pi (gI)=\pi (g'I)$
. Then
![]() $g^{\prime -1}g\in K$
and hence
$g^{\prime -1}g\in K$
and hence
![]() $g^{\prime -1}g\in IxI$
for some
$g^{\prime -1}g\in IxI$
for some
![]() $x\in W_0$
. Since
$x\in W_0$
. Since
![]() $(g^{\prime -1}g)(g^{-1}b\sigma (g))=(g^{\prime -1}b\sigma (g'))(\sigma (g^{\prime -1}g))$
, we have
$(g^{\prime -1}g)(g^{-1}b\sigma (g))=(g^{\prime -1}b\sigma (g'))(\sigma (g^{\prime -1}g))$
, we have
![]() $(IxI)(I\varpi ^\mu yI)\cap (I\varpi ^\mu yI)(I\sigma (x)I)\neq \emptyset $
. Note that
$(IxI)(I\varpi ^\mu yI)\cap (I\varpi ^\mu yI)(I\sigma (x)I)\neq \emptyset $
. Note that
![]() $(IxI)(I\varpi ^\mu yI)=Ix \varpi ^\mu yI$
because
$(IxI)(I\varpi ^\mu yI)=Ix \varpi ^\mu yI$
because
![]() $\varpi ^\mu y\in {^S\tilde W}$
. This implies that
$\varpi ^\mu y\in {^S\tilde W}$
. This implies that
![]() $x\varpi ^\mu y=\varpi ^\mu y \sigma (x)$
. By our assumption, we must have
$x\varpi ^\mu y=\varpi ^\mu y \sigma (x)$
. By our assumption, we must have
![]() $x=1$
and hence
$x=1$
and hence
![]() $g^{\prime -1}g\in I$
as desired.
$g^{\prime -1}g\in I$
as desired.
Example 2.2 Let
![]() $G=\operatorname {\mathrm {GL}}_n$
and let
$G=\operatorname {\mathrm {GL}}_n$
and let
![]() $\varpi ^\mu y\in {^S\tilde W}$
with
$\varpi ^\mu y\in {^S\tilde W}$
with
![]() $\mu $
dominant and
$\mu $
dominant and
![]() $y\in W_0$
. If y is an n-cycle and
$y\in W_0$
. If y is an n-cycle and
![]() $\{s_1,s_{n-1}\}\nsubseteq Z(\varpi ^\mu )$
, then we have
$\{s_1,s_{n-1}\}\nsubseteq Z(\varpi ^\mu )$
, then we have
![]() $Z(\varpi ^\mu y)=\{1\}$
. Indeed, for any
$Z(\varpi ^\mu y)=\{1\}$
. Indeed, for any
![]() $x\in W_0$
,
$x\in W_0$
,
![]() $x\varpi ^\mu y=\varpi ^\mu y x$
implies that
$x\varpi ^\mu y=\varpi ^\mu y x$
implies that
![]() $xyx^{-1}=y$
and
$xyx^{-1}=y$
and
![]() $x\in Z(\varpi ^\mu )$
. Thus,
$x\in Z(\varpi ^\mu )$
. Thus,
![]() $x=y^k$
for some
$x=y^k$
for some
![]() $0\le k\le n-1$
and
$0\le k\le n-1$
and
![]() $y^k\mu =\mu $
. Since
$y^k\mu =\mu $
. Since
![]() $\{s_1,s_{n-1}\}\nsubseteq Z(\varpi ^\mu )$
, we must have
$\{s_1,s_{n-1}\}\nsubseteq Z(\varpi ^\mu )$
, we must have
![]() $k=0$
.
$k=0$
.
2.3 Deligne–Lusztig reduction method
The following Deligne–Lusztig reduction method was established in [Reference Görtz and He10, Corollary 2.5.3].
Proposition 2.3 Let
![]() $w\in \tilde W$
and let
$w\in \tilde W$
and let
![]() $s\in \tilde S$
be a simple affine reflection. If
$s\in \tilde S$
be a simple affine reflection. If
![]() $\operatorname {\mathrm {ch}}(F)>0$
, then the following two statements hold for any
$\operatorname {\mathrm {ch}}(F)>0$
, then the following two statements hold for any
![]() $b\in G(L)$
.
$b\in G(L)$
.
-
(i) If
 $\ell (sw\sigma (s))=\ell (w)$
, then there exists a
$\ell (sw\sigma (s))=\ell (w)$
, then there exists a
 $J_b(F)$
-equivariant universal homeomorphism
$J_b(F)$
-equivariant universal homeomorphism
 $X_w(b)\rightarrow X_{sw\sigma (s)}(b)$
.
$X_w(b)\rightarrow X_{sw\sigma (s)}(b)$
. -
(ii) If
 $\ell (sw\sigma (s))=\ell (w)-2$
, then there exists a decomposition
$\ell (sw\sigma (s))=\ell (w)-2$
, then there exists a decomposition
 $X_w(b)=X_1\sqcup X_2$
such that
$X_w(b)=X_1\sqcup X_2$
such that-
•
 $X_1$
is open and there exists a
$X_1$
is open and there exists a
 $J_b(F)$
-equivariant morphism
$J_b(F)$
-equivariant morphism
 $X_1\rightarrow X_{sw}(b)$
, which is the composition of a Zariski-locally trivial
$X_1\rightarrow X_{sw}(b)$
, which is the composition of a Zariski-locally trivial
 $\mathbb G_m$
-bundle and a universal homeomorphism.
$\mathbb G_m$
-bundle and a universal homeomorphism. -
•
 $X_2$
is closed and there exists a
$X_2$
is closed and there exists a
 $J_b(F)$
-equivariant morphism
$J_b(F)$
-equivariant morphism
 $X_2\rightarrow X_{sw\sigma (s)}(b)$
, which is the composition of a Zariski-locally trivial
$X_2\rightarrow X_{sw\sigma (s)}(b)$
, which is the composition of a Zariski-locally trivial
 $\mathbb A^1$
-bundle and a universal homeomorphism.
$\mathbb A^1$
-bundle and a universal homeomorphism.
If
 $\operatorname {\mathrm {ch}}(F)=0$
, then the above statements still hold by replacing
$\operatorname {\mathrm {ch}}(F)=0$
, then the above statements still hold by replacing
 $\mathbb A^1$
and
$\mathbb A^1$
and
 $\mathbb G_m$
by
$\mathbb G_m$
by
 $\mathbb A^{1,\operatorname {\mathrm {pfn}}}$
and
$\mathbb A^{1,\operatorname {\mathrm {pfn}}}$
and
 $\mathbb G_m^{\operatorname {\mathrm {pfn}}}$
respectively.
$\mathbb G_m^{\operatorname {\mathrm {pfn}}}$
respectively. -
The following result is proved in [Reference He and Nie22, Theorem 2.10], which allows us to reduce the study of
![]() $X_w(b)$
for any w, via the Deligne–Lusztig reduction method, to the study of
$X_w(b)$
for any w, via the Deligne–Lusztig reduction method, to the study of
![]() $X_w(b)$
for w of minimal length in its
$X_w(b)$
for w of minimal length in its
![]() $\sigma $
-conjugacy class.
$\sigma $
-conjugacy class.
Theorem 2.4 For each
![]() $w\in \tilde W$
, there exists an element
$w\in \tilde W$
, there exists an element
![]() $w'$
which is of minimal length inside its
$w'$
which is of minimal length inside its
![]() $\sigma $
-conjugacy class such that
$\sigma $
-conjugacy class such that
![]() $w\rightarrow _\sigma w'$
.
$w\rightarrow _\sigma w'$
.
Following [Reference He, Nie and Yu23, Section 3.4], we construct the reduction trees for w by induction on
![]() $\ell (w)$
.
$\ell (w)$
.
The vertices of the trees are elements of
![]() $\tilde W$
. We write
$\tilde W$
. We write
![]() $x\rightharpoonup y$
if
$x\rightharpoonup y$
if
![]() $x,y\in \tilde W$
and there exists
$x,y\in \tilde W$
and there exists
![]() $x'\in \tilde W$
and
$x'\in \tilde W$
and
![]() $s\in \tilde S$
such that
$s\in \tilde S$
such that
![]() $x\approx _\sigma x'$
,
$x\approx _\sigma x'$
,
![]() $\ell (sx'\sigma (s))=\ell (x')-2$
and
$\ell (sx'\sigma (s))=\ell (x')-2$
and
![]() $y\in \{sx', sx'\sigma (s)\}$
. These are the (oriented) edges of the trees. A reduction tree of w is a tree with these vertices and edges whose unique starting point is w and whose end points are of minimal length in its
$y\in \{sx', sx'\sigma (s)\}$
. These are the (oriented) edges of the trees. A reduction tree of w is a tree with these vertices and edges whose unique starting point is w and whose end points are of minimal length in its
![]() $\sigma $
-conjugacy class of
$\sigma $
-conjugacy class of
![]() $\tilde W$
.
$\tilde W$
.
The existence of a (not necessarily unique) reduction tree of w can be proved as follows. If w is of minimal length in its
![]() $\sigma $
-conjugacy class of
$\sigma $
-conjugacy class of
![]() $\tilde W$
, then the reduction tree for w consists of a single vertex w and no edges. Assume that w is not of minimal length and that a reduction tree is given for any
$\tilde W$
, then the reduction tree for w consists of a single vertex w and no edges. Assume that w is not of minimal length and that a reduction tree is given for any
![]() $z\in \tilde W$
with
$z\in \tilde W$
with
![]() $\ell (z)<\ell (w)$
. By Theorem 2.4, there exist
$\ell (z)<\ell (w)$
. By Theorem 2.4, there exist
![]() $w'$
and
$w'$
and
![]() $s\in \tilde S$
with
$s\in \tilde S$
with
![]() $w\approx _\sigma w'$
and
$w\approx _\sigma w'$
and
![]() $\ell (sw'\sigma (s))=\ell (w')-2$
. By our assumption, there exist reduction trees of
$\ell (sw'\sigma (s))=\ell (w')-2$
. By our assumption, there exist reduction trees of
![]() $sw'$
and
$sw'$
and
![]() $sw'\sigma (s)$
. Then a reduction tree of w consists of the given reduction trees of
$sw'\sigma (s)$
. Then a reduction tree of w consists of the given reduction trees of
![]() $sw'$
and
$sw'$
and
![]() $sw'\sigma (s)$
and the edges
$sw'\sigma (s)$
and the edges
![]() $w\rightharpoonup sw'$
and
$w\rightharpoonup sw'$
and
![]() $w\rightharpoonup sw'\sigma (s)$
.
$w\rightharpoonup sw'\sigma (s)$
.
Let
![]() $\mathcal T$
be a reduction tree of w. Recall that an end point of
$\mathcal T$
be a reduction tree of w. Recall that an end point of
![]() $\mathcal T$
is a vertex in
$\mathcal T$
is a vertex in
![]() $\mathcal T$
of minimal length. A reduction path in
$\mathcal T$
of minimal length. A reduction path in
![]() $\mathcal T$
is a path
$\mathcal T$
is a path
![]() $\underline p\colon w \rightharpoonup w_1\rightharpoonup \cdots \rightharpoonup w_n$
, where
$\underline p\colon w \rightharpoonup w_1\rightharpoonup \cdots \rightharpoonup w_n$
, where
![]() $w_n$
is an end point of
$w_n$
is an end point of
![]() $\mathcal T$
. Set
$\mathcal T$
. Set
![]() $\operatorname {\mathrm {end}}(\underline p)=w_n$
. We say that
$\operatorname {\mathrm {end}}(\underline p)=w_n$
. We say that
![]() $x\rightharpoonup y$
is of type I (resp. II) if
$x\rightharpoonup y$
is of type I (resp. II) if
![]() $\ell (x)-\ell (y)=1$
(resp.
$\ell (x)-\ell (y)=1$
(resp.
![]() $\ell (x)-\ell (y)=2$
). For any reduction path
$\ell (x)-\ell (y)=2$
). For any reduction path
![]() $\underline p$
, we denote by
$\underline p$
, we denote by
![]() $\ell _{I}(\underline p)$
(resp.
$\ell _{I}(\underline p)$
(resp.
![]() $\ell _{II}(\underline p)$
) the number of type I (resp. II) edges in
$\ell _{II}(\underline p)$
) the number of type I (resp. II) edges in
![]() $\underline p$
. We write
$\underline p$
. We write
![]() $X_{\underline p}$
for a locally closed subscheme of
$X_{\underline p}$
for a locally closed subscheme of
![]() $X_w(b)$
which is
$X_w(b)$
which is
![]() $J_b(F)$
-equivariant universally homeomorphic to an iterated fibration of type
$J_b(F)$
-equivariant universally homeomorphic to an iterated fibration of type
![]() $(\ell _{I}(\underline p),\ell _{II}(\underline p))$
over
$(\ell _{I}(\underline p),\ell _{II}(\underline p))$
over
![]() $X_{\operatorname {\mathrm {end}}(\underline p)}(b)$
.
$X_{\operatorname {\mathrm {end}}(\underline p)}(b)$
.
Let
![]() $B(\tilde W,\sigma )$
be the set of
$B(\tilde W,\sigma )$
be the set of
![]() $\sigma $
-conjugacy classes in
$\sigma $
-conjugacy classes in
![]() $\tilde W$
. Let
$\tilde W$
. Let
![]() $\Psi \colon B(\tilde W,\sigma )\rightarrow B(G)$
be the map sending
$\Psi \colon B(\tilde W,\sigma )\rightarrow B(G)$
be the map sending
![]() $[w]\in B(\tilde W,\sigma )$
to
$[w]\in B(\tilde W,\sigma )$
to
![]() $[\dot w]\in B(G)$
, where
$[\dot w]\in B(G)$
, where
![]() $\dot w\in G(L)$
is a lift of w. It is known that this map is well-defined and surjective, see [Reference He21, Theorem 3.7]. By [Reference He, Nie and Yu23, Proposition 3.9], we have the following description of
$\dot w\in G(L)$
is a lift of w. It is known that this map is well-defined and surjective, see [Reference He21, Theorem 3.7]. By [Reference He, Nie and Yu23, Proposition 3.9], we have the following description of
![]() $X_w(b)$
.
$X_w(b)$
.
Proposition 2.5 Let
![]() $w\in \tilde W$
and
$w\in \tilde W$
and
![]() $\mathcal T$
be a reduction tree of w. For any
$\mathcal T$
be a reduction tree of w. For any
![]() $b\in G(L)$
, there exists a decomposition
$b\in G(L)$
, there exists a decomposition
 $$ \begin{align*}X_w(b)=\bigsqcup_{\substack{\underline p\ \text{is a reduction path in}\ \mathcal T;\\ \Psi(\operatorname{\mathrm{end}}(\underline p))=[b]}}X_{\underline p}.\end{align*} $$
$$ \begin{align*}X_w(b)=\bigsqcup_{\substack{\underline p\ \text{is a reduction path in}\ \mathcal T;\\ \Psi(\operatorname{\mathrm{end}}(\underline p))=[b]}}X_{\underline p}.\end{align*} $$
In the case that
![]() $G=\operatorname {\mathrm {GL}}_n$
and
$G=\operatorname {\mathrm {GL}}_n$
and
![]() $b=\tau ^m$
with m coprime to n, we can count the number of top irreducible components and rational points of
$b=\tau ^m$
with m coprime to n, we can count the number of top irreducible components and rational points of
![]() $X_w(b)^0=\{gI\in X_w(b)\mid \kappa (g)=v_L(\det (g))=0\}$
using the reduction tree for w. By [Reference He and Nie22, Proposition 3.5], the
$X_w(b)^0=\{gI\in X_w(b)\mid \kappa (g)=v_L(\det (g))=0\}$
using the reduction tree for w. By [Reference He and Nie22, Proposition 3.5], the
![]() $\sigma $
-conjugacy class of
$\sigma $
-conjugacy class of
![]() $\tau ^m$
in
$\tau ^m$
in
![]() $\tilde W$
is the unique element in
$\tilde W$
is the unique element in
![]() $B(\tilde W,\sigma )$
which maps to
$B(\tilde W,\sigma )$
which maps to
![]() $[\tau ^m]\in B(G)$
under
$[\tau ^m]\in B(G)$
under
![]() $\Psi $
. Note also that
$\Psi $
. Note also that
![]() $\tau ^m$
is the unique minimal length element in its
$\tau ^m$
is the unique minimal length element in its
![]() $\sigma $
-conjugacy class. We define a polynomial as
$\sigma $
-conjugacy class. We define a polynomial as
where
![]() $\underline p$
runs over all the reduction paths in
$\underline p$
runs over all the reduction paths in
![]() $\mathcal T$
with
$\mathcal T$
with
![]() $\operatorname {\mathrm {end}}(\underline p)=\tau ^m$
.
$\operatorname {\mathrm {end}}(\underline p)=\tau ^m$
.
Proposition 2.6 Assume that
![]() $G=\operatorname {\mathrm {GL}}_n$
and
$G=\operatorname {\mathrm {GL}}_n$
and
![]() $b=\tau ^m$
with m coprime to n. Let
$b=\tau ^m$
with m coprime to n. Let
![]() $w\in \tilde W$
and let
$w\in \tilde W$
and let
![]() $\mathcal T$
be a reduction tree of w. Then the number of top irreducible components of
$\mathcal T$
be a reduction tree of w. Then the number of top irreducible components of
![]() $X_w(b)^0$
is equal to the leading coefficient of
$X_w(b)^0$
is equal to the leading coefficient of
![]() $F_{w,b}$
(as a polynomial in
$F_{w,b}$
(as a polynomial in
![]() $\mathbf q-1$
). Moreover, we have
$\mathbf q-1$
). Moreover, we have
Proof Note that each
![]() $J_b(F)$
-orbit of an irreducible component of
$J_b(F)$
-orbit of an irreducible component of
![]() $X_w(b)$
can be represented by an irreducible component of
$X_w(b)$
can be represented by an irreducible component of
![]() $X_w(b)^0$
. Moreover, it is known that the stabilizer in
$X_w(b)^0$
. Moreover, it is known that the stabilizer in
![]() $J_b(F)$
is a parahoric subgroup (cf. [Reference Zhou and Zhu47, Proposition 3.1.4]), i.e.,
$J_b(F)$
is a parahoric subgroup (cf. [Reference Zhou and Zhu47, Proposition 3.1.4]), i.e.,
![]() $J_b(F)\cap I=\{g\in J_b(F)\mid \kappa (g)=0\}$
. Then the statement follows from [Reference He, Nie and Yu23, Theorem 3.4 and Proposition 3.5] and [Reference He and Zhou24, Corollary 4.4].
$J_b(F)\cap I=\{g\in J_b(F)\mid \kappa (g)=0\}$
. Then the statement follows from [Reference He, Nie and Yu23, Theorem 3.4 and Proposition 3.5] and [Reference He and Zhou24, Corollary 4.4].
Remark 2.7 The polynomials
![]() $F_{w,b}$
are called class polynomials. However, the definition above is an ad hoc one. See [Reference He, Nie and Yu23, Section 3] for the definition in general and the connection to reduction trees.
$F_{w,b}$
are called class polynomials. However, the definition above is an ad hoc one. See [Reference He, Nie and Yu23, Section 3] for the definition in general and the connection to reduction trees.
2.4 The
 $\mathbb J$
-stratification
$\mathbb J$
-stratification
For any
![]() $g,h\in G(L)$
, let
$g,h\in G(L)$
, let
![]() $\mathrm {inv}(g,h)$
denote the relative position, i.e., the unique dominant cocharacter such that
$\mathrm {inv}(g,h)$
denote the relative position, i.e., the unique dominant cocharacter such that
![]() $g^{-1}h\in K\varpi ^{\mathrm {inv}(g,h)} K$
. By definition, two elements
$g^{-1}h\in K\varpi ^{\mathrm {inv}(g,h)} K$
. By definition, two elements
![]() $gK,hK\in G(L)/K$
lie in the same
$gK,hK\in G(L)/K$
lie in the same
![]() $\mathbb J$
-stratum if and only if for all
$\mathbb J$
-stratum if and only if for all
![]() $j\in J_b(F)$
,
$j\in J_b(F)$
,
![]() $\mathrm {inv}(j,g)=\mathrm {inv}(j,h)$
. Clearly, this does not depend on the choice of
$\mathrm {inv}(j,g)=\mathrm {inv}(j,h)$
. Clearly, this does not depend on the choice of
![]() $g,h$
. By [Reference Chen and Viehmann2, Proposition 2.11], the
$g,h$
. By [Reference Chen and Viehmann2, Proposition 2.11], the
![]() $\mathbb J$
-strata are locally closed in
$\mathbb J$
-strata are locally closed in
![]() ${\mathcal {G}} r$
. By intersecting each
${\mathcal {G}} r$
. By intersecting each
![]() $\mathbb J$
-stratum with
$\mathbb J$
-stratum with
![]() $X_\mu (b)$
(resp.
$X_\mu (b)$
(resp.
![]() $X_{\preceq \mu }(b)$
), we obtain the
$X_{\preceq \mu }(b)$
), we obtain the
![]() $\mathbb J$
-stratification of
$\mathbb J$
-stratification of
![]() $X_\mu (b)$
(resp.
$X_\mu (b)$
(resp.
![]() $X_{\preceq \mu }(b)$
).
$X_{\preceq \mu }(b)$
).
As explained in [Reference Chen and Viehmann2, Remark 2.1], the
![]() $\mathbb J$
-stratification heavily depends on the choice of b in its
$\mathbb J$
-stratification heavily depends on the choice of b in its
![]() $\sigma $
-conjugacy class. So we need to fix a specific representative to compare the
$\sigma $
-conjugacy class. So we need to fix a specific representative to compare the
![]() $\mathbb J$
-stratification on
$\mathbb J$
-stratification on
![]() $X_\mu (b)$
(or
$X_\mu (b)$
(or
![]() $X_{\preceq \mu }(b)$
) to another stratification. It is pointed out in loc. cit that if
$X_{\preceq \mu }(b)$
) to another stratification. It is pointed out in loc. cit that if
![]() $[b]$
is a basic class in
$[b]$
is a basic class in
![]() $B(G, \mu )$
, then a reasonable choice of b is the unique length
$B(G, \mu )$
, then a reasonable choice of b is the unique length
![]() $0$
element
$0$
element
![]() $\tau _{\mu }$
. Also, for any
$\tau _{\mu }$
. Also, for any
![]() $w\in \tilde W$
, the
$w\in \tilde W$
, the
![]() $J_{\dot w}(F)$
-stratification is independent of the choice of a lift in
$J_{\dot w}(F)$
-stratification is independent of the choice of a lift in
![]() $G(L)$
. See [Reference Görtz9, Lemma 2.5].
$G(L)$
. See [Reference Görtz9, Lemma 2.5].
In the case where
![]() $G=\operatorname {\mathrm {GL}}_n$
and
$G=\operatorname {\mathrm {GL}}_n$
and
![]() $b=\tau ^m$
with m coprime to n, there is a group-theoretic way to describe the
$b=\tau ^m$
with m coprime to n, there is a group-theoretic way to describe the
![]() $\mathbb J$
-stratification, which we will call the semi-module stratification. Indeed, by [Reference Chen and Viehmann2, Remark 3.1 and Proposition 3.4], the
$\mathbb J$
-stratification, which we will call the semi-module stratification. Indeed, by [Reference Chen and Viehmann2, Remark 3.1 and Proposition 3.4], the
![]() $\mathbb J$
-stratification on
$\mathbb J$
-stratification on
![]() ${\mathcal {G}} r$
coincides with the stratification
${\mathcal {G}} r$
coincides with the stratification
So in this case, each
![]() $\mathbb J$
-stratum of
$\mathbb J$
-stratum of
![]() $X_\mu (b)$
(resp.
$X_\mu (b)$
(resp.
![]() $X_{\preceq \mu }(b)$
) coincides with
$X_{\preceq \mu }(b)$
) coincides with
![]() $X_\mu ^\lambda (b)$
(resp.
$X_\mu ^\lambda (b)$
(resp.
![]() $X_{\preceq \mu }^\lambda (b)$
) for some
$X_{\preceq \mu }^\lambda (b)$
) for some
![]() $\lambda \in X_*(T)$
, where
$\lambda \in X_*(T)$
, where
![]() $X_\mu ^\lambda (b)=X_\mu (b)\cap I \varpi ^\lambda K/K$
(resp.
$X_\mu ^\lambda (b)=X_\mu (b)\cap I \varpi ^\lambda K/K$
(resp.
![]() $X_{\preceq \mu }^\lambda (b)=X_{\preceq \mu }(b)\cap I \varpi ^\lambda K/K$
). Set
$X_{\preceq \mu }^\lambda (b)=X_{\preceq \mu }(b)\cap I \varpi ^\lambda K/K$
). Set
![]() $J_b(F)^0=J_b(F)\cap K=J_b(F)\cap I$
. Note that
$J_b(F)^0=J_b(F)\cap K=J_b(F)\cap I$
. Note that
![]() $\tau X_\mu ^\lambda (b)=X_\mu ^{\tau \lambda }(b)$
and
$\tau X_\mu ^\lambda (b)=X_\mu ^{\tau \lambda }(b)$
and
![]() $J_b(F)/J_b(F)^0=\{\tau ^k J_b(F)^0\mid k\in \mathbb Z\}$
. Thus,
$J_b(F)/J_b(F)^0=\{\tau ^k J_b(F)^0\mid k\in \mathbb Z\}$
. Thus,
See Section 3.1 for the precise definition of (extended) semi-modules. As we will explain in Section 3.2, the set
![]() $\{\lambda \in X_*(T)\mid X_\mu ^\lambda (b)\neq \emptyset \}$
can be regarded as semi-modules for
$\{\lambda \in X_*(T)\mid X_\mu ^\lambda (b)\neq \emptyset \}$
can be regarded as semi-modules for
![]() $\mu $
. Let
$\mu $
. Let
![]() $w_{\max }$
be the longest element in
$w_{\max }$
be the longest element in
![]() $W_0$
. Then we have
$W_0$
. Then we have
Indeed it is easy to check that the image of
![]() $X_\mu ^\lambda (b)$
under the automorphism of
$X_\mu ^\lambda (b)$
under the automorphism of
![]() ${\mathcal {G}} r$
by
${\mathcal {G}} r$
by
![]() $gK\mapsto w_{\max }^t g^{-1}K$
is
$gK\mapsto w_{\max }^t g^{-1}K$
is
![]() $X_{-w_{\max }\mu }^{-w_{\max }\lambda }(b^{-1})$
. This gives the description of “dual” semi-modules for
$X_{-w_{\max }\mu }^{-w_{\max }\lambda }(b^{-1})$
. This gives the description of “dual” semi-modules for
![]() $\mu $
.
$\mu $
.
2.5 Length positive elements
We denote by
![]() $\delta ^+$
the indicator function of the set of positive roots, i.e.,
$\delta ^+$
the indicator function of the set of positive roots, i.e.,
 $$ \begin{align*}\delta^+\colon \Phi\rightarrow \{0,1\},\quad \alpha \mapsto \begin{cases} 1 & (\alpha\in \Phi_+) \\ 0 & (\alpha\in \Phi_-). \end{cases}\end{align*} $$
$$ \begin{align*}\delta^+\colon \Phi\rightarrow \{0,1\},\quad \alpha \mapsto \begin{cases} 1 & (\alpha\in \Phi_+) \\ 0 & (\alpha\in \Phi_-). \end{cases}\end{align*} $$
Note that any element
![]() $w\in \tilde W$
can be written in a unique way as
$w\in \tilde W$
can be written in a unique way as
![]() $w=x\varpi ^\mu y$
with
$w=x\varpi ^\mu y$
with
![]() $\mu $
dominant,
$\mu $
dominant,
![]() $x,y\in W_0$
such that
$x,y\in W_0$
such that
![]() $\varpi ^\mu y\in {^S\tilde W}$
. We have
$\varpi ^\mu y\in {^S\tilde W}$
. We have
![]() $p(w)=xy$
and
$p(w)=xy$
and
![]() $\ell (w)=\ell (x)+\langle \mu , 2\rho \rangle -\ell (y)$
. We define the set of length positive elements by
$\ell (w)=\ell (x)+\langle \mu , 2\rho \rangle -\ell (y)$
. We define the set of length positive elements by
Then we always have
![]() $y^{-1}\in \operatorname {\mathrm {LP}}(w)$
. Indeed y satisfies the condition that
$y^{-1}\in \operatorname {\mathrm {LP}}(w)$
. Indeed y satisfies the condition that
![]() $\langle \alpha , \mu \rangle \geq \delta ^+(-y^{-1}\alpha )\ \text {for all} \alpha \in \Phi _+.$
Since
$\langle \alpha , \mu \rangle \geq \delta ^+(-y^{-1}\alpha )\ \text {for all} \alpha \in \Phi _+.$
Since
![]() $\delta ^+(\alpha )+\delta ^+(-\alpha )=1$
, we have
$\delta ^+(\alpha )+\delta ^+(-\alpha )=1$
, we have
Lemma 2.8 For any
![]() $w=x\varpi ^\mu y\in \tilde W$
as above, we define
$w=x\varpi ^\mu y\in \tilde W$
as above, we define
Here
![]() $\delta ^-$
denotes the indicator function of the set of negative roots. Then we have
$\delta ^-$
denotes the indicator function of the set of negative roots. Then we have
Proof Let
![]() $r\in W_0$
such that
$r\in W_0$
such that
![]() $r(\Phi _+\setminus \Phi _w)\subset \Phi _+$
. Let
$r(\Phi _+\setminus \Phi _w)\subset \Phi _+$
. Let
![]() $\alpha \in \Phi _+$
. If
$\alpha \in \Phi _+$
. If
![]() $r^{-1}\alpha \in \Phi _+$
, then we can check that
$r^{-1}\alpha \in \Phi _+$
, then we can check that
![]() $y^{-1}r^{-1}\in \operatorname {\mathrm {LP}}(w)$
similarly as the case
$y^{-1}r^{-1}\in \operatorname {\mathrm {LP}}(w)$
similarly as the case
![]() $r=1$
above. If
$r=1$
above. If
![]() $r^{-1}\alpha \in \Phi _-$
, then we must have
$r^{-1}\alpha \in \Phi _-$
, then we must have
![]() $r^{-1}\alpha \in -\Phi _w$
. Since
$r^{-1}\alpha \in -\Phi _w$
. Since
![]() $\delta ^-(-\alpha )=\delta ^+(\alpha )$
, it follows that
$\delta ^-(-\alpha )=\delta ^+(\alpha )$
, it follows that
 $$ \begin{align*} &\langle y^{-1}r^{-1}\alpha,y^{-1}\mu\rangle+\delta^+(y^{-1}r^{-1}\alpha)-\delta^+(xr^{-1}\alpha)\\ =&-(\langle -r^{-1}\alpha, \mu\rangle-\delta^-(-y^{-1}r^{-1}\alpha)+\delta^-(-xr^{-1}\alpha))=0. \end{align*} $$
$$ \begin{align*} &\langle y^{-1}r^{-1}\alpha,y^{-1}\mu\rangle+\delta^+(y^{-1}r^{-1}\alpha)-\delta^+(xr^{-1}\alpha)\\ =&-(\langle -r^{-1}\alpha, \mu\rangle-\delta^-(-y^{-1}r^{-1}\alpha)+\delta^-(-xr^{-1}\alpha))=0. \end{align*} $$
Thus,
![]() $y^{-1}r^{-1}\in \operatorname {\mathrm {LP}}(w)$
. This shows
$y^{-1}r^{-1}\in \operatorname {\mathrm {LP}}(w)$
. This shows
![]() $\{r^{-1}\in W_0\mid r(\Phi _+\setminus \Phi _w)\subset \Phi _+\}\subseteq y\operatorname {\mathrm {LP}}(w)$
.
$\{r^{-1}\in W_0\mid r(\Phi _+\setminus \Phi _w)\subset \Phi _+\}\subseteq y\operatorname {\mathrm {LP}}(w)$
.
Let
![]() $v\in \operatorname {\mathrm {LP}}(w)$
and let
$v\in \operatorname {\mathrm {LP}}(w)$
and let
![]() $\alpha \in \Phi _+$
. If
$\alpha \in \Phi _+$
. If
![]() $yv\alpha \in \Phi _-$
, then
$yv\alpha \in \Phi _-$
, then
On the other hand, by the characterization of y above, we have
Thus,
![]() $\langle -yv\alpha ,\mu \rangle -\delta ^-(-v\alpha )+\delta ^-(-xyv\alpha )=0$
and hence
$\langle -yv\alpha ,\mu \rangle -\delta ^-(-v\alpha )+\delta ^-(-xyv\alpha )=0$
and hence
![]() $yv\alpha \in -\Phi _w$
. This shows
$yv\alpha \in -\Phi _w$
. This shows
![]() $y\operatorname {\mathrm {LP}}(w)\subseteq \{r^{-1}\in W_0\mid r(\Phi _+\setminus \Phi _w)\subset \Phi _+\}$
. The proof is finished.
$y\operatorname {\mathrm {LP}}(w)\subseteq \{r^{-1}\in W_0\mid r(\Phi _+\setminus \Phi _w)\subset \Phi _+\}$
. The proof is finished.
The notion of length positive elements is defined by Schremmer [Reference Schremmer35]. The description of
![]() $\operatorname {\mathrm {LP}}(w)$
in Lemma 2.8 is due to Lim [Reference Lim30].
$\operatorname {\mathrm {LP}}(w)$
in Lemma 2.8 is due to Lim [Reference Lim30].
We say that the Dynkin diagram of G is
![]() $\sigma $
-connected if it cannot be written as a union of two proper
$\sigma $
-connected if it cannot be written as a union of two proper
![]() $\sigma $
-stable subdiagrams that are not connected to each other. The following theorem is a refinement of the non-emptiness criterion in [Reference Görtz, He and Nie12], which is conjectured by Lim [Reference Lim30] and proved by Schremmer [Reference Schremmer36, Proposition 5].
$\sigma $
-stable subdiagrams that are not connected to each other. The following theorem is a refinement of the non-emptiness criterion in [Reference Görtz, He and Nie12], which is conjectured by Lim [Reference Lim30] and proved by Schremmer [Reference Schremmer36, Proposition 5].
Theorem 2.9 Assume that the Dynkin diagram of G is
![]() $\sigma $
-connected. Let
$\sigma $
-connected. Let
![]() $b\in G(L)$
be a basic element with
$b\in G(L)$
be a basic element with
![]() $\kappa (b)=\kappa (\dot w)$
. Then
$\kappa (b)=\kappa (\dot w)$
. Then
![]() $X_w(b)=\emptyset $
if and only if both of the following two conditions are satisfied:
$X_w(b)=\emptyset $
if and only if both of the following two conditions are satisfied:
-
(i)
 $|W_{\operatorname {\mathrm {supp}}_\sigma (w)}|$
is not finite.
$|W_{\operatorname {\mathrm {supp}}_\sigma (w)}|$
is not finite. -
(ii) There exists
 $v\in \operatorname {\mathrm {LP}}(w)$
such that
$v\in \operatorname {\mathrm {LP}}(w)$
such that
 $\operatorname {\mathrm {supp}}_\sigma (\sigma ^{-1}(v)^{-1}p(w)v)\subsetneq S$
.
$\operatorname {\mathrm {supp}}_\sigma (\sigma ^{-1}(v)^{-1}p(w)v)\subsetneq S$
.
Remark 2.10 If
![]() $\kappa (b)\neq \kappa (\dot w)$
, then
$\kappa (b)\neq \kappa (\dot w)$
, then
![]() $X_w(b)=\emptyset $
.
$X_w(b)=\emptyset $
.
Remark 2.11 Let
![]() $w\in \tilde W, w_0\in W_0$
and let
$w\in \tilde W, w_0\in W_0$
and let
![]() $J\subseteq \Delta $
such that
$J\subseteq \Delta $
such that
![]() $J=\sigma (J)$
. Then we say that w is a
$J=\sigma (J)$
. Then we say that w is a
![]() $(J,w_0,\sigma )$
-alcove element if the following conditions are both satisfied:
$(J,w_0,\sigma )$
-alcove element if the following conditions are both satisfied:
-
(1)
 , and
, and -
(2) For any
 $\alpha \in w_0(\Phi _+\setminus \Phi _{J})$
,
$\alpha \in w_0(\Phi _+\setminus \Phi _{J})$
,
 $U_\alpha \cap {^wI}\subseteq U_\alpha \cap I$
, where
$U_\alpha \cap {^wI}\subseteq U_\alpha \cap I$
, where
 $\Phi _J$
denotes the root system generated by J.
$\Phi _J$
denotes the root system generated by J.
In [Reference Schremmer36, Proposition 5], the condition (ii) in Theorem 2.9 is written as
-
(ii)’ There exist
 $J\subsetneq \Delta $
and
$J\subsetneq \Delta $
and
 $w_0\in W_0$
such that w is a
$w_0\in W_0$
such that w is a
 $(J,w_0,\sigma )$
-alcove element.
$(J,w_0,\sigma )$
-alcove element.
The equivalence of (ii) and (ii)’ follows from [Reference Lim30, Lemmas 3.7 and 3.9] (see also [Reference Schremmer, Shimada and Yu37, Definition 2.3] and the comment right after it).
In the case
![]() $G=\operatorname {\mathrm {GL}}_n$
, there exists a length-preserving automorphism
$G=\operatorname {\mathrm {GL}}_n$
, there exists a length-preserving automorphism
![]() $\varsigma $
of
$\varsigma $
of
![]() $\tilde W$
defined as
$\tilde W$
defined as
Note that
![]() $\varsigma (\tau ^m)=\tau ^{-m}$
,
$\varsigma (\tau ^m)=\tau ^{-m}$
,
![]() $\varsigma (s_0)=s_0$
and
$\varsigma (s_0)=s_0$
and
![]() $\varsigma (s_i)=s_{n-i}$
for
$\varsigma (s_i)=s_{n-i}$
for
![]() $1\le i\le n-1$
. Let
$1\le i\le n-1$
. Let
![]() $w=x\varpi ^\mu y$
be as above. For any
$w=x\varpi ^\mu y$
be as above. For any
![]() $\alpha \in \Phi _+$
and
$\alpha \in \Phi _+$
and
![]() $v\in \operatorname {\mathrm {LP}}(w)$
, we have
$v\in \operatorname {\mathrm {LP}}(w)$
, we have
 $$ \begin{align*} &\langle \varsigma(v)(-w_{\max}\alpha), \varsigma(y^{-1})(-w_{\max}\mu)\rangle+\delta^+(\varsigma(v)(-w_{\max}\alpha))-\delta^+(\varsigma(xy)\varsigma(v)(-w_{\max}\alpha))\\ &=\langle v\alpha,y^{-1}\mu\rangle+\delta^+(v\alpha)-\delta^+(xyv\alpha)\geq 0. \end{align*} $$
$$ \begin{align*} &\langle \varsigma(v)(-w_{\max}\alpha), \varsigma(y^{-1})(-w_{\max}\mu)\rangle+\delta^+(\varsigma(v)(-w_{\max}\alpha))-\delta^+(\varsigma(xy)\varsigma(v)(-w_{\max}\alpha))\\ &=\langle v\alpha,y^{-1}\mu\rangle+\delta^+(v\alpha)-\delta^+(xyv\alpha)\geq 0. \end{align*} $$
Thus,
![]() $\operatorname {\mathrm {LP}}(\varsigma (w))=\varsigma (\operatorname {\mathrm {LP}}(w))=w_{\max }\operatorname {\mathrm {LP}}(w)w_{\max }^{-1}$
. In particular, there exists
$\operatorname {\mathrm {LP}}(\varsigma (w))=\varsigma (\operatorname {\mathrm {LP}}(w))=w_{\max }\operatorname {\mathrm {LP}}(w)w_{\max }^{-1}$
. In particular, there exists
![]() $v\in \operatorname {\mathrm {LP}}(w)$
such that
$v\in \operatorname {\mathrm {LP}}(w)$
such that
![]() $v^{-1}p(w)v$
is a Coxeter element if and only if the same is true for
$v^{-1}p(w)v$
is a Coxeter element if and only if the same is true for
![]() $\varsigma (w)$
and
$\varsigma (w)$
and
![]() $\operatorname {\mathrm {LP}}(\varsigma (w))$
.
$\operatorname {\mathrm {LP}}(\varsigma (w))$
.
3 Semi-modules
From now and until the end of this paper, we set
![]() $G=\operatorname {\mathrm {GL}}_n$
and
$G=\operatorname {\mathrm {GL}}_n$
and
![]() $b=\tau ^m$
with m coprime to n. For
$b=\tau ^m$
with m coprime to n. For
![]() $\mu \in X_*(T)_+$
, let
$\mu \in X_*(T)_+$
, let
![]() $\mu (i)$
denotes the i-th entry of
$\mu (i)$
denotes the i-th entry of
![]() $\mu $
. Then
$\mu $
. Then
![]() $[\tau ^m]\in B(G,\mu )$
if and only if
$[\tau ^m]\in B(G,\mu )$
if and only if
![]() $m=\mu (1)+\cdots +\mu (n)$
. We assume this from now. Also, without loss of generality, we may and will assume that
$m=\mu (1)+\cdots +\mu (n)$
. We assume this from now. Also, without loss of generality, we may and will assume that
![]() $\mu (n)=0$
. Recall that
$\mu (n)=0$
. Recall that
![]() $w_{\max }$
is the longest element in
$w_{\max }$
is the longest element in
![]() $W_0$
.
$W_0$
.
3.1 Extended semi-modules
Here we recall the definition of extended semi-modules in a combinatorial way from [Reference Viehmann42]. Note that although we choose the subgroup of upper triangular matrices B as a Borel subgroup in this paper, the fixed Borel subgroup in [Reference Viehmann42] is the subgroup of lower triangular matrices.
Definition 3.1 A semi-module for
![]() $m, n$
is a subset
$m, n$
is a subset
![]() $A\subset \mathbb Z$
that is bounded below and satisfies
$A\subset \mathbb Z$
that is bounded below and satisfies
![]() $m+A\subset A$
and
$m+A\subset A$
and
![]() $n+A\subset A$
. Set
$n+A\subset A$
. Set
![]() $\bar {A}=A\setminus (n+A)$
. The semi-module A is called normalized if
$\bar {A}=A\setminus (n+A)$
. The semi-module A is called normalized if
![]() $\sum _{a\in \bar {A}}a=\frac {n(n-1)}{2}$
.
$\sum _{a\in \bar {A}}a=\frac {n(n-1)}{2}$
.
For a semi-module A, there exists a unique
![]() $\mu '\in \mathbb N^n$
satisfying the following condition: Let
$\mu '\in \mathbb N^n$
satisfying the following condition: Let
![]() $a_0=\min \bar A$
and let inductively
$a_0=\min \bar A$
and let inductively
![]() $a_i=a_{i-1}+m-\mu '(i)n$
for
$a_i=a_{i-1}+m-\mu '(i)n$
for
![]() $i=1,\ldots , n$
. Then
$i=1,\ldots , n$
. Then
![]() $a_0=a_n$
and
$a_0=a_n$
and
![]() $\{a_0,a_1,\ldots ,a_{n-1}\}=\bar A$
. We call
$\{a_0,a_1,\ldots ,a_{n-1}\}=\bar A$
. We call
![]() $\mu '$
the type of A.
$\mu '$
the type of A.
Lemma 3.2 There is a bijection between the set of normalized semi-modules for
![]() $m,n$
and the set of possible types
$m,n$
and the set of possible types
![]() $\mu '\in \mathbb N^n$
with
$\mu '\in \mathbb N^n$
with
![]() $\nu _b\preceq w_{\max }\mu '$
.
$\nu _b\preceq w_{\max }\mu '$
.
Proof This is [Reference Viehmann42, Lemma 3.3].
Definition 3.3 An extended semi-module
![]() $(A,\varphi )$
for
$(A,\varphi )$
for
![]() $\mu \in X_*(T)_+$
is a normalized semi-module A for
$\mu \in X_*(T)_+$
is a normalized semi-module A for
![]() $m,n$
together with a function
$m,n$
together with a function
![]() $\varphi \colon \mathbb Z\rightarrow \mathbb N\cup \{-\infty \}$
satisfying the following properties:
$\varphi \colon \mathbb Z\rightarrow \mathbb N\cup \{-\infty \}$
satisfying the following properties:
-
(1)
 $\varphi (a)=-\infty $
if and only if
$\varphi (a)=-\infty $
if and only if
 $a\notin A$
.
$a\notin A$
. -
(2)
 $\varphi (a+n)\geq \varphi (a)+1$
for all
$\varphi (a+n)\geq \varphi (a)+1$
for all
 $a\in \mathbb Z$
.
$a\in \mathbb Z$
. -
(3)
 $\varphi (a)\le \max \{k\mid a+m-kn\in A\}$
for all
$\varphi (a)\le \max \{k\mid a+m-kn\in A\}$
for all
 $a\in A$
. If
$a\in A$
. If
 $b\in A$
for all
$b\in A$
for all
 $b\geq a$
, then the two sides are equal.
$b\geq a$
, then the two sides are equal. -
(4) There is a decomposition of A into disjoint union of sequences
 $a_j^1,\ldots , a_j^n$
with
$a_j^1,\ldots , a_j^n$
with
 $j\in \mathbb N$
and the following properties:
$j\in \mathbb N$
and the following properties:-
(a)
 $\varphi (a_{j+1}^l)=\varphi (a_j^l)+1$
.
$\varphi (a_{j+1}^l)=\varphi (a_j^l)+1$
. -
(b) If
 $\varphi (a_j^l+n)=\varphi (a_j^l)+1$
, then
$\varphi (a_j^l+n)=\varphi (a_j^l)+1$
, then
 $a_{j+1}^l=a_j^l+n$
. Otherwise
$a_{j+1}^l=a_j^l+n$
. Otherwise
 $a_{j+1}^l>a_j^l+n$
.
$a_{j+1}^l>a_j^l+n$
. -
(c) The n-tuple
 $(\varphi (a_0^l))$
is a permutation of
$(\varphi (a_0^l))$
is a permutation of
 $\mu $
.
$\mu $
.
-
An extended semi-module such that the equality holds in (3) for all
![]() $a\in A$
is called cyclic.
$a\in A$
is called cyclic.
For any
![]() $\lambda \in X_*(T)$
, we denote by
$\lambda \in X_*(T)$
, we denote by
![]() $\lambda _{\operatorname {\mathrm {dom}}}$
the dominant conjugate of
$\lambda _{\operatorname {\mathrm {dom}}}$
the dominant conjugate of
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $\mu '$
be the type of a semi-module for
$\mu '$
be the type of a semi-module for
![]() $m,n$
. Let
$m,n$
. Let
![]() $\varphi $
be a function such that
$\varphi $
be a function such that
![]() $(1)$
and the equation in
$(1)$
and the equation in
![]() $(3)$
hold. Then it is easy to check that
$(3)$
hold. Then it is easy to check that
![]() $(A,\varphi )$
is a cyclic semi-module for
$(A,\varphi )$
is a cyclic semi-module for
![]() $\mu ^{\prime }_{\operatorname {\mathrm {dom}}}$
. In general, the following lemma holds.
$\mu ^{\prime }_{\operatorname {\mathrm {dom}}}$
. In general, the following lemma holds.
Lemma 3.4 Let
![]() $(A,\varphi )$
be an extended semi-module for
$(A,\varphi )$
be an extended semi-module for
![]() $\mu $
and let
$\mu $
and let
![]() $\mu '$
be the type of A. Then
$\mu '$
be the type of A. Then
![]() $\mu ^{\prime }_{\operatorname {\mathrm {dom}}}\preceq \mu $
and
$\mu ^{\prime }_{\operatorname {\mathrm {dom}}}\preceq \mu $
and
![]() $(A,\varphi )$
is cyclic if and only if
$(A,\varphi )$
is cyclic if and only if
![]() $\mu '\in W_0\mu $
. In particular, if
$\mu '\in W_0\mu $
. In particular, if
![]() $\mu $
is minuscule, then all extended semi-modules for
$\mu $
is minuscule, then all extended semi-modules for
![]() $\mu $
are cyclic.
$\mu $
are cyclic.
Proof See [Reference Viehmann42, Lemma 3.6 and Corollary 3.7]. See also [Reference Hamacher17, Lemma 5.9].
Let
![]() $e_0,\ldots , e_{n-1}$
be the standard basis of
$e_0,\ldots , e_{n-1}$
be the standard basis of
![]() $L^n$
. Then the lattice
$L^n$
. Then the lattice
![]() $\mathcal O^n$
is generated by
$\mathcal O^n$
is generated by
![]() $e_0,\ldots , e_{n-1}$
. For
$e_0,\ldots , e_{n-1}$
. For
![]() $i\in \mathbb Z$
, we define
$i\in \mathbb Z$
, we define
![]() $e_i$
by
$e_i$
by
![]() $e_{i+n}=\varpi e_i$
. Note that we have
$e_{i+n}=\varpi e_i$
. Note that we have
![]() $\tau e_i=e_{i+1}$
for any i. In the sequel, we identify
$\tau e_i=e_{i+1}$
for any i. In the sequel, we identify
![]() ${\mathcal {G}} r$
and
${\mathcal {G}} r$
and
![]() $\{M\subset L^n\ \text {lattice}\}$
by
$\{M\subset L^n\ \text {lattice}\}$
by
![]() $gK\mapsto g\mathcal O^n$
.
$gK\mapsto g\mathcal O^n$
.
Let
![]() $X_\mu (b)^0$
be a
$X_\mu (b)^0$
be a
![]() $\overline {\mathbb F}_q$
-subscheme of
$\overline {\mathbb F}_q$
-subscheme of
![]() $X_\mu (b)$
defined as
$X_\mu (b)$
defined as
![]() $X_\mu (b)^0=\{gK\in X_\mu (b)\mid \kappa (g)=0\}$
. We associate to
$X_\mu (b)^0=\{gK\in X_\mu (b)\mid \kappa (g)=0\}$
. We associate to
![]() $M\in X_\mu (b)^0$
an extended semi-module for
$M\in X_\mu (b)^0$
an extended semi-module for
![]() $\mu $
. Let
$\mu $
. Let
![]() $v\in L^n$
. Then we can write
$v\in L^n$
. Then we can write
![]() $v=\sum _{i\in \mathbb Z}[\alpha _i]e_i$
with
$v=\sum _{i\in \mathbb Z}[\alpha _i]e_i$
with
![]() $\alpha _i\in \overline {\mathbb F}_q$
and
$\alpha _i\in \overline {\mathbb F}_q$
and
![]() $\alpha _i=0$
for sufficiently small i. Here,
$\alpha _i=0$
for sufficiently small i. Here,
![]() $[\alpha _i]$
denotes the Teichmüller lift of
$[\alpha _i]$
denotes the Teichmüller lift of
![]() $\alpha _i$
if
$\alpha _i$
if
![]() $\operatorname {\mathrm {ch}} F=0$
and
$\operatorname {\mathrm {ch}} F=0$
and
![]() $[\alpha _i]=\alpha _i$
if
$[\alpha _i]=\alpha _i$
if
![]() $\operatorname {\mathrm {ch}} F>0$
. Let
$\operatorname {\mathrm {ch}} F>0$
. Let
For
![]() $M\in {\mathcal {G}} r$
, we define the set
$M\in {\mathcal {G}} r$
, we define the set
It is easy to check that if
![]() $M\in X_\mu (b)^0$
, then
$M\in X_\mu (b)^0$
, then
![]() $A(M)$
is a normalized semi-module for
$A(M)$
is a normalized semi-module for
![]() $m,n$
. We also define
$m,n$
. We also define
![]() $\varphi (M)\colon \mathbb Z\rightarrow \mathbb N\cup \{-\infty \}$
by
$\varphi (M)\colon \mathbb Z\rightarrow \mathbb N\cup \{-\infty \}$
by
 $$ \begin{align*}a\mapsto \begin{cases} \max\{k\mid \exists v\in M\setminus \{0\} \text{\ with\ }\mathcal I(v)=a, \varpi^{-k}b\sigma(v)\in M\} & (a\in A(M))\\ -\infty & (a\notin A(M)). \end{cases}\end{align*} $$
$$ \begin{align*}a\mapsto \begin{cases} \max\{k\mid \exists v\in M\setminus \{0\} \text{\ with\ }\mathcal I(v)=a, \varpi^{-k}b\sigma(v)\in M\} & (a\in A(M))\\ -\infty & (a\notin A(M)). \end{cases}\end{align*} $$
Lemma 3.5 Let
![]() $M\in X_\mu (b)^0$
. Then
$M\in X_\mu (b)^0$
. Then
![]() $(A(M), \varphi (M))$
is an extended semi-module for
$(A(M), \varphi (M))$
is an extended semi-module for
![]() $\mu $
.
$\mu $
.
Proof See [Reference Viehmann42, Lemma 4.1].
For an extended semi-module
![]() $(A,\varphi )$
for
$(A,\varphi )$
for
![]() $\mu $
, let
$\mu $
, let
Lemma 3.6 The set
![]() $S_{A,\varphi }$
is a locally closed subscheme of
$S_{A,\varphi }$
is a locally closed subscheme of
![]() $X_\mu (b)^0$
.
$X_\mu (b)^0$
.
Proof See [Reference Viehmann42, Lemma 4.2].
Let
![]() $\mathbb A_\mu $
be the set of extended semi-modules for
$\mathbb A_\mu $
be the set of extended semi-modules for
![]() $\mu $
. Set
$\mu $
. Set
![]() $\mathbb A_\mu ^{\mathrm {top}}= \{(A,\varphi )\in \mathbb A_\mu \mid \dim S_{A,\varphi }=\dim X_\mu (b)\}$
. By Proposition 3.7 below,
$\mathbb A_\mu ^{\mathrm {top}}= \{(A,\varphi )\in \mathbb A_\mu \mid \dim S_{A,\varphi }=\dim X_\mu (b)\}$
. By Proposition 3.7 below,
![]() $J_b(F)\backslash \operatorname {\mathrm {Irr}} X_\mu (b)$
is parametrized by
$J_b(F)\backslash \operatorname {\mathrm {Irr}} X_\mu (b)$
is parametrized by
![]() $\mathbb A_\mu ^{\mathrm {top}}$
. In the sequel, we also use the symbol
$\mathbb A_\mu ^{\mathrm {top}}$
. In the sequel, we also use the symbol
![]() $\mathbb A$
to denote the affine space as usual. We hope our notation will not cause confusions.
$\mathbb A$
to denote the affine space as usual. We hope our notation will not cause confusions.
For an extended semi-module
![]() $(A,\varphi )$
for
$(A,\varphi )$
for
![]() $\mu $
, let
$\mu $
, let
Proposition 3.7 Let
![]() $(A,\varphi )$
be an extended semi-module for
$(A,\varphi )$
be an extended semi-module for
![]() $\mu $
. There exists a nonempty open subscheme
$\mu $
. There exists a nonempty open subscheme
![]() $U_{A,\varphi }\subseteq \mathbb A^{|\mathcal V(A,\varphi )|}$
and a morphism
$U_{A,\varphi }\subseteq \mathbb A^{|\mathcal V(A,\varphi )|}$
and a morphism
![]() $U_{A,\varphi }\rightarrow S_{A,\varphi }$
which is bijective on
$U_{A,\varphi }\rightarrow S_{A,\varphi }$
which is bijective on
![]() $\overline {\mathbb F}_q$
-valued points. In particular,
$\overline {\mathbb F}_q$
-valued points. In particular,
![]() $S_{A,\varphi }$
is irreducible and of dimension
$S_{A,\varphi }$
is irreducible and of dimension
![]() $|\mathcal V(A,\varphi )|$
. Moreover, if
$|\mathcal V(A,\varphi )|$
. Moreover, if
![]() $(A,\varphi )$
is a cyclic extended semi-module, then
$(A,\varphi )$
is a cyclic extended semi-module, then
![]() $U_{A,\varphi }=\mathbb A^{|\mathcal V(A,\varphi )|}$
.
$U_{A,\varphi }=\mathbb A^{|\mathcal V(A,\varphi )|}$
.
Proof See [Reference Viehmann42, Theorem 4.3].
Here we briefly describe
![]() $U_{A,\varphi }$
and the map
$U_{A,\varphi }$
and the map
![]() $U_{A,\varphi }\rightarrow S_{A,\varphi }$
. For any
$U_{A,\varphi }\rightarrow S_{A,\varphi }$
. For any
![]() $x\in \overline {\mathbb F}_q^{|\mathcal V(A,\varphi )|}=\mathbb A^{|\mathcal V(A,\varphi )|}$
, we denote the coordinate of x by
$x\in \overline {\mathbb F}_q^{|\mathcal V(A,\varphi )|}=\mathbb A^{|\mathcal V(A,\varphi )|}$
, we denote the coordinate of x by
![]() $x_{a,c}$
. We associate to every x a set of elements
$x_{a,c}$
. We associate to every x a set of elements
![]() $\{v(a)\in L^n\mid a\in A\}$
which satisfies the following equations.
$\{v(a)\in L^n\mid a\in A\}$
which satisfies the following equations.
If
![]() $a=\max \bar A$
, then
$a=\max \bar A$
, then
For any other element
![]() $a\in \bar A$
, we want
$a\in \bar A$
, we want
where
![]() $v'=\varpi ^{-\varphi (a')}b\sigma (v(a'))$
for
$v'=\varpi ^{-\varphi (a')}b\sigma (v(a'))$
for
![]() $a'$
being minimal satisfying
$a'$
being minimal satisfying
![]() $a'+m-\varphi (a')n=a$
. For
$a'+m-\varphi (a')n=a$
. For
![]() $a\in n+A$
, we want
$a\in n+A$
, we want
Here
![]() $[x_{a,c}]$
denotes the Teichmüller lift of
$[x_{a,c}]$
denotes the Teichmüller lift of
![]() $x_{a,c}$
if
$x_{a,c}$
if
![]() $\operatorname {\mathrm {ch}} F=0$
and
$\operatorname {\mathrm {ch}} F=0$
and
![]() $[x_{a,c}]=x_{a,c}$
if
$[x_{a,c}]=x_{a,c}$
if
![]() $\operatorname {\mathrm {ch}} F>0$
. The set
$\operatorname {\mathrm {ch}} F>0$
. The set
![]() $\{v(a)\in L^n\mid a\in A\}$
is uniquely determined by the equations above. Hence, the map
$\{v(a)\in L^n\mid a\in A\}$
is uniquely determined by the equations above. Hence, the map
![]() $\mathbb A^{|\mathcal V(A,\varphi )|}\rightarrow {\mathcal {G}} r, x\mapsto \langle v(a)\rangle _{a\in A}$
is well-defined. By applying
$\mathbb A^{|\mathcal V(A,\varphi )|}\rightarrow {\mathcal {G}} r, x\mapsto \langle v(a)\rangle _{a\in A}$
is well-defined. By applying
![]() $\sigma $
on the above equations for x, we can easily check that this map is compatible with the action of
$\sigma $
on the above equations for x, we can easily check that this map is compatible with the action of
![]() $\sigma $
, i.e.,
$\sigma $
, i.e., ![]() maps to
maps to
![]() $\sigma \langle v(a)\rangle _{a\in A}$
. Let
$\sigma \langle v(a)\rangle _{a\in A}$
. Let
![]() $U_{A,\varphi }$
be the preimage of
$U_{A,\varphi }$
be the preimage of
![]() $S_{A,\varphi }$
under this map. Then
$S_{A,\varphi }$
under this map. Then
![]() $S_{A,\varphi }$
and hence
$S_{A,\varphi }$
and hence
![]() $U_{A,\varphi }$
are stable under
$U_{A,\varphi }$
are stable under
![]() $\sigma $
(because
$\sigma $
(because
![]() $\sigma (b)=b$
). In particular, we have
$\sigma (b)=b$
). In particular, we have
![]() $|S_{A,\varphi }^\sigma |=|U_{A,\varphi }^\sigma |$
. So if
$|S_{A,\varphi }^\sigma |=|U_{A,\varphi }^\sigma |$
. So if
![]() $(A,\varphi )$
is cyclic, then
$(A,\varphi )$
is cyclic, then
![]() $|S_{A,\varphi }^\sigma |=q^{|\mathcal V(A,\varphi )|}$
. Although not needed in this paper, it is also worth mentioning that if
$|S_{A,\varphi }^\sigma |=q^{|\mathcal V(A,\varphi )|}$
. Although not needed in this paper, it is also worth mentioning that if
![]() $(A,\varphi )$
is noncyclic, then
$(A,\varphi )$
is noncyclic, then
![]() $S_{A,\varphi }$
is never universally homeomorphic to an affine space.
$S_{A,\varphi }$
is never universally homeomorphic to an affine space.
Proposition 3.8 If
![]() $(A,\varphi )$
is noncyclic, then
$(A,\varphi )$
is noncyclic, then
![]() $|S_{A,\varphi }^\sigma |<q^{|\mathcal V(A,\varphi )|}$
. In particular,
$|S_{A,\varphi }^\sigma |<q^{|\mathcal V(A,\varphi )|}$
. In particular,
![]() $S_{A,\varphi }$
is never universally homeomorphic to an affine space.
$S_{A,\varphi }$
is never universally homeomorphic to an affine space.
Proof Let
![]() $x\in \mathbb A^{|\mathcal V(A,\varphi )|}$
. Note that if
$x\in \mathbb A^{|\mathcal V(A,\varphi )|}$
. Note that if
![]() $x_{a,c}=0$
for all
$x_{a,c}=0$
for all
![]() $(a,c)\in \mathcal V(A,\varphi )$
, then
$(a,c)\in \mathcal V(A,\varphi )$
, then
![]() $v(a)=e_a$
for all
$v(a)=e_a$
for all
![]() $a\in A$
. Set
$a\in A$
. Set
![]() $M=\langle e_a\rangle _{a\in A}$
. Then it is easy to check that
$M=\langle e_a\rangle _{a\in A}$
. Then it is easy to check that
![]() $(A(M),\varphi (M))$
is a cyclic semi-module for the dominant conjugate of the type of
$(A(M),\varphi (M))$
is a cyclic semi-module for the dominant conjugate of the type of
![]() $A(M)$
. So if
$A(M)$
. So if
![]() $(A,\varphi )$
is not cyclic, then
$(A,\varphi )$
is not cyclic, then
![]() $M\notin S_{A,\varphi }$
and hence
$M\notin S_{A,\varphi }$
and hence
![]() $|S_{A,\varphi }^\sigma |=|U_{A,\varphi }^\sigma |<q^{|\mathcal V(A,\varphi )|}$
. The last statement follows from [Reference Digne and Michel4, Propositions 4.1.12 and 8.1.11 (ii)].
$|S_{A,\varphi }^\sigma |=|U_{A,\varphi }^\sigma |<q^{|\mathcal V(A,\varphi )|}$
. The last statement follows from [Reference Digne and Michel4, Propositions 4.1.12 and 8.1.11 (ii)].
3.2 The stratification by extended semi-modules
For any
![]() $\lambda \in X_*(T)$
, set
$\lambda \in X_*(T)$
, set
![]() $A^\lambda =\{(i-1)+\lambda (i)n+k n \mid 1\le i\le n, k\in \mathbb N\}.$
It is easy to check that for a lattice
$A^\lambda =\{(i-1)+\lambda (i)n+k n \mid 1\le i\le n, k\in \mathbb N\}.$
It is easy to check that for a lattice
![]() $M\in I\varpi ^\lambda K/K$
, we have
$M\in I\varpi ^\lambda K/K$
, we have
![]() $A(M)=A^\lambda $
. Thus, we have the following lemma, which relates the semi-module stratification to the stratification by extended semi-modules.
$A(M)=A^\lambda $
. Thus, we have the following lemma, which relates the semi-module stratification to the stratification by extended semi-modules.
Lemma 3.9 Let
![]() $\lambda \in X_*(T)$
with
$\lambda \in X_*(T)$
with
![]() $\lambda (1)+\cdots +\lambda (n)=0$
. Then
$\lambda (1)+\cdots +\lambda (n)=0$
. Then
![]() $X_\mu ^{\lambda }(b)\neq \emptyset $
if and only if there exists an extended semi-module
$X_\mu ^{\lambda }(b)\neq \emptyset $
if and only if there exists an extended semi-module
![]() $(A^\lambda ,\varphi )$
for
$(A^\lambda ,\varphi )$
for
![]() $\mu $
. If this is the case, we have
$\mu $
. If this is the case, we have
where
![]() $\varphi $
runs over all the functions
$\varphi $
runs over all the functions
![]() $\mathbb Z\rightarrow \mathbb N\cup \{-\infty \}$
such that the pair of
$\mathbb Z\rightarrow \mathbb N\cup \{-\infty \}$
such that the pair of
![]() $A^\lambda $
and the function is an extended semi-module for
$A^\lambda $
and the function is an extended semi-module for
![]() $\mu $
.
$\mu $
.
For
![]() $\lambda \in X_*(T)$
with
$\lambda \in X_*(T)$
with
![]() $X_\mu ^\lambda (b)\neq \emptyset $
, let
$X_\mu ^\lambda (b)\neq \emptyset $
, let
![]() $1\le i_0\le n$
such that
$1\le i_0\le n$
such that
![]() $(i_0-1)+\lambda (i_0)n=\min \overline {A^\lambda }$
. Let
$(i_0-1)+\lambda (i_0)n=\min \overline {A^\lambda }$
. Let
![]() $1\le m_0<n$
be the residue of m modulo n, and let
$1\le m_0<n$
be the residue of m modulo n, and let
![]() $\lambda _{b,\operatorname {\mathrm {dom}}}$
be
$\lambda _{b,\operatorname {\mathrm {dom}}}$
be
![]() $((\lfloor \frac {m}{n} \rfloor +1)^{(m_0)},\lfloor \frac {m}{n} \rfloor ^{(n-m_0)})$
. Then
$((\lfloor \frac {m}{n} \rfloor +1)^{(m_0)},\lfloor \frac {m}{n} \rfloor ^{(n-m_0)})$
. Then
 $$ \begin{align*} &(i_0-1)+\lambda(i_0)n+m-(\lambda(i_0)+\lambda_{b,\operatorname{\mathrm{dom}}}(c^m(i_0))-\lambda(c^m(i_0)))n\\ {}&= c^m(i_0)-1+\lambda(c^m(i_0))n\in \overline {A^\lambda}, \end{align*} $$
$$ \begin{align*} &(i_0-1)+\lambda(i_0)n+m-(\lambda(i_0)+\lambda_{b,\operatorname{\mathrm{dom}}}(c^m(i_0))-\lambda(c^m(i_0)))n\\ {}&= c^m(i_0)-1+\lambda(c^m(i_0))n\in \overline {A^\lambda}, \end{align*} $$
where
![]() $c=s_1\cdots s_{n-1}$
. Repeating the same argument, we can check that the type of
$c=s_1\cdots s_{n-1}$
. Repeating the same argument, we can check that the type of
![]() $A^\lambda $
is a conjugate of
$A^\lambda $
is a conjugate of
![]() $b\lambda -\lambda =c^m\lambda +\lambda _{b,\operatorname {\mathrm {dom}}}-\lambda $
. By Lemma 3.4, an extended semi-module
$b\lambda -\lambda =c^m\lambda +\lambda _{b,\operatorname {\mathrm {dom}}}-\lambda $
. By Lemma 3.4, an extended semi-module
![]() $(A^\lambda ,\varphi )$
for
$(A^\lambda ,\varphi )$
for
![]() $\mu $
is cyclic if and only if
$\mu $
is cyclic if and only if
![]() $b\lambda -\lambda \in W_0\mu $
.
$b\lambda -\lambda \in W_0\mu $
.
Corollary 3.10 Let
![]() $\mu \in X_*(T)_+$
. If there exists a noncyclic semi-module for
$\mu \in X_*(T)_+$
. If there exists a noncyclic semi-module for
![]() $\mu $
, then the semi-module stratification of
$\mu $
, then the semi-module stratification of
![]() $X_{\preceq \mu }(b)$
is not a refinement of the -Oort stratification.
$X_{\preceq \mu }(b)$
is not a refinement of the -Oort stratification.
Proof Let
![]() $(A^\lambda ,\varphi )$
be a noncyclic semi-module for
$(A^\lambda ,\varphi )$
be a noncyclic semi-module for
![]() $\mu $
. Then we have
$\mu $
. Then we have
![]() $(b\lambda -\lambda )_{\operatorname {\mathrm {dom}}}\prec \mu $
by Lemma 3.4. On the other hand, there always exists a cyclic semi-module
$(b\lambda -\lambda )_{\operatorname {\mathrm {dom}}}\prec \mu $
by Lemma 3.4. On the other hand, there always exists a cyclic semi-module
![]() $(A^\lambda ,\varphi ')$
for
$(A^\lambda ,\varphi ')$
for
![]() $(b\lambda -\lambda )_{\operatorname {\mathrm {dom}}}$
. By Lemma 3.9,
$(b\lambda -\lambda )_{\operatorname {\mathrm {dom}}}$
. By Lemma 3.9,
![]() $X_{\preceq \mu }^\lambda (b)$
intersects both
$X_{\preceq \mu }^\lambda (b)$
intersects both
![]() $X_\mu (b)$
and
$X_\mu (b)$
and
![]() $X_{(b\lambda -\lambda )_{\operatorname {\mathrm {dom}}}}(b)$
. This implies that
$X_{(b\lambda -\lambda )_{\operatorname {\mathrm {dom}}}}(b)$
. This implies that
![]() $X_{\preceq \mu }^\lambda (b)$
is not contained in any set of the form
$X_{\preceq \mu }^\lambda (b)$
is not contained in any set of the form
![]() $\pi (X_w(b))$
with
$\pi (X_w(b))$
with
![]() $w\in \tilde W$
, which finishes the proof.
$w\in \tilde W$
, which finishes the proof.
For
![]() $\mu =(\mu (1),\ldots , \mu (n-1),0)\in X_*(T)_+$
, set
$\mu =(\mu (1),\ldots , \mu (n-1),0)\in X_*(T)_+$
, set
![]() $\mu ^*=(\mu (1), \mu (1)-\mu (n-1),\ldots ,\mu (1)-\mu (2),0)$
and
$\mu ^*=(\mu (1), \mu (1)-\mu (n-1),\ldots ,\mu (1)-\mu (2),0)$
and
![]() $b^*=\tau ^{n\mu (1)-m}$
. If
$b^*=\tau ^{n\mu (1)-m}$
. If
![]() $(A^\lambda ,\varphi )$
is an extended semi-module for
$(A^\lambda ,\varphi )$
is an extended semi-module for
![]() $\mu $
, then there exists
$\mu $
, then there exists
![]() $\varphi '\colon \mathbb Z\rightarrow \mathbb N\cup \{-\infty \}$
such that
$\varphi '\colon \mathbb Z\rightarrow \mathbb N\cup \{-\infty \}$
such that
![]() $(A^{-w_{\max }\lambda },\varphi ')$
is an extended semi-module for
$(A^{-w_{\max }\lambda },\varphi ')$
is an extended semi-module for
![]() $\mu ^*$
(see Section 2.4). Clearly,
$\mu ^*$
(see Section 2.4). Clearly,
![]() $b\lambda -\lambda \in W_0\mu $
if and only if
$b\lambda -\lambda \in W_0\mu $
if and only if
![]() $b^*(-w_{\max }\lambda )+w_{\max }\lambda \in -W_0\mu ^*$
. Thus, we have the following lemma.
$b^*(-w_{\max }\lambda )+w_{\max }\lambda \in -W_0\mu ^*$
. Thus, we have the following lemma.
Lemma 3.11 There exists a noncyclic extended semi-module for
![]() $\mu $
if and only if the same is true for
$\mu $
if and only if the same is true for
![]() $\mu ^*$
.
$\mu ^*$
.
3.3 The minuscule case
In this subsection, we treat the minuscule case. Consider
![]() $G^d$
with a Frobenius automorphism
$G^d$
with a Frobenius automorphism
![]() $\sigma _{\bullet }$
given by
$\sigma _{\bullet }$
given by
For
![]() $\mu _{\bullet }=(\mu _1, \ldots , \mu _d)\in X_*(T)^d_+$
and
$\mu _{\bullet }=(\mu _1, \ldots , \mu _d)\in X_*(T)^d_+$
and
![]() $b_{\bullet }=(1,\ldots , 1, b)\in G^d(L)$
with
$b_{\bullet }=(1,\ldots , 1, b)\in G^d(L)$
with
![]() $b\in G(L)$
, we define
$b\in G(L)$
, we define
![]() $X_{\mu _{\bullet }}(b_{\bullet })\subset {\mathcal {G}} r^d=G^d(L)/K^d$
as
$X_{\mu _{\bullet }}(b_{\bullet })\subset {\mathcal {G}} r^d=G^d(L)/K^d$
as
Let us denote by
![]() $\operatorname {\mathrm {Irr}} X_{\mu _{\bullet }}(b_{\bullet })$
the set of irreducible components of
$\operatorname {\mathrm {Irr}} X_{\mu _{\bullet }}(b_{\bullet })$
the set of irreducible components of
![]() $X_{\mu _{\bullet }}(b_{\bullet })$
. Through the identification
$X_{\mu _{\bullet }}(b_{\bullet })$
. Through the identification
![]() $J_b(F)\cong J_{b_{\bullet }}(F)$
given by
$J_b(F)\cong J_{b_{\bullet }}(F)$
given by
![]() $g\mapsto (g,\ldots ,g)$
, this set is equipped with an action of
$g\mapsto (g,\ldots ,g)$
, this set is equipped with an action of
![]() $J_b(F)$
.
$J_b(F)$
.
For minuscule
![]() $\mu _{\bullet }\in X_*(T)^d_+$
and
$\mu _{\bullet }\in X_*(T)^d_+$
and
![]() $b_{\bullet }=(1,\ldots ,1,b)\in G^d(L)$
, we define
$b_{\bullet }=(1,\ldots ,1,b)\in G^d(L)$
, we define
Here,
![]() $X_{\mu _{\bullet }}^{\lambda _{\bullet }}(b_{\bullet })$
denotes
$X_{\mu _{\bullet }}^{\lambda _{\bullet }}(b_{\bullet })$
denotes
![]() $X_{\mu _{\bullet }}(b_{\bullet })\cap I^d\varpi ^{\lambda _{\bullet }} K^d/K^d$
. For
$X_{\mu _{\bullet }}(b_{\bullet })\cap I^d\varpi ^{\lambda _{\bullet }} K^d/K^d$
. For
![]() $\lambda _{\bullet }, \lambda ^{\prime }_{\bullet }\in \mathcal A_{\mu _{\bullet }}^{\mathrm {top}}$
, we write
$\lambda _{\bullet }, \lambda ^{\prime }_{\bullet }\in \mathcal A_{\mu _{\bullet }}^{\mathrm {top}}$
, we write
![]() $\lambda _{\bullet }\sim \lambda ^{\prime }_{\bullet }$
if
$\lambda _{\bullet }\sim \lambda ^{\prime }_{\bullet }$
if
![]() $\lambda _{\bullet }=\tau ^k \lambda ^{\prime }_{\bullet }=(\tau ^k \lambda ^{\prime }_1,\ldots , \tau ^k \lambda ^{\prime }_d)$
for some
$\lambda _{\bullet }=\tau ^k \lambda ^{\prime }_{\bullet }=(\tau ^k \lambda ^{\prime }_1,\ldots , \tau ^k \lambda ^{\prime }_d)$
for some
![]() $k\in \mathbb Z$
. Let
$k\in \mathbb Z$
. Let
![]() $\mathbb A_{\mu _{\bullet }}^{\mathrm {top}}$
denote the set of equivalence classes with respect to
$\mathbb A_{\mu _{\bullet }}^{\mathrm {top}}$
denote the set of equivalence classes with respect to
![]() $\sim $
, and let
$\sim $
, and let
![]() $[\lambda _{\bullet }]\in \mathbb A_{\mu _{\bullet }}^{\mathrm {top}}$
denote the equivalence class represented by
$[\lambda _{\bullet }]\in \mathbb A_{\mu _{\bullet }}^{\mathrm {top}}$
denote the equivalence class represented by
![]() $\lambda _{\bullet }\in \mathcal A_{\mu _{\bullet }}^{\mathrm {top}}$
. Then
$\lambda _{\bullet }\in \mathcal A_{\mu _{\bullet }}^{\mathrm {top}}$
. Then
![]() $J_{b}(F)\backslash \operatorname {\mathrm {Irr}} X_{\mu _{\bullet }}(b_{\bullet })$
is parametrized by
$J_{b}(F)\backslash \operatorname {\mathrm {Irr}} X_{\mu _{\bullet }}(b_{\bullet })$
is parametrized by
![]() $\mathbb A_{\mu _{\bullet }}^{\mathrm {top}}$
as follows.
$\mathbb A_{\mu _{\bullet }}^{\mathrm {top}}$
as follows.
Proposition 3.12 Assume that
![]() $\mu _{\bullet }\in X_*(T)_+^d$
is minuscule. Then the map
$\mu _{\bullet }\in X_*(T)_+^d$
is minuscule. Then the map
![]() $\lambda _{\bullet }\mapsto \overline {X_{\mu _{\bullet }}^{\lambda _{\bullet }}(b_{\bullet })}$
induces a bijection
$\lambda _{\bullet }\mapsto \overline {X_{\mu _{\bullet }}^{\lambda _{\bullet }}(b_{\bullet })}$
induces a bijection
Proof See [Reference Hamacher and Viehmann18, Proposition 1.6]. Note that we have
![]() $\mathrm {Stab}_{J_b(F)} (X_{\mu _{\bullet }}^{\lambda _{\bullet }}(b_{\bullet }))=J_b(F)^0$
.
$\mathrm {Stab}_{J_b(F)} (X_{\mu _{\bullet }}^{\lambda _{\bullet }}(b_{\bullet }))=J_b(F)^0$
.
We also define
for
![]() $1\le j\le \dim X_{\mu _{\bullet }}(b_{\bullet })$
. We can similarly consider the equivalence relation
$1\le j\le \dim X_{\mu _{\bullet }}(b_{\bullet })$
. We can similarly consider the equivalence relation
![]() $\sim $
as above. If
$\sim $
as above. If
![]() $d=1$
, then
$d=1$
, then ![]() can be identified with (extended) semi-modules for
can be identified with (extended) semi-modules for
![]() $\mu $
whose corresponding stratum has dimension j, see Lemma 3.4 and Lemma 3.9.
$\mu $
whose corresponding stratum has dimension j, see Lemma 3.4 and Lemma 3.9.
Proposition 3.13 Set
![]() $\mu =\omega _i$
. Then we always have
$\mu =\omega _i$
. Then we always have
![]() $|\mathbb A_\mu ^{\mathrm {top}}|=|\mathbb A_\mu ^{0}|=1$
. If
$|\mathbb A_\mu ^{\mathrm {top}}|=|\mathbb A_\mu ^{0}|=1$
. If
![]() $i=2,n-2$
, then
$i=2,n-2$
, then
![]() $|\mathbb A_\mu ^j|=1$
for all
$|\mathbb A_\mu ^j|=1$
for all
![]() $0\le j\le \dim X_{\mu }(b)$
. If
$0\le j\le \dim X_{\mu }(b)$
. If
![]() $i=3,n-3$
, then
$i=3,n-3$
, then
![]() $|\mathbb A_\mu ^{\dim X_{\mu }(b)-1}|=2$
.
$|\mathbb A_\mu ^{\dim X_{\mu }(b)-1}|=2$
.
Proof We can easily check the equalities in the proposition using [Reference Hamacher and Viehmann18, Theorem 4.16] (cf. [Reference de Jong and Oort3, Remark 6.16]), which gives a combinatorial way of computing
![]() $|\mathbb A_\mu ^j|$
. In fact, all of the assertions except the last assertion follow from [Reference Viehmann43, Proposition 5.5].
$|\mathbb A_\mu ^j|$
. In fact, all of the assertions except the last assertion follow from [Reference Viehmann43, Proposition 5.5].
Example 3.14 We always have
![]() $\mathbb A_{\omega _i}^{0}=\{[0]\}$
.
$\mathbb A_{\omega _i}^{0}=\{[0]\}$
.
4 Crystal bases
Keep the notations and assumptions in Section 3.
4.1 Crystals and young tableaux
In this subsection, we first recall the definition of
![]() $\widehat G$
-crystals from [Reference Xiao and Zhu45, Definition 3.3.1].
$\widehat G$
-crystals from [Reference Xiao and Zhu45, Definition 3.3.1].
Definition 4.1 A (normal)
![]() $\widehat G$
-crystal is a finite set
$\widehat G$
-crystal is a finite set
![]() $\mathbb B$
, equipped with a weight map
$\mathbb B$
, equipped with a weight map
![]() $\operatorname {\mathrm {wt}}\colon \mathbb B\rightarrow X_*(T)$
, and operators
$\operatorname {\mathrm {wt}}\colon \mathbb B\rightarrow X_*(T)$
, and operators
![]() $\tilde e_\alpha , \tilde f_\alpha \colon \mathbb B\rightarrow \mathbb B\cup \{0\}$
for each
$\tilde e_\alpha , \tilde f_\alpha \colon \mathbb B\rightarrow \mathbb B\cup \{0\}$
for each
![]() $\alpha \in \Delta $
, such that
$\alpha \in \Delta $
, such that
-
(i) for every
 $\mathbf {b}\in \mathbb B$
, either
$\mathbf {b}\in \mathbb B$
, either
 $\tilde e_\alpha \mathbf {b}=0$
or
$\tilde e_\alpha \mathbf {b}=0$
or
 $\operatorname {\mathrm {wt}}(\tilde e_\alpha \mathbf {b})=\operatorname {\mathrm {wt}}(\mathbf {b})+\alpha ^\vee $
, and either
$\operatorname {\mathrm {wt}}(\tilde e_\alpha \mathbf {b})=\operatorname {\mathrm {wt}}(\mathbf {b})+\alpha ^\vee $
, and either
 $\tilde f_\alpha \mathbf {b}=0$
or
$\tilde f_\alpha \mathbf {b}=0$
or
 $\operatorname {\mathrm {wt}}(\tilde f_\alpha \mathbf {b})=\operatorname {\mathrm {wt}}(\mathbf {b})-\alpha ^\vee $
,
$\operatorname {\mathrm {wt}}(\tilde f_\alpha \mathbf {b})=\operatorname {\mathrm {wt}}(\mathbf {b})-\alpha ^\vee $
, -
(ii) for all
 $\mathbf {b}, \mathbf {b}'\in \mathbb B$
one has
$\mathbf {b}, \mathbf {b}'\in \mathbb B$
one has
 $\mathbf {b}'=\tilde e_\alpha \mathbf {b}$
if and only if
$\mathbf {b}'=\tilde e_\alpha \mathbf {b}$
if and only if
 $\mathbf {b}=\tilde f_\alpha \mathbf {b}'$
, and
$\mathbf {b}=\tilde f_\alpha \mathbf {b}'$
, and -
(iii) if
 $\varepsilon _\alpha , \phi _\alpha \colon \mathbb B\rightarrow \mathbb Z,\ \alpha \in \Delta $
are the maps defined by
$\varepsilon _\alpha , \phi _\alpha \colon \mathbb B\rightarrow \mathbb Z,\ \alpha \in \Delta $
are the maps defined by  $$ \begin{align*} \varepsilon_\alpha(\mathbf{b})=\max\{k\mid \tilde e_\alpha^k\mathbf{b}\neq 0\}\ \ \text{and}\ \ \phi_\alpha(\mathbf{b})=\max\{k\mid \tilde f_\alpha^k\mathbf{b}\neq 0\}, \end{align*} $$
$$ \begin{align*} \varepsilon_\alpha(\mathbf{b})=\max\{k\mid \tilde e_\alpha^k\mathbf{b}\neq 0\}\ \ \text{and}\ \ \phi_\alpha(\mathbf{b})=\max\{k\mid \tilde f_\alpha^k\mathbf{b}\neq 0\}, \end{align*} $$
then
 $\phi _\alpha (\mathbf {b})-\varepsilon _\alpha (\mathbf {b})=\langle \alpha , \operatorname {\mathrm {wt}}(\mathbf {b})\rangle $
.
$\phi _\alpha (\mathbf {b})-\varepsilon _\alpha (\mathbf {b})=\langle \alpha , \operatorname {\mathrm {wt}}(\mathbf {b})\rangle $
.
For a
![]() $\widehat G$
-crystal
$\widehat G$
-crystal
![]() $\mathbb B$
, let
$\mathbb B$
, let
![]() $\mathbb B^*=\{\mathbf {b}^*\mid \mathbf {b}\in \mathbb B\}$
be the dual
$\mathbb B^*=\{\mathbf {b}^*\mid \mathbf {b}\in \mathbb B\}$
be the dual
![]() $\widehat G$
-crystal. Setting
$\widehat G$
-crystal. Setting
![]() $0^*=0$
, the maps are given by
$0^*=0$
, the maps are given by
For
![]() $\lambda \in X_*(T)$
, we denote by
$\lambda \in X_*(T)$
, we denote by
![]() $\mathbb B(\lambda )$
the set of elements with weight
$\mathbb B(\lambda )$
the set of elements with weight
![]() $\lambda $
for
$\lambda $
for
![]() $\widehat G$
, called the weight space with weight
$\widehat G$
, called the weight space with weight
![]() $\lambda $
for
$\lambda $
for
![]() $\widehat G$
. Let
$\widehat G$
. Let
![]() $\mathbb B_1$
and
$\mathbb B_1$
and
![]() $\mathbb B_2$
be two
$\mathbb B_2$
be two
![]() $\widehat G$
-crystals. A morphism
$\widehat G$
-crystals. A morphism
![]() $\mathbb B_1\rightarrow \mathbb B_2$
is a map of underlying sets compatible with
$\mathbb B_1\rightarrow \mathbb B_2$
is a map of underlying sets compatible with
![]() $\operatorname {\mathrm {wt}},\tilde e_\alpha $
and
$\operatorname {\mathrm {wt}},\tilde e_\alpha $
and
![]() $\tilde f_\alpha $
.
$\tilde f_\alpha $
.
In the sequel, we write
![]() $\tilde e_i$
and
$\tilde e_i$
and
![]() $\tilde f_i$
(resp.
$\tilde f_i$
(resp.
![]() $\varepsilon _i$
and
$\varepsilon _i$
and
![]() $\phi _i$
) instead of
$\phi _i$
) instead of
![]() $\tilde e_{\chi _{i,i+1}}$
and
$\tilde e_{\chi _{i,i+1}}$
and
![]() $\tilde f_{\chi _{i,i+1}}$
(resp.
$\tilde f_{\chi _{i,i+1}}$
(resp.
![]() $\varepsilon _{\chi _{i,i+1}}$
and
$\varepsilon _{\chi _{i,i+1}}$
and
![]() $\phi _{\chi _{i,i+1}}$
) for simplicity.
$\phi _{\chi _{i,i+1}}$
) for simplicity.
Example 4.2 Let
![]() $\mathbb B_\mu $
be the crystal basis of the irreducible
$\mathbb B_\mu $
be the crystal basis of the irreducible
![]() $\widehat G$
-module of highest weight
$\widehat G$
-module of highest weight
![]() $\mu \in X_*(T)_+$
. Then
$\mu \in X_*(T)_+$
. Then
![]() $\mathbb B_\mu $
is a crystal. We call
$\mathbb B_\mu $
is a crystal. We call
![]() $\mathbb B_\mu $
a highest weight crystal of highest weight
$\mathbb B_\mu $
a highest weight crystal of highest weight
![]() $\mu $
(cf. [Reference Xiao and Zhu45, Definition 3.3.1(3)]). There exists a unique element
$\mu $
(cf. [Reference Xiao and Zhu45, Definition 3.3.1(3)]). There exists a unique element
![]() $\mathbf {b}_\mu \in \mathbb B_\mu $
satisfying
$\mathbf {b}_\mu \in \mathbb B_\mu $
satisfying
![]() $\tilde e_\alpha \mathbf {b}_\mu =0$
for all
$\tilde e_\alpha \mathbf {b}_\mu =0$
for all
![]() $\alpha $
,
$\alpha $
,
![]() $\operatorname {\mathrm {wt}}(\mathbf {b}_\mu )=\mu $
, and
$\operatorname {\mathrm {wt}}(\mathbf {b}_\mu )=\mu $
, and
![]() $\mathbb B_\mu $
is generated from
$\mathbb B_\mu $
is generated from
![]() $\mathbf {b}_\mu $
by the operators
$\mathbf {b}_\mu $
by the operators
![]() $\tilde f_\alpha $
.
$\tilde f_\alpha $
.
We give a realization of
![]() $\mathbb B_\mu $
by Young tableaux. This allows us to treat it in a combinatorial way.
$\mathbb B_\mu $
by Young tableaux. This allows us to treat it in a combinatorial way.
Definition 4.3 A Young diagram is a collection of boxes arranged in left-justified rows with a weakly decreasing number of boxes in each row. For a dominant cocharacter
![]() $\mu \in X_*(T)_+$
, we denote by
$\mu \in X_*(T)_+$
, we denote by
![]() $Y_\mu $
the Young diagram having
$Y_\mu $
the Young diagram having
![]() $\mu (i)$
boxes in the ith row. A skew Young diagram is a diagram obtained by removing a smaller Young diagram from a larger one that contains it. For dominant cocharacters
$\mu (i)$
boxes in the ith row. A skew Young diagram is a diagram obtained by removing a smaller Young diagram from a larger one that contains it. For dominant cocharacters
![]() $\mu ,\nu \in X_*(T)_+$
with
$\mu ,\nu \in X_*(T)_+$
with
![]() $\nu (i)\le \mu (i)$
, we denote by
$\nu (i)\le \mu (i)$
, we denote by
![]() $Y_{\mu /\nu }$
the skew Young diagram obtained by removing
$Y_{\mu /\nu }$
the skew Young diagram obtained by removing
![]() $Y_\nu $
from
$Y_\nu $
from
![]() $Y_\mu $
.
$Y_\mu $
.

Definition 4.4 A tableau is a (skew) Young diagram filled with numbers, one for each box. A semi-standard tableau is a tableau obtained from a (skew) Young diagram by filling the boxes with the numbers
![]() $1,2,\ldots , n$
subject to the conditions
$1,2,\ldots , n$
subject to the conditions
-
(i) the entries in each row are weakly increasing from left to right,
-
(ii) the entries in each column are strictly increasing from top to bottom.

Let
![]() $K_{\mu /\nu }(\lambda )$
be the number of all semi-standard tableaux
$K_{\mu /\nu }(\lambda )$
be the number of all semi-standard tableaux
![]() $\mathbf {b}$
of shape
$\mathbf {b}$
of shape
![]() $Y_{\mu /\nu }$
such that the number of
$Y_{\mu /\nu }$
such that the number of ![]() appearing in
appearing in
![]() $\mathbf {b}$
is
$\mathbf {b}$
is
![]() $\lambda (i)$
for
$\lambda (i)$
for
![]() $1\le i\le n$
. This is sometimes called the Kostka number. In Section 4.3, we need the following well-known result.
$1\le i\le n$
. This is sometimes called the Kostka number. In Section 4.3, we need the following well-known result.
Proposition 4.5 Let
![]() $\lambda ,\lambda '\in X_*(T)_+$
. If
$\lambda ,\lambda '\in X_*(T)_+$
. If
![]() $\lambda \preceq \lambda '$
, then
$\lambda \preceq \lambda '$
, then
![]() $K_{\mu /\nu }(\lambda ')\le K_{\mu /\nu }(\lambda )$
. In particular,
$K_{\mu /\nu }(\lambda ')\le K_{\mu /\nu }(\lambda )$
. In particular,
![]() $K_{\mu /\nu }(\lambda ')\neq 0$
implies
$K_{\mu /\nu }(\lambda ')\neq 0$
implies
![]() $K_{\mu /\nu }(\lambda )\neq 0$
.
$K_{\mu /\nu }(\lambda )\neq 0$
.
Proof See [Reference Fayers5, Proposition 1.2] and the remark right after the proposition.
We denote by
![]() $\mathcal B(Y)$
the set of all semi-standard tableaux of shape Y.
$\mathcal B(Y)$
the set of all semi-standard tableaux of shape Y.
Theorem 4.6 Let
![]() $\mu =(\mu (1),\ldots ,\mu (n))\in X_*(T)_+\setminus \{0\}$
with
$\mu =(\mu (1),\ldots ,\mu (n))\in X_*(T)_+\setminus \{0\}$
with
![]() $\mu (n)=0$
. Then
$\mu (n)=0$
. Then
![]() $\mathcal B(Y_\mu )$
has a crystal structure. Moreover, the crystal
$\mathcal B(Y_\mu )$
has a crystal structure. Moreover, the crystal
![]() $\mathcal B(Y_\mu )$
is isomorphic to
$\mathcal B(Y_\mu )$
is isomorphic to
![]() $\mathbb B_\mu $
.
$\mathbb B_\mu $
.
Proof This is [Reference Hong and Kang25, Theorems 7.3.6 and 7.4.1].
In the sequel, we identify
![]() $\mathbb B_\mu $
and
$\mathbb B_\mu $
and
![]() $\mathcal B(Y)$
by Theorem 4.6. For a semi-standard tableau
$\mathcal B(Y)$
by Theorem 4.6. For a semi-standard tableau
![]() $\mathbf {b}\in \mathbb B_\mu $
, let
$\mathbf {b}\in \mathbb B_\mu $
, let
![]() $k_i$
denote the number of i’s appearing in
$k_i$
denote the number of i’s appearing in
![]() $\mathbf {b}$
. Then the weight map
$\mathbf {b}$
. Then the weight map
![]() $\operatorname {\mathrm {wt}}$
on
$\operatorname {\mathrm {wt}}$
on
![]() $\mathbb B_\mu $
is given by
$\mathbb B_\mu $
is given by
![]() $\operatorname {\mathrm {wt}}(\mathbf {b})=(k_1,\ldots , k_n)$
. The following result is an explicit description of the actions of
$\operatorname {\mathrm {wt}}(\mathbf {b})=(k_1,\ldots , k_n)$
. The following result is an explicit description of the actions of
![]() $\tilde e_i$
and
$\tilde e_i$
and
![]() $\tilde f_i$
on
$\tilde f_i$
on
![]() $\mathbb B_\mu $
.
$\mathbb B_\mu $
.
Theorem 4.7 The actions of
![]() $\tilde e_i$
and
$\tilde e_i$
and
![]() $\tilde f_i$
on
$\tilde f_i$
on
![]() $\mathbf {b}\in \mathbb B_\mu $
can be computed by following the steps below:
$\mathbf {b}\in \mathbb B_\mu $
can be computed by following the steps below:
-
(i) In the Far-Eastern reading
 $\mathbf {b}_1\otimes \cdots \otimes \mathbf {b}_N$
of
$\mathbf {b}_1\otimes \cdots \otimes \mathbf {b}_N$
of
 $\mathbf {b}$
, we identify i (resp.
$\mathbf {b}$
, we identify i (resp.
 $\fbox{$i$+1}$
) by
$\fbox{$i$+1}$
) by
 $+$
(resp.
$+$
(resp.
 $-$
) and neglect other boxes.
$-$
) and neglect other boxes. -
(ii) Let
 $u_i(\mathbf {b})=u^1u^2\cdots u^l\ (u^j\in \{\pm \})$
be the sequence obtained by (i). If there is “
$u_i(\mathbf {b})=u^1u^2\cdots u^l\ (u^j\in \{\pm \})$
be the sequence obtained by (i). If there is “
 $+-$
” in
$+-$
” in
 $u(\mathbf {b})$
, then we neglect such a pair. We continue this procedure as far as we can.
$u(\mathbf {b})$
, then we neglect such a pair. We continue this procedure as far as we can. -
(iii) Let
 $u_i(\mathbf {b})_{\operatorname {\mathrm {red}}}=-\cdots -+\cdots +$
be the sequence obtained by (ii). Then
$u_i(\mathbf {b})_{\operatorname {\mathrm {red}}}=-\cdots -+\cdots +$
be the sequence obtained by (ii). Then
 $\tilde e_i$
changes the rightmost
$\tilde e_i$
changes the rightmost
 $-$
in
$-$
in
 $u_i(\mathbf {b})_{\operatorname {\mathrm {red}}}$
to
$u_i(\mathbf {b})_{\operatorname {\mathrm {red}}}$
to
 $+$
, and
$+$
, and
 $\tilde f_i$
changes the leftmost
$\tilde f_i$
changes the leftmost
 $+$
in
$+$
in
 $u_i(\mathbf {b})_{\operatorname {\mathrm {red}}}$
to
$u_i(\mathbf {b})_{\operatorname {\mathrm {red}}}$
to
 $-$
. If there is no such
$-$
. If there is no such
 $-$
(resp.
$-$
(resp.
 $+$
), then
$+$
), then
 $\tilde e_i\mathbf {b}=0$
(resp.
$\tilde e_i\mathbf {b}=0$
(resp.
 $\tilde f_i \mathbf {b}=0$
).
$\tilde f_i \mathbf {b}=0$
).
Moreover,
![]() $\varepsilon _i(\mathbf {b})$
(resp.
$\varepsilon _i(\mathbf {b})$
(resp.
![]() $\phi _i(\mathbf {b})$
) is equal to the number of
$\phi _i(\mathbf {b})$
) is equal to the number of
![]() $-$
(resp.
$-$
(resp.
![]() $+$
) in
$+$
) in
![]() $u_i(\mathbf {b})_{\operatorname {\mathrm {red}}}$
.
$u_i(\mathbf {b})_{\operatorname {\mathrm {red}}}$
.
Proof The first statement is [Reference Kashiwara and Nakashima27, Theorem 3.4.2]. The second statement follows immediately from this.
Next we recall the Weyl group action on crystals. Let
![]() $\mathbb B$
be a
$\mathbb B$
be a
![]() $\widehat G$
-crystal. For any
$\widehat G$
-crystal. For any
![]() $1\le i\le n-1$
and
$1\le i\le n-1$
and
![]() $\mathbf {b}\in \mathbb B$
, we set
$\mathbf {b}\in \mathbb B$
, we set
 $$ \begin{align*} s_i\mathbf{b}= \begin{cases} \tilde f_i^{\langle \chi_{i, i+1}, \operatorname{\mathrm{wt}}(\mathbf{b})\rangle}\mathbf{b} & \text{if } \langle \chi_{i, i+1}, \operatorname{\mathrm{wt}}(\mathbf{b})\rangle \geq 0\\ \tilde e_i^{-\langle \chi_{i, i+1}, \operatorname{\mathrm{wt}}(\mathbf{b})\rangle}\mathbf{b} & \text{if } \langle \chi_{i, i+1}, \operatorname{\mathrm{wt}}(\mathbf{b})\rangle \le 0. \end{cases} \end{align*} $$
$$ \begin{align*} s_i\mathbf{b}= \begin{cases} \tilde f_i^{\langle \chi_{i, i+1}, \operatorname{\mathrm{wt}}(\mathbf{b})\rangle}\mathbf{b} & \text{if } \langle \chi_{i, i+1}, \operatorname{\mathrm{wt}}(\mathbf{b})\rangle \geq 0\\ \tilde e_i^{-\langle \chi_{i, i+1}, \operatorname{\mathrm{wt}}(\mathbf{b})\rangle}\mathbf{b} & \text{if } \langle \chi_{i, i+1}, \operatorname{\mathrm{wt}}(\mathbf{b})\rangle \le 0. \end{cases} \end{align*} $$
Then we have the obvious relation
By [Reference Kashiwara26, Theorem 7.2.2], this extends to the action of the Weyl group
![]() $W_0$
on
$W_0$
on
![]() $\mathbb B$
, which is compatible with the action on
$\mathbb B$
, which is compatible with the action on
![]() $X_*(T)$
. For example,
$X_*(T)$
. For example,
![]() $w_{\max }\mathbf {b}_{\mu }\in \mathbb B_\mu $
has the lowest weight
$w_{\max }\mathbf {b}_{\mu }\in \mathbb B_\mu $
has the lowest weight
![]() $w_{\max }\mu $
. It is well-known that the dual of
$w_{\max }\mu $
. It is well-known that the dual of
![]() $\mathbb B_\mu $
is isomorphic to
$\mathbb B_\mu $
is isomorphic to
![]() $\mathbb B_{-w_{\max }\mu }$
(see for example [Reference Hong and Kang25, Lemma 3.5.2]).
$\mathbb B_{-w_{\max }\mu }$
(see for example [Reference Hong and Kang25, Lemma 3.5.2]).
Lemma 4.8 Let
![]() $w, w'\in W_0$
and
$w, w'\in W_0$
and
![]() $\mathbf {b}\in \mathbb B$
. If
$\mathbf {b}\in \mathbb B$
. If
![]() $w(\operatorname {\mathrm {wt}}(\mathbf {b}))=w'(\operatorname {\mathrm {wt}}(\mathbf {b}))$
, then
$w(\operatorname {\mathrm {wt}}(\mathbf {b}))=w'(\operatorname {\mathrm {wt}}(\mathbf {b}))$
, then
![]() $w\mathbf {b}=w'\mathbf {b}$
.
$w\mathbf {b}=w'\mathbf {b}$
.
Proof This is [Reference Shimada40, Lemma 3.10].
Let
![]() $\mathbf {b}\in \mathbb B(\lambda )$
. If
$\mathbf {b}\in \mathbb B(\lambda )$
. If
![]() $\lambda '$
is a conjugate of
$\lambda '$
is a conjugate of
![]() $\lambda $
, i.e., there exists
$\lambda $
, i.e., there exists
![]() $w\in W_0$
such that
$w\in W_0$
such that
![]() $\lambda '=w\lambda $
, then we call
$\lambda '=w\lambda $
, then we call
![]() $w\mathbf {b}$
the conjugate of
$w\mathbf {b}$
the conjugate of
![]() $\mathbf {b}$
with weight
$\mathbf {b}$
with weight
![]() $\lambda '$
. By Lemma 4.8, this does not depend on the choice of w.
$\lambda '$
. By Lemma 4.8, this does not depend on the choice of w.
Finally we consider the minuscule case. If
![]() $\mu \in X_*(T)_+$
is minuscule, then
$\mu \in X_*(T)_+$
is minuscule, then
![]() $\operatorname {\mathrm {wt}}\colon \mathbb B_\mu \rightarrow X_*(T)$
gives an identification between
$\operatorname {\mathrm {wt}}\colon \mathbb B_\mu \rightarrow X_*(T)$
gives an identification between
![]() $\mathbb B_\mu $
and the set of cocharacters which are conjugate to
$\mathbb B_\mu $
and the set of cocharacters which are conjugate to
![]() $\mu $
. Suppose
$\mu $
. Suppose
![]() $\mu _{\bullet }=(\mu _1,\ldots ,\mu _d)\in X_*(T)_+^d$
is minuscule. We can also identify
$\mu _{\bullet }=(\mu _1,\ldots ,\mu _d)\in X_*(T)_+^d$
is minuscule. We can also identify ![]() with the set of cocharacters in
with the set of cocharacters in
![]() $X_*(T)^d$
which are conjugate to
$X_*(T)^d$
which are conjugate to
![]() $\mu _{\bullet }$
.
$\mu _{\bullet }$
.
For
![]() $1\le k<n$
, let
$1\le k<n$
, let
![]() $\omega _k$
be the cocharacter of the form
$\omega _k$
be the cocharacter of the form
![]() $(1,\ldots ,1,0,\ldots ,0)$
in which
$(1,\ldots ,1,0,\ldots ,0)$
in which
![]() $1$
is repeated k times. Assume that each
$1$
is repeated k times. Assume that each
![]() $\mu _i$
is equal to
$\mu _i$
is equal to
![]() $\omega _{k_i}$
for some
$\omega _{k_i}$
for some
![]() $1\le k_i<n$
and
$1\le k_i<n$
and
![]() $i\le j$
if and only if
$i\le j$
if and only if
![]() $k_i\le k_j$
. In the rest of paper, we call such
$k_i\le k_j$
. In the rest of paper, we call such
![]() $\mu _{\bullet }$
Far-Eastern. If
$\mu _{\bullet }$
Far-Eastern. If
![]() $\mu _{\bullet }$
is Far-Eastern, then
$\mu _{\bullet }$
is Far-Eastern, then ![]() is dominant and its last entry is
is dominant and its last entry is
![]() $0$
. Let
$0$
. Let
![]() $\operatorname {\mathrm {FE}}\colon \mathbb B_{|\mu _{\bullet }|}\rightarrow \mathbb B_{\mu _{\bullet }}^{\widehat G^d}$
be a map defined by decomposing
$\operatorname {\mathrm {FE}}\colon \mathbb B_{|\mu _{\bullet }|}\rightarrow \mathbb B_{\mu _{\bullet }}^{\widehat G^d}$
be a map defined by decomposing
![]() $\mathbf {b}\in \mathbb B_\mu $
into its columns from right to left. We call
$\mathbf {b}\in \mathbb B_\mu $
into its columns from right to left. We call
![]() $\operatorname {\mathrm {FE}}$
the Far-Eastern reading.
$\operatorname {\mathrm {FE}}$
the Far-Eastern reading.
4.2 Construction of extended semi-modules
In this subsection, we recall from [Reference Shimada40, Section 4.2] the way of constructing extended semi-modules. See [Reference Shimada40, Section 4.3] for some examples of computation. Let
![]() $\mu _{\bullet }\in X_*(T)^d_+$
be a Far-Eastern cocharacter. Set
$\mu _{\bullet }\in X_*(T)^d_+$
be a Far-Eastern cocharacter. Set
![]() $\mu =|\mu _{\bullet }|$
.
$\mu =|\mu _{\bullet }|$
.
Let
![]() $\lambda _b$
denote the cocharacter whose i-th entry is
$\lambda _b$
denote the cocharacter whose i-th entry is
![]() $\lfloor \frac {im}{n}\rfloor -\lfloor \frac {(i-1)m}{n}\rfloor $
. Set
$\lfloor \frac {im}{n}\rfloor -\lfloor \frac {(i-1)m}{n}\rfloor $
. Set
![]() $\lambda _b^{\operatorname {\mathrm {op}}}=w_{\max }\lambda _b$
. For any
$\lambda _b^{\operatorname {\mathrm {op}}}=w_{\max }\lambda _b$
. For any
![]() $\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
, we denote by
$\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
, we denote by
![]() $\mathbf {b}^{\operatorname {\mathrm {op}}}$
the conjugate of
$\mathbf {b}^{\operatorname {\mathrm {op}}}$
the conjugate of
![]() $\mathbf {b}$
with weight
$\mathbf {b}$
with weight
![]() $\lambda _b^{\operatorname {\mathrm {op}}}$
. Let
$\lambda _b^{\operatorname {\mathrm {op}}}$
. Let
![]() $1\le m_0<n$
be the residue of m modulo n. Note that each entry of
$1\le m_0<n$
be the residue of m modulo n. Note that each entry of
![]() $\lambda _b$
is
$\lambda _b$
is
![]() $\lfloor \frac {m}{n} \rfloor $
or
$\lfloor \frac {m}{n} \rfloor $
or
![]() $\lfloor \frac {m}{n} \rfloor +1$
and
$\lfloor \frac {m}{n} \rfloor +1$
and
![]() $\lambda _b(i)=\lambda _b(n+1-i)$
for any
$\lambda _b(i)=\lambda _b(n+1-i)$
for any
![]() $2\le i\le n-1$
. Let
$2\le i\le n-1$
. Let
![]() $i_0=1<i_1<i_2<\cdots <i_{m_0}=n$
be the integers such that
$i_0=1<i_1<i_2<\cdots <i_{m_0}=n$
be the integers such that
![]() $\lambda _b(i_1)=\lambda _b(i_2)=\cdots =\lambda _b(i_{m_0})=\lfloor \frac {m}{n} \rfloor +1$
. Then
$\lambda _b(i_1)=\lambda _b(i_2)=\cdots =\lambda _b(i_{m_0})=\lfloor \frac {m}{n} \rfloor +1$
. Then
Here
![]() $\lambda _b(i)=\lfloor \frac {m}{n} \rfloor $
(resp.
$\lambda _b(i)=\lfloor \frac {m}{n} \rfloor $
(resp.
![]() $\lambda _b(i+1)=\lfloor \frac {m}{n} \rfloor $
) if and only if
$\lambda _b(i+1)=\lfloor \frac {m}{n} \rfloor $
) if and only if
![]() $s_{i-1}s_i\le w_{\max }'$
(resp.
$s_{i-1}s_i\le w_{\max }'$
(resp.
![]() $s_is_{i+1}\le w_{\max }'$
). By Lemma 4.8, it follows that
$s_is_{i+1}\le w_{\max }'$
). By Lemma 4.8, it follows that
![]() $\mathbf {b}^{\operatorname {\mathrm {op}}}$
can be computed by the action of the Coxeter element
$\mathbf {b}^{\operatorname {\mathrm {op}}}$
can be computed by the action of the Coxeter element
![]() $w_{\max }'$
. In this computation, each
$w_{\max }'$
. In this computation, each
![]() $s_i$
acts as the action of
$s_i$
acts as the action of
![]() $\tilde e_i$
because
$\tilde e_i$
because
![]() $\lfloor \frac {m}{n} \rfloor -(\lfloor \frac {m}{n} \rfloor +1)=-1$
. Therefore, if we write
$\lfloor \frac {m}{n} \rfloor -(\lfloor \frac {m}{n} \rfloor +1)=-1$
. Therefore, if we write
then there exists
![]() $(w_1, \ldots , w_{d})\in W_0^d$
such that
$(w_1, \ldots , w_{d})\in W_0^d$
such that
and each simple reflection appears exactly once in some
![]() $\operatorname {\mathrm {supp}}(w_j)$
.
$\operatorname {\mathrm {supp}}(w_j)$
.
Lemma 4.9 The tuple
![]() $(w_1,\ldots ,w_d)\in W_0^d$
as above is uniquely determined by
$(w_1,\ldots ,w_d)\in W_0^d$
as above is uniquely determined by
![]() $\mathbf {b}$
. In particular,
$\mathbf {b}$
. In particular, ![]() is a Coxeter element uniquely determined by
is a Coxeter element uniquely determined by
![]() $\mathbf {b}$
.
$\mathbf {b}$
.
Proof This is [Reference Shimada40, Lemma 4.3].
Set
![]() $w(\mathbf {b})=w_1^{-1}\cdots w_d^{-1}$
and
$w(\mathbf {b})=w_1^{-1}\cdots w_d^{-1}$
and
![]() $\Upsilon (\mathbf {b})=\{\upsilon \in W_0\mid \upsilon ^{-1}c^m \upsilon =w(\mathbf {b})\}$
, where
$\Upsilon (\mathbf {b})=\{\upsilon \in W_0\mid \upsilon ^{-1}c^m \upsilon =w(\mathbf {b})\}$
, where
![]() $c=s_1s_2\cdots s_{n-1}$
. Clearly
$c=s_1s_2\cdots s_{n-1}$
. Clearly
![]() $|\Upsilon (\mathbf {b})|=n$
.
$|\Upsilon (\mathbf {b})|=n$
.
For any
![]() $\mathbf {b}'\in \mathbb B_{\mu }$
, set
$\mathbf {b}'\in \mathbb B_{\mu }$
, set
Let
![]() $\lambda _b^-$
be the anti-dominant conjugate of
$\lambda _b^-$
be the anti-dominant conjugate of
![]() $\lambda _b$
, and let
$\lambda _b$
, and let
![]() $\mathbf {b}^-$
be the conjugate of
$\mathbf {b}^-$
be the conjugate of
![]() $\mathbf {b}$
with weight
$\mathbf {b}$
with weight
![]() $\lambda _b^-$
. For any
$\lambda _b^-$
. For any
![]() $\mathbf {b}\in \mathbb B_{\mu }(\lambda _b)$
and
$\mathbf {b}\in \mathbb B_{\mu }(\lambda _b)$
and
![]() $\upsilon \in \Upsilon (\mathbf {b})$
, we define
$\upsilon \in \Upsilon (\mathbf {b})$
, we define
![]() $\xi _{{\bullet }}(\mathbf {b}, \upsilon )\in X_*(T)^d$
by
$\xi _{{\bullet }}(\mathbf {b}, \upsilon )\in X_*(T)^d$
by
Let
![]() $C\in \operatorname {\mathrm {Irr}} X_\mu (b)^0$
. By Proposition 3.7,
$C\in \operatorname {\mathrm {Irr}} X_\mu (b)^0$
. By Proposition 3.7,
![]() $C=\overline {S_{A,\varphi }}$
for some
$C=\overline {S_{A,\varphi }}$
for some
![]() $(A,\varphi )\in \mathbb A^{\mathrm {top}}_\mu $
. On the other hand, by Proposition 3.12 and [Reference Nie32, Proposition 3.13], there exists a unique
$(A,\varphi )\in \mathbb A^{\mathrm {top}}_\mu $
. On the other hand, by Proposition 3.12 and [Reference Nie32, Proposition 3.13], there exists a unique
![]() $\lambda _{\bullet }\in \mathcal A_{\mu _{\bullet }}^{\mathrm {top}}$
with
$\lambda _{\bullet }\in \mathcal A_{\mu _{\bullet }}^{\mathrm {top}}$
with
![]() $\lambda _1(1)+\cdots +\lambda _1(n)=0$
such that
$\lambda _1(1)+\cdots +\lambda _1(n)=0$
such that
![]() $C=\operatorname {\mathrm {pr}}(\overline {X_{\mu _{\bullet }}^{\lambda _{\bullet }}(b_{\bullet })})$
. Here
$C=\operatorname {\mathrm {pr}}(\overline {X_{\mu _{\bullet }}^{\lambda _{\bullet }}(b_{\bullet })})$
. Here
![]() $\operatorname {\mathrm {pr}}\ \colon\ {\mathcal {G}} r^d\rightarrow {\mathcal {G}} r$
denotes the projection to the first factor. The following theorem is established in [Reference Shimada40, Theorem 4.4] by the author.
$\operatorname {\mathrm {pr}}\ \colon\ {\mathcal {G}} r^d\rightarrow {\mathcal {G}} r$
denotes the projection to the first factor. The following theorem is established in [Reference Shimada40, Theorem 4.4] by the author.
Theorem 4.10 We have
![]() $\upsilon _{\xi _j(\mathbf {b},\upsilon )}=\upsilon w_1^{-1}\cdots w_{j-1}^{-1}$
and
$\upsilon _{\xi _j(\mathbf {b},\upsilon )}=\upsilon w_1^{-1}\cdots w_{j-1}^{-1}$
and
![]() $\xi _{{\bullet }}(\mathbf {b},\upsilon )\in \mathcal A_{\mu _{\bullet }}^{\mathrm {top}}$
. If
$\xi _{{\bullet }}(\mathbf {b},\upsilon )\in \mathcal A_{\mu _{\bullet }}^{\mathrm {top}}$
. If
![]() $\upsilon '$
is an element in
$\upsilon '$
is an element in
![]() $\Upsilon (\mathbf {b})$
different from
$\Upsilon (\mathbf {b})$
different from
![]() $\upsilon '$
, then
$\upsilon '$
, then
![]() $\xi _{{\bullet }}(\mathbf {b}, \upsilon )\sim \xi _{{\bullet }}(\mathbf {b}, \upsilon ')$
. Let
$\xi _{{\bullet }}(\mathbf {b}, \upsilon )\sim \xi _{{\bullet }}(\mathbf {b}, \upsilon ')$
. Let
![]() $\xi _{\bullet }^0(\mathbf {b})$
be the unique cocharacter in
$\xi _{\bullet }^0(\mathbf {b})$
be the unique cocharacter in
![]() $[\xi _{\bullet }(\mathbf {b}, \upsilon )]$
such that
$[\xi _{\bullet }(\mathbf {b}, \upsilon )]$
such that
![]() $\xi _1^0(\mathbf {b})(1)+\cdots +\xi _1^0(\mathbf {b})(n)=0$
. Then for any
$\xi _1^0(\mathbf {b})(1)+\cdots +\xi _1^0(\mathbf {b})(n)=0$
. Then for any
![]() $(A,\varphi )\in \mathbb A^{\mathrm {top}}_\mu $
, there exists a unique
$(A,\varphi )\in \mathbb A^{\mathrm {top}}_\mu $
, there exists a unique
![]() $\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
such that
$\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
such that
![]() $\overline {S_{A,\varphi }}=\operatorname {\mathrm {pr}}(\overline {X_{\mu _{\bullet }}^{\xi _{\bullet }^0(\mathbf {b})}(b_{\bullet })})$
.
$\overline {S_{A,\varphi }}=\operatorname {\mathrm {pr}}(\overline {X_{\mu _{\bullet }}^{\xi _{\bullet }^0(\mathbf {b})}(b_{\bullet })})$
.
Proof This is [Reference Shimada40, Theorem 4.4].
This correspondence between
![]() $\mathbb A^{\mathrm {top}}_\mu $
and
$\mathbb A^{\mathrm {top}}_\mu $
and
![]() $\mathbb B_\mu (\lambda _b)$
is compatible with the natural bijection in the Chen-Zhu conjecture constructed by Nie in [Reference Nie32].
$\mathbb B_\mu (\lambda _b)$
is compatible with the natural bijection in the Chen-Zhu conjecture constructed by Nie in [Reference Nie32].
Corollary 4.11 Let
![]() $(A,\varphi )\in \mathbb A^{\mathrm {top}}_\mu $
. Let
$(A,\varphi )\in \mathbb A^{\mathrm {top}}_\mu $
. Let
![]() $\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
such that
$\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
such that
![]() $\overline {S_{A,\varphi }}=\operatorname {\mathrm {pr}}(\overline {X_{\mu _{\bullet }}^{\xi _{\bullet }^0(\mathbf {b})}(b_{\bullet })})$
. Then
$\overline {S_{A,\varphi }}=\operatorname {\mathrm {pr}}(\overline {X_{\mu _{\bullet }}^{\xi _{\bullet }^0(\mathbf {b})}(b_{\bullet })})$
. Then
![]() $(A,\varphi )$
is cyclic if and only if
$(A,\varphi )$
is cyclic if and only if
Proof By Lemma 3.9, we have
![]() $A=A^{\xi _1^0(\mathbf {b})}$
. Recall that
$A=A^{\xi _1^0(\mathbf {b})}$
. Recall that
![]() $(A,\varphi )$
is cyclic if and only if
$(A,\varphi )$
is cyclic if and only if
![]() $b\xi _1^0(\mathbf {b})-\xi _1^0(\mathbf {b})\in W_0\mu $
. Since
$b\xi _1^0(\mathbf {b})-\xi _1^0(\mathbf {b})\in W_0\mu $
. Since
![]() $b\xi _1^0(\mathbf {b})-\xi _1^0(\mathbf {b})$
is a conjugate of
$b\xi _1^0(\mathbf {b})-\xi _1^0(\mathbf {b})$
is a conjugate of
![]() $b\xi _1(\mathbf {b},\upsilon )-\xi _1(\mathbf {b},\upsilon )$
, this is also equivalent to
$b\xi _1(\mathbf {b},\upsilon )-\xi _1(\mathbf {b},\upsilon )$
, this is also equivalent to
![]() $\upsilon ^{-1}b\xi _1(\mathbf {b},\upsilon )-\upsilon ^{-1}\xi _1(\mathbf {b},\upsilon )\in W_0\mu $
. By Theorem 4.10,
$\upsilon ^{-1}b\xi _1(\mathbf {b},\upsilon )-\upsilon ^{-1}\xi _1(\mathbf {b},\upsilon )\in W_0\mu $
. By Theorem 4.10,
This finishes the proof.
We say that an element
![]() $\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
is cyclic if
$\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
is cyclic if
Now we give another interpretation of Lemma 3.11. Recall that
![]() $\mathbb B_\mu ^*$
is isomorphic to
$\mathbb B_\mu ^*$
is isomorphic to
![]() $\mathbb B_{\mu ^*}$
. We denote by
$\mathbb B_{\mu ^*}$
. We denote by
![]() $\mathbf {b}^*\in \mathbb B_{\mu ^*}$
the dual of
$\mathbf {b}^*\in \mathbb B_{\mu ^*}$
the dual of
![]() $\mathbf {b}\in \mathbb B_\mu $
. Note that we have
$\mathbf {b}\in \mathbb B_\mu $
. Note that we have
![]() $(w\mathbf {b})^*=w\mathbf {b}^*$
for any
$(w\mathbf {b})^*=w\mathbf {b}^*$
for any
![]() $w\in W_0$
. So if
$w\in W_0$
. So if
![]() $\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
, then
$\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
, then
![]() ${\mathbf {b}^{\operatorname {\mathrm {op}}}}^*=w_{\max }\mathbf {b}^*\in \mathbb B_{\mu ^*}(\lambda _{b^*})$
.
${\mathbf {b}^{\operatorname {\mathrm {op}}}}^*=w_{\max }\mathbf {b}^*\in \mathbb B_{\mu ^*}(\lambda _{b^*})$
.
Lemma 4.12 We have
![]() $\lambda ({\mathbf {b}^{\operatorname {\mathrm {op}}}}^*)=-w(\mathbf {b})^{-1}\lambda (\mathbf {b})+(d,\ldots , d)$
. In particular,
$\lambda ({\mathbf {b}^{\operatorname {\mathrm {op}}}}^*)=-w(\mathbf {b})^{-1}\lambda (\mathbf {b})+(d,\ldots , d)$
. In particular,
![]() $\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
is cyclic if and only if
$\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
is cyclic if and only if
![]() ${\mathbf {b}^{\operatorname {\mathrm {op}}}}^*\in \mathbb B_{\mu ^*}(\lambda _{b^*})$
is cyclic.
${\mathbf {b}^{\operatorname {\mathrm {op}}}}^*\in \mathbb B_{\mu ^*}(\lambda _{b^*})$
is cyclic.
Proof Note that if
![]() $(\mu _1,\ldots ,\mu _d)$
is Far-Eastern, then
$(\mu _1,\ldots ,\mu _d)$
is Far-Eastern, then
![]() $(\mu _d^*,\ldots , \mu _1^*)$
is Far-Eastern. So if we write
$(\mu _d^*,\ldots , \mu _1^*)$
is Far-Eastern. So if we write
in
![]() $\mathbb B_{\mu _1}\otimes \cdots \otimes \mathbb B_{\mu _d}$
, then we have
$\mathbb B_{\mu _1}\otimes \cdots \otimes \mathbb B_{\mu _d}$
, then we have
in
![]() $\mathbb B_{\mu _d^*}\otimes \cdots \otimes \mathbb B_{\mu _1^*}$
. Thus
$\mathbb B_{\mu _d^*}\otimes \cdots \otimes \mathbb B_{\mu _1^*}$
. Thus
![]() $w({\mathbf {b}^{\operatorname {\mathrm {op}}}}^*)=w_d\cdots w_1=w(\mathbf {b})^{-1}, \Upsilon ({\mathbf {b}^{\operatorname {\mathrm {op}}}}^*)=\Upsilon (\mathbf {b})$
and
$w({\mathbf {b}^{\operatorname {\mathrm {op}}}}^*)=w_d\cdots w_1=w(\mathbf {b})^{-1}, \Upsilon ({\mathbf {b}^{\operatorname {\mathrm {op}}}}^*)=\Upsilon (\mathbf {b})$
and
 $$ \begin{align*} \lambda({\mathbf{b}^{\operatorname{\mathrm{op}}}}^*)&=\operatorname{\mathrm{wt}}(w_d\mathbf{b}_d^*)+w_d\operatorname{\mathrm{wt}}(w_{d-1}\mathbf{b}_{d-1}^*)+\cdots+w_d\cdots w_2\operatorname{\mathrm{wt}}(w_1\mathbf{b}_1^*)\\ &=-w(\mathbf{b})^{-1}\lambda(\mathbf{b})+(d,\ldots, d), \end{align*} $$
$$ \begin{align*} \lambda({\mathbf{b}^{\operatorname{\mathrm{op}}}}^*)&=\operatorname{\mathrm{wt}}(w_d\mathbf{b}_d^*)+w_d\operatorname{\mathrm{wt}}(w_{d-1}\mathbf{b}_{d-1}^*)+\cdots+w_d\cdots w_2\operatorname{\mathrm{wt}}(w_1\mathbf{b}_1^*)\\ &=-w(\mathbf{b})^{-1}\lambda(\mathbf{b})+(d,\ldots, d), \end{align*} $$
as desired.
4.3 Noncyclic semi-standard tableaux
The goal of this section is to specify the dominant cocharacters
![]() $\mu $
such that every
$\mu $
such that every
![]() $\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
is cyclic. Set
$\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
is cyclic. Set
![]() $d=\mu (1)$
.
$d=\mu (1)$
.
Lemma 4.13 Assume that
![]() $n\geq 3$
. We have
$n\geq 3$
. We have
![]() $d\geq 2\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor +1$
or
$d\geq 2\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor +1$
or
![]() $d\geq 2\lfloor \frac {nd-m}{n}\rfloor +\lfloor \frac {2(n-m_0)}{n}\rfloor +1$
.
$d\geq 2\lfloor \frac {nd-m}{n}\rfloor +\lfloor \frac {2(n-m_0)}{n}\rfloor +1$
.
Proof It suffices to show that
![]() $d\le 2\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor $
is equivalent to
$d\le 2\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor $
is equivalent to
![]() $d\geq 2\lfloor \frac {nd-m}{n}\rfloor +\lfloor \frac {2(n-m_0)}{n}\rfloor +1$
. Note that
$d\geq 2\lfloor \frac {nd-m}{n}\rfloor +\lfloor \frac {2(n-m_0)}{n}\rfloor +1$
. Note that
![]() $\lfloor \frac {m}{n} \rfloor =\frac {m-m_0}{n}, \lfloor \frac {nd-m}{n}\rfloor =\frac {nd-m-(n-m_0)}{n}$
. So
$\lfloor \frac {m}{n} \rfloor =\frac {m-m_0}{n}, \lfloor \frac {nd-m}{n}\rfloor =\frac {nd-m-(n-m_0)}{n}$
. So
![]() $d\le 2\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor $
is equivalent to
$d\le 2\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor $
is equivalent to
![]() $(n-2)d\le 2(m-d-m_0)+n\lfloor \frac {2m_0}{n}\rfloor $
, and
$(n-2)d\le 2(m-d-m_0)+n\lfloor \frac {2m_0}{n}\rfloor $
, and
![]() $d\geq 2\lfloor \frac {nd-m}{n}\rfloor +\lfloor \frac {2(n-m_0)}{n}\rfloor +1$
is equivalent to
$d\geq 2\lfloor \frac {nd-m}{n}\rfloor +\lfloor \frac {2(n-m_0)}{n}\rfloor +1$
is equivalent to
![]() $(n-2)d\le 2(m-d-m_0)+n(1-\lfloor \frac {2(n-m_0)}{n}\rfloor )$
. Then the assertion follows from the fact that
$(n-2)d\le 2(m-d-m_0)+n(1-\lfloor \frac {2(n-m_0)}{n}\rfloor )$
. Then the assertion follows from the fact that
![]() $\lfloor \frac {2m_0}{n}\rfloor =0$
(resp.
$\lfloor \frac {2m_0}{n}\rfloor =0$
(resp.
![]() $1$
) if and only if
$1$
) if and only if
![]() $\lfloor \frac {2(n-m_0)}{n}\rfloor =1$
(resp.
$\lfloor \frac {2(n-m_0)}{n}\rfloor =1$
(resp.
![]() $0$
).
$0$
).
Lemma 4.14 Assume that
![]() $n\geq 3$
. Let
$n\geq 3$
. Let
![]() $\mu \in X_*(T)_+$
such that
$\mu \in X_*(T)_+$
such that
![]() $d\geq 2\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor +1, \mu (2)\geq 2$
and
$d\geq 2\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor +1, \mu (2)\geq 2$
and
![]() $\lfloor \frac {m}{n} \rfloor \geq 2$
. Then
$\lfloor \frac {m}{n} \rfloor \geq 2$
. Then
![]() $\mathbb B_\mu (\lambda _b)$
contains at least one noncyclic element.
$\mathbb B_\mu (\lambda _b)$
contains at least one noncyclic element.
Proof First we consider the case
![]() $n=3$
. In this case, we have
$n=3$
. In this case, we have
![]() $2\le \mu (2)\le \lfloor \frac {m}{n} \rfloor $
because
$2\le \mu (2)\le \lfloor \frac {m}{n} \rfloor $
because
![]() $\mu (3)=0$
. Let
$\mu (3)=0$
. Let
![]() $\mathbf {b}$
be the unique element in
$\mathbf {b}$
be the unique element in
![]() $\mathbb B_\mu (\lambda _b)$
whose second row contains exactly one
$\mathbb B_\mu (\lambda _b)$
whose second row contains exactly one
![]() $\fbox{3}$
. Then
$\fbox{3}$
. Then
![]() $w(\mathbf {b})=s_2s_1$
and
$w(\mathbf {b})=s_2s_1$
and
![]() $s_1\in \operatorname {\mathrm {supp}}(w_{d-\lfloor \frac {m}{n} \rfloor })$
.
$s_1\in \operatorname {\mathrm {supp}}(w_{d-\lfloor \frac {m}{n} \rfloor })$
.

Since
![]() $2\le \mu (2)\le \lfloor \frac {m}{n} \rfloor $
, we have
$2\le \mu (2)\le \lfloor \frac {m}{n} \rfloor $
, we have
Thus
![]() $\lambda (\mathbf {b})\notin W_0\mu $
because
$\lambda (\mathbf {b})\notin W_0\mu $
because
![]() $\mu (n)=0$
. This proves the case
$\mu (n)=0$
. This proves the case
![]() $n=3$
.
$n=3$
.
In the rest of the proof, we assume that
![]() $n\geq 4$
. Let
$n\geq 4$
. Let
![]() $\lambda $
be a conjugate of
$\lambda $
be a conjugate of
![]() $\lambda _b$
such that
$\lambda _b$
such that
![]() $(\lambda (1),\lambda (2),\lambda (3))=(\lfloor \frac {m}{n} \rfloor , \lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor , \lfloor \frac {m}{n} \rfloor +1)$
and
$(\lambda (1),\lambda (2),\lambda (3))=(\lfloor \frac {m}{n} \rfloor , \lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor , \lfloor \frac {m}{n} \rfloor +1)$
and
![]() $\lambda (4)\geq \cdots \geq \lambda (n)$
. Set
$\lambda (4)\geq \cdots \geq \lambda (n)$
. Set
and
![]() $\lambda _0=(\lambda (1),\lambda (2),\lambda (3),0,\ldots , 0)\in X_*(T)$
. Note that we have
$\lambda _0=(\lambda (1),\lambda (2),\lambda (3),0,\ldots , 0)\in X_*(T)$
. Note that we have
![]() $\mu (1)+\mu (2)\geq 3\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor +1$
. Indeed if
$\mu (1)+\mu (2)\geq 3\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor +1$
. Indeed if
![]() $\mu (1)+\mu (2)\le 3\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor $
, then by
$\mu (1)+\mu (2)\le 3\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor $
, then by
![]() $\mu (1)\geq 2\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor +1$
, we have
$\mu (1)\geq 2\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor +1$
, we have
![]() $\mu (2)\le \lfloor \frac {m}{n} \rfloor -1$
. This implies
$\mu (2)\le \lfloor \frac {m}{n} \rfloor -1$
. This implies
![]() $\mu (3)+\cdots +\mu (n-1)\le (n-3)(\lfloor \frac {m}{n} \rfloor -1)$
, or equivalently
$\mu (3)+\cdots +\mu (n-1)\le (n-3)(\lfloor \frac {m}{n} \rfloor -1)$
, or equivalently
![]() $3\lfloor \frac {m}{n} \rfloor +n+m_0-3\le \mu (1)+\mu (2)$
, which is a contradiction. Thus
$3\lfloor \frac {m}{n} \rfloor +n+m_0-3\le \mu (1)+\mu (2)$
, which is a contradiction. Thus
![]() $Y_\mu $
contains
$Y_\mu $
contains
![]() $Y_{\mu _0}$
.
$Y_{\mu _0}$
.
Let
![]() $\mathbf {b}_0$
be the unique element in
$\mathbf {b}_0$
be the unique element in
![]() $\mathbb B_{\mu _0}(\lambda _0)$
whose second row contains exactly one
$\mathbb B_{\mu _0}(\lambda _0)$
whose second row contains exactly one
![]() $\fbox{3}$
. We will show that there exists
$\fbox{3}$
. We will show that there exists
![]() $\mathbf {b}'\in \mathbb B_\mu (\lambda )$
that contains
$\mathbf {b}'\in \mathbb B_\mu (\lambda )$
that contains
![]() $\mathbf {b}_0$
. It is easy to check that
$\mathbf {b}_0$
. It is easy to check that
![]() $\mu (n-1)\le \lfloor \frac {m}{n} \rfloor $
and
$\mu (n-1)\le \lfloor \frac {m}{n} \rfloor $
and
![]() $\mu (n-2)\le \mu _0(1)$
. So each column in
$\mu (n-2)\le \mu _0(1)$
. So each column in
![]() $Y_{\mu /\mu _0}$
has at most
$Y_{\mu /\mu _0}$
has at most
![]() $n-3$
boxes. By filling each column with the numbers
$n-3$
boxes. By filling each column with the numbers
![]() $1,\ldots , n-3$
so that the entries are starting with
$1,\ldots , n-3$
so that the entries are starting with
![]() $1$
and increasing by one from top to bottom, we obtain a skew Young tableau of shape
$1$
and increasing by one from top to bottom, we obtain a skew Young tableau of shape
![]() $Y_{\mu /\mu _0}$
. Let
$Y_{\mu /\mu _0}$
. Let
![]() $k_i$
be the number of
$k_i$
be the number of
![]() $\fbox{$i$}$
in this tableau. Clearly we have
$\fbox{$i$}$
in this tableau. Clearly we have
![]() $k_1\geq \cdots \geq k_{n-3}$
.
$k_1\geq \cdots \geq k_{n-3}$
.

By
![]() $(\lambda (4),\ldots ,\lambda (n))\preceq (k_1,\ldots , k_{n-3})$
and Proposition 4.5, there exists at least one skew Young tableau of shape
$(\lambda (4),\ldots ,\lambda (n))\preceq (k_1,\ldots , k_{n-3})$
and Proposition 4.5, there exists at least one skew Young tableau of shape
![]() $Y_{\mu /\mu _0}$
such that the number of
$Y_{\mu /\mu _0}$
such that the number of
![]() $\fbox{$i$}$
is
$\fbox{$i$}$
is
![]() $\lambda (i+3)$
for each
$\lambda (i+3)$
for each
![]() $1\le i\le n-3$
. By replacing
$1\le i\le n-3$
. By replacing
![]() $1,\ldots , n-3$
by
$1,\ldots , n-3$
by
![]() $4,\ldots ,n$
respectively, we obtain a skew Young tableau of shape
$4,\ldots ,n$
respectively, we obtain a skew Young tableau of shape
![]() $Y_{\mu /\mu _0}$
such that the number of
$Y_{\mu /\mu _0}$
such that the number of
![]() $\fbox{$i$}$
is
$\fbox{$i$}$
is
![]() $\lambda (i)$
for each
$\lambda (i)$
for each
![]() $4\le i\le n$
. Let
$4\le i\le n$
. Let
![]() $\mathbf {b}'$
be the tableau obtained by joining
$\mathbf {b}'$
be the tableau obtained by joining
![]() $\mathbf {b}_0$
and this skew tableau. Clearly we have
$\mathbf {b}_0$
and this skew tableau. Clearly we have
![]() $\mathbf {b}'\in \mathbb B_\mu (\lambda )$
, which shows our claim.
$\mathbf {b}'\in \mathbb B_\mu (\lambda )$
, which shows our claim.
Let
![]() $\mathbf {b}'\in \mathbb B_\mu (\lambda )$
containing
$\mathbf {b}'\in \mathbb B_\mu (\lambda )$
containing
![]() $\mathbf {b}_0$
, and let
$\mathbf {b}_0$
, and let
![]() $\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
be the conjugate of
$\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
be the conjugate of
![]() $\mathbf {b}'$
. Then
$\mathbf {b}'$
. Then
![]() $s_2s_1\le w(\mathbf {b})$
and
$s_2s_1\le w(\mathbf {b})$
and
![]() $s_1\in \operatorname {\mathrm {supp}}(w_{d-\lfloor \frac {m}{n} \rfloor })$
. Let
$s_1\in \operatorname {\mathrm {supp}}(w_{d-\lfloor \frac {m}{n} \rfloor })$
. Let
![]() $k(\mathbf {b}')$
be the number of
$k(\mathbf {b}')$
be the number of
![]() $\fbox{4}$
in the second row of
$\fbox{4}$
in the second row of
![]() $\mathbf {b}'$
. If
$\mathbf {b}'$
. If
![]() $k(\mathbf {b}')<\lfloor \frac {m}{n} \rfloor $
, then we have
$k(\mathbf {b}')<\lfloor \frac {m}{n} \rfloor $
, then we have
and
Thus,
![]() $\lambda (\mathbf {b})\notin W_0\mu $
and hence
$\lambda (\mathbf {b})\notin W_0\mu $
and hence
![]() $\mathbf {b}$
is noncyclic. If
$\mathbf {b}$
is noncyclic. If
![]() $k(\mathbf {b}')\neq 0$
, then
$k(\mathbf {b}')\neq 0$
, then
![]() $\lambda (\mathbf {b})(1)=\lfloor \frac {m}{n} \rfloor -1$
.
$\lambda (\mathbf {b})(1)=\lfloor \frac {m}{n} \rfloor -1$
.
Assume that
![]() $\mu (3)<\lfloor \frac {m}{n} \rfloor -1$
. Then
$\mu (3)<\lfloor \frac {m}{n} \rfloor -1$
. Then
![]() $\mathbf {b}$
is always noncyclic by the above argument.
$\mathbf {b}$
is always noncyclic by the above argument.
Assume that
![]() $\mu (3)\geq 2$
. Let
$\mu (3)\geq 2$
. Let
![]() $\mathbf {b}^{\prime }_1=$
$\mathbf {b}^{\prime }_1=$
![]() $\fbox{$j$}$
be the leftmost box in the third row of
$\fbox{$j$}$
be the leftmost box in the third row of
![]() $\mathbf {b}'$
, and let
$\mathbf {b}'$
, and let
![]() $\mathbf {b}^{\prime }_2=$
$\mathbf {b}^{\prime }_2=$
![]() $\fbox{$j$'}$
be the box right to
$\fbox{$j$'}$
be the box right to
![]() $\mathbf {b}^{\prime }_1$
. Clearly
$\mathbf {b}^{\prime }_1$
. Clearly
![]() $4\le j\le j'$
.
$4\le j\le j'$
.

Then in
![]() $\mathbf {b}'$
, all
$\mathbf {b}'$
, all
![]() $\fbox{$j-$1}$
are in the first or second row. Since the number of
$\fbox{$j-$1}$
are in the first or second row. Since the number of
![]() $\fbox{$j$}$
in the first or second row is less than
$\fbox{$j$}$
in the first or second row is less than
![]() $\operatorname {\mathrm {wt}}(\mathbf {b}')(j-1)$
, there exists at least one
$\operatorname {\mathrm {wt}}(\mathbf {b}')(j-1)$
, there exists at least one
![]() $\fbox{$j-$1}$
such that there is no box beneath it or the number in the box beneath it is greater than j. So the tableau obtained by replacing
$\fbox{$j-$1}$
such that there is no box beneath it or the number in the box beneath it is greater than j. So the tableau obtained by replacing
![]() $\mathbf {b}^{\prime }_1$
by the rightmost one among such
$\mathbf {b}^{\prime }_1$
by the rightmost one among such
![]() $\fbox{$j-$1}$
is semi-standard. Repeating the same argument, we may assume
$\fbox{$j-$1}$
is semi-standard. Repeating the same argument, we may assume
![]() $j=4$
. Similarly, if
$j=4$
. Similarly, if
![]() $\lfloor \frac {m}{n} \rfloor \geq 3$
, we may also assume
$\lfloor \frac {m}{n} \rfloor \geq 3$
, we may also assume
![]() $j'=4$
. Indeed if
$j'=4$
. Indeed if
![]() $j'\geq 6$
and the leftmost column in
$j'\geq 6$
and the leftmost column in
![]() $\mathbf {b}'$
contains
$\mathbf {b}'$
contains
![]() $\fbox{$j$'$-$1}$
but does not contain
$\fbox{$j$'$-$1}$
but does not contain
![]() $\fbox{$j$'}$
, we replace
$\fbox{$j$'}$
, we replace
![]() $\mathbf {b}^{\prime }_2$
by this
$\mathbf {b}^{\prime }_2$
by this
![]() $\fbox{$j$'$-$1}$
. In other cases, by
$\fbox{$j$'$-$1}$
. In other cases, by
![]() $\lfloor \frac {m}{n} \rfloor \geq 3$
, there exists at least one
$\lfloor \frac {m}{n} \rfloor \geq 3$
, there exists at least one
![]() $\fbox{$j$'$-$1}$
such that there is no box beneath it or the number in the box beneath it is greater than
$\fbox{$j$'$-$1}$
such that there is no box beneath it or the number in the box beneath it is greater than
![]() $j'$
, and we replace
$j'$
, and we replace
![]() $\mathbf {b}^{\prime }_2$
by the rightmost
$\mathbf {b}^{\prime }_2$
by the rightmost
![]() $\fbox{$j$'$-$1}$
among such
$\fbox{$j$'$-$1}$
among such
![]() $\fbox{$j$'$-$1}$
. Then the obtained tableau is semi-standard. Thus, if
$\fbox{$j$'$-$1}$
. Then the obtained tableau is semi-standard. Thus, if
![]() $\lfloor \frac {m}{n} \rfloor \geq 3$
, there exists
$\lfloor \frac {m}{n} \rfloor \geq 3$
, there exists
![]() $\mathbf {b}'$
containing
$\mathbf {b}'$
containing
![]() $\mathbf {b}_0$
such that
$\mathbf {b}_0$
such that
![]() $k(\mathbf {b}')<\lfloor \frac {m}{n} \rfloor $
, which is noncyclic by the above argument. If
$k(\mathbf {b}')<\lfloor \frac {m}{n} \rfloor $
, which is noncyclic by the above argument. If
![]() $\lfloor \frac {m}{n} \rfloor =2$
and
$\lfloor \frac {m}{n} \rfloor =2$
and
![]() $n=4$
, then
$n=4$
, then
![]() $\mathbf {b}$
is noncyclic because
$\mathbf {b}$
is noncyclic because
![]() $k(\mathbf {b}')<2$
. If
$k(\mathbf {b}')<2$
. If
![]() $\lfloor \frac {m}{n} \rfloor =2$
and
$\lfloor \frac {m}{n} \rfloor =2$
and
![]() $n\geq 5$
, we may also assume
$n\geq 5$
, we may also assume
![]() $j'=4$
and hence
$j'=4$
and hence
![]() $\mathbf {b}$
is noncyclic unless the third row of
$\mathbf {b}$
is noncyclic unless the third row of
![]() $\mathbf {b}'$
contains three
$\mathbf {b}'$
contains three
![]() $\fbox{5}$
. If
$\fbox{5}$
. If
![]() $\lfloor \frac {m}{n} \rfloor =2, n\geq 5$
and the third row of
$\lfloor \frac {m}{n} \rfloor =2, n\geq 5$
and the third row of
![]() $\mathbf {b}'$
contains three
$\mathbf {b}'$
contains three
![]() $\fbox{5}$
, then
$\fbox{5}$
, then
Thus,
![]() $\lambda (\mathbf {b})\notin W_0\mu $
and hence
$\lambda (\mathbf {b})\notin W_0\mu $
and hence
![]() $\mathbf {b}$
is noncyclic.
$\mathbf {b}$
is noncyclic.

Assume that
![]() $\lfloor \frac {m}{n} \rfloor =2$
and
$\lfloor \frac {m}{n} \rfloor =2$
and
![]() $\mu (3)=1$
. By the same argument as above, we may assume that the leftmost column of
$\mu (3)=1$
. By the same argument as above, we may assume that the leftmost column of
![]() $\mathbf {b}'$
contains
$\mathbf {b}'$
contains
![]() $\fbox{4}$
. So
$\fbox{4}$
. So
![]() $\mathbf {b}$
is noncyclic when
$\mathbf {b}$
is noncyclic when
![]() $\lambda (4)=2$
. If
$\lambda (4)=2$
. If
![]() $\mu (1)> 5+\lfloor \frac {2m_0}{n}\rfloor $
, we may assume that the first row of
$\mu (1)> 5+\lfloor \frac {2m_0}{n}\rfloor $
, we may assume that the first row of
![]() $\mathbf {b}'$
also contains
$\mathbf {b}'$
also contains
![]() $\fbox{4}$
. This can be checked easily as above using
$\fbox{4}$
. This can be checked easily as above using
![]() $\mu (3)=1$
. Thus, if
$\mu (3)=1$
. Thus, if
![]() $\mu (1)> 5+\lfloor \frac {2m_0}{n}\rfloor $
, we obtain a noncyclic
$\mu (1)> 5+\lfloor \frac {2m_0}{n}\rfloor $
, we obtain a noncyclic
![]() $\mathbf {b}$
.
$\mathbf {b}$
.

If
![]() $\mu (1)= 5+\lfloor \frac {2m_0}{n}\rfloor $
, then we have
$\mu (1)= 5+\lfloor \frac {2m_0}{n}\rfloor $
, then we have
![]() $n=4$
or
$n=4$
or
![]() $5$
. More precisely, we have
$5$
. More precisely, we have
and
![]() $\mathbf {b}'$
contains one of the following smaller Young tableaux when
$\mathbf {b}'$
contains one of the following smaller Young tableaux when
![]() $\lambda (4)=3$
.
$\lambda (4)=3$
.

We can easily check that
![]() $\mathbf {b}$
is noncyclic in every case.
$\mathbf {b}$
is noncyclic in every case.
Putting things together, we have proved the lemma.
Lemma 4.15 Assume that
![]() $n\geq 4$
. Let
$n\geq 4$
. Let
![]() $\mu \in X_*(T)_+$
such that
$\mu \in X_*(T)_+$
such that
![]() $d\geq 3+\lfloor \frac {2m_0}{n}\rfloor , \mu (2)\geq 2$
and
$d\geq 3+\lfloor \frac {2m_0}{n}\rfloor , \mu (2)\geq 2$
and
![]() $\lfloor \frac {m}{n} \rfloor =1$
. Then
$\lfloor \frac {m}{n} \rfloor =1$
. Then
![]() $\mathbb B_\mu (\lambda _b)$
contains at least one noncyclic element.
$\mathbb B_\mu (\lambda _b)$
contains at least one noncyclic element.
Proof Let
![]() $\lambda $
be a conjugate of
$\lambda $
be a conjugate of
![]() $\lambda _b$
such that
$\lambda _b$
such that
![]() $(\lambda (1),\lambda (2),\lambda (3))=(\lambda _b(1),\lambda _b(2),\lambda _b(3))$
and
$(\lambda (1),\lambda (2),\lambda (3))=(\lambda _b(1),\lambda _b(2),\lambda _b(3))$
and
![]() $\lambda (4)\geq \cdots \geq \lambda (n)$
. Assume that
$\lambda (4)\geq \cdots \geq \lambda (n)$
. Assume that
![]() $(\lambda _b(1),\lambda _b(2),\lambda _b(3))=(1,2,2)$
and
$(\lambda _b(1),\lambda _b(2),\lambda _b(3))=(1,2,2)$
and
![]() $\mu (2)\geq 3$
. Similarly as the proof of Lemma 4.14, we can easily show that there exists
$\mu (2)\geq 3$
. Similarly as the proof of Lemma 4.14, we can easily show that there exists
![]() $\mathbf {b}'\in \mathbb B_\mu (\lambda )$
containing the following smaller Young tableau.
$\mathbf {b}'\in \mathbb B_\mu (\lambda )$
containing the following smaller Young tableau.

Let
![]() $\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
be the conjugate of
$\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
be the conjugate of
![]() $\mathbf {b}'$
. If
$\mathbf {b}'$
. If
![]() $\mu (3)<2$
, then
$\mu (3)<2$
, then
![]() $\mathbf {b}$
is noncyclic because
$\mathbf {b}$
is noncyclic because
![]() $\lambda (\mathbf {b})(2)=2$
. If
$\lambda (\mathbf {b})(2)=2$
. If
![]() $\mu (3)\geq 2$
, then similarly as the proof of Lemma 4.14, we may assume that the second row of
$\mu (3)\geq 2$
, then similarly as the proof of Lemma 4.14, we may assume that the second row of
![]() $\mathbf {b}'$
does not contain
$\mathbf {b}'$
does not contain
![]() $\fbox{5}$
. In this case, the conjugate
$\fbox{5}$
. In this case, the conjugate
![]() $\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
of
$\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
of
![]() $\mathbf {b}'$
is noncyclic because
$\mathbf {b}'$
is noncyclic because
Assume that
![]() $(\lambda _b(1),\lambda _b(2),\lambda _b(3))=(1,2,2)$
and
$(\lambda _b(1),\lambda _b(2),\lambda _b(3))=(1,2,2)$
and
![]() $\mu (2)=2$
. Then there exists
$\mu (2)=2$
. Then there exists
![]() $\mathbf {b}'\in \mathbb B_\mu (\lambda )$
containing one of the following smaller Young tableaux.
$\mathbf {b}'\in \mathbb B_\mu (\lambda )$
containing one of the following smaller Young tableaux.

It is easy to check that the conjugate
![]() $\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
of
$\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
of
![]() $\mathbf {b}'$
is noncyclic.
$\mathbf {b}'$
is noncyclic.
Assume that
![]() $(\lambda _b(1),\lambda _b(2),\lambda _b(3))\neq (1,2,2)$
. Then there exists
$(\lambda _b(1),\lambda _b(2),\lambda _b(3))\neq (1,2,2)$
. Then there exists
![]() $\mathbf {b}'\in \mathbb B_\mu (\lambda )$
containing one of the following smaller Young tableaux.
$\mathbf {b}'\in \mathbb B_\mu (\lambda )$
containing one of the following smaller Young tableaux.

Let
![]() $\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
be the conjugate of
$\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
be the conjugate of
![]() $\mathbf {b}'$
. Since
$\mathbf {b}'$
. Since
![]() $\lambda (\mathbf {b})(1)=1$
,
$\lambda (\mathbf {b})(1)=1$
,
![]() $\mathbf {b}$
is noncyclic if
$\mathbf {b}$
is noncyclic if
![]() $\mu (3)=0$
. If
$\mu (3)=0$
. If
![]() $\mu (3)\geq 2$
, then similarly as the proof of Lemma 4.14, we may assume that the second row of
$\mu (3)\geq 2$
, then similarly as the proof of Lemma 4.14, we may assume that the second row of
![]() $\mathbf {b}'$
does not contain
$\mathbf {b}'$
does not contain
![]() $\fbox{5}$
. In this case,
$\fbox{5}$
. In this case,
![]() $\mathbf {b}$
is noncyclic because
$\mathbf {b}$
is noncyclic because
If
![]() $\mu (3)=1$
and
$\mu (3)=1$
and
![]() $\mu (1)>3+\lfloor \frac {2m_0}{n}\rfloor $
, then we may also assume that the second row of
$\mu (1)>3+\lfloor \frac {2m_0}{n}\rfloor $
, then we may also assume that the second row of
![]() $\mathbf {b}'$
does not contain
$\mathbf {b}'$
does not contain
![]() $\fbox{5}$
and hence
$\fbox{5}$
and hence
![]() $\mathbf {b}$
is noncyclic. If
$\mathbf {b}$
is noncyclic. If
![]() $\mu (3)=1$
and
$\mu (3)=1$
and
![]() $\mu (1)=3+\lfloor \frac {2m_0}{n}\rfloor $
, then we may assume that the leftmost column of
$\mu (1)=3+\lfloor \frac {2m_0}{n}\rfloor $
, then we may assume that the leftmost column of
![]() $\mathbf {b}'$
contains
$\mathbf {b}'$
contains
![]() $\fbox{5}$
. We can easily check that
$\fbox{5}$
. We can easily check that
![]() $\mathbf {b}$
is noncyclic by an easy calculation.
$\mathbf {b}$
is noncyclic by an easy calculation.

This finishes the proof.
Lemma 4.16 Assume that
![]() $n\geq 5$
. Let
$n\geq 5$
. Let
![]() $\mu \in X_*(T)_+$
such that
$\mu \in X_*(T)_+$
such that
![]() $\lfloor \frac {m}{n} \rfloor =0$
. If
$\lfloor \frac {m}{n} \rfloor =0$
. If
![]() $(1)\ \mu (2)\geq 2$
or
$(1)\ \mu (2)\geq 2$
or
![]() $(2)\ d\geq 3, \mu (2)=1$
, then
$(2)\ d\geq 3, \mu (2)=1$
, then
![]() $\mathbb B_\mu (\lambda _b)$
contains at least one noncyclic element.
$\mathbb B_\mu (\lambda _b)$
contains at least one noncyclic element.
Proof Let
![]() $1<i_1<i_2<\cdots <i_{m_0}=n$
be the integers such that
$1<i_1<i_2<\cdots <i_{m_0}=n$
be the integers such that
![]() $\lambda _b(i_1)=\lambda _b(i_2)=\cdots =\lambda _b(i_{m_0})=1$
. Let
$\lambda _b(i_1)=\lambda _b(i_2)=\cdots =\lambda _b(i_{m_0})=1$
. Let
![]() $\mathbf {b}$
be the Young tableau in
$\mathbf {b}$
be the Young tableau in
![]() $\mathbb B_\mu (\lambda _b)$
obtained by filling
$\mathbb B_\mu (\lambda _b)$
obtained by filling
![]() $Y_\mu $
with
$Y_\mu $
with
![]() $i_1,\ldots , i_{m_0}$
from top to bottom, starting from the leftmost column.
$i_1,\ldots , i_{m_0}$
from top to bottom, starting from the leftmost column.

If (1) holds, then
![]() $\mathbf {b}$
is noncyclic because
$\mathbf {b}$
is noncyclic because
Let
![]() $k=\max \{i\mid \mu (i)\neq 0\}$
. If (2) holds, then the Young tableau
$k=\max \{i\mid \mu (i)\neq 0\}$
. If (2) holds, then the Young tableau
![]() $\mathbf c\in \mathbb B_\mu (\lambda _b)$
obtained by replacing
$\mathbf c\in \mathbb B_\mu (\lambda _b)$
obtained by replacing
![]() ${i_k}$
by
${i_k}$
by
![]() ${i_{k+1}}$
in
${i_{k+1}}$
in
![]() $\mathbf {b}$
is noncyclic because
$\mathbf {b}$
is noncyclic because
![]() $\lambda (\mathbf c)(i_k)=2$
.
$\lambda (\mathbf c)(i_k)=2$
.

This finishes the proof.
Theorem 4.17 Every
![]() $\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
is cyclic if and only if
$\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
is cyclic if and only if
![]() $\mu $
has one of the following forms:
$\mu $
has one of the following forms:
-
(i)
 $\omega _i$
with
$\omega _i$
with
 $1\le i\le n-1$
such that i is coprime to n.
$1\le i\le n-1$
such that i is coprime to n. -
(ii)
 $\omega _1+\omega _i$
or
$\omega _1+\omega _i$
or
 $\omega _{n-1}+\omega _{n-i}$
with
$\omega _{n-1}+\omega _{n-i}$
with
 $1\le i\le n-1$
such that
$1\le i\le n-1$
such that
 $i+1$
is coprime to n.
$i+1$
is coprime to n. -
(iii)
 $(nr+i)\omega _1$
or
$(nr+i)\omega _1$
or
 $(nr+i)\omega _{n-1}$
with
$(nr+i)\omega _{n-1}$
with
 $r\geq 0$
and
$r\geq 0$
and
 $1\le i\le n-1$
such that i is coprime to n.
$1\le i\le n-1$
such that i is coprime to n. -
(iv)
 $(nr+i-j)\omega _1+\omega _j$
or
$(nr+i-j)\omega _1+\omega _j$
or
 $(nr+i-j)\omega _{n-1}+\omega _{n-j}$
with
$(nr+i-j)\omega _{n-1}+\omega _{n-j}$
with
 $r\geq 1$
,
$r\geq 1$
,
 $2\le j\le n-1$
and
$2\le j\le n-1$
and
 $1\le i\le n-1$
such that i is coprime to n.
$1\le i\le n-1$
such that i is coprime to n.
Proof It is easy to check that every
![]() $\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
is cyclic if
$\mathbf {b}\in \mathbb B_\mu (\lambda _b)$
is cyclic if
![]() $\mu $
is one of the cocharacters in (i), (ii), (iii) and (iv). It remains to show that if
$\mu $
is one of the cocharacters in (i), (ii), (iii) and (iv). It remains to show that if
![]() $\mu $
does not belong to the list above, then
$\mu $
does not belong to the list above, then
![]() $\mathbb B_\mu (\lambda _b)$
contains at least one noncyclic element. By Lemmas 4.12 and 4.13, we may assume that
$\mathbb B_\mu (\lambda _b)$
contains at least one noncyclic element. By Lemmas 4.12 and 4.13, we may assume that
![]() $d\geq 2\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor +1$
. Then this follows from Lemmas 4.14, 4.15 and 4.16.
$d\geq 2\lfloor \frac {m}{n} \rfloor +\lfloor \frac {2m_0}{n}\rfloor +1$
. Then this follows from Lemmas 4.14, 4.15 and 4.16.
Remark 4.18 Even if every top extended semi-module for
![]() $\mu $
is cyclic, there might be a noncyclic extended semi-module for
$\mu $
is cyclic, there might be a noncyclic extended semi-module for
![]() $\mu $
. In fact, such cases exist, see Section 5.4.
$\mu $
. In fact, such cases exist, see Section 5.4.
5 The semi-module stratification
Keep the notations and assumptions in Section 3.
5.1 The semi-module stratification for
 $\omega _i$
$\omega _i$
Recall that if
![]() $\mu $
is minuscule, then every extended semi-module is cyclic.
$\mu $
is minuscule, then every extended semi-module is cyclic.
Lemma 5.1 For any
![]() $1\le j\le \frac {n-3}{2}(=\dim X_{\omega _2}(\tau ^2))$
, we have
$1\le j\le \frac {n-3}{2}(=\dim X_{\omega _2}(\tau ^2))$
, we have
 $$ \begin{align*}\mathbb A_{\omega_2}^j= \begin{cases} \{[\chi_{2,n-1}^\vee+\chi_{4,n-3}^\vee+\cdots+\chi_{j,n-j+1}^\vee]\} & (j\ \mathrm{even})\\ \{[\chi_{1,n}^\vee+\chi_{3,n-2}^\vee+\cdots+\chi_{j,n-j+1}^\vee]\} & (j\ \mathrm{odd}). \end{cases}\end{align*} $$
$$ \begin{align*}\mathbb A_{\omega_2}^j= \begin{cases} \{[\chi_{2,n-1}^\vee+\chi_{4,n-3}^\vee+\cdots+\chi_{j,n-j+1}^\vee]\} & (j\ \mathrm{even})\\ \{[\chi_{1,n}^\vee+\chi_{3,n-2}^\vee+\cdots+\chi_{j,n-j+1}^\vee]\} & (j\ \mathrm{odd}). \end{cases}\end{align*} $$
Proof By (the proof of) [Reference Viehmann43, Proposition 5.5], each normalized semi-module for
![]() $2,n$
is of the form
$2,n$
is of the form
![]() $A_j=(2\mathbb N-j)\cup (\mathbb N+j+1)$
for some
$A_j=(2\mathbb N-j)\cup (\mathbb N+j+1)$
for some
![]() $1\le j\le \frac {n-3}{2}$
. It is easy to check that
$1\le j\le \frac {n-3}{2}$
. It is easy to check that
 $$ \begin{align*}A_j= \begin{cases} A^{\chi_{2,n-1}^\vee+\chi_{4,n-3}^\vee+\cdots+\chi_{j,n-j+1}^\vee} & (j\ \text{even})\\ A^{\chi_{1,n}^\vee+\chi_{3,n-2}^\vee+\cdots+\chi_{j,n-j+1}^\vee} & (j\ \text{odd}). \end{cases}\end{align*} $$
$$ \begin{align*}A_j= \begin{cases} A^{\chi_{2,n-1}^\vee+\chi_{4,n-3}^\vee+\cdots+\chi_{j,n-j+1}^\vee} & (j\ \text{even})\\ A^{\chi_{1,n}^\vee+\chi_{3,n-2}^\vee+\cdots+\chi_{j,n-j+1}^\vee} & (j\ \text{odd}). \end{cases}\end{align*} $$
Let
![]() $(A_j,\varphi _j)$
be the cyclic semi-module for
$(A_j,\varphi _j)$
be the cyclic semi-module for
![]() $\omega _2$
. Then
$\omega _2$
. Then
![]() $n-2-j,n-1+j\in \bar {A_j}$
and
$n-2-j,n-1+j\in \bar {A_j}$
and
![]() $\varphi _j(n-2-j)=\varphi _j(n-1+j)=1$
. It is also easy to check that
$\varphi _j(n-2-j)=\varphi _j(n-1+j)=1$
. It is also easy to check that
![]() $|\mathcal V(A_j,\varphi _j)|=j$
. This finishes the proof.
$|\mathcal V(A_j,\varphi _j)|=j$
. This finishes the proof.
Lemma 5.2 Assume that
![]() $n=7$
. Then
$n=7$
. Then
![]() $\dim X_{\omega _3}(\tau ^3)=3$
and
$\dim X_{\omega _3}(\tau ^3)=3$
and
Assume that
![]() $n=8$
. Then
$n=8$
. Then
![]() $\dim X_{\omega _3}(\tau ^3)=4$
and
$\dim X_{\omega _3}(\tau ^3)=4$
and
 $$ \begin{align*} \mathbb A_{\omega_3}^1=\{[\chi_{1,8}^\vee]\},\quad &\mathbb A_{\omega_3}^2=\{[\chi_{1,7}^\vee],[\chi_{2,8}^\vee]\},\\ \mathbb A_{\omega_3}^3=\{[\chi_{2,6}^\vee],[\chi_{3,7}^\vee]\},\quad &\mathbb A_{\omega_3}^4=\{[\chi_{1,8}^\vee+\chi_{4,5}^\vee]\}. \end{align*} $$
$$ \begin{align*} \mathbb A_{\omega_3}^1=\{[\chi_{1,8}^\vee]\},\quad &\mathbb A_{\omega_3}^2=\{[\chi_{1,7}^\vee],[\chi_{2,8}^\vee]\},\\ \mathbb A_{\omega_3}^3=\{[\chi_{2,6}^\vee],[\chi_{3,7}^\vee]\},\quad &\mathbb A_{\omega_3}^4=\{[\chi_{1,8}^\vee+\chi_{4,5}^\vee]\}. \end{align*} $$
Proof Using Lemma 3.2, we can easily check the lemma by an easy calculation.
5.2 The semi-module stratification for
 $\omega _1+\omega _{n-2}$
$\omega _1+\omega _{n-2}$
Throughout this subsection, we set
![]() $\mu =\omega _1+\omega _{n-2}$
. Also we assume that
$\mu =\omega _1+\omega _{n-2}$
. Also we assume that
![]() $n\geq 4$
.
$n\geq 4$
.
Lemma 5.3 Every extended semi-module for
![]() $\mu $
is cyclic. For any
$\mu $
is cyclic. For any
![]() $0\le j\le n-2(=\dim X_{\mu }(b))$
, we define
$0\le j\le n-2(=\dim X_{\mu }(b))$
, we define
![]() $\mathbb A_\mu ^j$
similarly as in Section 3.3. Then we have
$\mathbb A_\mu ^j$
similarly as in Section 3.3. Then we have
![]() $\mathbb A_\mu ^0=\emptyset $
and
$\mathbb A_\mu ^0=\emptyset $
and
![]() $|\mathbb A_\mu ^j|=j$
. More precisely, if j is odd, then
$|\mathbb A_\mu ^j|=j$
. More precisely, if j is odd, then
![]() $\mathbb A_\mu ^j$
is equal to
$\mathbb A_\mu ^j$
is equal to
 $$ \begin{align*} \{[\chi_{1,n-j+1}^\vee],&[\chi_{1,n-j+3}^\vee+\chi_{2,n-j+2}^\vee],\ldots,\\ &[\chi_{1,n}^\vee+\chi_{2,n-1}^\vee+\cdots+\chi_{\frac{j+1}{2},n-\frac{j-1}{2}}^\vee],\ldots, [\chi_{j-2,n}^\vee+\chi_{j-1,n-1}^\vee],[\chi_{j,n}^\vee]\}, \end{align*} $$
$$ \begin{align*} \{[\chi_{1,n-j+1}^\vee],&[\chi_{1,n-j+3}^\vee+\chi_{2,n-j+2}^\vee],\ldots,\\ &[\chi_{1,n}^\vee+\chi_{2,n-1}^\vee+\cdots+\chi_{\frac{j+1}{2},n-\frac{j-1}{2}}^\vee],\ldots, [\chi_{j-2,n}^\vee+\chi_{j-1,n-1}^\vee],[\chi_{j,n}^\vee]\}, \end{align*} $$
and if j is even, then
![]() $\mathbb A_\mu ^j$
is equal to
$\mathbb A_\mu ^j$
is equal to
 $$ \begin{align*} \{[\chi_{1,n-j+1}^\vee],&[\chi_{1,n-j+3}^\vee+\chi_{2,n-j+2}^\vee],\ldots,\\ &[\chi_{1,n-1}^\vee+\chi_{2,n-2}^\vee+\cdots+\chi_{\frac{j}{2},n-\frac{j}{2}}^\vee],\ldots, [\chi_{j-2,n}^\vee+\chi_{j-1,n-1}^\vee],[\chi_{j,n}^\vee]\}. \end{align*} $$
$$ \begin{align*} \{[\chi_{1,n-j+1}^\vee],&[\chi_{1,n-j+3}^\vee+\chi_{2,n-j+2}^\vee],\ldots,\\ &[\chi_{1,n-1}^\vee+\chi_{2,n-2}^\vee+\cdots+\chi_{\frac{j}{2},n-\frac{j}{2}}^\vee],\ldots, [\chi_{j-2,n}^\vee+\chi_{j-1,n-1}^\vee],[\chi_{j,n}^\vee]\}. \end{align*} $$
Proof Let
![]() $(A,\varphi )$
be an extended semi-module for
$(A,\varphi )$
be an extended semi-module for
![]() $\mu $
. Let
$\mu $
. Let
![]() $\mu '$
be the type of A. If
$\mu '$
be the type of A. If
![]() $(A,\varphi )$
is noncyclic, then by Lemma 3.4,
$(A,\varphi )$
is noncyclic, then by Lemma 3.4,
![]() $\mu ^{\prime }_{\operatorname {\mathrm {dom}}}\prec \mu $
, i.e.,
$\mu ^{\prime }_{\operatorname {\mathrm {dom}}}\prec \mu $
, i.e.,
![]() $\mu ^{\prime }_{\operatorname {\mathrm {dom}}}=\omega _{n-1}$
. By Lemma 3.2, we have
$\mu ^{\prime }_{\operatorname {\mathrm {dom}}}=\omega _{n-1}$
. By Lemma 3.2, we have
![]() $A=\{0,1,\ldots ,n-1,\ldots \}$
. By Definition 3.3 (3),
$A=\{0,1,\ldots ,n-1,\ldots \}$
. By Definition 3.3 (3),
![]() $\varphi (a)=\max \{k\mid a+n-1-kn\in A\}$
for all
$\varphi (a)=\max \{k\mid a+n-1-kn\in A\}$
for all
![]() $a\in A$
. This contradicts to the assumption that
$a\in A$
. This contradicts to the assumption that
![]() $(A,\varphi )$
is noncyclic. Thus,
$(A,\varphi )$
is noncyclic. Thus,
![]() $(A,\varphi )$
is cyclic.
$(A,\varphi )$
is cyclic.
Since
![]() $\mu '$
satisfies
$\mu '$
satisfies
![]() $\nu _b\preceq w_{\max }\mu '$
, it is easy to check that
$\nu _b\preceq w_{\max }\mu '$
, it is easy to check that
for some
![]() $1\le k\le n-2$
and
$1\le k\le n-2$
and
![]() $k\le l\le n-2$
. Let
$k\le l\le n-2$
. Let
![]() $\bar A=\{a_0,a_1\ldots , a_{n-1}\}$
with
$\bar A=\{a_0,a_1\ldots , a_{n-1}\}$
with
![]() $a_0=\min \bar A$
. Then we have
$a_0=\min \bar A$
. Then we have
![]() $\varphi (a_0)=0,\varphi (a_{n-l-1})=0,\varphi (a_{n-k})=2$
and
$\varphi (a_0)=0,\varphi (a_{n-l-1})=0,\varphi (a_{n-k})=2$
and
![]() $\varphi (a_i)=1$
for
$\varphi (a_i)=1$
for
![]() $i\neq 0,n-l-1,n-k$
. Thus,
$i\neq 0,n-l-1,n-k$
. Thus,
 $$ \begin{align*} \mathcal V(A,\varphi)=&\{(a_{n-k},a_{n-l-1}+n),(a_{n-k},a_{n-l}),(a_{n-k},a_{n-l+1}),\ldots,(a_{n-k},a_{n-k-1})\}\\ \cup&\{(a_{n-k+1},a_{n-l-1}),(a_{n-k+2},a_{n-l-1}),\ldots, (a_{n-1},a_{n-l-1})\}, \end{align*} $$
$$ \begin{align*} \mathcal V(A,\varphi)=&\{(a_{n-k},a_{n-l-1}+n),(a_{n-k},a_{n-l}),(a_{n-k},a_{n-l+1}),\ldots,(a_{n-k},a_{n-k-1})\}\\ \cup&\{(a_{n-k+1},a_{n-l-1}),(a_{n-k+2},a_{n-l-1}),\ldots, (a_{n-1},a_{n-l-1})\}, \end{align*} $$
and
![]() $|\mathcal V(A,\varphi )|=l$
. Then by Proposition 3.7, the description of
$|\mathcal V(A,\varphi )|=l$
. Then by Proposition 3.7, the description of
![]() $\mathbb A_\mu ^l$
for each l in the lemma follows from direct computation.
$\mathbb A_\mu ^l$
for each l in the lemma follows from direct computation.
5.3 The semi-module stratification for
 $\omega _1+\omega _{n-3}$
$\omega _1+\omega _{n-3}$
Throughout this subsection, we set
![]() $\mu =\omega _1+\omega _{n-3}$
. Also we assume that
$\mu =\omega _1+\omega _{n-3}$
. Also we assume that
![]() $n\geq 7$
.
$n\geq 7$
.
Lemma 5.4 Every extended semi-module for
![]() $\mu $
is cyclic. For any
$\mu $
is cyclic. For any
![]() $1\le j\le \frac {3n-9}{2}(=\dim X_{\mu }(b))$
, we define
$1\le j\le \frac {3n-9}{2}(=\dim X_{\mu }(b))$
, we define
![]() $\mathbb A_\mu ^j$
similarly as in Section 3.3. Then
$\mathbb A_\mu ^j$
similarly as in Section 3.3. Then
![]() $|\mathbb A_\mu ^{\frac {3n-9}{2}}|=n-3$
and
$|\mathbb A_\mu ^{\frac {3n-9}{2}}|=n-3$
and
![]() $|\mathbb A_\mu ^{\frac {3n-11}{2}}|\le 2(n-4)$
.
$|\mathbb A_\mu ^{\frac {3n-11}{2}}|\le 2(n-4)$
.
Proof Using Lemma 5.1, we can show the first assertion similarly as the proof of Lemma 5.3. Indeed, for any semi-module
![]() $A^\lambda $
in Lemma 5.1, there exists a unique
$A^\lambda $
in Lemma 5.1, there exists a unique
![]() $\varphi $
such that
$\varphi $
such that
![]() $(A^\lambda ,\varphi )$
is an extended semi-module for some
$(A^\lambda ,\varphi )$
is an extended semi-module for some
![]() $\mu \in X_*(T)_+$
. The equality
$\mu \in X_*(T)_+$
. The equality
![]() $|\mathbb A_\mu ^{\frac {3n-9}{2}}|=n-3$
follows from the Chen-Zhu conjecture.
$|\mathbb A_\mu ^{\frac {3n-9}{2}}|=n-3$
follows from the Chen-Zhu conjecture.
Let
![]() $(A,\varphi )$
be an extended semi-module for
$(A,\varphi )$
be an extended semi-module for
![]() $\mu $
with type
$\mu $
with type
![]() $\mu '(\in W_0\mu )$
. Let
$\mu '(\in W_0\mu )$
. Let
![]() $0<k_1<k_2$
be integers such that
$0<k_1<k_2$
be integers such that
![]() $\mu '(1)=\mu '(k_1+1)=\mu '(k_2+1)=0$
, and let l be an integer such that
$\mu '(1)=\mu '(k_1+1)=\mu '(k_2+1)=0$
, and let l be an integer such that
![]() $\mu '(l+1)=2$
. Assume that
$\mu '(l+1)=2$
. Assume that
![]() $\nu _b\preceq w_{\max }s_{k_2+1}\mu '$
. Let
$\nu _b\preceq w_{\max }s_{k_2+1}\mu '$
. Let
![]() $(B,\psi )$
be an extended semi-module for
$(B,\psi )$
be an extended semi-module for
![]() $\mu $
with type
$\mu $
with type
![]() $s_{k_2+1}\mu '$
. Let
$s_{k_2+1}\mu '$
. Let
![]() $a_0=\min \bar A$
(resp.
$a_0=\min \bar A$
(resp.
![]() $b_0=\min \bar B$
) and let inductively
$b_0=\min \bar B$
) and let inductively
![]() $a_i=a_{i-1}+n-2-\mu '(i)n$
(resp.
$a_i=a_{i-1}+n-2-\mu '(i)n$
(resp.
![]() $b_i=b_{i-1}+n-2-(s_{k_2+1}\mu ')(i)n$
) for
$b_i=b_{i-1}+n-2-(s_{k_2+1}\mu ')(i)n$
) for
![]() $i=1,\ldots , n$
. Then
$i=1,\ldots , n$
. Then
![]() $a_0=a_n$
(resp.
$a_0=a_n$
(resp.
![]() $b_0=b_n$
) and
$b_0=b_n$
) and
![]() $\{a_0,a_1,\ldots ,a_{n-1}\}=\bar A$
(resp.
$\{a_0,a_1,\ldots ,a_{n-1}\}=\bar A$
(resp.
![]() $\{b_0,b_1,\ldots ,b_{n-1}\}=\bar B$
). We will show that if
$\{b_0,b_1,\ldots ,b_{n-1}\}=\bar B$
). We will show that if
![]() $l>k_2+1$
(resp.
$l>k_2+1$
(resp.
![]() $l=k_2+1$
), then
$l=k_2+1$
), then
![]() $|\mathcal V(B,\psi )|\le |\mathcal V(A,\varphi )|$
(resp.
$|\mathcal V(B,\psi )|\le |\mathcal V(A,\varphi )|$
(resp.
![]() $|\mathcal V(B,\psi )|<|\mathcal V(A,\varphi )|-1$
). Moreover, the equality does not hold if
$|\mathcal V(B,\psi )|<|\mathcal V(A,\varphi )|-1$
). Moreover, the equality does not hold if
![]() $k_2-k_1\le 3.$
$k_2-k_1\le 3.$
Note that we have
![]() $\varphi (a_{0})=\varphi (a_{k_1})=\varphi (a_{k_2})=0,\varphi (a_l)=2,\psi (b_0)=\psi (b_{k_1})=\psi (b_{k_2+1})=0,\psi (b_l)=2$
. Note also that
$\varphi (a_{0})=\varphi (a_{k_1})=\varphi (a_{k_2})=0,\varphi (a_l)=2,\psi (b_0)=\psi (b_{k_1})=\psi (b_{k_2+1})=0,\psi (b_l)=2$
. Note also that
 $$ \begin{align*} \mathcal V(A,\varphi)=&\{(a,a')\mid a\in \bar A \text{with} \varphi(a)=1, a'=a_{k_1} \text{or} a_{k_2}\}\\ \sqcup &\{(a_l,a')\mid a_l<a',\varphi(a')<2\}, \end{align*} $$
$$ \begin{align*} \mathcal V(A,\varphi)=&\{(a,a')\mid a\in \bar A \text{with} \varphi(a)=1, a'=a_{k_1} \text{or} a_{k_2}\}\\ \sqcup &\{(a_l,a')\mid a_l<a',\varphi(a')<2\}, \end{align*} $$
and
 $$ \begin{align*} \mathcal V(B,\psi)=&\{(b,b')\mid b\in \bar B \text{with} \psi(b)=1, b'=b_{k_1} \text{or} b_{k_2+1}\}\\ \sqcup &\{(b_l,b')\mid b_l<b',\psi(b')<2\}. \end{align*} $$
$$ \begin{align*} \mathcal V(B,\psi)=&\{(b,b')\mid b\in \bar B \text{with} \psi(b)=1, b'=b_{k_1} \text{or} b_{k_2+1}\}\\ \sqcup &\{(b_l,b')\mid b_l<b',\psi(b')<2\}. \end{align*} $$
Let
![]() $\mathcal V(A,\varphi )_1$
(resp.
$\mathcal V(A,\varphi )_1$
(resp.
![]() $\mathcal V(B,\psi )_1$
) be the first subset in
$\mathcal V(B,\psi )_1$
) be the first subset in
![]() $\mathcal V(A,\varphi )$
(resp.
$\mathcal V(A,\varphi )$
(resp.
![]() $\mathcal V(B,\psi )$
) above, and let
$\mathcal V(B,\psi )$
) above, and let
![]() $\mathcal V(A,\varphi )_2$
(resp.
$\mathcal V(A,\varphi )_2$
(resp.
![]() $\mathcal V(B,\psi )_2$
) be its complement.
$\mathcal V(B,\psi )_2$
) be its complement.
If
![]() $l>k_2+1$
, then it follows that
$l>k_2+1$
, then it follows that
 $$ \begin{align*}b_k=\begin{cases} a_k+1 & (k\neq k_2+1)\\ a_k+1-n & (k=k_2+1) \end{cases},\quad \psi(b_k)=\begin{cases} \varphi(a_k) & (k\neq k_2,k_2+1)\\ 1-\varphi(a_k) & (k=k_2,k_2+1). \end{cases}\end{align*} $$
$$ \begin{align*}b_k=\begin{cases} a_k+1 & (k\neq k_2+1)\\ a_k+1-n & (k=k_2+1) \end{cases},\quad \psi(b_k)=\begin{cases} \varphi(a_k) & (k\neq k_2,k_2+1)\\ 1-\varphi(a_k) & (k=k_2,k_2+1). \end{cases}\end{align*} $$
In particular,
![]() $b_{k_2+1}-1=a_{k_2}-2$
. So
$b_{k_2+1}-1=a_{k_2}-2$
. So
![]() $|\mathcal V(B,\psi )_1|>|\mathcal V(A,\varphi )_1|$
implies that
$|\mathcal V(B,\psi )_1|>|\mathcal V(A,\varphi )_1|$
implies that
![]() $|\mathcal V(B,\psi )_1|=|\mathcal V(A,\varphi )_1|+1$
and
$|\mathcal V(B,\psi )_1|=|\mathcal V(A,\varphi )_1|+1$
and
![]() $b_{k_2}<b_{k_1}$
. By the fact
$b_{k_2}<b_{k_1}$
. By the fact
![]() $(a_l, a_{k_2+1})\in \mathcal V(A,\varphi )_2$
, we always have
$(a_l, a_{k_2+1})\in \mathcal V(A,\varphi )_2$
, we always have
![]() $|\mathcal V(B,\psi )_2|< |\mathcal V(A,\varphi )_2|$
. Thus,
$|\mathcal V(B,\psi )_2|< |\mathcal V(A,\varphi )_2|$
. Thus,
![]() $|\mathcal V(B,\psi )|\le |\mathcal V(A,\varphi )|$
. Moreover, if
$|\mathcal V(B,\psi )|\le |\mathcal V(A,\varphi )|$
. Moreover, if
![]() $k_2-k_1\le 3$
, then the equality does not hold because
$k_2-k_1\le 3$
, then the equality does not hold because
![]() $b_{k_2}\geq b_{k_1}$
.
$b_{k_2}\geq b_{k_1}$
.
If
![]() $l=k_2+1$
, then it follows that
$l=k_2+1$
, then it follows that
 $$ \begin{align*}b_k=\begin{cases} a_k+2 & (k\neq k_2+1)\\ a_k+2-2n & (k=k_2+1) \end{cases},\quad \psi(b_k)=\begin{cases} \varphi(a_k) & (k\neq k_2,k_2+1)\\ 2-\varphi(a_k) & (k=k_2,k_2+1). \end{cases}\end{align*} $$
$$ \begin{align*}b_k=\begin{cases} a_k+2 & (k\neq k_2+1)\\ a_k+2-2n & (k=k_2+1) \end{cases},\quad \psi(b_k)=\begin{cases} \varphi(a_k) & (k\neq k_2,k_2+1)\\ 2-\varphi(a_k) & (k=k_2,k_2+1). \end{cases}\end{align*} $$
In particular,
![]() $b_{k_2+1}-2=a_{k_2}-2-n$
. By
$b_{k_2+1}-2=a_{k_2}-2-n$
. By
![]() $\nu _b\preceq w_{\max }s_{k_2+1}\mu '$
, we have
$\nu _b\preceq w_{\max }s_{k_2+1}\mu '$
, we have
![]() $k_2\le \frac {n-3}{2}$
. Using this, we can easily check that
$k_2\le \frac {n-3}{2}$
. Using this, we can easily check that
![]() $|\mathcal V(B,\psi )|<|\mathcal V(A,\varphi )_1|$
and
$|\mathcal V(B,\psi )|<|\mathcal V(A,\varphi )_1|$
and
![]() $\mathcal V(A,\varphi )_2=\{(a_{k_2+1},a_{k_2}+n)\}$
. Thus,
$\mathcal V(A,\varphi )_2=\{(a_{k_2+1},a_{k_2}+n)\}$
. Thus,
![]() $|\mathcal V(B,\psi )|<|\mathcal V(A,\varphi )|-1$
.
$|\mathcal V(B,\psi )|<|\mathcal V(A,\varphi )|-1$
.
Assume that
![]() $\nu _b\preceq w_{\max }s_{k_1+1}\mu '$
. Let
$\nu _b\preceq w_{\max }s_{k_1+1}\mu '$
. Let
![]() $(C,\chi )$
be an extended semi-module for
$(C,\chi )$
be an extended semi-module for
![]() $\mu $
with type
$\mu $
with type
![]() $s_{k_1+1}\mu '$
. Similarly as above, we can show that if
$s_{k_1+1}\mu '$
. Similarly as above, we can show that if
![]() $l\geq k_1+1$
, then
$l\geq k_1+1$
, then
![]() $|\mathcal V(C,\chi )|\le |\mathcal V(A,\varphi )|$
. Therefore,
$|\mathcal V(C,\chi )|\le |\mathcal V(A,\varphi )|$
. Therefore,
![]() $|\mathcal V(A,\varphi )|\geq \frac {3n-11}{2}$
holds only if
$|\mathcal V(A,\varphi )|\geq \frac {3n-11}{2}$
holds only if
![]() $k_2=2$
or
$k_2=2$
or
![]() $l>k_2=3$
. From this and
$l>k_2=3$
. From this and
![]() $|\mathbb A_\mu ^{\frac {3n-9}{2}}|=n-3$
, we obtain
$|\mathbb A_\mu ^{\frac {3n-9}{2}}|=n-3$
, we obtain
![]() $|\mathbb A_\mu ^{\frac {3n-11}{2}}|\le 2(n-4)$
.
$|\mathbb A_\mu ^{\frac {3n-11}{2}}|\le 2(n-4)$
.
5.4 The semi-module stratification for
 $\omega _1+\omega _2,\omega _4+\omega _{n-1}$
$\omega _1+\omega _2,\omega _4+\omega _{n-1}$
Lemma 5.5 Assume that
![]() $n=5$
. Set
$n=5$
. Set
![]() $\mu =\omega _1+\omega _2$
. Then every extended semi-module for
$\mu =\omega _1+\omega _2$
. Then every extended semi-module for
![]() $\mu $
is cyclic. For any
$\mu $
is cyclic. For any
![]() $1\le j\le 3(=\dim X_{\mu }(b))$
, we define
$1\le j\le 3(=\dim X_{\mu }(b))$
, we define
![]() $\mathbb A_\mu ^j$
similarly as in Section 3.3. Then
$\mathbb A_\mu ^j$
similarly as in Section 3.3. Then
Proof The first assertion follows similarly as the proof of Lemma 5.3. The second assertion follows from direct computation.
Lemma 5.6 Assume that
![]() $n=7$
or
$n=7$
or
![]() $8$
. Let
$8$
. Let
![]() $\mu $
be
$\mu $
be
![]() $\omega _1+\omega _2$
or
$\omega _1+\omega _2$
or
![]() $\omega _4+\omega _{n-1}$
. Then there exists a noncyclic extended semi-module for
$\omega _4+\omega _{n-1}$
. Then there exists a noncyclic extended semi-module for
![]() $\mu $
.
$\mu $
.
Proof As described in Lemma 5.2, there exists a unique top cyclic extended semi-module
![]() $(A^\lambda ,\varphi )$
for
$(A^\lambda ,\varphi )$
for
![]() $\omega _3$
. We define
$\omega _3$
. We define
![]() $\varphi '\colon \mathbb Z\rightarrow \mathbb N\cup \{-\infty \}$
by setting
$\varphi '\colon \mathbb Z\rightarrow \mathbb N\cup \{-\infty \}$
by setting
 $$ \begin{align*}\varphi'(a)= \begin{cases} \varphi(a) & (a\neq 1)\\ 0 & (a=1). \end{cases}\end{align*} $$
$$ \begin{align*}\varphi'(a)= \begin{cases} \varphi(a) & (a\neq 1)\\ 0 & (a=1). \end{cases}\end{align*} $$
Then it is straightforward to check that
![]() $(A^\lambda ,\varphi ')$
is a noncyclic extended semi-module for
$(A^\lambda ,\varphi ')$
is a noncyclic extended semi-module for
![]() $\omega _1+\omega _2$
. The proof for
$\omega _1+\omega _2$
. The proof for
![]() $\omega _4+\omega _{n-1}$
is similar.
$\omega _4+\omega _{n-1}$
is similar.
6 The Ekedahl–Oort stratification
Keep the notations and assumptions in Section 3. For
![]() $\mu \in X_*(T)_+$
, set
$\mu \in X_*(T)_+$
, set
By Theorem 2.9,
![]() $X_w(b)\neq \emptyset $
if
$X_w(b)\neq \emptyset $
if
![]() $w\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}$
.
$w\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}$
.
6.1 The Ekedahl–Oort stratification for
 $\omega _i$
$\omega _i$
Throughout this subsection, we set
![]() $\mu =\omega _i$
and
$\mu =\omega _i$
and
![]() $c=s_is_{i+1}\cdots s_{n-1}s_{i-1}\cdots s_2s_1$
. By [Reference He, Nie and Yu23, Theorem 2.7], we have
$c=s_is_{i+1}\cdots s_{n-1}s_{i-1}\cdots s_2s_1$
. By [Reference He, Nie and Yu23, Theorem 2.7], we have
![]() $\dim X_{\varpi ^\mu c}(b)=\dim X_\mu (b)=\langle \mu ,\rho \rangle -\frac {n-1}{2}$
.
$\dim X_{\varpi ^\mu c}(b)=\dim X_\mu (b)=\langle \mu ,\rho \rangle -\frac {n-1}{2}$
.
Note that
![]() $|W_{\operatorname {\mathrm {supp}}_\sigma (w)}|$
is finite if and only if
$|W_{\operatorname {\mathrm {supp}}_\sigma (w)}|$
is finite if and only if
![]() $\operatorname {\mathrm {supp}}_\sigma (w)\neq \tilde S$
. Since
$\operatorname {\mathrm {supp}}_\sigma (w)\neq \tilde S$
. Since
![]() $\tau ^m$
acts transitively on
$\tau ^m$
acts transitively on
![]() $\tilde S$
,
$\tilde S$
,
![]() $\operatorname {\mathrm {supp}}_\sigma (w)\neq \tilde S$
if and only if
$\operatorname {\mathrm {supp}}_\sigma (w)\neq \tilde S$
if and only if
![]() $w\in \Omega $
.
$w\in \Omega $
.
Lemma 6.1 Assume that
![]() $n\geq 9$
and
$n\geq 9$
and
![]() $4\le i\le n-4$
. Set
$4\le i\le n-4$
. Set
![]() $y=cs_is_{i+1}s_{i-1}=(1\ i+1\ i+3\ i+4\ \cdots \ n\ i\ i-2\ \cdots \ 3\ 2)(i-1\ i+2)$
. Then we have
$y=cs_is_{i+1}s_{i-1}=(1\ i+1\ i+3\ i+4\ \cdots \ n\ i\ i-2\ \cdots \ 3\ 2)(i-1\ i+2)$
. Then we have
![]() $\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )$
and
$\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )$
and
![]() $X_{\varpi ^\mu y}(b)\neq \emptyset $
.
$X_{\varpi ^\mu y}(b)\neq \emptyset $
.
Proof Under the assumption in the lemma, we have
![]() $\ell (\varpi ^\mu y)=\langle \mu , 2\rho \rangle -\ell (y)(>0)$
and hence
$\ell (\varpi ^\mu y)=\langle \mu , 2\rho \rangle -\ell (y)(>0)$
and hence
![]() $\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )$
(cf. [Reference Macdonald31, (2.4.5)]). So, by Lemma 2.8 and Theorem 2.9,
$\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )$
(cf. [Reference Macdonald31, (2.4.5)]). So, by Lemma 2.8 and Theorem 2.9,
![]() $X_{\varpi ^\mu y}(b)\neq \emptyset $
is equivalent to saying
$X_{\varpi ^\mu y}(b)\neq \emptyset $
is equivalent to saying
![]() $\operatorname {\mathrm {supp}}(ryr^{-1})\subsetneq S$
for any
$\operatorname {\mathrm {supp}}(ryr^{-1})\subsetneq S$
for any
![]() $r\in W_0$
such that
$r\in W_0$
such that
![]() $r(\Phi _+\setminus \Phi _{\varpi ^\mu y})\subset \Phi _+$
. It is easy to check that
$r(\Phi _+\setminus \Phi _{\varpi ^\mu y})\subset \Phi _+$
. It is easy to check that
In particular, we have
![]() $\chi _{1,i+2},\chi _{i-1,n}\in \Phi _+\setminus \Phi _{\varpi ^\mu y}$
. Note that we can decompose
$\chi _{1,i+2},\chi _{i-1,n}\in \Phi _+\setminus \Phi _{\varpi ^\mu y}$
. Note that we can decompose
![]() $ryr^{-1}$
into disjoint cycles as
$ryr^{-1}$
into disjoint cycles as
for any
![]() $r\in W_0$
. So if
$r\in W_0$
. So if
![]() $ryr^{-1}\in \bigcup _{J\subsetneq S}W_J$
, then
$ryr^{-1}\in \bigcup _{J\subsetneq S}W_J$
, then
![]() $(r(i-1)\ r(i+2))=(1\ 2)$
or
$(r(i-1)\ r(i+2))=(1\ 2)$
or
![]() $(n-1\ n)$
. This implies that
$(n-1\ n)$
. This implies that
![]() $r\chi _{1,i+2}$
or
$r\chi _{1,i+2}$
or
![]() $r\chi _{i-1,n}$
is negative and hence that r does not satisfy
$r\chi _{i-1,n}$
is negative and hence that r does not satisfy
![]() $r(\Phi _+\setminus \Phi _{\varpi ^\mu y})\subset \Phi _+$
. Thus, we have
$r(\Phi _+\setminus \Phi _{\varpi ^\mu y})\subset \Phi _+$
. Thus, we have
![]() $X_{\varpi ^\mu y}(b)\neq \emptyset $
.
$X_{\varpi ^\mu y}(b)\neq \emptyset $
.
Lemma 6.2 Assume that
![]() $n\geq 9$
and
$n\geq 9$
and
![]() $i=3$
(resp.
$i=3$
(resp.
![]() $i=n-3$
). Set
$i=n-3$
). Set
![]() $y=cs_3s_4s_5s_6s_2$
(resp.
$y=cs_3s_4s_5s_6s_2$
(resp.
![]() $y=cs_{n-3}s_{n-4}s_{n-5}s_{n-6}s_{n-2}$
). Then we have
$y=cs_{n-3}s_{n-4}s_{n-5}s_{n-6}s_{n-2}$
). Then we have
![]() $\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )$
and
$\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )$
and
![]() $X_{\varpi ^\mu y}(b)\neq \emptyset $
.
$X_{\varpi ^\mu y}(b)\neq \emptyset $
.
Proof We only treat the case
![]() $i=3$
. The proof for the case
$i=3$
. The proof for the case
![]() $i=n-3$
is similar.
$i=n-3$
is similar.
The first assertion is easy. To show the second assertion, by Lemma 2.8 and Theorem 2.9, it suffices to check that
![]() $ryr^{-1}\notin \bigcup _{J\subsetneq S}W_J$
for any
$ryr^{-1}\notin \bigcup _{J\subsetneq S}W_J$
for any
![]() $r\in W_0$
such that
$r\in W_0$
such that
![]() $r(\Phi _+\setminus \Phi _{\varpi ^\mu y})\subset \Phi _+$
. By an explicit calculation, it follows that
$r(\Phi _+\setminus \Phi _{\varpi ^\mu y})\subset \Phi _+$
. By an explicit calculation, it follows that
![]() $\chi _{1,7},\chi _{2,9}\in \Phi _+\setminus \Phi _{\varpi ^\mu y}$
and
$\chi _{1,7},\chi _{2,9}\in \Phi _+\setminus \Phi _{\varpi ^\mu y}$
and
If
![]() $ryr^{-1}\in \bigcup _{J\subsetneq S}W_J$
, then
$ryr^{-1}\in \bigcup _{J\subsetneq S}W_J$
, then
![]() $(r(2)\ r(5)\ r(7))$
is equal to
$(r(2)\ r(5)\ r(7))$
is equal to
![]() $(1\ 2\ 3)$
or
$(1\ 2\ 3)$
or
![]() $(n-2\ n-1\ n)$
. This implies that r does not satisfy
$(n-2\ n-1\ n)$
. This implies that r does not satisfy
![]() $r(\Phi _+\setminus \Phi _{\varpi ^\mu y})\subset \Phi _+$
. Thus, we have
$r(\Phi _+\setminus \Phi _{\varpi ^\mu y})\subset \Phi _+$
. Thus, we have
![]() $X_{\varpi ^\mu y}(b)\neq \emptyset $
.
$X_{\varpi ^\mu y}(b)\neq \emptyset $
.
Lemma 6.3 Assume that
![]() $n\geq 9$
and
$n\geq 9$
and
![]() $i=3$
(resp.
$i=3$
(resp.
![]() $i=n-3$
). Let y be
$i=n-3$
). Let y be
![]() $cs_is_{i-1}$
or
$cs_is_{i-1}$
or
![]() $cs_is_{i+1}$
. Then we have
$cs_is_{i+1}$
. Then we have
![]() $\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )$
and
$\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )$
and
![]() $X_{\varpi ^\mu y}(b)\neq \emptyset $
.
$X_{\varpi ^\mu y}(b)\neq \emptyset $
.
Proof The proof is similar to the proof of Lemmas 6.1 and 6.2. Note that y is a n-cycle in this case.
Proposition 6.4 Assume that
![]() $n\geq 9$
and
$n\geq 9$
and
![]() $3\le i\le n-3$
. Then the semi-module stratification of
$3\le i\le n-3$
. Then the semi-module stratification of
![]() $X_\mu (b)$
is not a refinement of the Ekedahl–Oort stratification.
$X_\mu (b)$
is not a refinement of the Ekedahl–Oort stratification.
Proof First assume that
![]() $n\geq 9$
and
$n\geq 9$
and
![]() $4\le i\le n-4$
. Let
$4\le i\le n-4$
. Let
![]() $\varpi ^\mu y\in {^S\tilde W}$
be as in Lemma 6.1. Let
$\varpi ^\mu y\in {^S\tilde W}$
be as in Lemma 6.1. Let
![]() $\mathcal T$
be a reduction tree of
$\mathcal T$
be a reduction tree of
![]() $\varpi ^\mu y$
. By Proposition 2.6, we have
$\varpi ^\mu y$
. By Proposition 2.6, we have
where
![]() $\underline p$
runs over all the reduction paths in
$\underline p$
runs over all the reduction paths in
![]() $\mathcal T$
with
$\mathcal T$
with
![]() $\operatorname {\mathrm {end}}(\underline p)=\tau ^m$
. Set
$\operatorname {\mathrm {end}}(\underline p)=\tau ^m$
. Set
![]() $d=\dim X_\mu (b)=\langle \mu ,\rho \rangle -\frac {n-1}{2}$
. Suppose that the semi-module stratification of
$d=\dim X_\mu (b)=\langle \mu ,\rho \rangle -\frac {n-1}{2}$
. Suppose that the semi-module stratification of
![]() $X_\mu (b)$
is a refinement of the Ekedahl–Oort stratification. Note that
$X_\mu (b)$
is a refinement of the Ekedahl–Oort stratification. Note that
![]() $Z(\varpi ^\mu c)=Z(\varpi ^\mu y)=\{1\}$
. By Lemma 2.1, Proposition 2.3 and
$Z(\varpi ^\mu c)=Z(\varpi ^\mu y)=\{1\}$
. By Lemma 2.1, Proposition 2.3 and
![]() $\dim X_{\varpi ^\mu c}(b)=d$
, we have
$\dim X_{\varpi ^\mu c}(b)=d$
, we have
![]() $\ell _I(\underline p)+\ell _{II}(\underline p)\le \dim X_{\varpi ^\mu y}(b)\le d-1$
for any
$\ell _I(\underline p)+\ell _{II}(\underline p)\le \dim X_{\varpi ^\mu y}(b)\le d-1$
for any
![]() $\underline p$
. On the other hand, we have
$\underline p$
. On the other hand, we have
![]() $\ell _I(\underline p)+2\ell _{II}(\underline p)=\ell (\varpi ^\mu y)=2d-3$
. Thus, we have
$\ell _I(\underline p)+2\ell _{II}(\underline p)=\ell (\varpi ^\mu y)=2d-3$
. Thus, we have
![]() $\ell _I(\underline p)+\ell _{II}(\underline p)=d-1$
and
$\ell _I(\underline p)+\ell _{II}(\underline p)=d-1$
and
![]() $\ell _I(\underline p)=1$
for any
$\ell _I(\underline p)=1$
for any
![]() $\underline p$
. It follows that
$\underline p$
. It follows that
where
![]() $k\geq 1$
is the number of irreducible components of
$k\geq 1$
is the number of irreducible components of
![]() $X_{\varpi ^\mu y}(b)^0$
. Again by Lemma 2.1 and the fact that each
$X_{\varpi ^\mu y}(b)^0$
. Again by Lemma 2.1 and the fact that each
![]() $S_{A,\varphi }$
is locally closed, we have
$S_{A,\varphi }$
is locally closed, we have
![]() $|\{(A,\varphi )\mid \dim S_{A,\varphi }=d-1, S_{A,\varphi }\subseteq \pi (X_{\varpi ^\mu y}(b)^0)\}|=k$
. By Lemma 3.4, it follows that
$|\{(A,\varphi )\mid \dim S_{A,\varphi }=d-1, S_{A,\varphi }\subseteq \pi (X_{\varpi ^\mu y}(b)^0)\}|=k$
. By Lemma 3.4, it follows that
![]() $|\pi (X_{\varpi ^\mu y}(b)^{0})^\sigma |\geq kq^{d-1}$
, which is a contradiction. This implies the proposition in this case.
$|\pi (X_{\varpi ^\mu y}(b)^{0})^\sigma |\geq kq^{d-1}$
, which is a contradiction. This implies the proposition in this case.
Next assume that
![]() $n\geq 10$
and
$n\geq 10$
and
![]() $i=3, n-3$
. Let
$i=3, n-3$
. Let
![]() $\varpi ^\mu y\in {^S\tilde W}$
be as in Lemma 6.2. Suppose that the semi-module stratification of
$\varpi ^\mu y\in {^S\tilde W}$
be as in Lemma 6.2. Suppose that the semi-module stratification of
![]() $X_\mu (b)$
is a refinement of the Ekedahl–Oort stratification. Similarly as above, we can check that
$X_\mu (b)$
is a refinement of the Ekedahl–Oort stratification. Similarly as above, we can check that
Note that
![]() $Z(\varpi ^\mu c)=Z(\varpi ^\mu cs_is_{i-1})=Z(\varpi ^\mu cs_is_{i+1})=Z(\varpi ^\mu y)=\{1\}$
. By Lemma 2.1 and Proposition 3.13, we have
$Z(\varpi ^\mu c)=Z(\varpi ^\mu cs_is_{i-1})=Z(\varpi ^\mu cs_is_{i+1})=Z(\varpi ^\mu y)=\{1\}$
. By Lemma 2.1 and Proposition 3.13, we have
![]() $\dim X_{\varpi ^\mu y}(b)\le d-2$
. Similarly as above, it follows that
$\dim X_{\varpi ^\mu y}(b)\le d-2$
. Similarly as above, it follows that
![]() $|\pi (X_{\varpi ^\mu y}(b)^{0})^\sigma |=k(q-1)q^{d-3}$
and
$|\pi (X_{\varpi ^\mu y}(b)^{0})^\sigma |=k(q-1)q^{d-3}$
and
![]() $|\pi (X_{\varpi ^\mu y}(b)^{0})^\sigma |\geq kq^{d-2}$
. This is a contradiction, which finishes the proof.
$|\pi (X_{\varpi ^\mu y}(b)^{0})^\sigma |\geq kq^{d-2}$
. This is a contradiction, which finishes the proof.
The following proposition is the complement of Proposition 6.4.
Proposition 6.5 We have
 $$ \begin{align*} {^S\mathrm{Adm}}(\omega_1)_{\operatorname{\mathrm{cyc}}}&=\{\tau\},\\ {^S\mathrm{Adm}}(\omega_2)_{\operatorname{\mathrm{cyc}}}&=\{\tau^2, s_0s_{n-1}\tau^2,s_0s_{n-1}s_{n-2}s_{n-3}\tau^2,\ldots, s_0s_{n-1}\cdots s_5s_4\tau^2\} &(n\geq 5),\\ {^S\mathrm{Adm}}(\omega_3)_{\operatorname{\mathrm{cyc}}}&=\{\tau^3,s_0s_6\tau^3,s_0s_6s_1s_0\tau^3,s_0s_6s_5s_1\tau^3,s_0s_6s_5s_1s_0s_6\tau^3\} &(n=7),\\ {^S\mathrm{Adm}}(\omega_3)_{\operatorname{\mathrm{cyc}}}&=\{\tau^3,s_0s_1\tau^3,s_0s_7s_6s_5\tau^3,s_0s_7s_6s_1\tau^3,s_0s_7s_6s_5s_1s_0\tau^3,\\ &\hspace{3.54cm}s_0s_7s_6s_1s_0s_7\tau^3,s_0s_7s_6s_5s_1s_0s_7s_6\tau^3\} &(n=8). \end{align*} $$
$$ \begin{align*} {^S\mathrm{Adm}}(\omega_1)_{\operatorname{\mathrm{cyc}}}&=\{\tau\},\\ {^S\mathrm{Adm}}(\omega_2)_{\operatorname{\mathrm{cyc}}}&=\{\tau^2, s_0s_{n-1}\tau^2,s_0s_{n-1}s_{n-2}s_{n-3}\tau^2,\ldots, s_0s_{n-1}\cdots s_5s_4\tau^2\} &(n\geq 5),\\ {^S\mathrm{Adm}}(\omega_3)_{\operatorname{\mathrm{cyc}}}&=\{\tau^3,s_0s_6\tau^3,s_0s_6s_1s_0\tau^3,s_0s_6s_5s_1\tau^3,s_0s_6s_5s_1s_0s_6\tau^3\} &(n=7),\\ {^S\mathrm{Adm}}(\omega_3)_{\operatorname{\mathrm{cyc}}}&=\{\tau^3,s_0s_1\tau^3,s_0s_7s_6s_5\tau^3,s_0s_7s_6s_1\tau^3,s_0s_7s_6s_5s_1s_0\tau^3,\\ &\hspace{3.54cm}s_0s_7s_6s_1s_0s_7\tau^3,s_0s_7s_6s_5s_1s_0s_7s_6\tau^3\} &(n=8). \end{align*} $$
Let
![]() $\varpi ^\mu y\in {^S\tilde W}$
be one of the elements above. Then there exists
$\varpi ^\mu y\in {^S\tilde W}$
be one of the elements above. Then there exists
![]() $v\in \operatorname {\mathrm {LP}}(\varpi ^\mu y)$
such that
$v\in \operatorname {\mathrm {LP}}(\varpi ^\mu y)$
such that
![]() $v^{-1}yv$
is a Coxeter element. Moreover,
$v^{-1}yv$
is a Coxeter element. Moreover,
![]() $X_w(b)=\emptyset $
for any
$X_w(b)=\emptyset $
for any
![]() $w\in {^S\mathrm {Adm}}(\mu )\setminus {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}$
, and the semi-module stratification of
$w\in {^S\mathrm {Adm}}(\mu )\setminus {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}$
, and the semi-module stratification of
![]() $X_{\mu }(b)$
is a refinement of the Ekedahl–Oort stratification.
$X_{\mu }(b)$
is a refinement of the Ekedahl–Oort stratification.
Proof The equalities in the proposition follow from easy calculations. For other statements, we only prove the case for
![]() $\omega _2$
. Other cases can be checked similarly.
$\omega _2$
. Other cases can be checked similarly.
Set
![]() $d=\frac {n-3}{2}$
. For
$d=\frac {n-3}{2}$
. For
![]() $0\le j\le d$
, we set
$0\le j\le d$
, we set
![]() $w_j=s_0s_{n-1}\cdots s_{n-2j+1}\tau ^2$
. Then
$w_j=s_0s_{n-1}\cdots s_{n-2j+1}\tau ^2$
. Then
![]() $\ell (w_j)=2j$
and
$\ell (w_j)=2j$
and
Also it is easy to check that
Clearly there exists
![]() $r\in W_0$
with
$r\in W_0$
with
![]() $r(\Phi _+\setminus \Phi _{w_j})\subset \Phi _+$
such that
$r(\Phi _+\setminus \Phi _{w_j})\subset \Phi _+$
such that
![]() $rp(w_j)r^{-1}$
is a Coxeter element (cf. [Reference Shimada40, Lemma 5.1]).
$rp(w_j)r^{-1}$
is a Coxeter element (cf. [Reference Shimada40, Lemma 5.1]).
For an integer j, let
![]() $0\le [j]<n$
denote its residue modulo n. For
$0\le [j]<n$
denote its residue modulo n. For
![]() $a,b\in \mathbb N$
with
$a,b\in \mathbb N$
with
![]() $a-b\in 2\mathbb Z$
, we define
$a-b\in 2\mathbb Z$
, we define
![]() $t_{a,b}=s_{[b-2]}\cdots s_{[a+2]}s_{[a]}$
. Set
$t_{a,b}=s_{[b-2]}\cdots s_{[a+2]}s_{[a]}$
. Set
 $$ \begin{align*} w_{j,0}=w_j,w_{j,1}=t_{0,n-2j+1}w_jt_{0,n-2j+1}^{-1}, w_{j,2}=t_{n-1,n-2j+2}w_{j,1}t_{n-1,n-2j+2}^{-1},\\ \ldots, w_{j,j}=t_{n-j+1,n-j}w_{j,j-1}t_{n-j+1,n-j}^{-1}. \end{align*} $$
$$ \begin{align*} w_{j,0}=w_j,w_{j,1}=t_{0,n-2j+1}w_jt_{0,n-2j+1}^{-1}, w_{j,2}=t_{n-1,n-2j+2}w_{j,1}t_{n-1,n-2j+2}^{-1},\\ \ldots, w_{j,j}=t_{n-j+1,n-j}w_{j,j-1}t_{n-j+1,n-j}^{-1}. \end{align*} $$
It is easy to check that the simple reflections in
![]() $t_{0,n-2j+1},t_{n-1,n-2j+2},\ldots ,t_{n-j+1,n-j}$
define
$t_{0,n-2j+1},t_{n-1,n-2j+2},\ldots ,t_{n-j+1,n-j}$
define
 $$ \begin{align*} w_j=w_{j,0}\rightarrow_{\sigma}w_{j,1}=s_{n-1}s_{n-2}\cdots s_{n-2j+2}\tau^2&\rightarrow_{\sigma}w_{j,2}=s_{n-2}s_{n-3}\cdots s_{n-2j+3}\tau^2\\ &\rightarrow_{\sigma}\cdots \rightarrow_{\sigma} w_{j,j}=\tau^2. \end{align*} $$
$$ \begin{align*} w_j=w_{j,0}\rightarrow_{\sigma}w_{j,1}=s_{n-1}s_{n-2}\cdots s_{n-2j+2}\tau^2&\rightarrow_{\sigma}w_{j,2}=s_{n-2}s_{n-3}\cdots s_{n-2j+3}\tau^2\\ &\rightarrow_{\sigma}\cdots \rightarrow_{\sigma} w_{j,j}=\tau^2. \end{align*} $$
Let
![]() $\underline p_j$
be the reduction path (in a suitable reduction tree) defined by this reduction. Using Lemma 2.1, Propositions 2.5, 2.6 and 3.13, we can check that
$\underline p_j$
be the reduction path (in a suitable reduction tree) defined by this reduction. Using Lemma 2.1, Propositions 2.5, 2.6 and 3.13, we can check that
![]() $X_{w_j}(\tau ^2)=X_{\underline p_j}$
and
$X_{w_j}(\tau ^2)=X_{\underline p_j}$
and
![]() $X_w(\tau ^2)=\emptyset $
for any
$X_w(\tau ^2)=\emptyset $
for any
![]() $w\in {^S\mathrm {Adm}}(\omega _2)\setminus {^S\mathrm {Adm}}(\omega _2)_{\operatorname {\mathrm {cyc}}}$
by counting the number of rational points of
$w\in {^S\mathrm {Adm}}(\omega _2)\setminus {^S\mathrm {Adm}}(\omega _2)_{\operatorname {\mathrm {cyc}}}$
by counting the number of rational points of
![]() $X_\mu (\tau ^2)^0$
(note that
$X_\mu (\tau ^2)^0$
(note that
![]() $X_{\tau ^2}(\tau ^2)^0=\{I\}$
). It is easy to check that
$X_{\tau ^2}(\tau ^2)^0=\{I\}$
). It is easy to check that
 $$ \begin{align*}\ell(t_{n-j+1,n-j}\cdots t_{n-1,n-2j+2}t_{0,n-2j+1})&=\ell(t_{n-j+1,n-j})+\cdots+ \ell(t_{n-1,n-2j+2})\\&\quad+\ell(t_{0,n-2j+1}).\end{align*} $$
$$ \begin{align*}\ell(t_{n-j+1,n-j}\cdots t_{n-1,n-2j+2}t_{0,n-2j+1})&=\ell(t_{n-j+1,n-j})+\cdots+ \ell(t_{n-1,n-2j+2})\\&\quad+\ell(t_{0,n-2j+1}).\end{align*} $$
Thus by Proposition 2.3 (cf. [Reference Shimada39, Section 3.3]), each element
![]() $gI$
in
$gI$
in
![]() $X_{w_j}(\tau ^2)^0$
is contained in a Schubert cell associated to
$X_{w_j}(\tau ^2)^0$
is contained in a Schubert cell associated to
![]() $t_{n-j+1,n-j}\cdots t_{n-1,n-2j+2}t_{0,n-2j+1}$
. By Lemma 5.1, it follows that
$t_{n-j+1,n-j}\cdots t_{n-1,n-2j+2}t_{0,n-2j+1}$
. By Lemma 5.1, it follows that
![]() $\pi (X_{w_j}(b)^0)$
is equal to the unique semi-module stratum of dimension j. This shows that the semi-module stratification of
$\pi (X_{w_j}(b)^0)$
is equal to the unique semi-module stratum of dimension j. This shows that the semi-module stratification of
![]() $X_{\mu }(b)$
is a refinement of the Ekedahl–Oort stratification.
$X_{\mu }(b)$
is a refinement of the Ekedahl–Oort stratification.
6.2 The Ekedahl–Oort stratification for
 $\omega _1+\omega _{n-2}$
$\omega _1+\omega _{n-2}$
Throughout this subsection, we set
![]() $\mu =\omega _1+\omega _{n-2}$
. Also we assume that
$\mu =\omega _1+\omega _{n-2}$
. Also we assume that
![]() $n\geq 4$
. Note that the unique dominant cocharacter
$n\geq 4$
. Note that the unique dominant cocharacter
![]() $\mu '$
with
$\mu '$
with
![]() $\mu '\prec \mu $
is
$\mu '\prec \mu $
is
![]() $\mu '=\omega _{n-1}$
. Clearly, we have
$\mu '=\omega _{n-1}$
. Clearly, we have
![]() ${^S\mathrm {Adm}}(\omega _{n-1})_{\operatorname {\mathrm {cyc}}}=\{\tau ^{n-1}\}$
and the semi-module stratification of
${^S\mathrm {Adm}}(\omega _{n-1})_{\operatorname {\mathrm {cyc}}}=\{\tau ^{n-1}\}$
and the semi-module stratification of
![]() $X_{\omega _{n-1}}(\tau ^{n-1})$
is a refinement of the Ekedahl–Oort stratification.
$X_{\omega _{n-1}}(\tau ^{n-1})$
is a refinement of the Ekedahl–Oort stratification.
Proposition 6.6 For any
![]() $1\le j\le n-2(=\dim X_\mu (b))$
, there exist exactly j elements of length
$1\le j\le n-2(=\dim X_\mu (b))$
, there exist exactly j elements of length
![]() $2j$
in
$2j$
in ![]() . Let
. Let
![]() $\varpi ^\mu y\in {^S\tilde W}$
be one of such elements. Then there exists
$\varpi ^\mu y\in {^S\tilde W}$
be one of such elements. Then there exists
![]() $v\in \operatorname {\mathrm {LP}}(\varpi ^\mu y)$
such that
$v\in \operatorname {\mathrm {LP}}(\varpi ^\mu y)$
such that
![]() $v^{-1}yv$
is a Coxeter element. Moreover,
$v^{-1}yv$
is a Coxeter element. Moreover,
![]() $X_w(b)=\emptyset $
for any
$X_w(b)=\emptyset $
for any
![]() $w\in {^S\mathrm {Adm}}(\mu )\setminus {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}$
, and the semi-module stratification of
$w\in {^S\mathrm {Adm}}(\mu )\setminus {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}$
, and the semi-module stratification of
![]() $X_{\mu }(b)$
is a refinement of the Ekedahl–Oort stratification.
$X_{\mu }(b)$
is a refinement of the Ekedahl–Oort stratification.
Proof We first prove by induction on n that there exist at least j elements of length
![]() $2j$
in
$2j$
in
![]() ${^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
, each of which has finite part y such that
${^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
, each of which has finite part y such that
![]() $ryr^{-1}$
is a Coxeter element for some
$ryr^{-1}$
is a Coxeter element for some
![]() $r\in W_{\{s_2,\ldots ,s_{n-2}\}}$
satisfying
$r\in W_{\{s_2,\ldots ,s_{n-2}\}}$
satisfying
![]() $r(\Phi _+\setminus \Phi _{\varpi ^\mu y})\subset \Phi _+$
(cf. Lemma 2.8). Note that if
$r(\Phi _+\setminus \Phi _{\varpi ^\mu y})\subset \Phi _+$
(cf. Lemma 2.8). Note that if
![]() $y\in W_0$
satisfies
$y\in W_0$
satisfies
then by [Reference Shimada39, Lemma 4.4], we have
![]() $\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )$
. In particular, since
$\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )$
. In particular, since
![]() $\ell (\varpi ^\mu )=3n-5$
,
$\ell (\varpi ^\mu )=3n-5$
,
![]() $\varpi ^\mu y$
is an element of length
$\varpi ^\mu y$
is an element of length
![]() $2j$
in
$2j$
in
![]() ${^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
for any n-cycle y of length
${^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
for any n-cycle y of length
![]() $3n-2j-5$
. If
$3n-2j-5$
. If
![]() $n=4$
, then
$n=4$
, then
![]() $s_1s_2s_3,s_2s_3s_1$
and
$s_1s_2s_3,s_2s_3s_1$
and
![]() $s_1s_2s_3s_1s_2$
are
$s_1s_2s_3s_1s_2$
are
![]() $4$
-cycles satisfying
$4$
-cycles satisfying
![]() $(\ast )$
. Moreover,
$(\ast )$
. Moreover,
![]() $s_2(s_1s_2s_3s_1s_2)s_2=s_1s_2s_3$
is a Coxeter element and
$s_2(s_1s_2s_3s_1s_2)s_2=s_1s_2s_3$
is a Coxeter element and
![]() $s_2(\Phi _+\setminus \Phi _{\varpi ^\mu s_1s_2s_3s_1s_2})\subset \Phi _+$
. So the claim is true for
$s_2(\Phi _+\setminus \Phi _{\varpi ^\mu s_1s_2s_3s_1s_2})\subset \Phi _+$
. So the claim is true for
![]() $n=4$
.
$n=4$
.
Suppose that
![]() $n\geq 5$
and the claim is true for
$n\geq 5$
and the claim is true for
![]() $n-1$
. Let y be a
$n-1$
. Let y be a
![]() $(n-1)$
-cycle in
$(n-1)$
-cycle in
![]() $W_{\{s_1,s_2,\ldots ,s_{n-2}\}}$
such that
$W_{\{s_1,s_2,\ldots ,s_{n-2}\}}$
such that
![]() $y^{-1}(2)<y^{-1}(3)<\cdots <y^{-1}(n-3)$
and
$y^{-1}(2)<y^{-1}(3)<\cdots <y^{-1}(n-3)$
and
![]() $y^{-1}(n-2)<y^{-1}(n-1)$
. Then
$y^{-1}(n-2)<y^{-1}(n-1)$
. Then ![]() satisfies
satisfies
![]() $(\ast )$
and
$(\ast )$
and
![]() $\ell (y')=\ell (y)+1$
. So by the induction hypothesis, there exist at least
$\ell (y')=\ell (y)+1$
. So by the induction hypothesis, there exist at least
![]() $j-1$
elements in
$j-1$
elements in
![]() $W_0$
which are n-cycles of length
$W_0$
which are n-cycles of length
![]() $3n-2j-5$
satisfying
$3n-2j-5$
satisfying
![]() $(\ast )$
. Note that for any
$(\ast )$
. Note that for any
![]() $r\in W_{\{s_2,\ldots ,s_{n-3}\}}$
, we have
$r\in W_{\{s_2,\ldots ,s_{n-3}\}}$
, we have
![]() $r'y'r^{\prime -1}=s_1(1\ 2\ \cdots \ n)ryr^{-1}(1\ 2\ \cdots \ n)^{-1}$
, where
$r'y'r^{\prime -1}=s_1(1\ 2\ \cdots \ n)ryr^{-1}(1\ 2\ \cdots \ n)^{-1}$
, where
![]() $r'=(1\ 2\ \cdots \ n)r(1\ 2\ \cdots \ n)^{-1}\in W_{\{s_2,\ldots ,s_{n-2}\}}$
. So again by the induction hypothesis, it is easy to verify that there exists
$r'=(1\ 2\ \cdots \ n)r(1\ 2\ \cdots \ n)^{-1}\in W_{\{s_2,\ldots ,s_{n-2}\}}$
. So again by the induction hypothesis, it is easy to verify that there exists
![]() $r\in W_{\{s_2,\ldots ,s_{n-3}\}}$
such that
$r\in W_{\{s_2,\ldots ,s_{n-3}\}}$
such that
![]() $r'y'r^{\prime -1}$
is a Coxeter element and
$r'y'r^{\prime -1}$
is a Coxeter element and
![]() $r'(\Phi _+\setminus \Phi _{\varpi ^\mu y'})\subset \Phi _+$
. Set
$r'(\Phi _+\setminus \Phi _{\varpi ^\mu y'})\subset \Phi _+$
. Set
![]() $c=s_{n-2}s_{n-1}s_{n-3}\cdots s_2s_1$
. It is easy to check that if n is odd (resp. even), then
$c=s_{n-2}s_{n-1}s_{n-3}\cdots s_2s_1$
. It is easy to check that if n is odd (resp. even), then
 $$ \begin{align*} c,\ cs_{n-2}s_{n-3},\ \ldots\ ,\ cs_{n-2}s_{n-3}\cdots s_2,\ &cs_{n-2}s_{n-3}\cdots s_2 s_3s_4,\ \ldots\ ,\\ &cs_{n-2}s_{n-3}\cdots s_2 s_3s_4\cdots s_{n-2}s_{n-1}\\ (\text{resp.\ }c,\ cs_{n-2}s_{n-3},\ \ldots\ ,\ cs_{n-2}s_{n-3}\cdots s_3,\ &cs_{n-2}s_{n-3}\cdots s_3 s_2s_3,\ \ldots\ ,\\ &cs_{n-2}s_{n-3}\cdots s_3 s_2s_3\cdots s_{n-2}s_{n-1}), \end{align*} $$
$$ \begin{align*} c,\ cs_{n-2}s_{n-3},\ \ldots\ ,\ cs_{n-2}s_{n-3}\cdots s_2,\ &cs_{n-2}s_{n-3}\cdots s_2 s_3s_4,\ \ldots\ ,\\ &cs_{n-2}s_{n-3}\cdots s_2 s_3s_4\cdots s_{n-2}s_{n-1}\\ (\text{resp.\ }c,\ cs_{n-2}s_{n-3},\ \ldots\ ,\ cs_{n-2}s_{n-3}\cdots s_3,\ &cs_{n-2}s_{n-3}\cdots s_3 s_2s_3,\ \ldots\ ,\\ &cs_{n-2}s_{n-3}\cdots s_3 s_2s_3\cdots s_{n-2}s_{n-1}), \end{align*} $$
are n-cycles satisfying
![]() $(\ast )$
. If
$(\ast )$
. If
![]() $y'$
is one of the elements above, then
$y'$
is one of the elements above, then
![]() $\Phi _{\{\chi _{2,3},\ldots ,\chi _{n-2,n-1}\}}\cap \Phi _+\subset \Phi _{\varpi ^\mu y'}$
and there exists
$\Phi _{\{\chi _{2,3},\ldots ,\chi _{n-2,n-1}\}}\cap \Phi _+\subset \Phi _{\varpi ^\mu y'}$
and there exists
![]() $r'\in W_{\{s_2,\ldots ,s_{n-2}\}}$
such that
$r'\in W_{\{s_2,\ldots ,s_{n-2}\}}$
such that
![]() $r'y'r^{\prime -1}$
is a Coxeter element. Thus, the claim is also true for n. By induction, our claim is true for any
$r'y'r^{\prime -1}$
is a Coxeter element. Thus, the claim is also true for n. By induction, our claim is true for any
![]() $n\geq 4$
.
$n\geq 4$
.
Clearly
![]() $\nu _w=\nu _b$
for any
$\nu _w=\nu _b$
for any
![]() $w\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
. Since
$w\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
. Since
![]() $b=\tau ^{n-1}$
is superbasic, the unique minimal length element in the
$b=\tau ^{n-1}$
is superbasic, the unique minimal length element in the
![]() $\sigma $
-cojugacy class of w is
$\sigma $
-cojugacy class of w is
![]() $\tau ^{n-1}$
(cf. [Reference He and Nie22, Proposition 3.5]). By Theorem 2.4, there exist a reduction tree
$\tau ^{n-1}$
(cf. [Reference He and Nie22, Proposition 3.5]). By Theorem 2.4, there exist a reduction tree
![]() $\mathcal T$
for w and a reduction path
$\mathcal T$
for w and a reduction path
![]() $\underline p$
in
$\underline p$
in
![]() $\mathcal T$
such that
$\mathcal T$
such that
![]() $\operatorname {\mathrm {end}}(\underline p)=\tau ^{n-1}$
and
$\operatorname {\mathrm {end}}(\underline p)=\tau ^{n-1}$
and
![]() $\ell _I(\underline p)=0$
. Thus by Lemma 2.1 and Proposition 2.6,
$\ell _I(\underline p)=0$
. Thus by Lemma 2.1 and Proposition 2.6,
![]() $|\pi (X_w(b)^{0,\sigma })|\geq q^{\frac {\ell (w)}{2}}$
for any
$|\pi (X_w(b)^{0,\sigma })|\geq q^{\frac {\ell (w)}{2}}$
for any
![]() $w\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
. By the comparison of
$w\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
. By the comparison of
![]() $|\sqcup _{w\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ }\pi (X_w(b)^{0,\sigma })|$
and
$|\sqcup _{w\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ }\pi (X_w(b)^{0,\sigma })|$
and
![]() $|X_\mu (b)^{0,\sigma }|$
, it follows from Lemma 5.3 and the claim we have shown above that there exist exactly j elements of length
$|X_\mu (b)^{0,\sigma }|$
, it follows from Lemma 5.3 and the claim we have shown above that there exist exactly j elements of length
![]() $2j$
in
$2j$
in
![]() ${^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
. Moreover, it follows that
${^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
. Moreover, it follows that
![]() $\pi (X_w(b)^0)$
is irreducible of dimension
$\pi (X_w(b)^0)$
is irreducible of dimension
![]() $\frac {\ell (w)}{2}$
for any
$\frac {\ell (w)}{2}$
for any
![]() $w\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
and that
$w\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
and that
![]() $X_w(b)=\emptyset $
for any
$X_w(b)=\emptyset $
for any
![]() $w\in {^S\mathrm {Adm}}(\mu )\setminus {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}$
.
$w\in {^S\mathrm {Adm}}(\mu )\setminus {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}$
.
It remains to show that the semi-module stratification of
![]() $X_{\mu }(b)$
is a refinement of the Ekedahl–Oort stratification. We prove that for any
$X_{\mu }(b)$
is a refinement of the Ekedahl–Oort stratification. We prove that for any
![]() $w\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
, there exists an extended semi-module
$w\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
, there exists an extended semi-module
![]() $(A^\lambda ,\varphi )$
for
$(A^\lambda ,\varphi )$
for
![]() $\mu $
such that
$\mu $
such that
![]() $\pi (X_w(b)^0)=S_{A^\lambda ,\varphi }(=X_\mu ^\lambda (b)$
by Lemmas 3.9 and 5.3). We argue by induction on
$\pi (X_w(b)^0)=S_{A^\lambda ,\varphi }(=X_\mu ^\lambda (b)$
by Lemmas 3.9 and 5.3). We argue by induction on
![]() $\ell (w)$
. If
$\ell (w)$
. If
![]() $\ell (w)=2$
, i.e.,
$\ell (w)=2$
, i.e.,
![]() $w=\varpi ^\mu cs_{n-2}s_{n-3}\cdots s_2 s_3s_4\cdots s_{n-2}s_{n-1}=s_0s_{n-1}\tau ^{n-1}$
, then
$w=\varpi ^\mu cs_{n-2}s_{n-3}\cdots s_2 s_3s_4\cdots s_{n-2}s_{n-1}=s_0s_{n-1}\tau ^{n-1}$
, then
![]() $w\rightarrow _{\sigma } s_0ws_0=\tau ^{n-1}$
. It easily follows from Theorem 2.9 that
$w\rightarrow _{\sigma } s_0ws_0=\tau ^{n-1}$
. It easily follows from Theorem 2.9 that
![]() $X_{\tau ^{n-1}s_0}(b)=\emptyset $
. So by Proposition 2.3, we have
$X_{\tau ^{n-1}s_0}(b)=\emptyset $
. So by Proposition 2.3, we have
![]() $X_w(b)^0=Is_0I/I$
and hence
$X_w(b)^0=Is_0I/I$
and hence
![]() $\pi (X_w(b)^0)=X_\mu ^{\chi _{1,n}^\vee }(b)$
.
$\pi (X_w(b)^0)=X_\mu ^{\chi _{1,n}^\vee }(b)$
.
Suppose that
![]() $\ell (w)\geq 4$
and the claim is true for any
$\ell (w)\geq 4$
and the claim is true for any
![]() $w'\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
with
$w'\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
with
![]() $\ell (w')<\ell (w)$
. Since
$\ell (w')<\ell (w)$
. Since
![]() $\pi (X_w(b)^0)$
is irreducible of dimension
$\pi (X_w(b)^0)$
is irreducible of dimension
![]() $\frac {\ell (w)}{2}$
, there exists a unique extended semi-module
$\frac {\ell (w)}{2}$
, there exists a unique extended semi-module
![]() $(A^\lambda ,\varphi )$
for
$(A^\lambda ,\varphi )$
for
![]() $\mu $
such that
$\mu $
such that
![]() $\dim (\pi (X_w(b)^0)\cap S_{A^\lambda ,\varphi })=\frac {\ell (w)}{2}$
. Also,
$\dim (\pi (X_w(b)^0)\cap S_{A^\lambda ,\varphi })=\frac {\ell (w)}{2}$
. Also,
![]() $\pi (X_w(b)^0)\cap S_{A^\lambda ,\varphi }$
is open in both
$\pi (X_w(b)^0)\cap S_{A^\lambda ,\varphi }$
is open in both
![]() $\pi (X_w(b)^0)$
and
$\pi (X_w(b)^0)$
and
![]() $S_{A^\lambda ,\varphi }$
. So the closure of
$S_{A^\lambda ,\varphi }$
. So the closure of
![]() $\pi (X_w(b)^0)\cap S_{A^\lambda ,\varphi }$
in
$\pi (X_w(b)^0)\cap S_{A^\lambda ,\varphi }$
in
![]() $X_\mu (b)$
is equal to both the closure of
$X_\mu (b)$
is equal to both the closure of
![]() $\pi (X_w(b)^0)$
and
$\pi (X_w(b)^0)$
and
![]() $S_{A^\lambda ,\varphi }$
in
$S_{A^\lambda ,\varphi }$
in
![]() $X_\mu (b)$
. By [Reference He20, Proposition 2.6] (see also [Reference Görtz and He11, Section 3.3]), the closure of
$X_\mu (b)$
. By [Reference He20, Proposition 2.6] (see also [Reference Görtz and He11, Section 3.3]), the closure of
![]() $\pi (X_w(b)^0)$
is contained in
$\pi (X_w(b)^0)$
is contained in
Here we write
![]() $w'\le _S w$
if there exists
$w'\le _S w$
if there exists
![]() $x\in W_0$
such that
$x\in W_0$
such that
![]() $xw'x^{-1}\le w$
. By the above description of the finite part of each element in
$xw'x^{-1}\le w$
. By the above description of the finite part of each element in
![]() ${^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
, it is easily checked that if
${^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
, it is easily checked that if
![]() $w'\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
and
$w'\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
and
![]() $\ell (w)=\ell (w')$
, then there is no
$\ell (w)=\ell (w')$
, then there is no
![]() $x\in W_0$
such that
$x\in W_0$
such that
![]() $xwx^{-1}=w'$
. So if
$xwx^{-1}=w'$
. So if
![]() $w'\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ , w'\le _S w$
and
$w'\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ , w'\le _S w$
and
![]() $\ell (w')=\ell (w)$
, then
$\ell (w')=\ell (w)$
, then
![]() $w=w'$
. Thus, by the induction hypothesis, we have
$w=w'$
. Thus, by the induction hypothesis, we have
![]() $S_{A^\lambda ,\varphi }\subseteq \pi (X_w(b)^0)$
. By [Reference Chen and Viehmann2, Propositions 2.11(5) and 3.4], the closure of
$S_{A^\lambda ,\varphi }\subseteq \pi (X_w(b)^0)$
. By [Reference Chen and Viehmann2, Propositions 2.11(5) and 3.4], the closure of
![]() $S_{A^\lambda ,\varphi }$
is contained in a union of semi-module strata
$S_{A^\lambda ,\varphi }$
is contained in a union of semi-module strata
![]() $T_\lambda $
such that
$T_\lambda $
such that
![]() $\dim (T_\lambda \setminus S_{A^\lambda ,\varphi })<\dim S_{A^\lambda ,\varphi }$
. Thus, by the induction hypothesis and Lemma 5.3, we have
$\dim (T_\lambda \setminus S_{A^\lambda ,\varphi })<\dim S_{A^\lambda ,\varphi }$
. Thus, by the induction hypothesis and Lemma 5.3, we have
![]() $\pi (X_w(b)^0)\subseteq S_{A^\lambda ,\varphi }$
. Therefore, it follows that
$\pi (X_w(b)^0)\subseteq S_{A^\lambda ,\varphi }$
. Therefore, it follows that
![]() $\pi (X_w(b)^0)=S_{A^\lambda ,\varphi }$
, which completes the proof.
$\pi (X_w(b)^0)=S_{A^\lambda ,\varphi }$
, which completes the proof.
6.3 The Ekedahl–Oort stratification for
 $\omega _1+\omega _{n-3}$
$\omega _1+\omega _{n-3}$
Throughout this subsection, we set
![]() $\mu =\omega _1+\omega _{n-3}$
. Also we assume that
$\mu =\omega _1+\omega _{n-3}$
. Also we assume that
![]() $n\geq 7$
. Note that the unique dominant cocharacter
$n\geq 7$
. Note that the unique dominant cocharacter
![]() $\mu '$
with
$\mu '$
with
![]() $\mu '\prec \mu $
is
$\mu '\prec \mu $
is
![]() $\mu '=\omega _{n-2}$
.
$\mu '=\omega _{n-2}$
.
Proposition 6.7 There exist at least
![]() $2(n-4)$
elements of length
$2(n-4)$
elements of length
![]() $3n-11$
in
$3n-11$
in ![]() . There also exists an element w of length
. There also exists an element w of length
![]() $3n-14$
in
$3n-14$
in
![]() ${^S\mathrm {Adm}}(\mu )$
such that
${^S\mathrm {Adm}}(\mu )$
such that
![]() $p(w)$
is not a n-cycle and
$p(w)$
is not a n-cycle and
![]() $X_w(b)\neq \emptyset $
. Moreover, the semi-module stratification of
$X_w(b)\neq \emptyset $
. Moreover, the semi-module stratification of
![]() $X_\mu (b)$
is not a refinement of the Ekedahl–Oort stratification.
$X_\mu (b)$
is not a refinement of the Ekedahl–Oort stratification.
Proof For any
![]() $1\le j\le n-4$
, set
$1\le j\le n-4$
, set
![]() $c_j=s_{n-3}s_{n-2}s_{n-1}s_{n-4}\cdots s_{j+2}s_{j+1}s_1\cdots s_{j-1}s_j$
. For
$c_j=s_{n-3}s_{n-2}s_{n-1}s_{n-4}\cdots s_{j+2}s_{j+1}s_1\cdots s_{j-1}s_j$
. For
![]() $j=n-3$
, set
$j=n-3$
, set
![]() $c_{n-3}=s_1s_2\cdots s_{n-1}$
. Then we have
$c_{n-3}=s_1s_2\cdots s_{n-1}$
. Then we have
![]() $\varpi ^\mu c_j\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
and
$\varpi ^\mu c_j\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
and
![]() $\ell (\varpi ^\mu c_j)=3n-9$
for any
$\ell (\varpi ^\mu c_j)=3n-9$
for any
![]() $1\le j\le n-3$
. If
$1\le j\le n-3$
. If
![]() $1\le j\le n-5$
, then
$1\le j\le n-5$
, then
![]() $c_js_{n-3}s_{n-2}$
and
$c_js_{n-3}s_{n-2}$
and
![]() $c_js_{n-3}s_{n-4}$
are n-cycles of length
$c_js_{n-3}s_{n-4}$
are n-cycles of length
![]() $3n-11$
satisfying
$3n-11$
satisfying
![]() $\varpi ^\mu c_js_{n-3}s_{n-2},\varpi ^\mu c_js_{n-3}s_{n-4}\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
. Further
$\varpi ^\mu c_js_{n-3}s_{n-2},\varpi ^\mu c_js_{n-3}s_{n-4}\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
. Further
![]() $c_{n-4}s_{n-3}s_{n-2}$
and
$c_{n-4}s_{n-3}s_{n-2}$
and
![]() $c_{n-3}s_{n-4}s_{n-3}$
are also n-cycles of length
$c_{n-3}s_{n-4}s_{n-3}$
are also n-cycles of length
![]() $3n-11$
satisfying
$3n-11$
satisfying
![]() $\varpi ^\mu c_{n-4}s_{n-3}s_{n-2},\varpi ^\mu c_{n-3}s_{n-4}s_{n-3}\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
. Thus, we have found
$\varpi ^\mu c_{n-4}s_{n-3}s_{n-2},\varpi ^\mu c_{n-3}s_{n-4}s_{n-3}\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
. Thus, we have found
![]() $2(n-4)$
distinct elements of length
$2(n-4)$
distinct elements of length
![]() $3n-11$
in
$3n-11$
in
![]() ${^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
.
${^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
.
Set
![]() $y=c_{n-5}s_{n-3}s_{n-2}s_{n-4}s_{n-6}s_{n-5}=(1\ 2\ \cdots \ n-6\ n-2\ n\ n-3)(n-4\ n-5\ n-1)$
. Then
$y=c_{n-5}s_{n-3}s_{n-2}s_{n-4}s_{n-6}s_{n-5}=(1\ 2\ \cdots \ n-6\ n-2\ n\ n-3)(n-4\ n-5\ n-1)$
. Then
![]() $\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )$
and
$\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )$
and
![]() $\chi _{1,n-1},\chi _{n-5,n}\in \Phi _+\setminus \Phi _{\varpi ^\mu y}$
. By Theorem 2.9,
$\chi _{1,n-1},\chi _{n-5,n}\in \Phi _+\setminus \Phi _{\varpi ^\mu y}$
. By Theorem 2.9,
![]() $X_{\varpi ^\mu y}(b)\neq \emptyset $
. This shows the second assertion. We can easily check the last assertion using Lemma 5.4, similarly as the proof of Proposition 6.4.
$X_{\varpi ^\mu y}(b)\neq \emptyset $
. This shows the second assertion. We can easily check the last assertion using Lemma 5.4, similarly as the proof of Proposition 6.4.
6.4 The Ekedahl–Oort stratification for
 $\omega _1+\omega _2,\omega _4+\omega _{n-1}$
$\omega _1+\omega _2,\omega _4+\omega _{n-1}$
Note that the unique dominant cocharacter
![]() $\mu '$
with
$\mu '$
with
![]() $\mu '\prec \omega _1+\omega _2$
is
$\mu '\prec \omega _1+\omega _2$
is
![]() $\omega _3$
. By an explicit calculation, it is easy to verify the following statements (cf. Proposition 6.5).
$\omega _3$
. By an explicit calculation, it is easy to verify the following statements (cf. Proposition 6.5).
Proposition 6.8 Assume that
![]() $n=5$
. Set
$n=5$
. Set
![]() $\mu =\omega _1+\omega _2$
. For any
$\mu =\omega _1+\omega _2$
. For any
![]() $1\le j\le 3(=\dim X_\mu (b))$
, set
$1\le j\le 3(=\dim X_\mu (b))$
, set ![]() . Then we have
. Then we have
Let
![]() $\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
. Then there exists
$\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}^\circ $
. Then there exists
![]() $v\in \operatorname {\mathrm {LP}}(\varpi ^\mu y)$
such that
$v\in \operatorname {\mathrm {LP}}(\varpi ^\mu y)$
such that
![]() $v^{-1}yv$
is a Coxeter element. Moreover,
$v^{-1}yv$
is a Coxeter element. Moreover,
![]() $X_w(b)=\emptyset $
for any
$X_w(b)=\emptyset $
for any
![]() $w\in {^S\mathrm {Adm}}(\mu )\setminus {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}$
, and the semi-module stratification of
$w\in {^S\mathrm {Adm}}(\mu )\setminus {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}$
, and the semi-module stratification of
![]() $X_{\mu }(b)$
is a refinement of the Ekedahl–Oort stratification.
$X_{\mu }(b)$
is a refinement of the Ekedahl–Oort stratification.
Lemma 6.9 Assume that
![]() $n=7$
or
$n=7$
or
![]() $8$
. Let
$8$
. Let
![]() $\mu $
be
$\mu $
be
![]() $\omega _1+\omega _2$
(resp.
$\omega _1+\omega _2$
(resp.
![]() $\omega _4+\omega _{n-1}$
). Set
$\omega _4+\omega _{n-1}$
). Set
![]() $c=s_1s_2\cdots s_{n-1}$
. Then
$c=s_1s_2\cdots s_{n-1}$
. Then
![]() $\varpi ^\mu cs_1s_2s_3\in {^S\mathrm {Adm}}(\mu )$
and
$\varpi ^\mu cs_1s_2s_3\in {^S\mathrm {Adm}}(\mu )$
and
![]() $X_{\varpi ^\mu cs_1s_2s_3}(b)\neq \emptyset $
(resp.
$X_{\varpi ^\mu cs_1s_2s_3}(b)\neq \emptyset $
(resp.
![]() $\varpi ^\mu c^{-1}s_5s_4s_3\in {^S\mathrm {Adm}}(\mu )$
and
$\varpi ^\mu c^{-1}s_5s_4s_3\in {^S\mathrm {Adm}}(\mu )$
and
![]() $X_{\varpi ^\mu c^{-1}s_5s_4s_3}(b)\neq \emptyset $
). Further
$X_{\varpi ^\mu c^{-1}s_5s_4s_3}(b)\neq \emptyset $
). Further
![]() $cs_1s_2s_3$
(resp.
$cs_1s_2s_3$
(resp.
![]() $c^{-1}s_5s_4s_3$
) is not n-cycle.
$c^{-1}s_5s_4s_3$
) is not n-cycle.
6.5 The Ekedahl–Oort stratification for
 $\omega _2+\omega _{n-3}$
$\omega _2+\omega _{n-3}$
We set
![]() $\mu =\omega _2+\omega _{n-3}$
. Also we assume that
$\mu =\omega _2+\omega _{n-3}$
. Also we assume that
![]() $n\geq 5$
.
$n\geq 5$
.
Lemma 6.10 If n is odd (resp. even), set
![]() $y=s_2s_3\cdots s_{n-3}s_1s_2\cdots s_{n-3}$
(resp.
$y=s_2s_3\cdots s_{n-3}s_1s_2\cdots s_{n-3}$
(resp.
![]() $y=s_2s_3\cdots s_{n-3}s_1s_2\cdots s_{n-2}$
). Then
$y=s_2s_3\cdots s_{n-3}s_1s_2\cdots s_{n-2}$
). Then
![]() $\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu ),X_{\varpi ^\mu y}(b)\neq \emptyset $
and y is not a n-cycle.
$\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu ),X_{\varpi ^\mu y}(b)\neq \emptyset $
and y is not a n-cycle.
Proof If n is odd (resp. even), then
![]() $y=(1\ 3\ \cdots \ n-2)(2\ 4\ \ \cdots \ n-1\ n)$
(resp.
$y=(1\ 3\ \cdots \ n-2)(2\ 4\ \ \cdots \ n-1\ n)$
(resp.
![]() $(1\ 3\ \cdots \ n-1)(2\ 4\ \cdots \ n)$
) and
$(1\ 3\ \cdots \ n-1)(2\ 4\ \cdots \ n)$
) and
![]() $\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )$
. Note that
$\varpi ^\mu y\in {^S\mathrm {Adm}}(\mu )$
. Note that
![]() $\chi _{1,n},\chi _{2,n-1}\in \Phi _+\setminus \Phi _{\varpi ^\mu y}$
. So by Lemma 2.9,
$\chi _{1,n},\chi _{2,n-1}\in \Phi _+\setminus \Phi _{\varpi ^\mu y}$
. So by Lemma 2.9,
![]() $X_{\varpi ^\mu y}(b)\neq \emptyset $
. The proof is finished.
$X_{\varpi ^\mu y}(b)\neq \emptyset $
. The proof is finished.
7 Comparison of two stratifications
Keep the notations and assumptions in Section 3 .
7.1 Known cases
The following results are known in (the proof of) [Reference Shimada39, Corollary 5.5 and Theorem 5.9].
Proposition 7.1 Let
![]() $\cong $
denote a universal homeomorphism.
$\cong $
denote a universal homeomorphism.
-
(i) Assume that
 $n\geq 3$
. Set
$n\geq 3$
. Set
 $\mu =2\omega _1, w=\varpi ^\mu s_1s_2\cdots s_{n-1}$
and
$\mu =2\omega _1, w=\varpi ^\mu s_1s_2\cdots s_{n-1}$
and  $$ \begin{align*} \lambda=\begin{cases} \chi_{2,n-1}^\vee+\chi_{4,n-3}^\vee+\cdots+\chi_{\frac{n-1}{2},\frac{n+3}{2}}^\vee & (\frac{n-1}{2}\ \mathrm{even})\\ \chi_{1,n}^\vee+\chi_{3,n-2}^\vee+\cdots+\chi_{\frac{n-1}{2},\frac{n+3}{2}}^\vee & (\frac{n-1}{2}\ \mathrm{odd}). \end{cases} \end{align*} $$
$$ \begin{align*} \lambda=\begin{cases} \chi_{2,n-1}^\vee+\chi_{4,n-3}^\vee+\cdots+\chi_{\frac{n-1}{2},\frac{n+3}{2}}^\vee & (\frac{n-1}{2}\ \mathrm{even})\\ \chi_{1,n}^\vee+\chi_{3,n-2}^\vee+\cdots+\chi_{\frac{n-1}{2},\frac{n+3}{2}}^\vee & (\frac{n-1}{2}\ \mathrm{odd}). \end{cases} \end{align*} $$
Then we have
 $X_\mu (b)^0=X_\mu ^\lambda (b)=\pi (X_w(b)^0)\cong \mathbb A^{\frac {n-1}{2}}$
.
$X_\mu (b)^0=X_\mu ^\lambda (b)=\pi (X_w(b)^0)\cong \mathbb A^{\frac {n-1}{2}}$
. -
(ii) Assume that
 $n\geq 3$
. Set
$n\geq 3$
. Set
 $\mu =2\omega _1+\omega _{n-1},w_j=\varpi ^\mu s_{n-1}s_{n-2}\cdots s_{n-j+1}s_1s_2\cdots s_{n-j}$
and for
$\mu =2\omega _1+\omega _{n-1},w_j=\varpi ^\mu s_{n-1}s_{n-2}\cdots s_{n-j+1}s_1s_2\cdots s_{n-j}$
and for $$ \begin{align*} \lambda_j=\begin{cases} \chi_{1,2j}^\vee+\chi_{2,2j-1}^\vee+\cdots+\chi_{j,j+1}^\vee & (j\le \frac{n}{2})\\ \chi_{2j+1-n,n}^\vee+\chi_{2j+2-n,n-1}^\vee+\cdots+\chi_{j,j+1}^\vee & (j\geq \frac{n}{2}). \end{cases} \end{align*} $$
$$ \begin{align*} \lambda_j=\begin{cases} \chi_{1,2j}^\vee+\chi_{2,2j-1}^\vee+\cdots+\chi_{j,j+1}^\vee & (j\le \frac{n}{2})\\ \chi_{2j+1-n,n}^\vee+\chi_{2j+2-n,n-1}^\vee+\cdots+\chi_{j,j+1}^\vee & (j\geq \frac{n}{2}). \end{cases} \end{align*} $$
 $j=1,2,\ldots ,n-1$
. Then we have
$j=1,2,\ldots ,n-1$
. Then we have
 $X_\mu (b)^0=\bigsqcup _{1\le j\le n-1} X_\mu ^{\lambda _j}(b)$
and
$X_\mu (b)^0=\bigsqcup _{1\le j\le n-1} X_\mu ^{\lambda _j}(b)$
and
 $X_\mu ^{\lambda _j}(b)=\pi (X_{w_j}(b)^0)\cong \mathbb A^{n-1}$
for each j.
$X_\mu ^{\lambda _j}(b)=\pi (X_{w_j}(b)^0)\cong \mathbb A^{n-1}$
for each j.
-
(iii) Assume that
 $n=5$
. Set
$n=5$
. Set
 $\mu =3\omega _1, w=\varpi ^\mu s_1s_2s_3s_4$
and
$\mu =3\omega _1, w=\varpi ^\mu s_1s_2s_3s_4$
and
 $\lambda =\chi _{1,2}^\vee +\chi _{3,4}^\vee $
. Then we have
$\lambda =\chi _{1,2}^\vee +\chi _{3,4}^\vee $
. Then we have
 $X_\mu (b)^0=X_\mu ^\lambda (b)=\pi (X_w(b)^0)\cong \mathbb A^4$
.
$X_\mu (b)^0=X_\mu ^\lambda (b)=\pi (X_w(b)^0)\cong \mathbb A^4$
. -
(iv) Assume that
 $n=4$
. Set
$n=4$
. Set
 $\mu =3\omega _1, w=\varpi ^\mu s_1s_2s_3$
and
$\mu =3\omega _1, w=\varpi ^\mu s_1s_2s_3$
and
 $\lambda =\chi _{3,2}^\vee $
. Then we have
$\lambda =\chi _{3,2}^\vee $
. Then we have
 $X_\mu (b)^0=X_\mu ^\lambda (b)=\pi (X_w(b)^0)\cong \mathbb A^3$
.
$X_\mu (b)^0=X_\mu ^\lambda (b)=\pi (X_w(b)^0)\cong \mathbb A^3$
. -
(v) Assume that
 $n=3$
. Set
$n=3$
. Set
 $\mu =4\omega _1, w=\varpi ^\mu s_1s_2$
and
$\mu =4\omega _1, w=\varpi ^\mu s_1s_2$
and
 $\lambda =\chi _{3,1}^\vee $
. Then we have
$\lambda =\chi _{3,1}^\vee $
. Then we have
 $X_\mu (b)^0=X_\mu ^\lambda (b)=\pi (X_w(b)^0)\cong \mathbb A^3$
.
$X_\mu (b)^0=X_\mu ^\lambda (b)=\pi (X_w(b)^0)\cong \mathbb A^3$
. -
(vi) Assume that
 $n=3$
. Set
$n=3$
. Set
 $\mu =3\omega _1+\omega _2, w_1=\varpi ^\mu s_1s_2,w_2=\varpi ^\mu s_2s_1,\lambda _1=\chi _{2,3}^\vee $
and
$\mu =3\omega _1+\omega _2, w_1=\varpi ^\mu s_1s_2,w_2=\varpi ^\mu s_2s_1,\lambda _1=\chi _{2,3}^\vee $
and
 $\lambda _2=\chi _{3,2}^\vee $
. Then we have
$\lambda _2=\chi _{3,2}^\vee $
. Then we have
 $X_\mu (b)^0=X_\mu ^{\lambda _1}(b)\sqcup X_\mu ^{\lambda _2}(b)$
and
$X_\mu (b)^0=X_\mu ^{\lambda _1}(b)\sqcup X_\mu ^{\lambda _2}(b)$
and
 $X_\mu ^{\lambda _j}(b)=\pi (X_{w_j}(b)^0)\cong \mathbb A^3$
for each j.
$X_\mu ^{\lambda _j}(b)=\pi (X_{w_j}(b)^0)\cong \mathbb A^3$
for each j. -
(vii) Assume that
 $n=2$
. Set
$n=2$
. Set
 $\mu =m\omega _1$
with
$\mu =m\omega _1$
with
 $m\geq 1$
,
$m\geq 1$
,
 $w=\varpi ^\mu s_1$
and
$w=\varpi ^\mu s_1$
and  $$ \begin{align*}\lambda=\begin{cases} \frac{m-1}{2}\chi_{1,2}^\vee & (\frac{m-1}{2}\ \mathrm{odd})\\ \frac{m-1}{2}\chi_{2,1}^\vee & (\frac{m-1}{2}\ \mathrm{even}). \end{cases}\end{align*} $$
$$ \begin{align*}\lambda=\begin{cases} \frac{m-1}{2}\chi_{1,2}^\vee & (\frac{m-1}{2}\ \mathrm{odd})\\ \frac{m-1}{2}\chi_{2,1}^\vee & (\frac{m-1}{2}\ \mathrm{even}). \end{cases}\end{align*} $$
Then we have
 $X_\mu (b)^0=X_\mu ^\lambda (b)=\pi (X_w(b)^0)\cong \mathbb A^{\frac {m-1}{2}}$
.
$X_\mu (b)^0=X_\mu ^\lambda (b)=\pi (X_w(b)^0)\cong \mathbb A^{\frac {m-1}{2}}$
.
7.2 Proof of the main theorem
Theorem 7.2 Let
![]() $\mu \in X_*(T)_+$
. The following assertions are equivalent.
$\mu \in X_*(T)_+$
. The following assertions are equivalent.
-
(i) The semi-module stratification of
 $X_{\preceq \mu }(b)$
gives a refinement of the Ekedahl–Oort stratification.
$X_{\preceq \mu }(b)$
gives a refinement of the Ekedahl–Oort stratification. -
(ii) For any
 $w\in {^S{\operatorname {\mathrm {Adm}}}}(\mu )$
with
$w\in {^S{\operatorname {\mathrm {Adm}}}}(\mu )$
with
 $X_w(b)\neq \emptyset $
, there exists
$X_w(b)\neq \emptyset $
, there exists
 $v\in \operatorname {\mathrm {LP}}(w)$
such that
$v\in \operatorname {\mathrm {LP}}(w)$
such that
 $v^{-1}p(w)v$
is a Coxeter element.
$v^{-1}p(w)v$
is a Coxeter element. -
(iii) The cocharacter
 $\mu $
has one of the following forms:
$\mu $
has one of the following forms:  $$ \begin{align*} &\omega_1,\quad \omega_{n-1},\ &(n\geq 1),\\ &\omega_2,\quad 2\omega_1,\quad \omega_{n-2},\quad 2\omega_{n-1},\ &(\mathrm{odd}\ n\geq 3),\\ &\omega_2+\omega_{n-1},\quad 2\omega_1+\omega_{n-1}\quad \omega_1+\omega_{n-2},\quad\omega_1+2\omega_{n-1},\ &(n\geq 3),\\ &\omega_3,\quad\omega_{n-3},\ &(n=7,8),\\ &3\omega_1,\quad 3\omega_{n-1},\ &(n=4,5),\\ &\omega_1+\omega_2,\quad\omega_3+\omega_4,\ &(n=5),\\ &4\omega_1,\quad \omega_1+3\omega_2,\quad 4\omega_2,\quad 3\omega_1+\omega_2, &(n=3),\\ &m\omega_1\ \mathrm{with}\ m\ \mathrm{odd,} &(n=2). \end{align*} $$
$$ \begin{align*} &\omega_1,\quad \omega_{n-1},\ &(n\geq 1),\\ &\omega_2,\quad 2\omega_1,\quad \omega_{n-2},\quad 2\omega_{n-1},\ &(\mathrm{odd}\ n\geq 3),\\ &\omega_2+\omega_{n-1},\quad 2\omega_1+\omega_{n-1}\quad \omega_1+\omega_{n-2},\quad\omega_1+2\omega_{n-1},\ &(n\geq 3),\\ &\omega_3,\quad\omega_{n-3},\ &(n=7,8),\\ &3\omega_1,\quad 3\omega_{n-1},\ &(n=4,5),\\ &\omega_1+\omega_2,\quad\omega_3+\omega_4,\ &(n=5),\\ &4\omega_1,\quad \omega_1+3\omega_2,\quad 4\omega_2,\quad 3\omega_1+\omega_2, &(n=3),\\ &m\omega_1\ \mathrm{with}\ m\ \mathrm{odd,} &(n=2). \end{align*} $$
If one of the above conditions holds, then for any
![]() $w\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}$
, there exist
$w\in {^S\mathrm {Adm}}(\mu )_{\operatorname {\mathrm {cyc}}}$
, there exist
![]() $\mu '\in X_*(T)_+$
with
$\mu '\in X_*(T)_+$
with
![]() $\mu '\preceq \mu $
and a cyclic extended semi-module
$\mu '\preceq \mu $
and a cyclic extended semi-module
![]() $(A^\lambda ,\varphi )$
for
$(A^\lambda ,\varphi )$
for
![]() $\mu '$
such that
$\mu '$
such that
![]() $\pi (X_w(b)^0)=X_{\preceq \mu }^\lambda (b)=S_{A^\lambda ,\varphi }$
. Moreover,
$\pi (X_w(b)^0)=X_{\preceq \mu }^\lambda (b)=S_{A^\lambda ,\varphi }$
. Moreover,
![]() $\pi (X_w(b)^0)\cong \mathbb A^{\mathcal V(A^\lambda ,\varphi )}$
.
$\pi (X_w(b)^0)\cong \mathbb A^{\mathcal V(A^\lambda ,\varphi )}$
.
Proof For any
![]() $w=\varpi ^\mu y\in {^S\tilde W}$
with
$w=\varpi ^\mu y\in {^S\tilde W}$
with
![]() $\mu $
dominant, set
$\mu $
dominant, set
![]() $w^*=\varpi ^{(\mu (1),\ldots ,\mu (1))}\varsigma (w)$
(cf. Section 2.5 and Section 3.2). Then
$w^*=\varpi ^{(\mu (1),\ldots ,\mu (1))}\varsigma (w)$
(cf. Section 2.5 and Section 3.2). Then
![]() $w^*\in {^S\tilde W}$
and
$w^*\in {^S\tilde W}$
and
![]() $p(w^*)=w_{\max }yw_{\max }^{-1}$
(cf. Section 2.5 and Section 3.2). Note that the arguments and results in Section 5 and Section 6 for
$p(w^*)=w_{\max }yw_{\max }^{-1}$
(cf. Section 2.5 and Section 3.2). Note that the arguments and results in Section 5 and Section 6 for
![]() $(\mu ,w,b)$
also hold for
$(\mu ,w,b)$
also hold for
![]() $(\mu ^*,w^*,b^*)$
. Thus, in this proof, it suffices to treat the case for either
$(\mu ^*,w^*,b^*)$
. Thus, in this proof, it suffices to treat the case for either
![]() $\mu $
or
$\mu $
or
![]() $\mu ^*$
.
$\mu ^*$
.
First assume that
![]() $n\geq 6$
. Let
$n\geq 6$
. Let
![]() $1\le m_0<n$
be the residue of m modulo n. If
$1\le m_0<n$
be the residue of m modulo n. If
![]() $4\le m_0\le n-4$
, then
$4\le m_0\le n-4$
, then
![]() $\omega _{m_0}+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
. So by Lemma 6.1 and Proposition 6.4,
$\omega _{m_0}+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
. So by Lemma 6.1 and Proposition 6.4,
![]() $\mu $
satisfies neither (i) nor (ii). If
$\mu $
satisfies neither (i) nor (ii). If
![]() $n\geq 10$
and
$n\geq 10$
and
![]() $m_0=3$
, then by Lemma 6.2,
$m_0=3$
, then by Lemma 6.2,
![]() $\mu $
satisfies neither (i) nor (ii). If
$\mu $
satisfies neither (i) nor (ii). If
![]() $n=7,8$
and
$n=7,8$
and
![]() $m_0=3$
, then by Proposition 6.5,
$m_0=3$
, then by Proposition 6.5,
![]() $\mu =\omega _3$
satisfies (i) and (ii). If, moreover,
$\mu =\omega _3$
satisfies (i) and (ii). If, moreover,
![]() $\mu \neq \omega _3$
, then
$\mu \neq \omega _3$
, then
![]() $\omega _1+\omega _2+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
or
$\omega _1+\omega _2+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
or
![]() $\omega _4+\omega _{n-1}+(\lfloor \frac {m}{n} \rfloor -1)\omega _n\preceq \mu $
. So by Lemma 5.6 and Lemma 6.9,
$\omega _4+\omega _{n-1}+(\lfloor \frac {m}{n} \rfloor -1)\omega _n\preceq \mu $
. So by Lemma 5.6 and Lemma 6.9,
![]() $\mu $
satisfies neither (i) nor (ii). If
$\mu $
satisfies neither (i) nor (ii). If
![]() $m_0=n-2$
, then
$m_0=n-2$
, then
![]() $\omega _1+\omega _{n-3}+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
unless
$\omega _1+\omega _{n-3}+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
unless
![]() $\mu =\omega _{n-2}$
or
$\mu =\omega _{n-2}$
or
![]() $2\omega _{n-1}$
. If
$2\omega _{n-1}$
. If
![]() $m_0=n-1$
, then
$m_0=n-1$
, then
![]() $\omega _2+\omega _{n-3}+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
unless
$\omega _2+\omega _{n-3}+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
unless
![]() $\mu =\omega _{n-1},\omega _1+\omega _{n-2}$
or
$\mu =\omega _{n-1},\omega _1+\omega _{n-2}$
or
![]() $\omega _1+2\omega _{n-1}$
. Thus, the equivalence of (i), (ii) and (iii) for
$\omega _1+2\omega _{n-1}$
. Thus, the equivalence of (i), (ii) and (iii) for
![]() $m_0=n-2,n-1$
follows from Theorem 4.17, Proposition 6.5, Proposition 6.7, Proposition 6.10 and Proposition 7.1.
$m_0=n-2,n-1$
follows from Theorem 4.17, Proposition 6.5, Proposition 6.7, Proposition 6.10 and Proposition 7.1.
Assume that
![]() $n=5$
. If
$n=5$
. If
![]() $m_0=3$
, then
$m_0=3$
, then
![]() $\omega _1+\omega _3+\omega _4+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
unless
$\omega _1+\omega _3+\omega _4+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
unless
![]() $\mu =\omega _{3},2\omega _4,\omega _1+\omega _2$
or
$\mu =\omega _{3},2\omega _4,\omega _1+\omega _2$
or
![]() $3\omega _1$
. If
$3\omega _1$
. If
![]() $m_0=4$
, then
$m_0=4$
, then
![]() $2\omega _2+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
unless
$2\omega _2+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
unless
![]() $\mu =\omega _{4},\omega _1+\omega _{3}$
or
$\mu =\omega _{4},\omega _1+\omega _{3}$
or
![]() $\omega _1+2\omega _{4}$
. Set
$\omega _1+2\omega _{4}$
. Set
![]() $y_5=(1\ 5\ 3)(2\ 4)$
. Then it is easy to check that
$y_5=(1\ 5\ 3)(2\ 4)$
. Then it is easy to check that
![]() $\varpi ^{\omega _1+\omega _3+\omega _4} y_5\in {^S\mathrm {Adm}}(\omega _1+\omega _3+\omega _4)$
and
$\varpi ^{\omega _1+\omega _3+\omega _4} y_5\in {^S\mathrm {Adm}}(\omega _1+\omega _3+\omega _4)$
and
![]() $X_{\varpi ^{\omega _1+\omega _3+\omega _4} y_5}(\tau ^8)\neq \emptyset $
. Assume that
$X_{\varpi ^{\omega _1+\omega _3+\omega _4} y_5}(\tau ^8)\neq \emptyset $
. Assume that
![]() $n=4$
. If
$n=4$
. If
![]() $m_0=3$
, then
$m_0=3$
, then
![]() $2\omega _2+\omega _3+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
unless
$2\omega _2+\omega _3+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
unless
![]() $\mu =\omega _{3},\omega _1+\omega _2,\omega _1+2\omega _3$
or
$\mu =\omega _{3},\omega _1+\omega _2,\omega _1+2\omega _3$
or
![]() $3\omega _1$
. Set
$3\omega _1$
. Set
![]() $y_4=(1\ 3)(2\ 4)$
. Then it is easy to check that
$y_4=(1\ 3)(2\ 4)$
. Then it is easy to check that
![]() $\varpi ^{2\omega _2+\omega _3} y_4\in {^S\mathrm {Adm}}(2\omega _2+\omega _3)$
and
$\varpi ^{2\omega _2+\omega _3} y_4\in {^S\mathrm {Adm}}(2\omega _2+\omega _3)$
and
![]() $X_{\varpi ^{2\omega _2+\omega _3} y_4}(\tau ^7)\neq \emptyset $
. Assume that
$X_{\varpi ^{2\omega _2+\omega _3} y_4}(\tau ^7)\neq \emptyset $
. Assume that
![]() $n=3$
. If
$n=3$
. If
![]() $m_0=2$
, then
$m_0=2$
, then
![]() $2\omega _1+3\omega _2+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
unless
$2\omega _1+3\omega _2+\lfloor \frac {m}{n} \rfloor \omega _n\preceq \mu $
unless
![]() $\mu =\omega _{2},2\omega _1,\omega _1+2\omega _2,3\omega _1+\omega _2$
or
$\mu =\omega _{2},2\omega _1,\omega _1+2\omega _2,3\omega _1+\omega _2$
or
![]() $4\omega _2$
. Set
$4\omega _2$
. Set
![]() $y_3=(1\ 3)$
. Then it is easy to check that
$y_3=(1\ 3)$
. Then it is easy to check that
![]() $\varpi ^{2\omega _1+3\omega _2} y_3\in {^S\mathrm {Adm}}(2\omega _1+3\omega _2)$
and
$\varpi ^{2\omega _1+3\omega _2} y_3\in {^S\mathrm {Adm}}(2\omega _1+3\omega _2)$
and
![]() $X_{\varpi ^{2\omega _1+3\omega _2} y_3}(\tau ^8)\neq \emptyset $
. Thus, the equivalence of (i), (ii) and (iii) for
$X_{\varpi ^{2\omega _1+3\omega _2} y_3}(\tau ^8)\neq \emptyset $
. Thus, the equivalence of (i), (ii) and (iii) for
![]() $n=2,3,4,5$
also follows from Theorem 4.17, Proposition 6.5, Proposition 6.10 and Proposition 7.1. The case for
$n=2,3,4,5$
also follows from Theorem 4.17, Proposition 6.5, Proposition 6.10 and Proposition 7.1. The case for
![]() $n=1$
is trivially true.
$n=1$
is trivially true.
Assume that
![]() $\mu $
satisfies one of the conditions in the theorem, which is equivalent to each other as we have just proved. Except the cases where
$\mu $
satisfies one of the conditions in the theorem, which is equivalent to each other as we have just proved. Except the cases where
![]() $\mu $
or
$\mu $
or
![]() $\mu ^*$
is
$\mu ^*$
is
![]() $\omega _1+\omega _{n-2}\ (n\geq 4)$
or
$\omega _1+\omega _{n-2}\ (n\geq 4)$
or
![]() $\omega _1+\omega _2\ (n=5)$
, it follows from [Reference Viehmann43, Theorem 5.3] and Proposition 7.1 that each
$\omega _1+\omega _2\ (n=5)$
, it follows from [Reference Viehmann43, Theorem 5.3] and Proposition 7.1 that each
![]() $X_{\mu }^\lambda (b)(\neq \emptyset )$
is universally homeomorphic to an affine space. Here we will treat the case
$X_{\mu }^\lambda (b)(\neq \emptyset )$
is universally homeomorphic to an affine space. Here we will treat the case
![]() $\mu =\omega _1+\omega _{n-2}$
. The proof for
$\mu =\omega _1+\omega _{n-2}$
. The proof for
![]() $\mu =\omega _1+\omega _2$
is similar.
$\mu =\omega _1+\omega _2$
is similar.
Set
![]() $\mu =\omega _1+\omega _{n-2}$
and
$\mu =\omega _1+\omega _{n-2}$
and
![]() $\mu _{\bullet }=(\mu _1,\mu _2)=(\omega _1,\omega _{n-2})$
. By [Reference Nie32, Theorem 1.5] and the Cartesian square right after it,
$\mu _{\bullet }=(\mu _1,\mu _2)=(\omega _1,\omega _{n-2})$
. By [Reference Nie32, Theorem 1.5] and the Cartesian square right after it,
![]() $\operatorname {\mathrm {pr}}$
induces a bijection between
$\operatorname {\mathrm {pr}}$
induces a bijection between
![]() $\operatorname {\mathrm {pr}}^{-1}(X_\mu (b))(\subseteq X_{\mu _{\bullet }}(b_{{\bullet }}))$
and
$\operatorname {\mathrm {pr}}^{-1}(X_\mu (b))(\subseteq X_{\mu _{\bullet }}(b_{{\bullet }}))$
and
![]() $X_\mu (b)$
(cf. [Reference Shimada40, Lemma 3.11]). Since
$X_\mu (b)$
(cf. [Reference Shimada40, Lemma 3.11]). Since
![]() $\operatorname {\mathrm {pr}}$
is proper, it induces a universally homeomorphism onto its image. Thus by Theorem 3.12, it suffices to show that for any fixed
$\operatorname {\mathrm {pr}}$
is proper, it induces a universally homeomorphism onto its image. Thus by Theorem 3.12, it suffices to show that for any fixed
![]() $1\le j\le n-2$
and
$1\le j\le n-2$
and
![]() $[\lambda ]\in \mathbb A_\mu ^j$
, there exists a unique
$[\lambda ]\in \mathbb A_\mu ^j$
, there exists a unique
![]() $\lambda _{\bullet }=(\lambda _1,\lambda _2)\in \mathcal A_{\mu _{\bullet }}^j$
such that
$\lambda _{\bullet }=(\lambda _1,\lambda _2)\in \mathcal A_{\mu _{\bullet }}^j$
such that
![]() $\lambda _1=\lambda $
. If
$\lambda _1=\lambda $
. If
![]() $\lambda _{\bullet }\in \mathcal A_{\mu _{\bullet }}^j$
, then by [Reference Nie32, Proposition 2.9], we have
$\lambda _{\bullet }\in \mathcal A_{\mu _{\bullet }}^j$
, then by [Reference Nie32, Proposition 2.9], we have
By Lemma 5.3, we may assume that
![]() $[\lambda ]\in \mathbb A_\mu ^j$
has one of the following forms:
$[\lambda ]\in \mathbb A_\mu ^j$
has one of the following forms:
-
(1)
 $\lambda =(1,\ldots ,1,0,\ldots ,0,-1,\ldots ,-1,0,\ldots ,0)$
,
$\lambda =(1,\ldots ,1,0,\ldots ,0,-1,\ldots ,-1,0,\ldots ,0)$
, -
(2)
 $\lambda =(0,\ldots ,0,1,\ldots ,1,0,\ldots ,0,-1,\ldots ,-1)$
,
$\lambda =(0,\ldots ,0,1,\ldots ,1,0,\ldots ,0,-1,\ldots ,-1)$
, -
(3)
 $\lambda =(1,\ldots , 1,0,\ldots ,0,-1,\ldots ,-1)$
.
$\lambda =(1,\ldots , 1,0,\ldots ,0,-1,\ldots ,-1)$
.
Here the numbers of
![]() $1$
and
$1$
and
![]() $-1$
are equal. In the case (1) (resp. (2)), let
$-1$
are equal. In the case (1) (resp. (2)), let
![]() $i=\max \{i'\mid \lambda (i')=-1\}$
(resp.
$i=\max \{i'\mid \lambda (i')=-1\}$
(resp.
![]() $\min \{i'\mid \lambda (i')=1\}$
). Then
$\min \{i'\mid \lambda (i')=1\}$
). Then
![]() $(\lambda _2-\lambda )(i)=\lambda _2(i)+1$
and
$(\lambda _2-\lambda )(i)=\lambda _2(i)+1$
and
![]() $(b\lambda -\lambda _2)(i)=1-\lambda _2(i)$
(resp.
$(b\lambda -\lambda _2)(i)=1-\lambda _2(i)$
(resp.
![]() $(\lambda _2-\lambda )(i-1)=\lambda _2(i-1)$
and
$(\lambda _2-\lambda )(i-1)=\lambda _2(i-1)$
and
![]() $(b\lambda -\lambda _2)(i-1)=2-\lambda _2(i-1)$
). So if
$(b\lambda -\lambda _2)(i-1)=2-\lambda _2(i-1)$
). So if
![]() $\lambda _2-\lambda \in W_0\omega _1$
and
$\lambda _2-\lambda \in W_0\omega _1$
and
![]() $b\lambda -\lambda _2\in W_0\omega _{n-2}$
, then
$b\lambda -\lambda _2\in W_0\omega _{n-2}$
, then
![]() $\lambda _2(i)=0$
(resp.
$\lambda _2(i)=0$
(resp.
![]() $\lambda _2(i-1)=1$
). Hence, the i-th (resp.
$\lambda _2(i-1)=1$
). Hence, the i-th (resp.
![]() $(i-1)$
-th) entry of
$(i-1)$
-th) entry of
![]() $\lambda _2-\lambda $
is equal to
$\lambda _2-\lambda $
is equal to
![]() $1$
, and other entries are equal to
$1$
, and other entries are equal to
![]() $0$
. So
$0$
. So
![]() $\lambda _2$
is uniquely determined by
$\lambda _2$
is uniquely determined by
![]() $\lambda $
. In the case (3), we have
$\lambda $
. In the case (3), we have
![]() $(\lambda _2-\lambda )(n)=\lambda _2(n)+1$
and
$(\lambda _2-\lambda )(n)=\lambda _2(n)+1$
and
![]() $(b\lambda -\lambda _2)(n)=1-\lambda _2(n)$
. So if
$(b\lambda -\lambda _2)(n)=1-\lambda _2(n)$
. So if
![]() $\lambda _2-\lambda \in W_0\omega _1$
and
$\lambda _2-\lambda \in W_0\omega _1$
and
![]() $b\lambda -\lambda _2\in W_0\omega _{n-2}$
, then
$b\lambda -\lambda _2\in W_0\omega _{n-2}$
, then
![]() $\lambda _2(n)=0$
. So
$\lambda _2(n)=0$
. So
![]() $\lambda _2$
is also uniquely determined by
$\lambda _2$
is also uniquely determined by
![]() $\lambda $
.
$\lambda $
.
Other statements follow from the results (and proofs) in Section 5 and Section 6.
Acknowledgment
The author is grateful to his advisor Yoichi Mieda for his constant support and encouragement.