Article contents
Distance Sets of Urysohn Metric Spaces
Published online by Cambridge University Press: 20 November 2018
Abstract
A metric space 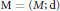 $\text{M=}\left( M;\text{d} \right)$ is homogeneous if for every isometry
$\text{M=}\left( M;\text{d} \right)$ is homogeneous if for every isometry 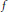 $f$ of a finite subspace of
$f$ of a finite subspace of 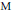 $\text{M}$ to a subspace of
$\text{M}$ to a subspace of 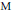 $\text{M}$ there exists an isometry of
$\text{M}$ there exists an isometry of 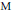 $\text{M}$ onto
$\text{M}$ onto 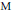 $\text{M}$ extending
$\text{M}$ extending 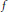 $f$ . The space
$f$ . The space 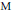 $\text{M}$ is universal if it isometrically embeds every finite metric space
$\text{M}$ is universal if it isometrically embeds every finite metric space  $\text{F}$ with
$\text{F}$ with 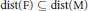 $\text{dist}\left( \text{F} \right)\subseteq \text{dist}\left( \text{M} \right)$ (with
$\text{dist}\left( \text{F} \right)\subseteq \text{dist}\left( \text{M} \right)$ (with 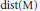 $\text{dist}\left( \text{M} \right)$ being the set of distances between points in
$\text{dist}\left( \text{M} \right)$ being the set of distances between points in 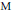 $\text{M}$ ).
$\text{M}$ ).
A metric space 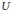 $U$ is a Urysohn metric space if it is homogeneous, universal, separable, and complete. (We deduce as a corollary that a Urysohn metric space
$U$ is a Urysohn metric space if it is homogeneous, universal, separable, and complete. (We deduce as a corollary that a Urysohn metric space 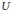 $U$ isometrically embeds every separable metric space
$U$ isometrically embeds every separable metric space 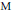 $\text{M}$ with
$\text{M}$ with 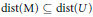 $\text{dist}\left( \text{M} \right)\subseteq \text{dist}\left( U \right)$ .)
$\text{dist}\left( \text{M} \right)\subseteq \text{dist}\left( U \right)$ .)
The main results are: (1) A characterization of the sets 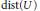 $\text{dist}\left( U \right)$ for Urysohn metric spaces
$\text{dist}\left( U \right)$ for Urysohn metric spaces 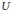 $U$ . (2) If
$U$ . (2) If 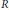 $R$ is the distance set of a Urysohn metric space and
$R$ is the distance set of a Urysohn metric space and 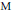 $\text{M}$ and
$\text{M}$ and 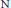 $\text{N}$ are two metric spaces, of any cardinality with distances in
$\text{N}$ are two metric spaces, of any cardinality with distances in 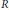 $R$ , then they amalgamate disjointly to a metric space with distances in
$R$ , then they amalgamate disjointly to a metric space with distances in 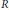 $R$ . (3) The completion of every homogeneous, universal, separable metric space
$R$ . (3) The completion of every homogeneous, universal, separable metric space 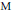 $\text{M}$ is homogeneous.
$\text{M}$ is homogeneous.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013
References
- 14
- Cited by

