Published online by Cambridge University Press: 20 November 2018
We construct covering maps from infinite blowups of the  $n$-dimensional Sierpinski gasket
$n$-dimensional Sierpinski gasket 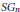 $S{{G}_{n}}$ to certain compact fractafolds based on
$S{{G}_{n}}$ to certain compact fractafolds based on 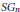 $S{{G}_{n}}$. These maps are fractal analogs of the usual covering maps fromthe line to the circle. The construction extends work of the second author in the case
$S{{G}_{n}}$. These maps are fractal analogs of the usual covering maps fromthe line to the circle. The construction extends work of the second author in the case 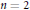 $n=2$, but a differentmethod of proof is needed, which amounts to solving a Sudoku-type puzzle. We can use the covering maps to define the notion of periodic function on the blowups. We give a characterization of these periodic functions and describe the analog of Fourier series expansions. We study covering maps onto quotient fractalfolds. Finally, we show that such covering maps fail to exist for many other highly symmetric fractals.
$n=2$, but a differentmethod of proof is needed, which amounts to solving a Sudoku-type puzzle. We can use the covering maps to define the notion of periodic function on the blowups. We give a characterization of these periodic functions and describe the analog of Fourier series expansions. We study covering maps onto quotient fractalfolds. Finally, we show that such covering maps fail to exist for many other highly symmetric fractals.