Hostname: page-component-7dd5485656-kp629 Total loading time: 0 Render date: 2025-10-31T05:00:29.212Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounding Selmer Groups for the Rankin–Selberg Convolution of Coleman Families

Part of: Arithmetic algebraic geometry Discontinuous groups and automorphic forms Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  17 July 2020

Andrew Graham ,
Daniel R. Gulotta  and
Yujie Xu
Andrew Graham*
Affiliation:
Department of Mathematics, South Kensington Campus, Imperial College London, London SW7 2AZ, UK
Daniel R. Gulotta
Affiliation:
Mathematical Institute, University of Oxford, Oxford OX2 6GG, UK e-mail: Daniel.Gulotta@maths.ox.ac.uk
Yujie Xu
Affiliation:
Department of Mathematics, Harvard University, 1 Oxford Street, Cambridge, MA 02138 e-mail: yujiex@math.harvard.edu
*
e-mail: a.graham17@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Let f and g be two cuspidal modular forms and let 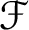${\mathcal {F}}$ be a Coleman family passing through f, defined over an open affinoid subdomain V of weight space 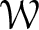$\mathcal {W}$. Using ideas of Pottharst, under certain hypotheses on f and 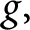$g,$ we construct a coherent sheaf over $V \times \mathcal {W}$ that interpolates the Bloch–Kato Selmer group of the Rankin–Selberg convolution of two modular forms in the critical range (i.e, the range where the p-adic L-function 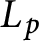$L_p$ interpolates critical values of the global L-function). We show that the support of this sheaf is contained in the vanishing locus of 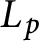$L_p$.

Keywords

Euler systemsSelmer complexesColeman familiesp-adic L-functionsGalois representations

MSC classification

Primary: 11F67: Special values of automorphic $L$-series, periods of modular forms, cohomology, modular symbols
Secondary: 11F85: $p$-adic theory, local fields 11G40: $L$-functions of varieties over global fields; Birch-Swinnerton-Dyer conjecture 14G35: Modular and Shimura varieties

Information

Type
Article
Information
Canadian Journal of Mathematics , Volume 73 , Issue 3 , June 2021 , pp. 805 - 853
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The Winter School was supported by NSF grant DMS-1504537 and by the Clay Mathematics Institute. AG was supported by the Engineering and Physical Sciences Research Council [EP/L015234/1], the EPSRC Centre for Doctoral Training in Geometry and Number Theory (The London School of Geometry and Number Theory), University College London and Imperial College London. DG was supported in part by Royal Society grant RP∖EA∖180020. YX was supported by Harvard University scholarships.

References

Andreatta, F. and Iovita, A., Triple product p-adic L-functions associated to finite slope p-adic families of modular forms, with an appendix by Eric Urban. arXiv:1708.02785 Google Scholar
Bellaïche, J., Critical $p$ -adic $L$ -functions. Invent. Math. 189(2012), no. 1, 1–60. https://doi.org/10.1007/s00222-011-0358-z CrossRefGoogle Scholar
Berger, L. and Colmez, P., Familles de représentations de de Rham et monodromie p-adique. Représentations p-adiques de groupes p-adiques I: Représentations galoisiennes et (φ,Γ)-modules, vol. 319, Astérisque, 2008, pp. 303–337.Google Scholar
Berger, L., Représentations $p$ -adiques et équations différentielles. Invent. Math. 148(2002), no. 2, 219–284. https://doi.org/10.1007/s002220100202 CrossRefGoogle Scholar
Berger, L., Bloch and Kato’s exponential map: three explicit formulas. Doc. Math (2003), Extra Vol., 99–129. http://eudml.org/doc/124694 Google Scholar
Coleman, R. F., Classical and overconvergent modular forms. Invent. Math 124(1996), no. 1-3, 215–241.CrossRefGoogle Scholar
Colmez, P., Représentations triangulines de dimension 2. Astérisque (2008), no. 319, 213–258.Google Scholar
Colmez, P., Fonctions d’une variable $p$ -adique. Astérisque 330(2010), 13–59. MR 2642404Google Scholar
Jannsen, U., Continuous étale cohomology. Math. Ann. 280(1988), no. 2, 207–245. https://doi.org/10.1007/BF01456052 CrossRefGoogle Scholar
Kedlaya, K. S. and Liu, R., On families of $(\varphi, \varGamma )$ -modules. Algebra. Number Theory 4(2010), no. 7, 943–967. https://doi.org/10.2140/ant.2010.4.943 CrossRefGoogle Scholar
Kedlaya, K. S., Pottharst, J., and Xiao, L., Cohomology of arithmetic families of $(\varphi, \varGamma )$ -modules. J. Amer. Math. Soc. 27(2014), no. 4, 1043–1115. https://doi.org/10.1090/S0894-0347-2014-00794-3 CrossRefGoogle Scholar
Kings, G., On $p$ -adic interpolation of motivic Eisenstein classes. Elliptic curves, modular forms and Iwasawa theory, Springer Proc. Math. Stat, 188, Springer, Cham, 2016, pp. 335–371.Google Scholar
Kings, G., Loeffler, D., and Zerbes, S. Livia, Rankin–Eisenstein classes for modular forms. Amer. J. Math (2015), to appear. https://arxiv.org/abs/1501.03289 Google Scholar
Kings, G., Loeffler, D., and Zerbes, S. Livia, Rankin-Eisenstein classes and explicit reciprocity laws. Camb. J. Math. 5(2017), no. 1, 1–122. https://doi.org/10.4310/CJM.2017.v5.n1.a1MR 3230818CrossRefGoogle Scholar
Lang, S., Introduction to modular forms. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 222, Springer-Verlag, Berlin, 1995, with appendixes by D. Zagier and Walter Feit. Corrected reprint of the 1976 original.Google Scholar
Lei, A., Loeffler, D., and Zerbes, S., Coleman maps and the p-adic regulator. Algebra. Number Theory 5(2011), no. 8, 1095–1131. https://doi.org/10.2140/ant.2011.5.1095 CrossRefGoogle Scholar
Lei, A., Loeffler, D., and Zerbes, S. L., Euler systems for Rankin-Selberg convolutions of modular forms. Ann. of Math. (2) 180(2014), no. 2, 653–771. https://doi.org/10.4007/annals.2014.180.2.6 CrossRefGoogle Scholar
Liu, R., Cohomology and duality for $(\phi, \varGamma )$ -modules over the Robba ring. Int. Math. Res. Not. IMRN (2008), no. 3, Art. ID rnm150. https://doi.org/10.1093/imrn/rnm150 Google Scholar
Liu, R., Triangulation of refined families. Comment. Math. Helv. 90(2015), no. 4, 831–904. https://doi.org/10.4171/CMH/372 CrossRefGoogle Scholar
Loeffler, D., Images of adelic Galois representations for modular forms. Glasg. Math. J. 59(2017), no. 1, 11–25. https://doi.org/10.1017/s0017089516000367 CrossRefGoogle Scholar
Loeffler, D., A Note on p-adic Rankin–Selberg L-functions. Canad. Math. Bull 61 (2018), no. 3, 608–621. https://doi.org/10.4153/CMB-2017-047-9 CrossRefGoogle Scholar
Loeffler, D. and Weinstein, J., On the computation of local components of a newform. Math. Comp. 81(2012), no. 278, 1179–1200. https://doi.org/10.1090/s0025-5718-2011-02530-5 CrossRefGoogle Scholar
Loeffler, D. and Zerbes, S. L., Rankin-Eisenstein classes in Coleman families. Res. Math. Sci. 3(2016), Art. ID 29. https://doi.org/10.1186/s40687-016-0077-6 CrossRefGoogle Scholar
Nakamura, K., Iwasawa theory of de Rham $(\varphi, \varGamma )$ -modules over the Robba ring. J. Inst. Math. Jussieu 13(2014), no. 1, 65–118. https://doi.org/10.1017/S1474748013000078 CrossRefGoogle Scholar
Nekovář, J., Selmer complexes. Astérisque (2006), no. 310, viii+559.Google Scholar
Perrin-Riou, B., $p$ -adic $L$ -functions and $p$ -adic representations. SMF/AMS Texts and Monographs, vol. 3, American Mathematical Society, Providence, RI; Société Mathématique de France, Paris, 2000, Translated from the 1995 French original by Leila Schneps and revised by the author.Google Scholar
Pottharst, J., Cyclotomic Iwasawa theory of motives. Preprint, 2012.Google Scholar
Pottharst, J., Analytic families of finite-slope Selmer groups. Algebra. Number Theory 7(2013), no. 7, 1571–1612. https://doi.org/10.2140/ant.2013.7.1571 CrossRefGoogle Scholar
Rubin, K., Euler systems. Ann. of Math., 147, Princeton University Press, Princeton, NJ, 2000, https://doi.org/10.1515/9781400865208 Google Scholar
Urban, E., Nearly overconvergent modular forms. Iwasawa Theory 2012 (Berlin, Heidelberg), Springer Berlin Heidelberg, 2014, pp. 401–441.Google Scholar