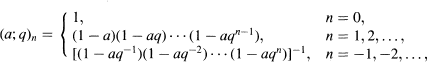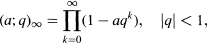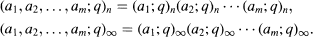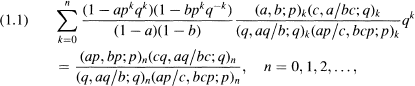Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zeilberger, Doron
1990.
A holonomic systems approach to special functions identities.
Journal of Computational and Applied Mathematics,
Vol. 32,
Issue. 3,
p.
321.
Foata, Dominique
and
Zeilberger, Doron
1991.
Multibasic Eulerian polynomials.
Transactions of the American Mathematical Society,
Vol. 328,
Issue. 2,
p.
843.
Ismail, Mourad E. H.
Takeuchi, Yu
and
Zhang, Ruiming
1993.
Pages from the computer files of R. William Gosper.
Proceedings of the American Mathematical Society,
Vol. 119,
Issue. 3,
p.
747.
Krattenthaler, C.
1996.
A new matrix inverse.
Proceedings of the American Mathematical Society,
Vol. 124,
Issue. 1,
p.
47.
Bhatnagar, Gaurav
and
Milne, Stephen C.
1997.
Generalized Bibasic Hypergeometric Series and TheirU(n) Extensions.
Advances in Mathematics,
Vol. 131,
Issue. 1,
p.
188.
Schlosser, Michael
1997.
Multidimensional Matrix Inversions and Ar and Dr Basic Hypergeometric Series.
The Ramanujan Journal,
Vol. 1,
Issue. 3,
p.
243.
Krattenthaler, Christian
and
Schlosser, Michael
1999.
A new multidimensional matrix inverse with applications to multiple q-series.
Discrete Mathematics,
Vol. 204,
Issue. 1-3,
p.
249.
Subbarao, M.V.
and
Verma, A.
1999.
Some summations of q-series by telescoping.
Pacific Journal of Mathematics,
Vol. 191,
Issue. 1,
p.
173.
Schlosser, Michael
1999.
Some New Applications of Matrix Inversions in A
r
.
The Ramanujan Journal,
Vol. 3,
Issue. 4,
p.
405.
Ciucu, M.
Eisenkölbl, T.
Krattenthaler, C.
and
Zare, D.
2001.
Enumeration of Lozenge Tilings of Hexagons with a Central Triangular Hole.
Journal of Combinatorial Theory, Series A,
Vol. 95,
Issue. 2,
p.
251.
Warnaar, S. O.
2002.
Summation and transformation formulas for elliptic hypergeometric series.
Constructive Approximation,
Vol. 18,
Issue. 4,
p.
479.
Berkovich, Alexander
and
Garvan, Frank G.
2002.
Some Observations on Dyson's New Symmetries of Partitions.
Journal of Combinatorial Theory, Series A,
Vol. 100,
Issue. 1,
p.
61.
Berkovich, Alexander
and
Warnaar, S.
2004.
Positivity preserving transformations for 𝑞-binomial coefficients.
Transactions of the American Mathematical Society,
Vol. 357,
Issue. 6,
p.
2291.
Stanton, D.
2005.
Theory and Applications of Special Functions.
Vol. 13,
Issue. ,
p.
401.
Ma, Xinrong
2007.
The (f,g)-inversion formula and its applications: The (f,g)-summation formula.
Advances in Applied Mathematics,
Vol. 38,
Issue. 2,
p.
227.
Chu, Wenchang
and
Wang, Xiaoyuan
2008.
Abel’s lemma on summation by parts and terminating q-series identities.
Numerical Algorithms,
Vol. 49,
Issue. 1-4,
p.
105.
Zhang, Yusen
and
Wang, Tianming
2008.
Some Applications of Gasper's Bibasic Summation.
Rocky Mountain Journal of Mathematics,
Vol. 38,
Issue. 2,
Chu, Wenchang
and
Wang, Xiaoxia
2009.
The modified Abel lemma on summation by parts and terminating hypergeometric series identities.
Integral Transforms and Special Functions,
Vol. 20,
Issue. 2,
p.
93.
Chu, WenChang
and
Wang, ChenYing
2009.
Abel’s lemma on summation by parts and partial q-series transformations.
Science in China Series A: Mathematics,
Vol. 52,
Issue. 4,
p.
720.
Chu, Wenchang
and
Jia, Cangzhi
2013.
Quartic theta hypergeometric series.
The Ramanujan Journal,
Vol. 32,
Issue. 1,
p.
23.