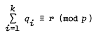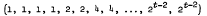Contents
Abstracts of Australasian PhD theses
Variability of Room squares
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 479-480
-
- Article
-
- You have access
- Export citation
Research Article
The intersection of a continuum of open dense sets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 267-272
-
- Article
-
- You have access
- Export citation
A result on tournaments with an application to counting
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 273-278
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
A geometry with spinor connection as a model for space, time and matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 151-152
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 16 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
Estimation for vector linear time series models
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 153-154
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 16 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Stratifications of equivariant varieties
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 279-295
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
Models of well-orderings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 155-157
-
- Article
-
- You have access
- Export citation
Research Article
Using product designs to construct orthogonal designs
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 297-305
-
- Article
-
- You have access
- Export citation
The automorphism group of a scattered set can be non-commutative
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 306
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
Topological measure theory, with applications to probability
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 159-160
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 16 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
A study of certain modular representations
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 307-309
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 16 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD theses
A non-linear boundary value problem arising in the theory of thermal explosions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 311-312
-
- Article
-
- You have access
- Export citation
Crosstalk between optical waveguides with applications to visual photoreceptors
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 313-314
-
- Article
-
- You have access
- Export citation
A singular perturbation approach to some problems in chemical kinetics
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 315-316
-
- Article
-
- You have access
- Export citation
Corrigenda
Groups of automorphisms of linearly ordered sets: Corrigenda
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 317-318
-
- Article
-
- You have access
- Export citation
Transformations on tensor products and the torsionless property in abelian groups: Corrigendum
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 319
-
- Article
-
- You have access
- Export citation