Research Article
Semilinear problems on the half space with a hole
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 235-247
-
- Article
-
- You have access
- Export citation
Unicity theorems for meromorphic or entire functions III
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 71-82
-
- Article
-
- You have access
- Export citation
Single identities for Mendelsohn and Steiner 3-quasigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 419-424
-
- Article
-
- You have access
- Export citation
Modules arising from some relative injectives
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 249-260
-
- Article
-
- You have access
- Export citation
Essential covers and complements of radicals
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 261-266
-
- Article
-
- You have access
- Export citation
Commensurability and elementary equivalence of polycyclic groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 425-439
-
- Article
-
- You have access
- Export citation
Non-coprime quadratic systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 83-90
-
- Article
-
- You have access
- Export citation
Critical algebras and the Frattini congruence, II
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 91-100
-
- Article
-
- You have access
- Export citation
On finite products of totally permutable groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 441-445
-
- Article
-
- You have access
- Export citation
Set covering number for a finite set
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 267-269
-
- Article
-
- You have access
- Export citation
A note on strong geometric isolation in 3-orbitfolds
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 271-280
-
- Article
-
- You have access
- Export citation
Almost fixed point and best approximations theorems in H-spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 447-454
-
- Article
-
- You have access
- Export citation
On the self-length of two-dimensional Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 101-107
-
- Article
-
- You have access
- Export citation
Diophantine equations of Erdös-Moser type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 281-292
-
- Article
-
- You have access
- Export citation
Differential inclusions and abstract control problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 109-122
-
- Article
-
- You have access
- Export citation
A characterisation of reflexive modules
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 455-458
-
- Article
-
- You have access
- Export citation
A note on frame starters
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 293-297
-
- Article
-
- You have access
- Export citation
M-harmonic functions with M-harmonic square
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 123-129
-
- Article
-
- You have access
- Export citation
Remarks on bounded solutions of linear systems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 459-467
-
- Article
-
- You have access
- Export citation
Width-diameter relations for planar convex sets with lattice point constraints
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 469-478
-
- Article
-
- You have access
- Export citation

 of the equation −Δ
of the equation −Δ -residual, where
-residual, where  -projectors and
-projectors and 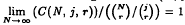 was proved by Rödl, no nontrivial upper bound for
was proved by Rödl, no nontrivial upper bound for 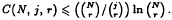
 . For
. For 
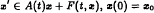 in Banach spaces. Here {
in Banach spaces. Here {