Contents
Research Article
Local analytic structure in certain commutative topological algebras
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-167
-
- Article
-
- You have access
- Export citation
Projective groups in varieties
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 169-175
-
- Article
-
- You have access
- Export citation
Profinite posets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 177-183
-
- Article
-
- You have access
- Export citation
Inequalities related to those of Hausdorff-Young
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 185-210
-
- Article
-
- You have access
- Export citation
On theorems of Thornton
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 211-212
-
- Article
-
- You have access
- Export citation
The Fitting length of a finite soluble group and the number of conjugacy classes of its maximal nilpotent subgroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 213-226
-
- Article
-
- You have access
- Export citation
Inductive and projective limits of smooth topological vector spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 227-240
-
- Article
-
- You have access
- Export citation
Extreme point properties of fixed-point sets
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 241-249
-
- Article
-
- You have access
- Export citation
A remark on Ribenboim's paper ‘On the extension of orders in ordered modules’
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 251-253
-
- Article
-
- You have access
- Export citation
On the maximal normal prime-nilpotent subgroup of a prime-solvable group
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 255-262
-
- Article
-
- You have access
- Export citation
Extension of multipliers by periodicity
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 263-285
-
- Article
-
- You have access
- Export citation
The subnormal structure of metanilpotent groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 287-306
-
- Article
-
- You have access
- Export citation
Functions of asymptotic expansions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 307-312
-
- Article
-
- You have access
- Export citation
A non-cyclic, locally free, free-by-cyclic group all of whose finite factor groups are cyclic
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 313-314
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian Ph.D. theses
Fixed points of semigroups in a Choquet simplex and compactlfication
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 315-316
-
- Article
-
- You have access
- Export citation
Simultaneous diophantine approximation
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 317-318
-
- Article
-
- You have access
- Export citation
Corrigendum
Some definitions of finiteness: Corrigenda
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 319
-
- Article
-
- You have access
- Export citation
Front matter
BAZ volume 6 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
BAZ volume 6 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
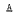 an algebra of formal power series over
an algebra of formal power series over  whose range contains polynomials is necessarily continuous provided the coordinate projections of
whose range contains polynomials is necessarily continuous provided the coordinate projections of