Published online by Cambridge University Press: 30 August 2018
We give two-sided estimates for positive solutions of the superlinear
elliptic problem 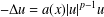 $-\unicode[STIX]{x1D6E5}u=a(x)|u|^{p-1}u$ with zero Dirichlet boundary condition in a bounded
Lipschitz domain. Our result improves the well-known a priori
$-\unicode[STIX]{x1D6E5}u=a(x)|u|^{p-1}u$ with zero Dirichlet boundary condition in a bounded
Lipschitz domain. Our result improves the well-known a priori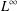 $L^{\infty }$-estimate and provides information about the boundary decay
rate of solutions.
$L^{\infty }$-estimate and provides information about the boundary decay
rate of solutions.
This work was supported in part by JSPS KAKENHI Grant Number JP18K03333.