Article contents
REFLEXIVE INDEX OF A FAMILY OF SUBSPACES
Published online by Cambridge University Press: 02 April 2014
Abstract
A definition of the reflexive index of a family of (closed) subspaces of a complex, separable Hilbert space 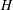 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}H$ is given, analogous to one given by D. Zhao for a family of subsets of a set. Following some observations, some examples are given, including: (a) a subspace lattice on
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}H$ is given, analogous to one given by D. Zhao for a family of subsets of a set. Following some observations, some examples are given, including: (a) a subspace lattice on 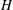 $H$ with precisely five nontrivial elements with infinite reflexive index; (b) a reflexive subspace lattice on
$H$ with precisely five nontrivial elements with infinite reflexive index; (b) a reflexive subspace lattice on 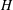 $H$ with infinite reflexive index; (c) for each positive integer
$H$ with infinite reflexive index; (c) for each positive integer  $n$ satisfying dim
$n$ satisfying dim 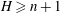 $H\ge n+1$, a reflexive subspace lattice on
$H\ge n+1$, a reflexive subspace lattice on 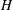 $H$ with reflexive index
$H$ with reflexive index  $n$. If
$n$. If 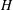 $H$ is infinite-dimensional and
$H$ is infinite-dimensional and 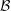 ${\mathcal{B}}$ is an atomic Boolean algebra subspace lattice on
${\mathcal{B}}$ is an atomic Boolean algebra subspace lattice on 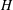 $H$ with
$H$ with  $n$ equidimensional atoms and with the property that the vector sum
$n$ equidimensional atoms and with the property that the vector sum 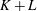 $K+L$ is closed, for every
$K+L$ is closed, for every 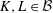 $K,L\in {\mathcal{B}}$, then
$K,L\in {\mathcal{B}}$, then 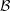 ${\mathcal{B}}$ has reflexive index at most
${\mathcal{B}}$ has reflexive index at most  $n$.
$n$.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © 2014 Australian Mathematical Publishing Association Inc.
References
- 2
- Cited by

