Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-25T21:19:23.200Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Riemann zeta-function I

Published online by Cambridge University Press:  17 April 2009

Masako Izumi  and
Shin-ichi Izumi
Masako Izumi
Affiliation:
Department of Mathematics, Institute of Advanced Studies, Australian National University, Canberra, ACT.
Shin-ichi Izumi
Affiliation:
Department of Mathematics, Institute of Advanced Studies, Australian National University, Canberra, ACT.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove an approximation formula for the Riemann zeta function. We show that a classical theorem:

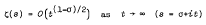
uniformly in the domain ½ ≤ σ < 1, is an immediate consequence of our approximation formula. Our method is real and free from complex analysis.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 15 , Issue 2 , October 1976 , pp. 161 - 211
Copyright
Copyright © Australian Mathematical Society 1976

References

[1]Edwards, H.M., Riemann's zeta function (Academic Press, New York, London, 1974).Google Scholar
[2]Hardy, G.H. and Littlewood, J.E., “The approximate functional equation in the theory of the zeta-function, with applications to the divisor-problems of Dirichlet and Piltz”, Proc. London Math. Soc. (2) 21 (1922), 39–74.Google Scholar
[3]Titchmarsh, E.G., The theory of the Riemann zeta-function (Clarendon Press, Oxford, 1951).Google Scholar